在傳統光學材料中,單光子之間的非線性相互作用弱到可以被忽略。這篇論文發現,一種冷而緻密的原子氣在單量子層面上可以是非線性的,表現出強的“光子對”吸收,而對單光子仍保持透明(即可被穿透)。該方法開啟了按單量子來控制光場、包括單光子開關及確定性(deterministic)量子邏輯的可能性。本文作者提出,該方法也有可能被延伸到其他材料體系,後者在它們可被耦合到光的各組分之間有強相互作用。
更深刻更科学前沿一点,就再多说一点点本博主的老本行,飞秒激光(femto-second laser)。飞秒激光就是一种非常短的光脉冲,这个光的队伍特别长,就是说对应的光波长(λi)很多,越多光波长加进去这个队伍,这个光脉冲时间就很有可能更短(量子测不准原理决定的)。现在同行都知道,把整个可见光都包括进去都已经很容易了,看起来就是白光,跟太阳光谱非常接近,也就是说,很容易展示出一个飞秒光脉冲,用牛顿的三角棱镜散开以后看到从深蓝到深红都有,技术上这一点都不麻烦(见上图右)。关键问题是,如果管理好这个光频率队伍前进中的整齐度问题,因为这个队伍太容易被拉长而变形得不像样,也就是说保持飞秒的传播很困难,顺便,光孤子通讯技术也在这个领域。顺便多说一句,日常照明的荧光灯的那个白光不是真正的白光,里面包含了太阳白光的几个很窄的波段,用以骗过人的眼睛而已
[PPT]第八讲
n例如,发射台不断向接受者发射脉冲信号,无论接受者是静止还是在运动,他接收到脉冲的个数是相同的。所以,相位是一个不变量,对不同的观察者不变。这可以通过洛伦兹变换来证明,但在牛顿力学中,根据伽利略变换与多普勒效应无法保证相位不变性。
n相位不变性是德布罗意发现的,它是研究电磁场的相对论效应乃至量子理论的基础。
在闵可夫斯基背景时空中,由局域惯性系的静电学定律就可以建立电动力学的理论体系,闵氏时空的间隔不变性自动导致光速不变与电磁学的洛伦兹协变性phymath999: qft white 相位不变性粒子参数E和pv 狭义相对论 ...
2015年5月1日 - qft white 相位不变性粒子参数E和pv 狭义相对论基本公理——所有保持平直的时空坐标变换需满足任意两个事件的时空间隔不变性。由于四动量 ...
phymath999: u單位向量, 利用u決定通過P0的直線參數方程式 ...
phymath999.blogspot.com/2013/07/u-up0us.html
2013年7月15日 - 沿 方向的導函數,其實就是對直線參數s的變化率. 第三章 純量與向量 ..... 把散射截面能譜曲綫上的尖峰看成是粒子,叫做共振態。共振態粒子的質量 ...
纳并加以发展。 〈 角动量量子化条件 - Course Hero
https://www.coursehero.com/.../%25E7%25BA%25B3%25... - 轉為繁體網頁
1 ) 就是说,若已知等式右边的粒子参数E 和p v ,便可由这组关系式求得该粒子所具有的波动特性。上面两组关系式的中间桥梁便是Planck 常数h , 形象地写出便是(单光子探测器编辑
中文名
单光子探测器
外文名
SPD
性 质
探测器
类 型
超低噪声器件
1军事方面的用途编辑
光子,是光的最小能量量子。单光子探测技术,是近些年刚刚起步的一种新式光电探测技术,其原理是利用新式光电效应,可对入射的单个光子进行计数,以实现对极微弱目标信号的探测。有关专家认为,单光子探测技术能将现有的机载光电探测距离从几十公里提高到几千公里,势必带来机载目标探测系统的革命,极大地改变未来空天战场的作战方式。
隐身飞机将无处“隐身”。F-22、B-2等飞机高超的隐身性能,几乎使现役雷达和光电探测系统变成“瞎子”。但单光子探测系统极高的探测灵敏度,即使对F-22、B-2这样的隐身飞机,作用距离也可达到几百到几千公里,可在极远距离上发现隐身飞机,使其“无处遁形”。
空战将从“中距”拉向“远距”。配装单光子探测系统的作战飞机,由于对空目标探测距离极远,将使空中作战从目前的中距进一步扩为远距。如:配挂单光子超远程空空导弹,火力攻击距离可达到几百到几千公里之外。空中战争将从传统的几十公里的超视距作战变为间隔几千公里的非接触战争。
“全球感知,全球打击”成为可能。利用空中平台或临近空间平台配装单光子探测系统,构建单光子探测网络,只需几部单光子探测系统就可实现对领空的全域覆盖。在此基础上用地面或空中远程导弹构建空中地面联合火力网,把单光子探测网络作为网络中心战的目标探测网络系统,可对任何位置(地面或空中)发射的导弹进行目标指引,有效攻击全球目标,实现“全球感知,全球打击”。
2光谱测量编辑
利用单光子探测技术,可极大提高光谱测量的灵敏度和精确性,灵敏度提高3-4个数量级,可实现对微量物质成分的光谱分析,使化学成分检测和安全检查等系统达到超高灵敏度。
3生物发光编辑
生物发光是一种微弱的准连续光子辐射现象。利用单光子探测技术能对生物发光进行有效探测,可用于分析生物体内特别体系的功能以及细胞的代谢或破坏过程,还能有效的推动现代医学对于脑功能和基因工程的研究。
4光纤传感编辑
光纤传感工作频带宽、动态范围大、适合遥测遥控、可低损耗传输,利用单光子探测技术可极大地提高光纤传感的灵敏度和监控长度,对输油管道和海底光缆的安全监控、大型建筑的火灾报警、海岸线或边境安全等领域具有重大意义
不是弦共振頻率的部分很快就會衰減,最後剩下的頻率才是傳到我們耳朵的聲音
http://highscope.ch.ntu.edu.tw/wordpress/?p=19239
現將一把完整的小提琴分解為2個獨立系統:拉弦系統和共振箱系統,如圖1(實際上 ... 電子小提琴由無共鳴箱的實木琴架、琴弦及提琴配件構成琴體,在琴弦下面裝配有 ...
相对速度,群速度相速度,快慢光,超光速,光孤子,飞秒阿秒
不是弦共振頻率的部分很快就會衰減,最後剩下的頻率才是傳到我們耳朵的聲音
http://highscope.ch.ntu.edu.tw/wordpress/?p=19239
聲音的共振–共鳴(Acoustic Resonance)
聲音的共振--共鳴(Acoustic Resonance)國立彰化高級中學物理科劉翠鵑老師/國立臺灣師範大學物理系蔡志申教授責任編輯
共鳴是指發聲體受到其固有頻率(或稱共振頻率)的外力驅動時,會比被其他頻率外力驅動時吸收更多能量。共鳴就是振動頻率在人聽覺範圍內(頻率是介於20Hz~20000Hz之間)的共振現象。一般而言,聲音的共振體會有一個以上的共振頻率,尤其頻率是最低頻整數倍(通常把這樣頻率的聲音稱為諧音)共振強度最強。亦即當一個含各種頻率的波動(例如:脈衝波、噪音等)傳至共振體,共振體會過濾掉除了共振頻以外的頻率。大多數的樂器在製造時,皆須考慮到共鳴的效應。透過共鳴箱的設計,可以使振動的空氣量增加,例如:小提琴或吉他的音箱。
弦樂器中,如:如琵琶,豎琴,吉他,鋼琴,小提琴等,弦在張緊的情況下也有所謂的共振頻,而且這些弦樂器的共振頻是由弦的質量、長度與弦張力決定的。產生第一共振頻(即最低頻,也稱基頻或基音)的波長恰為弦長的兩倍,至於其他更高共振頻(也稱泛音)的波長則是基頻波長的整數倍分之一。這些對應的共振頻與弦波波速有關,如(1)式 其中 L 是弦長(兩端固定的弦), N = 1,2,3…
其中 L 是弦長(兩端固定的弦), N = 1,2,3…
至於弦波或繩波波速 v 則與張力 T 和單位長度的質量 ρ 有關,如(2)式
則共振頻率 其中 M 是弦的總質量
其中 M 是弦的總質量
 張力愈大或弦長愈短可使共振頻率愈大。用手彈一下弦或用錘敲打產生一脈衝波在弦上傳播時,弦將會以各種頻率振動(脈衝波是由各種頻率的正弦波疊加而成的),但其中不是弦共振頻率的部分很快就會衰減,最後剩下的頻率才是傳到我們耳朵的聲音。此外,當某一弦發出聲音時可能會引發其他弦以其共振頻(基頻或更高頻)開始振動。例如:基頻440Hz的A弦振動時會引發基頻330Hz的E弦共振,因為兩弦同時有1320Hz的共振頻(A弦的第三諧音或第二泛音,E弦的第四諧音或第三泛音)。
張力愈大或弦長愈短可使共振頻率愈大。用手彈一下弦或用錘敲打產生一脈衝波在弦上傳播時,弦將會以各種頻率振動(脈衝波是由各種頻率的正弦波疊加而成的),但其中不是弦共振頻率的部分很快就會衰減,最後剩下的頻率才是傳到我們耳朵的聲音。此外,當某一弦發出聲音時可能會引發其他弦以其共振頻(基頻或更高頻)開始振動。例如:基頻440Hz的A弦振動時會引發基頻330Hz的E弦共振,因為兩弦同時有1320Hz的共振頻(A弦的第三諧音或第二泛音,E弦的第四諧音或第三泛音)。
至於空氣管的共鳴,則與管子的長度、形狀以及管子兩端開閉與否有關。將一端開一端閉的空氣管稱為閉管,兩端皆開的空氣管稱為開管。管樂器中空氣管形狀通常是錐狀或圓柱狀,例如:長笛是圓柱狀的開管,單簧管和銅管樂器則是圓柱狀的必管,至於薩克斯風、雙簧管及Bassoon管則是錐狀的閉管。
空氣柱的振動跟琴弦一樣是以諧頻共振。
對於圓柱狀開管的共振頻率 其中 N 為正整數(1,2,3…),如下圖(二)所示
其中 N 為正整數(1,2,3…),如下圖(二)所示
對應不同的駐波模式, L 代表空氣管的長度, v 代表空氣中的聲速(20℃ 的海平面聲速大約是 343m/s )
若要更準確的關係式,則應考慮管口的修正量(1860年H. von Helmholtz 詳盡地討論了管口修正的問題)
 其中 N 為奇數(1,3,5…),如下圖(三)所示
其中 N 為奇數(1,3,5…),如下圖(三)所示
這種管子只有奇數的共振頻,而且它的基頻大小是相同管長的開管基頻之半。若考慮管口的修正,圓柱狀閉管的共振頻率為

參考資料:1.維基百科--共鳴 http://en.wikipedia.org/wiki/Acoustic_resonance
圖片來源:
http://www.physics.umd.edu/lecdem/misc/phys102/PH102chap03.ppt
共鳴是指發聲體受到其固有頻率(或稱共振頻率)的外力驅動時,會比被其他頻率外力驅動時吸收更多能量。共鳴就是振動頻率在人聽覺範圍內(頻率是介於20Hz~20000Hz之間)的共振現象。一般而言,聲音的共振體會有一個以上的共振頻率,尤其頻率是最低頻整數倍(通常把這樣頻率的聲音稱為諧音)共振強度最強。亦即當一個含各種頻率的波動(例如:脈衝波、噪音等)傳至共振體,共振體會過濾掉除了共振頻以外的頻率。大多數的樂器在製造時,皆須考慮到共鳴的效應。透過共鳴箱的設計,可以使振動的空氣量增加,例如:小提琴或吉他的音箱。
弦樂器中,如:如琵琶,豎琴,吉他,鋼琴,小提琴等,弦在張緊的情況下也有所謂的共振頻,而且這些弦樂器的共振頻是由弦的質量、長度與弦張力決定的。產生第一共振頻(即最低頻,也稱基頻或基音)的波長恰為弦長的兩倍,至於其他更高共振頻(也稱泛音)的波長則是基頻波長的整數倍分之一。這些對應的共振頻與弦波波速有關,如(1)式
 其中 L 是弦長(兩端固定的弦), N = 1,2,3…
其中 L 是弦長(兩端固定的弦), N = 1,2,3…至於弦波或繩波波速 v 則與張力 T 和單位長度的質量 ρ 有關,如(2)式

則共振頻率
 其中 M 是弦的總質量
其中 M 是弦的總質量
至於空氣管的共鳴,則與管子的長度、形狀以及管子兩端開閉與否有關。將一端開一端閉的空氣管稱為閉管,兩端皆開的空氣管稱為開管。管樂器中空氣管形狀通常是錐狀或圓柱狀,例如:長笛是圓柱狀的開管,單簧管和銅管樂器則是圓柱狀的必管,至於薩克斯風、雙簧管及Bassoon管則是錐狀的閉管。
空氣柱的振動跟琴弦一樣是以諧頻共振。
對於圓柱狀開管的共振頻率
 其中 N 為正整數(1,2,3…),如下圖(二)所示
其中 N 為正整數(1,2,3…),如下圖(二)所示對應不同的駐波模式, L 代表空氣管的長度, v 代表空氣中的聲速(20℃ 的海平面聲速大約是 343m/s )
若要更準確的關係式,則應考慮管口的修正量(1860年H. von Helmholtz 詳盡地討論了管口修正的問題)
圓柱狀開管的共振頻率修正為  ,其中 d 代表共振管的內徑。
,其中 d 代表共振管的內徑。
此關係式說明了一個重要結論,空氣管開口端邊緣並非零聲壓,故聲波在開口端的反射位置不會恰好在管子的邊緣,而是由管邊緣向外延伸一小段距離的位置。當聲波傳到共振管的開口端時,其反射率略小於1。亦即開口端的聲阻抗不完全等於零,而是一個有限值(稱為輻射阻抗),且此阻抗與管徑、聲波波長及管口的樣式有關。

對於圓柱狀閉管的共振頻率  ,其中 d 代表共振管的內徑。
,其中 d 代表共振管的內徑。此關係式說明了一個重要結論,空氣管開口端邊緣並非零聲壓,故聲波在開口端的反射位置不會恰好在管子的邊緣,而是由管邊緣向外延伸一小段距離的位置。當聲波傳到共振管的開口端時,其反射率略小於1。亦即開口端的聲阻抗不完全等於零,而是一個有限值(稱為輻射阻抗),且此阻抗與管徑、聲波波長及管口的樣式有關。

 其中 N 為奇數(1,3,5…),如下圖(三)所示
其中 N 為奇數(1,3,5…),如下圖(三)所示這種管子只有奇數的共振頻,而且它的基頻大小是相同管長的開管基頻之半。若考慮管口的修正,圓柱狀閉管的共振頻率為


參考資料:1.維基百科--共鳴 http://en.wikipedia.org/wiki/Acoustic_resonance
圖片來源:
http://www.physics.umd.edu/lecdem/misc/phys102/PH102chap03.ppt
您或許對這些文章有興趣
電子小提琴與常規小提琴的無線載波傳輸演示
[PDF]一、樂器的發聲原理: (1)絃樂器:通過拉、彈、撥,擊的方法使 ...
(1)絃樂器:通過拉、彈、撥,擊的方法使弦振動而發聲,再借助共鳴箱使弦的聲音在. 共鳴箱中強迫共振而被放大。常見的絃樂器有小提琴、大提琴、吉他,二. 胡、琵琶 ...
w3.fhsh.tp.edu.tw/sub/subject04/handout/h1/4-4.pdf
There is 1 comment for this article
相对速度,群速度相速度,快慢光,超光速,光孤子,飞秒阿秒
一不小心,一道小学生的数学题在科学网上引发一场众人关注的血案(小红花)
据说别人问哪个诺依曼来着,诺依曼立刻回答100米,然后那人很赞叹的说“我本还以为你会用无穷级数来算”,诺依曼说“我就是用那个算的”。。。好像出自《读者》?

先是一篇鲍博主的《相对论---破解一道小学数学题 》,本来就是一个‘相对速度’的问题,被望文生意成爱因斯坦的‘相对论’,于是引来一批人围观,指指点点,岂不知,大多数人的指点都是错误的,因为思维上没有转弯,还不如队伍中的最后那位,跑到最前头就180度的急转弯。

然后来了一篇《补记》,的确,这个和这类问题不应该送给小学生去考虑,至少它用到了根号问题。合适的问题可以是一位博友说的,一位在行进的火车上跑前跑后的问题。
我开始注意到的时候,也就已经血流遍地了,就是程博主的《也谈“相对速度”》。
这个问题的原本就是那头无头的苍蝇来回飞的问题,地地道道的数学上的无穷级数问题:
程博主博文引用为:
(2) 关晴骁问题(见首篇[34])
两辆自行车A,B间隔100米相向而行,两车都是每秒走一米,他们出发那一刻,一苍蝇每秒2米的速度从A车直线往B车飞,飞到B车后转头又往A车飞,问两车相遇时,苍蝇飞了多少米?
这个无穷级数问题的超级简化,只取第一项,就是鲍博主提到的,继续引用如下,
鲍得海问题(见首篇[29]):一列队伍长M米,向前行驶,队伍中最后一个人,以较快的速度沿着同样的方向前进,当这个人走到队伍的最前头的时候,返回身来再往回走,一直走到队伍的最后,这时,整列队伍恰好向前行走了N米。提问:单独的这个人走了多少距离?
最后演化成为难倒小学生,大学生到一帮博主的问题,
一列队伍长一百米,向前行驶,队伍中最后一个人(二者均为匀速),以较快的速度沿着同样的方向前进,当这个人走到队伍的最前头的时候,返回身来再往回走,一直走到队伍的最后,这时,整列队伍恰好向前行走了100米。提问:单独的这个人走了多少路程?
这些问题的答案上面三篇博文中已经交待得很清楚了。但是,我觉得血流还远远不够,还需要继续大刀阔斧地往下砍,骨头需要劈开,看清楚里面的骨髓脑髓,自道是那白的红的一道露出来了。

关键核心问题是,一列队伍长M米,向前行驶,如果队伍中每一个人,以不同的速度沿着同样的方向前进,结果会怎样?
找到一个非常贴切的例子是,物理学中光学学科的群速度,相速度和相关的超光速,慢光速问题。
对于这个行进中的队伍,就是一个光脉冲,其中包括了很多光的频率,怎样一起向前传播的问题。这里每一个光的频率是vi,对应一个波长 λi。
相速度:是对个人来说的,队伍中每一个人的行进速度不同;就是说光脉冲中每个光频率(vi)的传播速度不同(因此每个光波的频率不相同),每个频率都有一个自己的相速度。
群速度:就是整个队伍的行进速度,光脉冲中许多不同频率的光波合成在一起在介质中传播的整体速度。不同频率波的振幅和相位不同,在介质中,相速度因此不同,故在不同的空间位置上的合成信号形状会发生变化。群速度是一个代表整体能量的传播速度。
关键一点是,队伍中每个成员的体力和身体素质不同,导致相速度不同,行进中会产成队伍的次序重组现象,有的开始靠前,过一段时间/距离以后就变得靠后,反之亦然,开始时刻靠后的,后来会变得靠前,也有可能更靠后,这样队伍会被缩短,或者拉长,特殊情况也就是理想状况下,各个成员身体素质和体力相同,则队伍形状不变。
相对应,光脉冲向前传播中的过程完全类似,因为介质(真空除外)都有一定的折射率n,对每个光波长(λi,频率vi))不同,称为 ni,导致不同光频率(vi)的传播速度(相速度)也不同。所以,光脉冲会被介质拉长,这是最普遍情况,甚至缩短,这是极少情况,甚至在特定情况下相对速度不变,叫做光孤子。缩短情况也是相对而言的,因为缩到最短之后再继续向前传播就是拉长了,这就相当于,开始的队伍前头落到了最后头,体力跟不上了,把队伍拉长了,甚至最后掉队了。
这里顺便把快光速(也叫超光速)和慢光速问题也就说明了,这两个术语就是指的是光的相速度相对于群速度问题。还可以比喻说,一列队伍缓慢进行,有队员脚步跳得很快但是实际上没有向前跑很快,极端情况是原地踏步走。也有队伍行进快,但是队员迈步较慢但是步伐很大的情况(完全跟得上队伍),这就是慢光速了,极端的例子是光速为零,这个领域每隔几年 媒体就会热炒,外行吃惊,内行则不以为然。
现在的光速大概是每秒30万公里,托爱因斯坦他老人家引入的这个假设的福,这个极限我不相信在宇宙中我们所处的这一块领地能够被打破。至于2011年的意大利的中微子超光速一说,这里的超光速是指群速度而不是相速度,刚出现的时候真正内行人中大家的直觉就是乌龙,事后证明的确是 ,因为他们的那一套实验虽然复杂但是原理根本不靠谱。
,因为他们的那一套实验虽然复杂但是原理根本不靠谱。
 ,因为他们的那一套实验虽然复杂但是原理根本不靠谱。
,因为他们的那一套实验虽然复杂但是原理根本不靠谱。
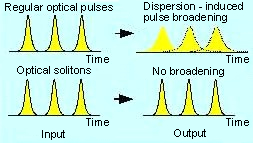
回到光波的队伍传播话题上来。光纤通讯中这就有一个很现实很重要的关键问题:光脉冲在光纤中传播的时候不管拉长还是缩短,最终结果是拉长,都会造成失真,导致接受到的光脉冲信号和发出去的光脉冲信号混淆乃至分不清,从而达不到传输信号的作用。现在使用的妥协办法就是,让前后发出的光脉冲队伍间隔时间加长,这个就算每个光脉冲拉长了,到达终点的时候还能分得开,没有跟后面的队伍混淆一起。所以,现在的光纤通讯都要有中继站,一则补充传输中信号强度的损失,二者重新注入新的光脉冲,这相当于恢复光脉冲队伍的原有形状。比如,北京到广州的火车(或者上海到拉萨)虽有直达特快,但是中途仍然需要停靠以补充用水食品等,高铁通了,这样的折腾减少了,这就是高技术的进步。但是,北京到广州的光纤通讯,还需要很多中继站,好像是让光脉冲的火车停靠以加水加食品,实际上是换了光脉冲的火车而已,信息需要从一列光火车换乘到另一列。如果我们的光纤通讯技术能做到,光脉冲从北京进去直达广州再出来,中间不停靠不换光火车,那就是特别高的高技术了。 这就需要发展光纤通讯的高铁技术——光孤子通讯技术了。所谓的光孤子通信技术,就是发展出特定的光脉冲,在特定的光纤里面传播特别长一段距离,光脉冲的队伍依然很整齐(参见下图左)。这跟高铁跑在专用轨道上一个道理。这里是高技术,也包含了深刻了科学前沿领域。
这就需要发展光纤通讯的高铁技术——光孤子通讯技术了。所谓的光孤子通信技术,就是发展出特定的光脉冲,在特定的光纤里面传播特别长一段距离,光脉冲的队伍依然很整齐(参见下图左)。这跟高铁跑在专用轨道上一个道理。这里是高技术,也包含了深刻了科学前沿领域。
 这就需要发展光纤通讯的高铁技术——光孤子通讯技术了。所谓的光孤子通信技术,就是发展出特定的光脉冲,在特定的光纤里面传播特别长一段距离,光脉冲的队伍依然很整齐(参见下图左)。这跟高铁跑在专用轨道上一个道理。这里是高技术,也包含了深刻了科学前沿领域。
这就需要发展光纤通讯的高铁技术——光孤子通讯技术了。所谓的光孤子通信技术,就是发展出特定的光脉冲,在特定的光纤里面传播特别长一段距离,光脉冲的队伍依然很整齐(参见下图左)。这跟高铁跑在专用轨道上一个道理。这里是高技术,也包含了深刻了科学前沿领域。
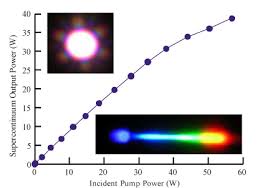
更深刻更科学前沿一点,就再多说一点点本博主的老本行,飞秒激光(femto-second laser)。飞秒激光就是一种非常短的光脉冲,这个光的队伍特别长,就是说对应的光波长(λi)很多,越多光波长加进去这个队伍,这个光脉冲时间就很有可能更短(量子测不准原理决定的)。现在同行都知道,把整个可见光都包括进去都已经很容易了,看起来就是白光,跟太阳光谱非常接近,也就是说,很容易展示出一个飞秒光脉冲,用牛顿的三角棱镜散开以后看到从深蓝到深红都有,技术上这一点都不麻烦(见上图右)。关键问题是,如果管理好这个光频率队伍前进中的整齐度问题,因为这个队伍太容易被拉长而变形得不像样,也就是说保持飞秒的传播很困难,顺便,光孤子通讯技术也在这个领域。顺便多说一句,日常照明的荧光灯的那个白光不是真正的白光,里面包含了太阳白光的几个很窄的波段,用以骗过人的眼睛而已。
那么,能不能包含更多更多的光波长(λi)进来,从而把这个光脉冲的时间变得比飞秒还短?答案是肯定的,absolutely true! 这个新术语就是阿秒(atto-second)。但是,可见光范围内的光波长(λi)还是太长,实现起来特别困难,人们就移到X-射线领域,那里频率非常高就是波长非常短,相对而言可以得到很长的光波队伍,才可能够容易地得到阿秒激光。这个领域是高技术最前沿,也是科学的一大前沿。目前,世界上只有一个课题组宣称得到了阿秒(某西方国家),很多人表示基本认可,但是需要其它课题组重复出来,也就是实验验证。整个世界的主要国家都在努力进行,第二个和后来的结果也许证明第一个结果是对的,那么前两家有可能得到诺奖!如果后来证明第一家的是错误的,那就还需要推倒重来,重新争做世界上第一个阿秒王/阿秒帝。anyway,这个领域需要诺奖,不言而喻!
不好意思,从一个小学生的简单数学问题,扯到了如此的科学和技术前沿,实质就是一个队伍向前行进中的队形问题。

你也可以倒过来说,科学和高技术的前沿,其实也是小学生级别的问题,这样看,大家都是小学生了,难道不是吗?
-
"对称性的意思是事物处在一个状态时测量某种属性结果的概率不依赖于观察者的位置(也即坐标架的选择)。由此Wigner推出对于不同观察者的态之间通过一个幺正或反幺正算符转换。特别地,不同时刻的观察者观察到的态也由一个幺正算符转换"
- 纯态是能表述出希尔伯特空间矢量的量子态;混合态反之。
-
纯态的叠加对应概率幅叠加,混态的叠加对应概率叠加。
留空 2010-07-08 16:31:28
@Lynne: - 可以啊,比如两光子纠缠纯态,对其中一个光子求迹,剩下另一个光子的密度矩阵就是个混态。实际上有人认为混态是大的纯态系统中把环境trace掉以后剩下子系统的不完全描述,有一部分信息在求迹中丢掉了。
[已注销] 2010-07-09 19:46:48
- 纯态各组分之间是相干叠加,而混合态是非相干叠加。
[已注销] 2010-07-07 14:29:19
也就是说,纯态系统可以用一个波函数来描述,这个波函数各成分前的系数模方之和等于1,这是对概率幅的要求。
而混合态各成分之间没有相干性,是一个经典统计的结果,各成分前面系数之和为1,不加平方。这是经典概率的要求。因此混合态不能用一个波函数来描述。
这就是它们密度矩阵平方的迹的差异来源。纯态跟混合态与单量子多量子系统没关系。一个单量子系统也可以处于混合态,只要个成分之间的相干性被破坏。
纯态总可以用完备基矢展开(但纯态和本征态可不是一个概念哦,纯态可不一定是本征态。我们在初量里见到的波函数都是纯态),而混合态只能写成密度矩阵。
-
对Lynne提出两点置疑:
小沐他爸 (星际争霸,终于到了打GG的时候) 2010-07-10 09:35:59
1、“一个单量子系统也可以处于混合态,只要个成分之间的相干性被破坏。” 如何实验上实现,你的回答仍然是从理论上的。事实上,我不认为单个量子系统可以处在混合态,至少实验上是这样,理由下面解释。
2、部分求迹前后该子系统的熵一定是不变的,这个可以证明。所以你说部分求迹后“一部分信息丢掉了”,那么丢掉的是什么信息?这个可以引出另一个问题,部分求迹后得到子系统的密度矩阵,那么我可以通过这个密度矩阵还原出原系统的密度矩阵吗?在某些情况中,答案是,可以,比如DMRG中。
态叠加原理是量子力学的,或者是数学的,而混合态则是热力学的。
绝对零度下显然不存在混合态。上面有人提到混合态是对应概率叠加,把混合态密度矩阵的对角元理解为概率,这是不准确的。用分布应该更好一些。
量子统计中讲到纠缠态的时候,往往会和部分求迹相联系,比如两个二能级系统,纠缠在一起,其中一半的自由度被求和求掉,得到的就是一个混合态。这会给人一个造成一个假象,那就是混态在一个二能级系统中就能出现。
而事实上,这种处理只是数学上的。在某些量子信息的文章中中,部分求迹被叫做adiabatic elimination technique(如:PRL 92,197901),重点在绝热一词,这充分说明了它与热力学相联系的本质。
从物理本源出发,混合态的形成是与热涨落有关的,是热涨落导致了退相干,而退相干则导致了混合态。
情况就是这样。
-
部分求迹前后该子系统的熵一定是不变的,这个可以证明
小沐他爸 (星际争霸,终于到了打GG的时候) 2010-07-11 14:14:50
这个我不太明白了,取包含相关态的完备正交基容易证明纯态熵为一定0,混态熵一定不为0。
===============================================
部分求迹不能把纯态变成混态啊
对某个纯态进行多次重复测量将制备出一个混合态——不同坍缩结果之间不存在任何相位关联,彼此是不相干的。
对于单量子系统能否处于混合态的看法,在概念上没必要划分得太死,量子力学本身就是一个唯象的统计理论嘛。
=================================================
这。。。如果量子力学都是唯象的,那我也没话说了
是不是可以这么认为,称之为混合态,只是因为我们所了解到的信息比较少,使得我们不能用一个波函数来描述这个系统,,当信息足够多的时候就可以认为是一个纯态了。
=================================================
密度矩阵描述的就不是波函数吗?
简单点应该是 纯态把位相的信息丢掉就变成混合态了...但是可以还原成纯态吗?
=================================================
纠缠的纯化的确是很复杂的一件事情 目前应该没有绝对的结论吧 只是具体的情况具体分析
- 部分求迹前后该子系统的熵一定是不变的,这个可以证明。
[已注销] 2010-07-11 22:02:20
==============
不知道你这里说的熵是什么熵。von-Neumann熵对约化前和约化后的密度矩阵显然是不一样的。而von-Neumann熵正好是信息的量度。
我不认为单个量子系统可以处在混合态,至少实验上是这样
==============
比如对于光晶格或射频阱中的单个原子或离子。把基态和第一激发态作为我们考虑的自旋自由度的两个态。在离子自发辐射之前,我们说上下两个能态是相干的,这时候离子处于纯态。但一旦它发生了自发辐射,原子就处于了混合态。这就是为什么量子操作必须在离子的第一激发态能级寿命之内完成。另外,外界环境与离子的相互作用都能使离子发生退相干,导致量子计算无法进行。这些东西在量子光学里可以用主方程描述。
-
不知道你这里说的熵是什么熵。von-Neumann熵对约化前和约化后的密度矩阵显然是不一样的。而von-Neumann熵正好是信息的量度。
小沐他爸 (星际争霸,终于到了打GG的时候) 2010-07-12 09:38:24
=================================
这个显然是从何而来的?
比如对于光晶格或射频阱中的单个原子或离子。把基态和第一激发态作为我们考虑的自旋自由度的两个态。在离子自发辐射之前,我们说上下两个能态是相干的,这时候离子处于纯态。但一旦它发生了自发辐射,原子就处于了混合态。这就是为什么量子操作必须在离子的第一激发态能级寿命之内完成。另外,外界环境与离子的相互作用都能使离子发生退相干,导致量子计算无法进行。这些东西在量子光学里可以用主方程描述。
=================================
第一,你说的仍然是理论 而非实验
据我所知 光晶格的实验技术还没有精确到操控“单个”原子的程度 同样的 量子阱中的一个纳米颗粒 少说也得上百个原子吧
这是实验上真实的情形 至于为什么那些人要声称他们能操控单个二能级系统呢 比如自旋阻塞实验中 他们号称可以一个一个自旋的操控 这实际上本身就隐含了统计的思想 他们利用了一系列复杂的技术手段 比如门电压的精确调控 使得大家处在简并度极高的能级上 再加上强的磁场 使得再上面的能级难以发挥作用等等
总之 实验真实的情况只可能是统计之后的 所以你所说的上能级下能级什么的 都只是理论上理想的模型而已
第二,你觉得概念建立以后 就没必要局限在热力学中 我的观点恰恰相反
比如退相干的问题 这一直是量子信息研究中的关键问题之一 事实上 量子力学中是不可能有退相干的 退相干一定是多体的效应 或者说热的作用
再比如你提到的自发辐射 量子力学中的自发辐射 是爱因斯坦提出的一套唯象的办法来解决的 虽然这套理论非常漂亮 但有很多问题如果不放在统计的框架下 是很难被真正理解的
其实量子力学本来就有概率统计思想在里面。人们对微观粒子所知并不完全。
================================
量子力学的概率你认为是“所知不完全”导致的?或者说,你仍然认为存在隐变量?那好吧 这是另外一个论题了 不在这里讨论
-
如我之前所说,纯态熵一定是1,混态一定小于1.这是很好证明的。
留空 2010-07-13 01:28:41
另外,与其说描述混态必须用引入量子系综,不如说量子系综只是对混态的一种描述工具。就像描述我桌上的一杯水的状态,那我考虑的就是只有一杯水。学过统计力学都知道,联系微观量和宏观量的基本假设是:宏观量等于微观量的时间平均。为了让平均的含义确切,系综理论是一个有效的工具——但真正与实验相联系的、有确切物理意义的是水的体积、温度等物理量的时间平均值,不是那一堆假想的各种“一杯水”。因面前这杯水各物理量的时间平均值等于假想中系综的平均值,系综理论才有效。(不管是因为各态历经理论还是什么原因)从原理上说,我桌上这杯水的状态是给定的,但我还是认为有一个系综分布。
以上的讨论完全适用于量子体系,譬如我面前不是一杯水,是由复杂方式束缚住的费米气体。可见混态之所以“混”,不是因为突然在原先考虑的系统上多出了一整个系综,而不过就是因为对系统的信息不完全而已——换句话说:我们不知道系统确切处于哪个态。否则(不考虑黑洞可能的影响)按照量子力学的基本原理,任何一个孤立系统(包括宇宙)都是处于纯态。至于系综,只是引入并描述这种信息不确定性,并没有什么理论上的根本性。 - 纯态是能表述出希尔伯特空间矢量的量子态;混合态反之。
-
纯态的叠加对应概率幅叠加,混态的叠加对应概率叠加。
留空 2010-07-08 16:31:28
@Lynne: - 可以啊,比如两光子纠缠纯态,对其中一个光子求迹,剩下另一个光子的密度矩阵就是个混态。实际上有人认为混态是大的纯态系统中把环境trace掉以后剩下子系统的不完全描述,有一部分信息在求迹中丢掉了。
[已注销] 2010-07-09 19:46:48
- 纯态各组分之间是相干叠加,而混合态是非相干叠加。
[已注销] 2010-07-07 14:29:19
也就是说,纯态系统可以用一个波函数来描述,这个波函数各成分前的系数模方之和等于1,这是对概率幅的要求。
而混合态各成分之间没有相干性,是一个经典统计的结果,各成分前面系数之和为1,不加平方。这是经典概率的要求。因此混合态不能用一个波函数来描述。
这就是它们密度矩阵平方的迹的差异来源。纯态跟混合态与单量子多量子系统没关系。一个单量子系统也可以处于混合态,只要个成分之间的相干性被破坏。
纯态总可以用完备基矢展开(但纯态和本征态可不是一个概念哦,纯态可不一定是本征态。我们在初量里见到的波函数都是纯态),而混合态只能写成密度矩阵。
-
对Lynne提出两点置疑:
小沐他爸 (星际争霸,终于到了打GG的时候) 2010-07-10 09:35:59
1、“一个单量子系统也可以处于混合态,只要个成分之间的相干性被破坏。” 如何实验上实现,你的回答仍然是从理论上的。事实上,我不认为单个量子系统可以处在混合态,至少实验上是这样,理由下面解释。
2、部分求迹前后该子系统的熵一定是不变的,这个可以证明。所以你说部分求迹后“一部分信息丢掉了”,那么丢掉的是什么信息?这个可以引出另一个问题,部分求迹后得到子系统的密度矩阵,那么我可以通过这个密度矩阵还原出原系统的密度矩阵吗?在某些情况中,答案是,可以,比如DMRG中。
态叠加原理是量子力学的,或者是数学的,而混合态则是热力学的。
绝对零度下显然不存在混合态。上面有人提到混合态是对应概率叠加,把混合态密度矩阵的对角元理解为概率,这是不准确的。用分布应该更好一些。
量子统计中讲到纠缠态的时候,往往会和部分求迹相联系,比如两个二能级系统,纠缠在一起,其中一半的自由度被求和求掉,得到的就是一个混合态。这会给人一个造成一个假象,那就是混态在一个二能级系统中就能出现。
而事实上,这种处理只是数学上的。在某些量子信息的文章中中,部分求迹被叫做adiabatic elimination technique(如:PRL 92,197901),重点在绝热一词,这充分说明了它与热力学相联系的本质。
从物理本源出发,混合态的形成是与热涨落有关的,是热涨落导致了退相干,而退相干则导致了混合态。
情况就是这样。
-
部分求迹前后该子系统的熵一定是不变的,这个可以证明
小沐他爸 (星际争霸,终于到了打GG的时候) 2010-07-11 14:14:50
这个我不太明白了,取包含相关态的完备正交基容易证明纯态熵为一定0,混态熵一定不为0。
===============================================
部分求迹不能把纯态变成混态啊
对某个纯态进行多次重复测量将制备出一个混合态——不同坍缩结果之间不存在任何相位关联,彼此是不相干的。
对于单量子系统能否处于混合态的看法,在概念上没必要划分得太死,量子力学本身就是一个唯象的统计理论嘛。
=================================================
这。。。如果量子力学都是唯象的,那我也没话说了
是不是可以这么认为,称之为混合态,只是因为我们所了解到的信息比较少,使得我们不能用一个波函数来描述这个系统,,当信息足够多的时候就可以认为是一个纯态了。
=================================================
密度矩阵描述的就不是波函数吗?
简单点应该是 纯态把位相的信息丢掉就变成混合态了...但是可以还原成纯态吗?
=================================================
纠缠的纯化的确是很复杂的一件事情 目前应该没有绝对的结论吧 只是具体的情况具体分析
- 部分求迹前后该子系统的熵一定是不变的,这个可以证明。
[已注销] 2010-07-11 22:02:20
==============
不知道你这里说的熵是什么熵。von-Neumann熵对约化前和约化后的密度矩阵显然是不一样的。而von-Neumann熵正好是信息的量度。
我不认为单个量子系统可以处在混合态,至少实验上是这样
==============
比如对于光晶格或射频阱中的单个原子或离子。把基态和第一激发态作为我们考虑的自旋自由度的两个态。在离子自发辐射之前,我们说上下两个能态是相干的,这时候离子处于纯态。但一旦它发生了自发辐射,原子就处于了混合态。这就是为什么量子操作必须在离子的第一激发态能级寿命之内完成。另外,外界环境与离子的相互作用都能使离子发生退相干,导致量子计算无法进行。这些东西在量子光学里可以用主方程描述。
-
不知道你这里说的熵是什么熵。von-Neumann熵对约化前和约化后的密度矩阵显然是不一样的。而von-Neumann熵正好是信息的量度。
小沐他爸 (星际争霸,终于到了打GG的时候) 2010-07-12 09:38:24
=================================
这个显然是从何而来的?
比如对于光晶格或射频阱中的单个原子或离子。把基态和第一激发态作为我们考虑的自旋自由度的两个态。在离子自发辐射之前,我们说上下两个能态是相干的,这时候离子处于纯态。但一旦它发生了自发辐射,原子就处于了混合态。这就是为什么量子操作必须在离子的第一激发态能级寿命之内完成。另外,外界环境与离子的相互作用都能使离子发生退相干,导致量子计算无法进行。这些东西在量子光学里可以用主方程描述。
=================================
第一,你说的仍然是理论 而非实验
据我所知 光晶格的实验技术还没有精确到操控“单个”原子的程度 同样的 量子阱中的一个纳米颗粒 少说也得上百个原子吧
这是实验上真实的情形 至于为什么那些人要声称他们能操控单个二能级系统呢 比如自旋阻塞实验中 他们号称可以一个一个自旋的操控 这实际上本身就隐含了统计的思想 他们利用了一系列复杂的技术手段 比如门电压的精确调控 使得大家处在简并度极高的能级上 再加上强的磁场 使得再上面的能级难以发挥作用等等
总之 实验真实的情况只可能是统计之后的 所以你所说的上能级下能级什么的 都只是理论上理想的模型而已
第二,你觉得概念建立以后 就没必要局限在热力学中 我的观点恰恰相反
比如退相干的问题 这一直是量子信息研究中的关键问题之一 事实上 量子力学中是不可能有退相干的 退相干一定是多体的效应 或者说热的作用
再比如你提到的自发辐射 量子力学中的自发辐射 是爱因斯坦提出的一套唯象的办法来解决的 虽然这套理论非常漂亮 但有很多问题如果不放在统计的框架下 是很难被真正理解的
其实量子力学本来就有概率统计思想在里面。人们对微观粒子所知并不完全。
================================
量子力学的概率你认为是“所知不完全”导致的?或者说,你仍然认为存在隐变量?那好吧 这是另外一个论题了 不在这里讨论
-
如我之前所说,纯态熵一定是1,混态一定小于1.这是很好证明的。
留空 2010-07-13 01:28:41
另外,与其说描述混态必须用引入量子系综,不如说量子系综只是对混态的一种描述工具。就像描述我桌上的一杯水的状态,那我考虑的就是只有一杯水。学过统计力学都知道,联系微观量和宏观量的基本假设是:宏观量等于微观量的时间平均。为了让平均的含义确切,系综理论是一个有效的工具——但真正与实验相联系的、有确切物理意义的是水的体积、温度等物理量的时间平均值,不是那一堆假想的各种“一杯水”。因面前这杯水各物理量的时间平均值等于假想中系综的平均值,系综理论才有效。(不管是因为各态历经理论还是什么原因)从原理上说,我桌上这杯水的状态是给定的,但我还是认为有一个系综分布。
以上的讨论完全适用于量子体系,譬如我面前不是一杯水,是由复杂方式束缚住的费米气体。可见混态之所以“混”,不是因为突然在原先考虑的系统上多出了一整个系综,而不过就是因为对系统的信息不完全而已——换句话说:我们不知道系统确切处于哪个态。否则(不考虑黑洞可能的影响)按照量子力学的基本原理,任何一个孤立系统(包括宇宙)都是处于纯态。至于系综,只是引入并描述这种信息不确定性,并没有什么理论上的根本性。
-
呵呵,纯态熵为1是打错了,你可以看我前面说的。记得我当时花了很多篇幅写非线性和量子力学中不确定性的区别,但你好像只记得我对他们共性的叙述:他们都是在一定信息量情形下无法确定某物理量的最终数值。——而这本来就是一个与物理实质无关的数学性命题。我想其它方面我也没有什么复述的必要,毕竟一个人倾向于选择性健忘,那就没什么能记住的。我很好奇,如果有人说“Wick rotation可以让场论同时用于粒子物理和统计力学”时,你会不会也激动地高呼:粒子物理和场论不是一回事。。。当然,没人说它们是一回事,只是Wick rotation听不到你的抗议。
留空 2010-07-13 15:30:32
不过我还是最后总结一下逻辑:1.热力学系统的定义与系综理论无关。2.宏观物理量的定义不需系综理论帮助。
由上可见,宏观量的涨落实际上也不用系综理论就可以理解。
-
本来想回去把那个老贴翻出来的 想想还是算了 我记得当时无欲说过 这已经变成一个心理学问题了 就是说有的人本来是清楚对方想表达的意思 可总喜欢很作的标新立意
小沐他爸 (星际争霸,终于到了打GG的时候) 2010-07-14 09:54:57
如果你所要表达关于对不确定性、或系综的描述与这句“Wick rotation可以让场论同时用于粒子物理和统计力学”类似 那我也不相信会有人跳出来反驳了
不过很遗憾的是 这里很多时候讨论的都是物理 而非数学 傅立叶变换可以用到的领域更多 但不意味着它所能用到的地方的物理内涵都是相同的 这也正是需要被讨论的部分
与系综理论类似的是量子力学的哥本哈根诠释 没有这些诠释 统计力学和量子力学的数学形式一样运行不悖 所以你的结论我并不认为是错的
关键的问题出在哲学层面 或者科学界的common sense上 没有这些诠释 很多理论都是空中花园 没有牢固的根基 与民科并无本质区别
其实你完全可以坚持传统的热力学定义 统计平均也完全可以不理解为系综平均 当然前提是有人有兴趣陪一个个概念去Argue 如果他有那个闲心的话
纯态熵那个问题 我并不是想抓你的笔误 只是我认为你的理解不对 熵是定义出来的 不同的定义的熵有不同的形式 纯态的熵是不是0 混态的熵是不是一定小于1 这不是可以“证明”的问题 能证明的只是两个系统的熵在同一个定义下进行大小的比较
比如冯诺伊曼熵 如果我把对数的底改一下 那么混态的熵就完全有可能大于1了 这在实际运用时是很常见的 比如有人喜欢用2作底 有人喜欢用自然对数等等 只要你讨论的问题是在同一个定义下就可以了
-
把书上的东西照写一遍本来就没什么意义,既然人家发到网上来问,问的还就是概念,当然就是要你写出你对这个概念的总结。要不直接给他们指出哪本书上有不就行了。
留空 2010-07-14 12:25:25
数学在物理学中本来就有统一概念的意义,比如傅里叶变换虽然可以用到完全不同的领域,但实际上我们可以统一地把它们看做频谱分解。当然这个频谱分解在光学上分解的不同频率,在场论中分解的是不同动量本征态。这时候当人问你:什么是傅里叶分解?的时候。给出一个统一的理解,比起分析不同情况下的细节有价值得多——实际上,后者不可能在网上讨论的时候让人明白清楚,只有足够的训练、实践才能真正帮助提问者。
第一,系综理论是一个数学工具,系综是假想出来的而不是真实存在的。定义一个有物理意义的物理量,不应该用假想的某种结构,而应该用物理世界中实际存在的、可操作性的物理过程。你不是一直在强调物理意义么,可以肯定地说:统计平均的物理意义就是物理量的时间平均,系综平均反而是一种数学意义的平均。这也正符合你说的common sense,因为这一观点在任何一本统计力学教科书上都能查到。
第二,哥本哈根诠释早就风烛残年了,我想退相干历史比它有希望得多。
第三,民科的特点实际上正好和你说得相反——民科大都重诠释,轻理论;重论理,轻实验。它们可以把一个概念翻来覆去说得很麻烦,却提不出任何一个可操作性的实验验证。这与科学界认可(又一个common sense)的“有物理意义的物理量应该以可操作性的物理过程定义”相悖。
当然,熵的定义可以多种多样,von neuman熵只是其中一种。但至少你也没说出哪一个定义符合你所说的“部分求迹熵不变”。(其实你用这个莫须有的定理反驳Lynne的时候,实际上也没有指出用的哪种熵的概念,我只能认为你的意思是所有熵都有这个性质)不管是给von neuman的S加上一个常量,还是乘以一个常数(改变底)都不影响“部分求迹改变熵”这一事实
-
1. 相似变换不改变矩阵的本征值,也不改变迹
Everett (╮(╯▽╰)╭ ~(= ̄ U  ̄=)~) 2010-07-15 10:55:17
2. 部分求迹改变矩阵的本征值,也改变von neuman entropy
别混淆了。
"光子具有自旋角动量和轨道角动量,如果你看不懂这两个词,没关系,只要明白它们是两个自由度就够了。在以前的实验中,传的只是轨道角动量的状态。但是如果你想真正传输一个光子的完整状态,应该把这两个自由度的状态都传过去"
量子力学描述一个粒子的状态,却是给出一个态函数或者称为态矢量,这个态矢量不是位于日常所见的三维空间,而是位于一个数学抽象的线性空间。在这里我们不需要深究这是个什么空间,关键在于两个态矢量之间可以进行“内积”的运算。
量子公设的第三条是对测量下的定义。量子测量可以通过一个测量算符的集合
 来表示,它作用在系统的状态空间上。
来表示,它作用在系统的状态空间上。§2 QFT in practice: 一切都是输入输出!
让我们以一个问题开始,即,作为一种物理(而不是数学或者形而上学)理论,量子场论如何工作。
大体上,和其他物理理论一样,量子场论可被视为输入输出系统。输入和输出端是可观测量,而其内核,则是一套数学公式体系。一种理论的物理意义就在于,将有限的可观测量输入理论后,理论可以通过公式体系的演绎,给出确定的、可供实验与观测检验的输出。至于这理论内核中的概念是否有经验世界的对应物,则不是物理理论所要解决的问题。
在量子场论的情形,输入输出端是关联函数。粒子探测器的计数、材料对激发的响应、宇宙的大尺度结构,这些可观测量在量子场论中都可化为关联函数。因此,将场论与实验观测建立联系,需要做两件事情:一是将观测量与关联函数建立联系,二是用理论计算关联函数。前者依赖于具体应用的场合且与本文关系不大,所以我们假设这一步已经做到,从而将关联函数径直视作可观测量。而后者,就是本文的中心问题。现在让我们讨论之。
至少在本文所关心的情形,关联函数总可被表达成路径积分,且这路径积分总能从配分函数通过泛函微商求得。因此,问题划归为计算配分函数。配分函数也是路径积分,它由两部分构成:被积泛函与积分测度。被积泛函是以经典作用量为相角的纯相位,而积分测度,一般来说是没有定义好的。我们或许可以像定义有限维线性空间的积分测度那样,将每个方向的微分形式简单地“乘”起来,但对于无穷多自由度来讲,这样做没有定义:正如简单地将所有自然数相加没有定义一样。因此需要其它更聪明的方式来定义这个测度。在场论中,为路径积分的测度赋予定义,就叫做正规化
wigner-ville 分布有什么通俗的物理意义吗?
按投票排序按时间排序
2 个回答
什么是答案总结? 答案总结
不太清楚提问者问的具体指什么。。。。如果是我理解的意思,那么可以看下面的解释。
信号分析中的 Wigner-Ville分布,对应于量子物理中的Wigner分布。
它的对称傅里叶变换形式,Weyl分布,是相空间函数到Hilbert空间算符的映射的表达形式。Weyl分布,或Wigner分布,已知其一,可以互推。
对于单qubit,Weyl分布的定义可以推出最基本的Hilbert空间Bloch球的四个参数的表示,同时与pauli算子的表达吻合;对于两qubit,它相当于一个Hademard变换。
较深层次的含义,它表达的使物理体系保持不变的对称变换。这也是Wigner定理的意义:“如果一个使体系在物理上保持不变的变换将体系的每个态矢同时变成另一套态矢,则总可以调节相位,使得对所有态矢,都存在同一个么正变换使得它们对应起来。”
这种变换能将计算基矢的傅里叶变换与本征态下标的变换循环对应起来。而这可以当作态矢Hilbert空间的基本定理。
信号分析中的 Wigner-Ville分布,对应于量子物理中的Wigner分布。
它的对称傅里叶变换形式,Weyl分布,是相空间函数到Hilbert空间算符的映射的表达形式。Weyl分布,或Wigner分布,已知其一,可以互推。
对于单qubit,Weyl分布的定义可以推出最基本的Hilbert空间Bloch球的四个参数的表示,同时与pauli算子的表达吻合;对于两qubit,它相当于一个Hademard变换。
较深层次的含义,它表达的使物理体系保持不变的对称变换。这也是Wigner定理的意义:“如果一个使体系在物理上保持不变的变换将体系的每个态矢同时变成另一套态矢,则总可以调节相位,使得对所有态矢,都存在同一个么正变换使得它们对应起来。”
这种变换能将计算基矢的傅里叶变换与本征态下标的变换循环对应起来。而这可以当作态矢Hilbert空间的基本定理。
[PPT]第八讲
n例如,发射台不断向接受者发射脉冲信号,无论接受者是静止还是在运动,他接收到脉冲的个数是相同的。所以,相位是一个不变量,对不同的观察者不变。这可以通过洛伦兹变换来证明,但在牛顿力学中,根据伽利略变换与多普勒效应无法保证相位不变性。
n相位不变性是德布罗意发现的,它是研究电磁场的相对论效应乃至量子理论的基础。
在闵可夫斯基背景时空中,由局域惯性系的静电学定律就可以建立电动力学的理论体系,闵氏时空的间隔不变性自动导致光速不变与电磁学的洛伦兹协变性§1.2 基本观念
1, 基本图像:de Broglie关系与波粒二象性
1905年Einstein通过提出下列关系
Eh==νωh,kehec
Epvhv
vv===λ (1.9)
(这里π
2h
=
h),引入光子的概念。这在原先认为光是电磁波的图象
上添加了粒子的图象,这已由上节第一组实验所证实。于是,若知道等式右边的波动参数ω和k,便可用这组关系求得它左边的量所相应的微粒子特性。经过18年之久,de Broglie克服积习的约束,逆过来理解这组关系,将上面这组关系从针对m=0的情况推广到m≠0的情况,提出原先是微粒的微观粒子也具有波动性1,
粒子参数E和pv
作者:bellbasis 时间:2010-07-18 23:34:52
作者:圆周率谐音 回复日期:2010-07-18 20:34:10
首先,你还是要从概率上理解量子力学,而不是波动上。通常的机械波,比如水的表面波,是一个一个挨在一起的水分子震荡,形成的宏观的波动图样。
概率波(你所说的物质波)是单个粒子在空间中出现的概率幅度对应的图样。不是说这个粒子必须一扭一扭地前进。
我们说概率波,说的是复数的概率波形势,概率波的实际观测量都是绝对值的平方,所以有的时候我们看不见波动效应,只是因为概率波绝对值平方是看不出周期规律的。
举个例子,你观测水表面波的时候,波的振幅对应量子力学的粒子的波函数振幅,但是波上每个质点的能量,对应量子力学观测量。你计算一下能量(平均振幅平方)就发现水面的能量分布式均匀的,没有波的形状。
而发生干涉时,水面有的地方振幅永远是0,就是这里的能量也永远是0,画成能量分布图样,就出现干涉条文了。
所以,根本作用的是波的振幅及其相位(波函数),观测结果是振幅平方的分布,所以相互作用的时候是先叠加波函数,再绝对值平方,这个时候就出现干涉了。
静止只是自由运动的一个变换而已(换个参考系而已)没有特殊性。这是物理学基本原理。
下面说量子力学。
自由状态下,动量守恒,所以波函数是exp(-ipx),p是常数,它的绝对值平方才代表可观测的概率,所以是1, 就是说在x方向上个点出现几率相同。所以自由粒子状态下,你看不见“波的图样”,看见的只是一条直线。(波表现在ipx上,因为exp(it)可以写成三角函数,那个是描述波动的,但是因为可观测量是绝对值平方,所以此时观测不到波动的现象)另外,你看不见绝对静止的粒子的绝对位置,因为绝对静止意味着动量为0,而意味着其坐标是无限弥散的(不确定原理),用函数delta(p)表示。
相对论情况下,有相对论量子力学,量子场论表述。波动方程里的变量都是洛伦茨协变的,满足狭义相对论的洛伦茨变换规律。
混合态只能写成密度矩阵
纯态各分量间的相对相位(不是整体相位)是意义的,但是在混态里没相对相位了,各分量间没有了干涉。
欢迎大家指出错误。
我对这个不理解:
“一个单量子系统也可以处于混合态,只要个成分之间的相干性被破坏。”
这种状态实验上能实现吗?
本征态和纯态?
来自: Logogogo(Pig has Dreams) 2010-07-07 09:42:59
这两个概念在文字描述上好像是一样的:某CSCO的共同本征态。但主要问题是,怎么理解叠加态和混合态?它们似乎都是描述一个系统处在各个本征态的概率的,我的理解是:叠加态是描述单量子系统的,而混合态是描述多量子系统的。那为什么它们的密度矩阵的平方的差异又是怎么来的?看着数学结果摸不透物理意思,真是杯具…
作者:bellbasis 时间:2010-07-18 23:34:52
作者:圆周率谐音 回复日期:2010-07-18 20:34:10
首先,你还是要从概率上理解量子力学,而不是波动上。通常的机械波,比如水的表面波,是一个一个挨在一起的水分子震荡,形成的宏观的波动图样。
概率波(你所说的物质波)是单个粒子在空间中出现的概率幅度对应的图样。不是说这个粒子必须一扭一扭地前进。
我们说概率波,说的是复数的概率波形势,概率波的实际观测量都是绝对值的平方,所以有的时候我们看不见波动效应,只是因为概率波绝对值平方是看不出周期规律的。
举个例子,你观测水表面波的时候,波的振幅对应量子力学的粒子的波函数振幅,但是波上每个质点的能量,对应量子力学观测量。你计算一下能量(平均振幅平方)就发现水面的能量分布式均匀的,没有波的形状。
而发生干涉时,水面有的地方振幅永远是0,就是这里的能量也永远是0,画成能量分布图样,就出现干涉条文了。
所以,根本作用的是波的振幅及其相位(波函数),观测结果是振幅平方的分布,所以相互作用的时候是先叠加波函数,再绝对值平方,这个时候就出现干涉了。
静止只是自由运动的一个变换而已(换个参考系而已)没有特殊性。这是物理学基本原理。
下面说量子力学。
自由状态下,动量守恒,所以波函数是exp(-ipx),p是常数,它的绝对值平方才代表可观测的概率,所以是1, 就是说在x方向上个点出现几率相同。所以自由粒子状态下,你看不见“波的图样”,看见的只是一条直线。(波表现在ipx上,因为exp(it)可以写成三角函数,那个是描述波动的,但是因为可观测量是绝对值平方,所以此时观测不到波动的现象)另外,你看不见绝对静止的粒子的绝对位置,因为绝对静止意味着动量为0,而意味着其坐标是无限弥散的(不确定原理),用函数delta(p)表示。
相对论情况下,有相对论量子力学,量子场论表述。波动方程里的变量都是洛伦茨协变的,满足狭义相对论的洛伦茨变换规律。
混合态只能写成密度矩阵
纯态各分量间的相对相位(不是整体相位)是意义的,但是在混态里没相对相位了,各分量间没有了干涉。
欢迎大家指出错误。
我对这个不理解:
“一个单量子系统也可以处于混合态,只要个成分之间的相干性被破坏。”
这种状态实验上能实现吗?
本征态和纯态?
来自: Logogogo(Pig has Dreams) 2010-07-07 09:42:59
这两个概念在文字描述上好像是一样的:某CSCO的共同本征态。但主要问题是,怎么理解叠加态和混合态?它们似乎都是描述一个系统处在各个本征态的概率的,我的理解是:叠加态是描述单量子系统的,而混合态是描述多量子系统的。那为什么它们的密度矩阵的平方的差异又是怎么来的?看着数学结果摸不透物理意思,真是杯具…
n例如,发射台不断向接受者发射脉冲信号,无论接受者是静止还是在运动,他接收到脉冲的个数是相同的。所以,相位是一个不变量,对不同的观察者不变。这可以通过洛伦兹变换来证明,但在牛顿力学中,根据伽利略变换与多普勒效应无法保证相位不变性。
n相位不变性是德布罗意发现的,它是研究电磁场的相对论效应乃至量子理论的基础。
在闵可夫斯基背景时空中,由局域惯性系的静电学定律就可以建立电动力学的理论体系,闵氏时空的间隔不变性自动导致光速不变与电磁学的洛伦兹协变性§1.2 基本观念
1, 基本图像:de Broglie关系与波粒二象性
1905年Einstein通过提出下列关系
Eh==νωh,kehec
Epvhv
vv===λ (1.9)
(这里π
2h
=
h),引入光子的概念。这在原先认为光是电磁波的图象
上添加了粒子的图象,这已由上节第一组实验所证实。于是,若知道等式右边的波动参数ω和k,便可用这组关系求得它左边的量所相应的微粒子特性。经过18年之久,de Broglie克服积习的约束,逆过来理解这组关系,将上面这组关系从针对m=0的情况推广到m≠0的情况,提出原先是微粒的微观粒子也具有波动性1,
设想有一只碗,碗底形状就好比是势能函数U(x,y),往碗里倒水,每一点的水深h(x,y)就是一个和空间坐标有关的函数,且取决于势
经典力学的谐振子与薛定谔方程的谐振子解
初等量子力学中,在讲到薛定谔方程时,一般都会求解几个势场作为范例,其中就包含了谐振子解。刚才在豆瓣上看到有人提问,似乎对这个解的含义不甚明了。
量子力学中的波函数Ψ(t,x,y,z),可以看作一个经典场。这个经典场的特别之处在于其统计诠释,不过在这里可以不管这个。薛定谔方程决定了波函数在时空中的分布,即以(t,x,y,z)为变量,Ψ的函数形式。在定态情形,波函数可分离变量:Ψ(t,x,y,z) = χ(t)ψ(x,y,z),因此定态薛定谔方程其实给定了一个经典场ψ(x,y,z)在空间中的分布。当然这个分布和势能表达式是有关的,因为定态薛定谔方程中有势能项。打个并不贴切的比方:设想有一只碗,碗底形状就好比是势能函数U(x,y),往碗里倒水,每一点的水深h(x,y)就是一个和空间坐标有关的函数,且取决于势能分布。假如碗底的形状有二次形式:U = (1/2)mω(x^2 + y^2),就意味着势能有谐振子形式。倒入一定高度的水(相当于总能量给定),就不难写出此时h(x,y)的表达式。
谐振子的定态波函数解也是差不多的意思,只不过求解过程要更复杂些,最终求得的,是在谐振子这个势场中,波函数经典场的空间分布函数。
定态波函数解和力学中一个动来动去的谐振子有很大不同。定态波函数解的意义已在上面叙述。而经典力学的谐振子,可以理解成一个波包在势场中运动,它的波函数Ψ(t,x,y,z)也是薛定谔方程的解,但却不是定态薛定谔方程的解。
将Ψ(0,x)(只考虑一维,t = 0时的波包)用能量基矢展开:Ψ(0,x) = c_{n}Ψ_{n}(0,x) ,等号右边要对n求和。其中Ψ_{n}(t,x) = Ψ_{n}(0,x) exp(-iE_{n}t),因此Ψ(t,x) = c_{n}Ψ_{n}(0,x)exp(-iE_{n}t) (等号右边对n求和)。这里的含时项不能从和式中提出,因此Ψ(t,x)不能分离变量,也无法得到关于Ψ(t,x)的定态薛定谔方程。但可以计算各能量本征态的演化,叠加而成Ψ(t,x)的演化规律,从而得到波包的运动图像。这个图像可以和经典谐振子做类比
作者:bellbasis 时间:2010-07-18 05:43:08
作者:bellbasis 时间:2010-07-18 05:43:08
说下我的看法,希望对楼主有帮助。
首先你要理解概率。
1对于粒子,你仍然可以理解成点粒子,但是它出现在一定空间,一定时间,一定动量区间的由概率描述,其概率分布图样表现成波动的外观。粒子沿经典的直线行走,是因为在当前的相互作用下,沿其他路径行走的概率几乎为0。(路径积分的一种解释是走其他路径的概率都干涉相消了)。
2粒子干涉的时候,实际上是粒子出现的概率分布改变了。
3数学上说,粒子由一个抽象的态来描述|phi>, 当我们需要讨论粒子的空间波函数的时候,作用左矢<x|phi> 当我们需要讨论动量分布的时候,作用左矢<p|phi>表征动量分布。所以粒子的空间分布,动量分布,都是由一个态在一种观测下的投影。表示这个投影的函数,就是描述粒子这种概率分布形状的函数(这个函数是复函数,实际上观测的概率分布是要求绝对值平方的)
4,没有相互作用的时候,空间波函数的解是平面波(这是理想状况。实际上任何粒子都是平面波的叠加)有相互作用的时候,可以是共振态,很多短寿命的粒子都是共振态,就是出现极短的时间后,这种特殊的粒子就消失了(衰变成其他相对稳定的粒子)。
5,你只要着重理解概率分布就可以了,它不能预言每个粒子的行为,但是能预言大量粒子的统计行为。而不需要去理解具体一个粒子是如何波动的。
先说这么多。
首先你要理解概率。
1对于粒子,你仍然可以理解成点粒子,但是它出现在一定空间,一定时间,一定动量区间的由概率描述,其概率分布图样表现成波动的外观。粒子沿经典的直线行走,是因为在当前的相互作用下,沿其他路径行走的概率几乎为0。(路径积分的一种解释是走其他路径的概率都干涉相消了)。
2粒子干涉的时候,实际上是粒子出现的概率分布改变了。
3数学上说,粒子由一个抽象的态来描述|phi>, 当我们需要讨论粒子的空间波函数的时候,作用左矢<x|phi> 当我们需要讨论动量分布的时候,作用左矢<p|phi>表征动量分布。所以粒子的空间分布,动量分布,都是由一个态在一种观测下的投影。表示这个投影的函数,就是描述粒子这种概率分布形状的函数(这个函数是复函数,实际上观测的概率分布是要求绝对值平方的)
4,没有相互作用的时候,空间波函数的解是平面波(这是理想状况。实际上任何粒子都是平面波的叠加)有相互作用的时候,可以是共振态,很多短寿命的粒子都是共振态,就是出现极短的时间后,这种特殊的粒子就消失了(衰变成其他相对稳定的粒子)。
5,你只要着重理解概率分布就可以了,它不能预言每个粒子的行为,但是能预言大量粒子的统计行为。而不需要去理解具体一个粒子是如何波动的。
先说这么多。
作者:bellbasis 时间:2010-07-18 23:34:52
作者:圆周率谐音 回复日期:2010-07-18 20:34:10
首先,你还是要从概率上理解量子力学,而不是波动上。通常的机械波,比如水的表面波,是一个一个挨在一起的水分子震荡,形成的宏观的波动图样。
概率波(你所说的物质波)是单个粒子在空间中出现的概率幅度对应的图样。不是说这个粒子必须一扭一扭地前进。
我们说概率波,说的是复数的概率波形势,概率波的实际观测量都是绝对值的平方,所以有的时候我们看不见波动效应,只是因为概率波绝对值平方是看不出周期规律的。
举个例子,你观测水表面波的时候,波的振幅对应量子力学的粒子的波函数振幅,但是波上每个质点的能量,对应量子力学观测量。你计算一下能量(平均振幅平方)就发现水面的能量分布式均匀的,没有波的形状。
而发生干涉时,水面有的地方振幅永远是0,就是这里的能量也永远是0,画成能量分布图样,就出现干涉条文了。
所以,根本作用的是波的振幅及其相位(波函数),观测结果是振幅平方的分布,所以相互作用的时候是先叠加波函数,再绝对值平方,这个时候就出现干涉了。
静止只是自由运动的一个变换而已(换个参考系而已)没有特殊性。这是物理学基本原理。
下面说量子力学。
自由状态下,动量守恒,所以波函数是exp(-ipx),p是常数,它的绝对值平方才代表可观测的概率,所以是1, 就是说在x方向上个点出现几率相同。所以自由粒子状态下,你看不见“波的图样”,看见的只是一条直线。(波表现在ipx上,因为exp(it)可以写成三角函数,那个是描述波动的,但是因为可观测量是绝对值平方,所以此时观测不到波动的现象)另外,你看不见绝对静止的粒子的绝对位置,因为绝对静止意味着动量为0,而意味着其坐标是无限弥散的(不确定原理),用函数delta(p)表示。
相对论情况下,有相对论量子力学,量子场论表述。波动方程里的变量都是洛伦茨协变的,满足狭义相对论的洛伦茨变换规律。
作者:圆周率谐音 回复日期:2010-07-18 20:34:10
首先,你还是要从概率上理解量子力学,而不是波动上。通常的机械波,比如水的表面波,是一个一个挨在一起的水分子震荡,形成的宏观的波动图样。
概率波(你所说的物质波)是单个粒子在空间中出现的概率幅度对应的图样。不是说这个粒子必须一扭一扭地前进。
我们说概率波,说的是复数的概率波形势,概率波的实际观测量都是绝对值的平方,所以有的时候我们看不见波动效应,只是因为概率波绝对值平方是看不出周期规律的。
举个例子,你观测水表面波的时候,波的振幅对应量子力学的粒子的波函数振幅,但是波上每个质点的能量,对应量子力学观测量。你计算一下能量(平均振幅平方)就发现水面的能量分布式均匀的,没有波的形状。
而发生干涉时,水面有的地方振幅永远是0,就是这里的能量也永远是0,画成能量分布图样,就出现干涉条文了。
所以,根本作用的是波的振幅及其相位(波函数),观测结果是振幅平方的分布,所以相互作用的时候是先叠加波函数,再绝对值平方,这个时候就出现干涉了。
静止只是自由运动的一个变换而已(换个参考系而已)没有特殊性。这是物理学基本原理。
下面说量子力学。
自由状态下,动量守恒,所以波函数是exp(-ipx),p是常数,它的绝对值平方才代表可观测的概率,所以是1, 就是说在x方向上个点出现几率相同。所以自由粒子状态下,你看不见“波的图样”,看见的只是一条直线。(波表现在ipx上,因为exp(it)可以写成三角函数,那个是描述波动的,但是因为可观测量是绝对值平方,所以此时观测不到波动的现象)另外,你看不见绝对静止的粒子的绝对位置,因为绝对静止意味着动量为0,而意味着其坐标是无限弥散的(不确定原理),用函数delta(p)表示。
相对论情况下,有相对论量子力学,量子场论表述。波动方程里的变量都是洛伦茨协变的,满足狭义相对论的洛伦茨变换规律。
作者:bellbasis 时间:2010-07-20 23:35:28
可见,量子力学中,两种静止的含义是完全不同的。区分了两种情形,一切的矛盾就不复存在。
===============================
这并没有不同的定义,只是因为不确定原理,你不能同时确定一个粒子的动量和位置而已。也就是说你不能找到一个静止的坐标固定的粒子。只能说当你找到一个坐标固定的粒子时,你不知道它的动量是多大。即不知道它是不是静止。
经典情况下,确定动量和位置的手段都很粗糙,所以可以找到近似静止和近似固定位置的粒子。矛盾只在于精度。
实际上,量子力学有3个解释,薛定谔方程,矩阵力学,路径积分。
第一个和经典类似,很直观,由微分方程表示,只是微分方程的解用量子力学诠释物理意义。
第二个用更数学化,用于理解量子理学概念,进行形式推导更好。其核心思想是粒子用态矢量表示,算符作用于态矢量,需要和测量联系的时候只是求态矢内积。
第三个很强大,认为量子和经典效应是所有可能的粒子路径的叠加。但是计算起来并不简单。
实际上第二种一般出现的场合比较多,因为概念明晰。量子场论也可以认为是和空间,动量相关的算符作用于粒子态上的结果。
粒子态是一种抽象状态,可以用动量,坐标等等表述粒子态的特征。该态可以在坐标,动量上投影,其投影为波函数。
所以,更好的描述是,粒子处于一种状态,经过物理算符作用后变成另一种状态,然后和其他状态进行内积求出需要观测的物理量(由一个态到另一个态的几率)。
所以这个时候其实和“波“并没什么关系,只是其概率分布长得很像波而已。
===============================
这并没有不同的定义,只是因为不确定原理,你不能同时确定一个粒子的动量和位置而已。也就是说你不能找到一个静止的坐标固定的粒子。只能说当你找到一个坐标固定的粒子时,你不知道它的动量是多大。即不知道它是不是静止。
经典情况下,确定动量和位置的手段都很粗糙,所以可以找到近似静止和近似固定位置的粒子。矛盾只在于精度。
实际上,量子力学有3个解释,薛定谔方程,矩阵力学,路径积分。
第一个和经典类似,很直观,由微分方程表示,只是微分方程的解用量子力学诠释物理意义。
第二个用更数学化,用于理解量子理学概念,进行形式推导更好。其核心思想是粒子用态矢量表示,算符作用于态矢量,需要和测量联系的时候只是求态矢内积。
第三个很强大,认为量子和经典效应是所有可能的粒子路径的叠加。但是计算起来并不简单。
实际上第二种一般出现的场合比较多,因为概念明晰。量子场论也可以认为是和空间,动量相关的算符作用于粒子态上的结果。
粒子态是一种抽象状态,可以用动量,坐标等等表述粒子态的特征。该态可以在坐标,动量上投影,其投影为波函数。
所以,更好的描述是,粒子处于一种状态,经过物理算符作用后变成另一种状态,然后和其他状态进行内积求出需要观测的物理量(由一个态到另一个态的几率)。
所以这个时候其实和“波“并没什么关系,只是其概率分布长得很像波而已。
作者:bellbasis 时间:2010-07-21 16:09:31
作者:袁士霄 回复日期:2010-07-21 14:30:09
静止的唯一定义是动量为0~ 我没有限定不能实用 delta(x),我只是说delta(x)不是静止粒子而已。
参考系变换,非相对论情况变化的是v,也就是p,p从+变成0 变成-没什么问题阿?很连续阿?(这时请考察该静止粒子的幅度绝对值平方有没有变化,exp(-ipx),无论p是什么,绝对值都是1)相对论情况,波矢和坐标p,x都是协变/逆变的,px是标量和坐标变换无关,所以和非相对论情况一样。
我前面说过,测量量是振幅的绝对值平方,不是波动复数表达形式本身,楼主把它的平方安参考系变换,再看看有没有变化(那个才是可以和经典类比的东西)。
我一直强调,要理解量子力学,要从态和概率上理解,波动表达形式只是选择参数空间后的一种数学展开(数学描述),并不是本质的。所以不要纠结于和机械波进行类比。2者没有关系 。只是量子力学的数学形式在某些特殊的态下呈现波动的特征而已
静止的唯一定义是动量为0~ 我没有限定不能实用 delta(x),我只是说delta(x)不是静止粒子而已。
参考系变换,非相对论情况变化的是v,也就是p,p从+变成0 变成-没什么问题阿?很连续阿?(这时请考察该静止粒子的幅度绝对值平方有没有变化,exp(-ipx),无论p是什么,绝对值都是1)相对论情况,波矢和坐标p,x都是协变/逆变的,px是标量和坐标变换无关,所以和非相对论情况一样。
我前面说过,测量量是振幅的绝对值平方,不是波动复数表达形式本身,楼主把它的平方安参考系变换,再看看有没有变化(那个才是可以和经典类比的东西)。
我一直强调,要理解量子力学,要从态和概率上理解,波动表达形式只是选择参数空间后的一种数学展开(数学描述),并不是本质的。所以不要纠结于和机械波进行类比。2者没有关系 。只是量子力学的数学形式在某些特殊的态下呈现波动的特征而已
举报 | 回复
作者:bellbasis 时间:2010-07-22 03:09:45
bellbasis你说<"所以这个时候其实和“波“并没什么关系,只是其概率分布长得很像波而已。>
本帖子就是说波的,量子力学也从有波起家的,所以把"波"一脚踢开,总有些不厚道,我认为这可不仅仅是吃水不忘挖井人的一个问题,所以你应该像袁怪侠那样说"并不能因此而认为:物质是主体,波只是它的附属。",呵呵.
=================
是这样的,也许早期理论探索阶段需要借助波动来理解量子力学,但是当体系完善之后并不需要时时考虑这种事情,波动的“效应”包含在解之中。波动形式的引入只是一种中间状态,整个逻辑出发于粒子态,终结于测量的物理量。波动只是中间的数学手段而已。
还有,位置不确定和静止不矛盾。位置不确定说的是你不知道它静止在什么地方,但是它是静止的。对于无数个粒子统计平均后,你会发现这些粒子均匀分布在空间中。这来自量子力学的基本原理。这种效应只有在极其微观才能发现。过度到经典的时候,你不能找到这么一个动量非常精确的平面波,那么你也就可能找到一个位置不那么弥散的准静止粒子,同理,对于delta(x)的情况,经典的情况是你不可能找到一个delta(x)的粒子(位置测量没那么精确)比如可能是一个高斯波包,那么粒子被限定在一个小范围内,同时也允许你测量它的动量,可能也是一个中心在0的高斯波包,那么就是说你能在一定精度内看见一个准静止,准固定位置的粒子,这就是我们的日常生活。
实际上,delta《-》exp(-ipx)是2种极端精确的情况。只有在微观尺度下,才能看见这种极端精确的现象。
本帖子就是说波的,量子力学也从有波起家的,所以把"波"一脚踢开,总有些不厚道,我认为这可不仅仅是吃水不忘挖井人的一个问题,所以你应该像袁怪侠那样说"并不能因此而认为:物质是主体,波只是它的附属。",呵呵.
=================
是这样的,也许早期理论探索阶段需要借助波动来理解量子力学,但是当体系完善之后并不需要时时考虑这种事情,波动的“效应”包含在解之中。波动形式的引入只是一种中间状态,整个逻辑出发于粒子态,终结于测量的物理量。波动只是中间的数学手段而已。
还有,位置不确定和静止不矛盾。位置不确定说的是你不知道它静止在什么地方,但是它是静止的。对于无数个粒子统计平均后,你会发现这些粒子均匀分布在空间中。这来自量子力学的基本原理。这种效应只有在极其微观才能发现。过度到经典的时候,你不能找到这么一个动量非常精确的平面波,那么你也就可能找到一个位置不那么弥散的准静止粒子,同理,对于delta(x)的情况,经典的情况是你不可能找到一个delta(x)的粒子(位置测量没那么精确)比如可能是一个高斯波包,那么粒子被限定在一个小范围内,同时也允许你测量它的动量,可能也是一个中心在0的高斯波包,那么就是说你能在一定精度内看见一个准静止,准固定位置的粒子,这就是我们的日常生活。
实际上,delta《-》exp(-ipx)是2种极端精确的情况。只有在微观尺度下,才能看见这种极端精确的现象。
作者:bellbasis 时间:2010-07-22 16:06:20
作者:bellbasis 回复日期:2010-07-22 03:09:45
bellbasis你也一定程度的认可“高斯波包”对应粒子实在,可怪侠不这么认为,这可不能含糊,这是个很根本的问题,不仅仅是个认知论问题,而是从根本上认知世界的出发点的问题,他是对构建什么更本质性场论以及物理何去何从的方向性问题。当今在科学界对“高斯波包”的认可度能占几成呢?
====================
....................在粒子物理里面,探测器观测到的物理量都是这种高斯波包……因为探测器的精度是有限的。
袁前辈的意思是,一个函数可以fourier展开成平面波叠加,例如delta(x)展开成exp(ipx)的叠加,无穷个动量各不相同的平面波叠加。这只是一种数学手段。我们是否观测到这种平面波(哪个动量分量)取决于我们是否需要测量动量……如果不需要的话,跟本不需要展开。我不知道你对fourier展开有多少了解,但是这和量子力学无关,这只是一种数学而已,在电子电路里面经常用到(当然还有laplace变换),你先想一想这种变换在电路中对电信号的处理,能不能理解,能不能通过你的逻辑。高斯波包的fourier对应变换是高斯波包,所以我们能同时测量坐标和动量(一定精度上)。
另外,我觉得你的问题还是没有理解静止的定义,delta(x)和delta(p)的区别在哪里。如果我们不谈论delta(x),就没有以上问题了。还有,我强调无论粒子以什么波形出现,那只是概率分布图样,不是粒子就是那个样子的……
bellbasis你也一定程度的认可“高斯波包”对应粒子实在,可怪侠不这么认为,这可不能含糊,这是个很根本的问题,不仅仅是个认知论问题,而是从根本上认知世界的出发点的问题,他是对构建什么更本质性场论以及物理何去何从的方向性问题。当今在科学界对“高斯波包”的认可度能占几成呢?
====================
....................在粒子物理里面,探测器观测到的物理量都是这种高斯波包……因为探测器的精度是有限的。
袁前辈的意思是,一个函数可以fourier展开成平面波叠加,例如delta(x)展开成exp(ipx)的叠加,无穷个动量各不相同的平面波叠加。这只是一种数学手段。我们是否观测到这种平面波(哪个动量分量)取决于我们是否需要测量动量……如果不需要的话,跟本不需要展开。我不知道你对fourier展开有多少了解,但是这和量子力学无关,这只是一种数学而已,在电子电路里面经常用到(当然还有laplace变换),你先想一想这种变换在电路中对电信号的处理,能不能理解,能不能通过你的逻辑。高斯波包的fourier对应变换是高斯波包,所以我们能同时测量坐标和动量(一定精度上)。
另外,我觉得你的问题还是没有理解静止的定义,delta(x)和delta(p)的区别在哪里。如果我们不谈论delta(x),就没有以上问题了。还有,我强调无论粒子以什么波形出现,那只是概率分布图样,不是粒子就是那个样子的……
作者:bellbasis 时间:2010-07-22 19:19:35
作者:bellbasis 回复日期:2010-07-22 16:06:20
================================
在一般意义上可用数学方式无穷级数展开,但这里好像不是首先对一个成型函数的展开,而是直接假想出的一种跟数学无穷级数类似的数学模型,当然也只有这样,才能所谓解决类似孤波子不散的理论基础.所以在这里一切都好像本末倒置了,而按你说的,它是对一个什么样子函数实施无穷级数展开的呢?
=============
能使用这个模型,来自于量子力学的基本假设之一,x p的对易关系(p的算符化)。
如果承认这点,后面的都是自然的事情了。
我觉得你一直没明白一件事情,粒子还是粒子,一个粒子不会“散开“即使是平面波。
散开的是粒子出现的概率分布,不是粒子本身。
================================
在一般意义上可用数学方式无穷级数展开,但这里好像不是首先对一个成型函数的展开,而是直接假想出的一种跟数学无穷级数类似的数学模型,当然也只有这样,才能所谓解决类似孤波子不散的理论基础.所以在这里一切都好像本末倒置了,而按你说的,它是对一个什么样子函数实施无穷级数展开的呢?
=============
能使用这个模型,来自于量子力学的基本假设之一,x p的对易关系(p的算符化)。
如果承认这点,后面的都是自然的事情了。
我觉得你一直没明白一件事情,粒子还是粒子,一个粒子不会“散开“即使是平面波。
散开的是粒子出现的概率分布,不是粒子本身。
作者:bellbasis 时间:2010-07-22 20:09:32
作者:圆周率谐音 回复日期:2010-07-22 19:41:32
作者:bellbasis 回复日期:2010-07-22 19:19:35
========================
你可能理解错了我说的"散开"这个意思了.
用于表示能量消散,产生辐射,损失能量,只要涉及到波的稳定,这是首当其中考虑的.
===========================
关于能量变化的问题,量子力学认为,最基本的是粒子态,当态不变的时候,能量也不变,能量的变化(态的变化)必然来自于外界的相互作用。辐射的产生来自于,比如一磁场中运动的电子,时刻和磁场(光子)交换着能量。电子的态发生连续变化,那么可能产生辐射。
束缚态的时候,电子可以存在的态是分立的(薛定谔方程的解),意味着不是任何能量的光子都能使得电子从一个态变成另一个态,那么大多数时候也就没法辐射了。
也许你对量子力学的一些基本假设产生疑问?那么只能说实验证明了这些假设的正确,
作者:bellbasis 回复日期:2010-07-22 19:19:35
========================
你可能理解错了我说的"散开"这个意思了.
用于表示能量消散,产生辐射,损失能量,只要涉及到波的稳定,这是首当其中考虑的.
===========================
关于能量变化的问题,量子力学认为,最基本的是粒子态,当态不变的时候,能量也不变,能量的变化(态的变化)必然来自于外界的相互作用。辐射的产生来自于,比如一磁场中运动的电子,时刻和磁场(光子)交换着能量。电子的态发生连续变化,那么可能产生辐射。
束缚态的时候,电子可以存在的态是分立的(薛定谔方程的解),意味着不是任何能量的光子都能使得电子从一个态变成另一个态,那么大多数时候也就没法辐射了。
也许你对量子力学的一些基本假设产生疑问?那么只能说实验证明了这些假设的正确,
作者:bellbasis 时间:2010-07-22 20:19:24
你试试这个逻辑
量子力学基本原理-》薛定谔方程的解-》电子可以存在的状态(其他状态概率为0)-》氢原子情况下是分立的状态的概率分布||自由电子情况下是连续平面波状态的概率分布(只有这里才出现了波)
所以物质波只是一种早期想法,只是量子力学的一个解。你要问氢原子情况下的相速度是没什么意思的,氢原子情况下是只是一种特殊的分布而已。当然这时粒子的速度是可以求得的,但是和平面波没有什么直接关系。
量子力学基本原理-》薛定谔方程的解-》电子可以存在的状态(其他状态概率为0)-》氢原子情况下是分立的状态的概率分布||自由电子情况下是连续平面波状态的概率分布(只有这里才出现了波)
所以物质波只是一种早期想法,只是量子力学的一个解。你要问氢原子情况下的相速度是没什么意思的,氢原子情况下是只是一种特殊的分布而已。当然这时粒子的速度是可以求得的,但是和平面波没有什么直接关系。
作者:bellbasis 时间:2010-07-22 20:31:52
束缚态的时候,电子可以存在的态是分立的(薛定谔方程的解),意味着不是任何能量的光子都能使得电子从一个态变成另一个态,那么大多数时候也就没法辐射了。
=======================
少数的时候是光子能量刚好等于能级的差别……
=======================
少数的时候是光子能量刚好等于能级的差别……
作者:bellbasis 时间:2010-07-22 20:37:43
作者:bellbasis 回复日期:2010-07-22 20:19:24
你在量子力学里舍弃"波"的概念,就像谈论电脑舍弃与或门等电路,舍弃二进位制,从表面上看,你是正确的.
==================
不一样,撇开数学,波本身不是什么基本的东西,一大堆粒子相互作用的集合的现象而已。
何况概率波和机械波没什么关系,只是用了同样的数学而已。
概率波的效应包含在量子力学的解里面。
好比我们讨论电脑的工作原理,却不需要讨论office2003有什么问题一样。哪怕也许有的人第一次接触电脑用的是office2003
你在量子力学里舍弃"波"的概念,就像谈论电脑舍弃与或门等电路,舍弃二进位制,从表面上看,你是正确的.
==================
不一样,撇开数学,波本身不是什么基本的东西,一大堆粒子相互作用的集合的现象而已。
何况概率波和机械波没什么关系,只是用了同样的数学而已。
概率波的效应包含在量子力学的解里面。
好比我们讨论电脑的工作原理,却不需要讨论office2003有什么问题一样。哪怕也许有的人第一次接触电脑用的是office2003
作者:bellbasis 时间:2010-07-22 20:41:28
作者:bellbasis 回复日期:2010-07-22 20:31:52
少数的时候是光子能量刚好等于能级的差别……
===============================
如果用刚好这个说法的化,世界上没有刚好的能级光子来碰的,所以,也就不可能发生态的跳跃
=============================================
我们不可能完全处于绝对精确的那种能级的本征态(实际上是有宽度的,不过和能级之间的宽度相比很小而已),还有实验精度问题。而入射光子也不是单纯平面波,其动量是一个高斯分布,涵盖了需要跃迁能级的区间就可以了。
少数的时候是光子能量刚好等于能级的差别……
===============================
如果用刚好这个说法的化,世界上没有刚好的能级光子来碰的,所以,也就不可能发生态的跳跃
=============================================
我们不可能完全处于绝对精确的那种能级的本征态(实际上是有宽度的,不过和能级之间的宽度相比很小而已),还有实验精度问题。而入射光子也不是单纯平面波,其动量是一个高斯分布,涵盖了需要跃迁能级的区间就可以了。
作者:bellbasis 时间:2010-07-22 20:48:20
作者:圆周率谐音 回复日期:2010-07-22 20:41:55
所以把波当成敲门砖,不可能那么侥幸,肘起裤子不认帐,没那么容易.
===========================
科学研究早期的摸索阶段用一些类比是很正常的,但是类比不是等同,你明白这点就可以了。其中最大的不同在于,机械波必须有介质,是介质中物质的相互作用效应,但是概率波不需要“介质“它只是概率分布而已。
所以把波当成敲门砖,不可能那么侥幸,肘起裤子不认帐,没那么容易.
===========================
科学研究早期的摸索阶段用一些类比是很正常的,但是类比不是等同,你明白这点就可以了。其中最大的不同在于,机械波必须有介质,是介质中物质的相互作用效应,但是概率波不需要“介质“它只是概率分布而已。
作者:bellbasis 时间:2010-07-22 21:12:40
那么请问你,除了数学形式之外,量子力学哪里必须要用波的概念了?
定态的解无非是列出方程之后解方程而已。其解是驻波形式而已。其他更多情况下的解都不是驻波或者平面波形式,非要用波的概念去强行理解这些解么?那只是一种概率分布图样而已。
定态的解无非是列出方程之后解方程而已。其解是驻波形式而已。其他更多情况下的解都不是驻波或者平面波形式,非要用波的概念去强行理解这些解么?那只是一种概率分布图样而已。
作者:bellbasis 时间:2010-07-22 21:23:53
举个例子,伽利略证明2个质量不同的物体可以同时落地,牛顿力学完全可以解释这一现象并给出其他推测,诸如人造卫星运行轨迹。但是你如果要用2个质量不同的物体同时落地去理解为什么人造卫星是这么运动的。当然理解不了。因为你的出发点就不是根本的,只是一个结论而已。所以你用驻波和平面波去理解氢原子基态波函数,谐振子波函数,肯定不明白了。
举报 | 回复
作者:bellbasis 时间:2010-07-22 22:15:25
量子力学基本原理
1: 态矢量描述例子态
2: 算符描述物理量
3: 对易关系
4: 薛定谔方程
5: 全同粒子原理。
足够了解方程了。
不需要引入波的概念
1: 态矢量描述例子态
2: 算符描述物理量
3: 对易关系
4: 薛定谔方程
5: 全同粒子原理。
足够了解方程了。
不需要引入波的概念
所以说波粒二相性,关键在于“相”上,只是一种观测结果,不是本质。其本质就是由概率描述的粒子而已。所以科普的时候很多人以为这种矛盾综合的结果是本质,实际上不是。
bellbasis 时间:2010-07-22 23:16:54
作者:圆周率谐音 回复日期:2010-07-22 22:50:49
说简单些,定态是量子力学的最重要工程目标,而定态的理论基础是驻波,你说波算老几呢?
===================
无所谓,方程和边界条件列出来了,解出什么是什么,解出驻波是驻波,解出合流超比函数就是氢原子。这只是一个数学问题。一个概率分布函数而已。我没有否认量子力学采用了波的数学形式。但那并不重要。一个量子系统重要的是我们知道概率分布和物理量(平均值),波的数学形式只是中间过程。
作者:圆周率谐音 回复日期:2010-07-22 22:50:49
说简单些,定态是量子力学的最重要工程目标,而定态的理论基础是驻波,你说波算老几呢?
===================
无所谓,方程和边界条件列出来了,解出什么是什么,解出驻波是驻波,解出合流超比函数就是氢原子。这只是一个数学问题。一个概率分布函数而已。我没有否认量子力学采用了波的数学形式。但那并不重要。一个量子系统重要的是我们知道概率分布和物理量(平均值),波的数学形式只是中间过程。
作者:bellbasis 时间:2010-07-27 23:51:45
作者:袁士霄 回复日期:2010-07-27 17:22:07
==================
薛定谔定态方程的建立确实没有直接借助当时由驻波计算出的各种能级公式,这一点我确实说错了,但薛定谔在建立薛定谔定态方程的时候使用了,Ψ(x,t) = ψ(x)f(t),而ψ(x)f(t)的数学形式所形成的图像Ψ(x,t) 应该是一个驻波数学图形,所以薛定谔也毕竟是根据当时依据驻波定态的思维模式,殊途同归,并有摘取别人成果果实的嫌疑,而建立的定态薛定谔方程。请你给进一步评述。
================
关于薛定谔方程的建立,先猜出自由粒子对应平面波,然后根据H=P^2/2M ,猜出p对应的算符和t对应的算符。得出自由粒子薛定谔方程。这个时候,你也学可以说借鉴了波,(自由粒子是平面波么),但是引入势能项之后,方程的解就五花八门什么都可以了,平面波或者驻波很多时候就没法解释了。所以楼主有疑问。这个时候,就是纯粹的解方程了,和什么波没什么关系了。
所以当量子理学体系完善以后。我们喜欢用算符做基本假设,而不是平面波做基本假设。因为算符的基本假设逻辑上更根本。平面波只是一个解,驻波也只是一个解,更多时候是非常复杂的乱七八糟函数的解。
==================
薛定谔定态方程的建立确实没有直接借助当时由驻波计算出的各种能级公式,这一点我确实说错了,但薛定谔在建立薛定谔定态方程的时候使用了,Ψ(x,t) = ψ(x)f(t),而ψ(x)f(t)的数学形式所形成的图像Ψ(x,t) 应该是一个驻波数学图形,所以薛定谔也毕竟是根据当时依据驻波定态的思维模式,殊途同归,并有摘取别人成果果实的嫌疑,而建立的定态薛定谔方程。请你给进一步评述。
================
关于薛定谔方程的建立,先猜出自由粒子对应平面波,然后根据H=P^2/2M ,猜出p对应的算符和t对应的算符。得出自由粒子薛定谔方程。这个时候,你也学可以说借鉴了波,(自由粒子是平面波么),但是引入势能项之后,方程的解就五花八门什么都可以了,平面波或者驻波很多时候就没法解释了。所以楼主有疑问。这个时候,就是纯粹的解方程了,和什么波没什么关系了。
所以当量子理学体系完善以后。我们喜欢用算符做基本假设,而不是平面波做基本假设。因为算符的基本假设逻辑上更根本。平面波只是一个解,驻波也只是一个解,更多时候是非常复杂的乱七八糟函数的解。
作者:bellbasis 时间:2010-07-28 01:07:36
作者:圆周率谐音 回复日期:2010-07-28 00:11:20
作者:bellbasis 回复日期:2010-07-27 23:51:45
=====================
方程是人脑思维判断推理的继续,但方程必须有很多的基本数学原理来构建。但人们单靠数学原理也能解决很多的问题,比如民间有很多的数字数学游戏,他们虽然不懂方程,但只要足够聪明,他们也能得出结果,而我们知道这类问题使用方程一般再简单不过了,这就说明方程这个工具的威力,但这种威力跟其建构方程的原理是两码事。
====================
实际上是这个思路:
1: 观测实验,觉得粒子有波动性,猜测自由粒子是平面波,并做一些简单预言。
2: 通过平面波,和薛定谔方程(H|psi>=E|psi>,这个方程很抽象,解决不了任何问题),猜测这个抽象方程的现实对应,即p为坐标的偏微分,E为时间的偏微分。即确定力学量和算符的对应关系。
3:写出H的一般形式,即H包含任何形式的势能。利用偏微分算符,原则上可以解出任何波函数的解,但是这个解不一定是平面波或者驻波,可以是任何东西(引入势能是经典力学哈密顿量要求的,必须有动能项和势能项,你的一切分歧都来此于此,但是这一项是经典要求,不是量子要求)。
4:实验验证一些复杂的解,比如氢原子,比如谐振子,等等,发现和实验相符。
5:确立力学量对应算符作为基本原理。
类比一下这个逻辑:
1, 牛顿看见重物下落
2, 牛顿认为万有引力
3, 牛顿观察开普勒3定律觉得万有引力是平方反比(不记得是不是这样了)
4, 牛顿确定万有引力公式
5, 万有引力公式作为牛顿力学基本原理之一
最初得到定律的时候,需要一些启发性思维和类比(比如你所说的数字游戏),(比如波动的引入)但是不代表一开始的启发性思维就是整个理论框架的基础。苹果,开普勒3定律都是基本定律描述现象的一个子集,但是他们不能描述其他的东西,所以不是基本的。所以说平面波和驻波有他们存在的地方,但是绝对不是基本的。试图用这个解释一切,是不可能的。
在接触未知世界的时候,第一次观察(接触)会让我们有很多灵感,对于暂时不能列出方程描述的东西,我们会用类比去描述未知事物,但是当充分了解之后,必然有更基本的概念,第一次看见的东西仅仅是微不足道的一小部分而已。你理解了么?
所以你跟着物质波的思路历程,经历的只是发现定律的原初思维,而不是看见了完整的量子力学框架。其实很多科普的手法就是如此的(因为框架总是要涉及方程,方程总是枯燥的),比如非常经典的时空的弯曲用一个膜来描述,但是你能用一个重物和膜去真正计算出黑洞的引力场么?无论你怎么摆弄那个重物恐怕都不行吧。
作者:bellbasis 回复日期:2010-07-27 23:51:45
=====================
方程是人脑思维判断推理的继续,但方程必须有很多的基本数学原理来构建。但人们单靠数学原理也能解决很多的问题,比如民间有很多的数字数学游戏,他们虽然不懂方程,但只要足够聪明,他们也能得出结果,而我们知道这类问题使用方程一般再简单不过了,这就说明方程这个工具的威力,但这种威力跟其建构方程的原理是两码事。
====================
实际上是这个思路:
1: 观测实验,觉得粒子有波动性,猜测自由粒子是平面波,并做一些简单预言。
2: 通过平面波,和薛定谔方程(H|psi>=E|psi>,这个方程很抽象,解决不了任何问题),猜测这个抽象方程的现实对应,即p为坐标的偏微分,E为时间的偏微分。即确定力学量和算符的对应关系。
3:写出H的一般形式,即H包含任何形式的势能。利用偏微分算符,原则上可以解出任何波函数的解,但是这个解不一定是平面波或者驻波,可以是任何东西(引入势能是经典力学哈密顿量要求的,必须有动能项和势能项,你的一切分歧都来此于此,但是这一项是经典要求,不是量子要求)。
4:实验验证一些复杂的解,比如氢原子,比如谐振子,等等,发现和实验相符。
5:确立力学量对应算符作为基本原理。
类比一下这个逻辑:
1, 牛顿看见重物下落
2, 牛顿认为万有引力
3, 牛顿观察开普勒3定律觉得万有引力是平方反比(不记得是不是这样了)
4, 牛顿确定万有引力公式
5, 万有引力公式作为牛顿力学基本原理之一
最初得到定律的时候,需要一些启发性思维和类比(比如你所说的数字游戏),(比如波动的引入)但是不代表一开始的启发性思维就是整个理论框架的基础。苹果,开普勒3定律都是基本定律描述现象的一个子集,但是他们不能描述其他的东西,所以不是基本的。所以说平面波和驻波有他们存在的地方,但是绝对不是基本的。试图用这个解释一切,是不可能的。
在接触未知世界的时候,第一次观察(接触)会让我们有很多灵感,对于暂时不能列出方程描述的东西,我们会用类比去描述未知事物,但是当充分了解之后,必然有更基本的概念,第一次看见的东西仅仅是微不足道的一小部分而已。你理解了么?
所以你跟着物质波的思路历程,经历的只是发现定律的原初思维,而不是看见了完整的量子力学框架。其实很多科普的手法就是如此的(因为框架总是要涉及方程,方程总是枯燥的),比如非常经典的时空的弯曲用一个膜来描述,但是你能用一个重物和膜去真正计算出黑洞的引力场么?无论你怎么摆弄那个重物恐怕都不行吧。
作者:bellbasis 时间:2010-07-28 01:29:48
所以说,原初发现定律的时候的思路,和科学体系成熟时的思路是完全不同的。原初发现定律的思路是非常难以理解的,那都是天才的思维,一些结论虽然怪异,但是居然是大部分是正确的。当体系成熟以后,我们不需要天天用那种思维去解决问题
PDF]PDF全文 - 热学精品课程
我来说说 [ 达闻奇 ] 于:2014-06-22 08:34:12 复:4022404
PDF]PDF全文 - 热学精品课程
为矩阵),把系统所有可允许的态,成对地联结起来. 量子力学的倒易定理[5]证明:当系统的哈密顿量与时间明显无关时,由时. 间反演对称性可引出原过程的跃迁概率 ...
对称性和热学*
包科达1) 刘锦城2)
摘要 试图探索一条不同于传统做法的、概括和表述热学基本定律的途径.从理论上,把热学置于对称性原理的基础之上,加以概括和解释 关键词时间和空间平移对称性;时间反演对称性;守恒律;对称破缺 分类号 O 414.1
SYMMETRY AND HEAT
Bao Keda1) Liu Jincheng2) ( 1) Department of Physics, Peking University, Beijing, 100871, China; 2) Pingxiang Specialized School, Pingxiang, Jiangxi, 337055, China)
Abstract In this paper we try to explore a way for summalizing and expressing the fundamental laws of heat, entirelly different from the usual practices. The heat will be generalized and described on the principles of symmetry. Key words time and space translation symmetry; time reversal symmetry; conservation law; symmetry breaking
1 引言
对称性原理在物理学中的基础地位,正越来越受到物理学家的重视从单纯地将对称性看作对物理现象可能性的一种限制,转向把它作为确立物理定律的一块基石.整个物理学的发展,就是物理学家通过大量精确的实验观测和深入的理论分析,揭示各种制约自然界物理现象的基本规律,例如力学的牛顿三定律,热学的热力学第一、二、三定律,电磁学的麦克斯韦方程组等.近年来的研究揭示,贯穿于物理学各分支领域里的这些规律中,还存在一些概括性更高的法则,对称性原理就是其中主要的一个.诺贝尔奖得主和对称性原理的主要阐述者之一的Eugene Wigner[1]把对称性与自然定律之间的关系,类比于自然定律与单个事件之间的关系时说:・对称性原理为自然定律提供的构造和相关性,恰似自然定律自身为一组事件提供的构造和相关性.・那末,对称性原理与热学或热物理学(包括热力学和统计物理学)之间有什么关系?我们能否把对称性看作制约热物理学建立和发展的、概括性更高的法则换句话说,我们能否从对称性原理出发引出热学的基础定律?本文试图就此作一些剖析,以引起各界的关注和讨论
2 对称性
尽管可以认为,对称考虑从科学思想产生和发展的一开始,就是科学家的一个基础性的考虑,但直到20世纪量子力学建立和发展之前,对对称性的认识,多数仍仅限于直感的事物对称性的几何方面,把它看作限制物理过程的一种可能性.例如:圆球绕通过它中心的任意轴的转动是对称的;它对含中心的任意平面的反射和对通过中心的反演是对称的;一个立方体绕通过面心轴的四度旋转下是对称的.由于圆球在旋转任意角度下是对称的,旋转角可取任意值,因此圆球的旋转对称性是连续的;反之,上述立方体的旋转对称是离散的.即使依据这样一
些简单的对称性概念,人们就可以避开物理学基本定律,而对物理现象作出合乎实验观测的分析,例如:由简单的对称性分析可知,有心力作用下的行星轨道一定在一个平面内;平衡态气体的时空对称性必导致麦克斯韦的速度分布律;利用对称性可证明,无限长均匀带电直导线周围的电场必垂直导线表面,且呈径向分布;无限长密绕螺线管在空间任意一点产生的磁场与其轴线平行等等. 然而,稍为深入分析几何对称性就会发现,每一个几何对称性在数学上可用一种坐标变换来加以描述,例如对-y平面的反射操作,对应于x→x′,y→y′和z→-z′的变换;而绕轴的四度旋转操作,可通过→y′,y→x′和z→z′加以表述.上述圆球和立方体相对这两种操作都是对称的,这一事实反映在圆球方程和确定立方体的数学关系式相对上列两种变换是不变的. 现若将从几何对称性获得的有关对称性、对称操作和坐标变换等概念,推广应用到更为普遍的情况:一组变量的一种变换定义一个对称操作,若这些变量的函数通过变换后的形式不变,那末就说此函数相对这种操作是对称的.这样,若表述一个物理定律的数学公式在与某种操作相应的变换下保持不变,则该定律相对此操作是对称的.最常用的对称操作有平移、转动、镜像反射、标度变换等空间操作和时间平移、反演等时间操作.例如:对于一个其中的力只是位置函数的力学系统,牛顿运动方程f=m(d2r/dt2)在时间反演操作(r→r′,t→-t′)下是对称的,叫做时间反演对称性.它预示系统中允许的任何运动,必有逆向的运动设想有一盒录像带,记录了月球上宇航员抛射向上的一个球,随后在引力作用下落到表面.那末,不论是正向还是反向放映这盒录像带,观众看起来,都是等同的.而地球的大气层中存在的粘滞阻力,破坏了这种时间反演对称性.由此可见,一个特定系统的动力学行为的对称性是受到动力学方程和决定力的势能函数的性质所制
约的.对于量子力学问题,尽管动力学方程变得略为抽象,牛顿运动方程为薛定谔波动方程所取代,但对称性原理是相同的,薛定谔方程相对时间反演操作也是对称的.
3 内特(Noether)定理
把上述对称性分析应用于力学系统时发现,由此可以引出一些意义深远的结果:一个力学系统动力学行为的每一个对称性都意味着该系统的一个守恒律,这个结论现在称为内特定理,以纪念首创人德国数学家Emmy Noether(1882~1935年). 任何系统的机械运动都是在一定时空中发生的,故当描述一个系统的机械运动时,总是相对一定参考系说的.一般说,不同参考系中的运动规律,不尽相同.惯性参考系是最简单的一种参考系,其中时空是均匀和各向同性的,自由物体在其中或永远静止,或以恒速作直线运动 惯性系中的时间均匀性,要求其中发生的机械运动相对时间的平移操作变换→t+t0不变,即具有时间平移对称性.在物理上,这意味着,若保持封闭的质点系中每个质点的初始位置和速度不变,系统的动力学行为并不会因时间平移而改变由此时间均匀性引出的后果是,封闭系统的势能函数Ep与时间明显无关,即()=0,从而得到dEp=,故封闭质点系的机械能守恒:恒量,这样,内特定理从时间平移对称性预言存在一个守恒量,称它为系统的能量[2].相应的,空间均匀性和各向同性要求惯性系中发生的动力学行为,相对空间平移操作r→r+r0和转动操作φ→φ+φ0不变,即具有空
则系统的运动状态不变,故系统内力在此位移下所作的总功应为零:,从而引出牛顿第三定律=0,得到封闭质点系的动量守恒定律.空间转动对称性要求空间各取向等效,故角位移δφ后系统内力的总功应为零:,即系统的总力矩为零,从而得到封闭质点系的角动量守恒定律.综上所述,对于一个互作用势能只与质点之间相对位置有关的质点系的时间、空间均匀性及其各向同性的深刻物理后果是系统的能量、动量和角动量守恒,这恰是内特定理要说明的. 倘若我们再依据因果律,把时空均匀性和各向同性,即时空平移对称性和转动对称性,看作原因的对称性,而系统的能量、动量和角动量守恒律看作结果的对称性,则可引出结论:原因中的对称性必反映在结果中,这就是对称性原理,首先由P.居里于1894年提出. 间的平移和转动对称性.空间平移对称性要求空间各点等价,即若有一个封闭的力学系统,其中所有的质点都位移δr,Fij+Fji[3]
4 时间平移对称性和热力学第一定律
两者之间的关系是显而易见的,因为后者表明,对于任一热力学系统必存在一个态函数内能,对于孤立系内能守恒.从微观的意义讲,系统的内能就是组成它的所有粒子的无规则热运动的动能和它们之间相互作用的势能之和. 对于系统的温度、体积和粒子数恒定的正则系综,内能是一个可涨落的量.由于宏观物体包含的粒子数十分巨大,宏观观测的时间和空间的特征尺度较之原子、分子运动的相应特征量大很多,故实验观测到的内能仍取确定的数值,是系统能量的统计平均值,与时间无关 当我们在时间平移对称性基础上,重新认识能量守恒定律时,再简略回顾一
下人们对它的发现和认识是富有启发性的.确认守恒量能量的存在,始于1693年,当时莱布尼茨(Leibniz)观测到,地球重力场中质点的能量(1/2)mv\+2+mgh是一个守恒量.随后的物理学史上不止一次地发生过,在新的物理过程中似乎一部分能量湮没或者无中生有地产生出来,后来的物理学发展又总能确立一种新的能量形式,补偿似已消失或冒出来的那一部分能量,能量守恒定律始终巍然屹立.例如焦耳(Joule)经过几十年的艰辛努力,测定了热功当量,确认热也是一种能量存在的形式.带电体周围的电场具有电场能.燃烧获得的热量来源于物质结构的化学能.1905年爱因斯坦(Einstein)把能量与物质的静止质量联系起来,导出了著名的质能关系式E=mc2.不久,物理学家发现,原子核裂变过程中释放出的能量与相应的质量亏损是符合此关系式的.特别值得一提的是,为了解释β衰变过程中消失掉的那一部分能量,泡利(Pauli)于1931年提出伴随核内中子蜕变为质子和电子的同时,必有一种未被认识的粒子;后来意大利物理学家费米(Fermi)把这种中性且静止质量为零的粒子命名为中微子,从而找回了那一部分丢失的能量,能量守恒定律依旧成立.
5 空间平移和转动对称性与广义的热力学第一定律
当我们确认内特定理,把热力学第一定律和存在态函数内能寓于时间平移对称性中时,自然会联想到,共有7个可加的运动积分,为什么只有能量在热学中起重要作用?而不是动量和角动量?事实是由于传统的因素,我们惯于讨论宏观静止的系统一旦当天文学家应用热物理学于旋转的巨大天体,如银河系时,系统的动量和角动量的作用,将和能量一样,变得十分重要.一个广义的正则系综的概率密度ρi(Ei,pi,Ji,V,N)可写为
ρi=Z-1exp(-βEi-λp.pi-λJ.Ji)
其中Ei,pi和Ji分别表示系统微观态的能量、动量和角动量;而β、λp和λJ分别为相应量的拉格朗日乘子;Z(β,λp,λJ,N,V)是配分函数.因此,广义热力学第一定律应该是时空平移和转动对称性的一个后果.
6 对称破缺和戈德斯通(Goldstone)定理
热力学中还存在一些状态参量,如体积、磁矩、电矩和摩尔数等,它们又是如何从对称性分析中产生出来的?回答是它们存在的基础是对称破缺和戈德斯通定理.譬如体积这个几何状态参量,它与对称破缺概念的联系,可通过晶体的形成过程加以说明.以固态的二氧化碳干冰)晶体为例,在・无限大・的气态O2中,随温度下降而在某局域形成晶核的过程,从对称性观点看,是系统从一个具有连续的完全对称性的气态转变为一个只有离散的较低对称性的固态的过程.在这类晶核化过程中,系统对称性突然自发地降低,称为系统的对称性的・破缺・.从固体物理学我们知道,晶体的振动模式可用波数k=2π/λ和圆频率ω(k)加以描述.长波模式变为简单的声波,并有线性关系ω=vk,故极端模式是在空间均匀的模式,振动频率趋向于零.此时半波长内就包含很多原胞,它们整体地沿同一方向运动,因此晶体可以近似地看成连续介质,而且具有确定的体积著名的物理学家P.W.安德森(Anderson)把这种对称破缺系统具有一个激发谱,当波长趋向无穷时,频率趋向零的性质概括为戈德斯通定理[4]. 相类似地在一些电极化材料例如HCl晶体中,位于格点上的HCl分子中,氢离子围绕相对大的氯离子转动,形成电偶极矩.在转变温度以上,这些电矩的取向是无序的;转变温度以下,偶极矩取向趋向有序,整个晶体拥有净电矩.晶体
从具有较高对称性的状态自发地降低对称性,转变为电矩具有确定轴取向的较低对称性的状态根据戈德斯通定理,这种对称破缺必将导致一个波长为无穷时零频率的元激发在极化晶体中,这类元激发由在净电矩指向附近轴的微小摆动形成的振荡波组成.类似的情况,在居里点附近的铁磁材料中也发生,从而在磁介质热力学中可以引进状态参量总的磁矩.
7 时间反演对称性和细致平衡原理
最后,我们用对称性原理来审视统计物理学的基石・・等概率原理:孤立系达到平衡态时,系统处于任一可能微观运动状态的概率相等.恰是在等概率原理的基础上,才引出了微正则、正则和巨正则分布的极值性质,即在相应的宏观限制条件下,这些分布对应的微观态数目Ω最大,再把熵定义为正比于ln Ω的态函数,从而得出达到平衡态的系统熵最大,构成热力学第二定律的熵增加原理的表述. 一个热力学系统的可允许的微观态,在经典描述中,可用6N维相宇空间里的一个相点表示;在量子描述中,用系统可存在的量子态表示.当系统在外界的扰动下发生微观态之间各种可能的跃迁时,在相宇中勾划出一条迂回曲折、飘忽不定的轨迹.若系统某时刻处于i微观态,随后在外界扰动下跃迁到j态,单位时间里的跃迁概率为ij,这些跃迁概率{pij}在状态空间中构造一个网络在数学上表示为矩阵,把系统所有可允许的态,成对地联结起来. 量子力学的倒易定理[5]证明:当系统的哈密顿量与时间明显无关时,由时间反演对称性可引出原过程的跃迁概率等于逆过程的跃迁概率,即pij=pji.统计物理学中把此倒易定理称为细致平衡原理,它是时间反演对称性的直接后果.显然
是条件概率,表示开始处于i态的系统跃迁到j态的概率.故若用f表示系统处于态的概率,则单位时间里跃迁离开状态的总数正比于;相类似地单位时间里跃迁到状态的总数与成比例.若再考虑到平衡态系统处于i态的概率在时间里是稳恒的,则有 piji
当满足细致平衡时,则对所有状态有fi=fj=Ω-1,这就是等概率原理. 可以设想如此的图象:系统在一切可允许的微观态之间发生各种可能的跃迁,某些态被频繁地访问很大),另一些只偶尔被访问;一些状态一旦被系统达到后,不易变更(很小),又有一些状态却要求系统赶快离开它.但由于时间反演对称性,要求达到平衡态的孤立系中,那些只偶尔被访问的态,一定是系统不易变更的态;而那些频繁被访问的态,只允许对它的短暂入主.恰是这种互相抵消的特征,保证了系统处于任一可能微观态的概率相等.由此可见,等概率原理是系统时间反演对称性的一个后果.
8 对称性和选择定则
应用等概率原理分析实际问题时,还必须注意出现零跃迁边界的可能性.零跃迁边界把系统的状态空间譬如说相宇,划分为两个区域,其间不能发生穿越零跃迁边界的跃迁量子理论证明,出现零跃迁边界的物理原因是另一种对称性发挥了作用,并把这种跃迁概率为零的现象称为选择定则实际上,选择定则映射一种对称性,起源于守恒律[6].譬如,由空间平移对称性引出的动量守恒律要求的选择定则为:末态动量等于初态动量加微扰动量时,跃迁才会发生,否则跃迁
概率为零.由时间平移对称性引出的能量守恒律要求的选择定则为:终态能量等于初态能量加微扰能量.又如在有心力场中运动的电子的选择定则为:角量子数Δl=l′-l=±1,磁量子数Δm=m′-m=0,±1等. 由此可见,为了使热力学的描述完全且有效,必须将能表征状态空间各个分隔区域的全部状态参量包括进来,否则就会引出与实验不一致的结论例如,人们在研究低温下气态氢的热学性质时,就曾发生过这类情况[7].氢分子的两个核的自旋,可因其取向平行或反平行而区别为正氢和仲氢它们的对称性很不相同,前者相对于垂直分子轴的平面的反射操作是对称的,而后者只相对分子中心的反演操作才具有对称性.选择定则禁止两者之间的转变,故若忽视了这一选择定则,就会导致热力学的不完全描述,引出氢气热力学性质的不正确预言.有趣的是,实验表明,若在氢气中掺进少量的氧或水蒸汽,由于这些气体分子的顺磁性,与氢分子核自旋之间的相互作用,破坏产生选择定则的对称性,从而使得正氢和仲氢之间可互相转变,把氢处理为单一气体的热力学描述又变为完全和有效. 因此,热力学描述的完全性在于确定系统的相关的状态空间时,必须考虑它的所有的对称性.每一个新揭示的对称性,在引进新的状态参量的同时,将热力学的应用范围扩大.从此意义上讲,是否可以在对称性原理的层次上把热物理学概括为一门研究从物理系统的对称性引出的,对物质的热运动可能具有性质的制约的学科.
作者单位: 1) 北京大学物理系,北京 100871; 2) 萍乡专科学校,江西萍乡337055 *原国家教委面向21世纪教学内容和课程体系改革研究项目(编号02-4-5)
9 参考文献
[1] Wigner E. Symmetry and Conservation Low. Physics Today, 1964,34 (3) [2] Мамъееъ А Н.Механпка ц Теорцл Омноспмеlъносмц.20e u3g. u3g. 《Внсшал шкоlа》,1986, 148 [3] 赵凯华,罗蔚茵.新概念物理教程 第一卷:力学.北京:高等教育出版社,1995.146 [4] Anderson P W. Concepts in Solids. N.Y: Benjamin Inc, 1964. 175 [5] 张启仁.量子力学.北京:高等教育出版社,1989.286 [6] 邹鹏程.量子力学.北京:高等教育出版社,1989.第六、七、八章 [7] Callen H B. Thermodynamics and an Introduction to Thermo-statistics. second edition. John Wiley & Sons, Inc, 1985
收稿日期:1998-06-15 我来说说 [ 达闻奇 ] 于:2014-06-22 08:34:12 复:4022404
那个特斯拉的帖子,受制于单一要素论的思维方式:一切的问题靠生产力发展,那么生产力怎么发展呢?靠科技,如果科技发展不起来?那么拿钱砸。怎么让人拿钱呢?靠想法。如果别人不接受呢?那就看你忽悠的本事。于是得出了个画饼能力大过天的结论。
暂且不去谈单一要素论。即便特斯拉真有那么大的画饼能力,他要做的事情比苹果难上一百倍一千倍,不说马斯克,哪怕乔布斯再世,以苹果目前的现金流,都未必能做成。
回过头来说楼主的观点,我觉得楼主总结的基本比较全面,按天地人的格局来说,楼主对天地的主导作用阐述的比较透彻。对于人,楼主主要是以分工来概括。
我觉得分工是一个方面。我认为还有另一条规律:纵观所有国家和族群的崛起,都少不了内部某一个阶层/集团/群体,以超越本集团的格局和眼光,并以超强执行力带动整个族群向前迈进。
那么这样一个阶层到底是什么呢?在韦伯的《新教伦理与资本主义精神》中是这么描述的:
这就是韦伯笔下西欧资本主义初期的企业家形象。韦伯甚至神来之笔的描绘了这些人在引领社会前进时所遭受的那些误解和曲解:
而在日本明治维新时期,这样的阶层是由商人和武士所构成的:
本尼迪克特写作《菊与刀》时二战刚结束,她可能还未来得及了解中国的情况。中国崛起的领导者——中国共产党,其主要成分是来自社会底层的农民,以及农民出身的军官、知识分子阶层。这些阶层的共同点,即我上面所说的,能超越本集团的利益,放下一时的得失,带动整个族群。
TG在创建新中国的过程中做出了巨大牺牲——无论政党还是军队。建国后,仍然不断有某个阶层为整体发展让渡部分利益的行为——如农民的剪刀差,工人阶级的下岗,现在又轮到城市中产阶级。这些未必是自觉自愿的——谁叫中国不能走向外掠夺的道路——但却是实实在在的。
古今中外,产业升级无不受到既得利益阶层的阻扰。可用的办法无非是战争,革命
Weinberg量子场论阅读笔记 ——写在四读Weinberg I之后
量子公设的第三条是对测量下的定义。量子测量可以通过一个测量算符的集合 来表示,它作用在系统的状态空间上。
来表示,它作用在系统的状态空间上。
科普量子瞬间传输技术,包你懂!
Make it easy: 历史求和 及 拓扑量子场论2013年07月07日 14:45:32
暂且不去谈单一要素论。即便特斯拉真有那么大的画饼能力,他要做的事情比苹果难上一百倍一千倍,不说马斯克,哪怕乔布斯再世,以苹果目前的现金流,都未必能做成。
回过头来说楼主的观点,我觉得楼主总结的基本比较全面,按天地人的格局来说,楼主对天地的主导作用阐述的比较透彻。对于人,楼主主要是以分工来概括。
我觉得分工是一个方面。我认为还有另一条规律:纵观所有国家和族群的崛起,都少不了内部某一个阶层/集团/群体,以超越本集团的格局和眼光,并以超强执行力带动整个族群向前迈进。
那么这样一个阶层到底是什么呢?在韦伯的《新教伦理与资本主义精神》中是这么描述的:
有一天,闲适自在的生活突然之间中断了,并且常常是劳动组织形式没有发生本质的改变,如变家庭工场为统一领导下的工厂,变手工织为机织一类的改变。相反,出现的新情况无非就是某一个出身于放利家庭的年轻人来到乡下,仔细挑选了他将要雇用的织工,大大加强了对他们的劳动监督,于是便把他们从农民变成了工人。另一方面,他还尽最大可能直接深入到最终消费者中去,以此来改变自己的销售方法。他对一切细节都能了如指掌。他每年还要走访顾客,征求他们的意见。最重要的是,他还调整产品的质量,直接投合他们的需要和愿望。同时他开始介绍廉价多销的原则。这种理性化过程的结果是,那些不愿这样做的人只得关门歇业。这一结果随时随地均可反复见到。在残酷竞争的压力之下,那种田园牧歌式的状态分崩离析了。大量财富积聚了起来,这些财富并没有用来贷款从而赚取利息,而总是重新用于商业投资。从前那种闲适自在的生活态度让位于一种冷酷无情的节俭,一些人在商业活动中就是通过节俭而发家致富的。这些人并不想消费而只想赚取,而另外一些希望保持旧的生活方式的人也不得不削减其消费开支。
这就是韦伯笔下西欧资本主义初期的企业家形象。韦伯甚至神来之笔的描绘了这些人在引领社会前进时所遭受的那些误解和曲解:
……资本主义精神已经开始发生作用了。……但它的出现往往不是一帆风顺的。各种怀疑、仇恨甚至道德义愤总是滔滔不绝地涌向第一个革新者。人们还千篇一律地 ——这类事例我略知几个——捏造出一些关于他从前生活的隐私污点的传说。只有超乎寻常的坚强性格才能使这样一个新型的企业家不至丧失适度的自我控制,才能使他免遭道德上和经济上的毁灭。否认这一事实当然是再容易不过的事情了。而且,只是因为这种新型的企业家具有确定不移且是高度发展的伦理品质,以及洞若观火的远见和行动的能力,他才在顾客和工人中间赢得了不可缺少的信任。没有任何别的东西能够给予他克服重重障碍的力量,更重要的是,没有任何别的东西能够使他承担起近代企业家必须承担的无比繁重的工作。可是这样一些伦理品质却与那些适应传统主义的伦理品质有着天壤之别。
而在日本明治维新时期,这样的阶层是由商人和武士所构成的:
最重要的恐怕要数日本那种独一无二的下层武士和商人的“特殊联盟”,这种联盟即使在封建时代也有滋生的土壤。这些商人曾都是大名雇佣的心腹,亲自经营和管理过各藩的垄断企业,如矿山、纺织、造纸等,在这个过程中,他们政治斗争的技巧得到了磨练并逐渐成熟。然后,这些商人纷纷购买了武士身份。并在武士阶层中普及了生产技术知识。这种武士和商人的联盟迅速把那些自信且干练的人才推上前台,为明治政府的改革出谋划策。不过,问题的关键并不在于他们出身于哪个阶层,而在于他们为什么能变得如此精明、强干和务实?十九世纪后半叶的日本才刚刚脱离中世纪不久,它的国力与今日的泰国差不多,在这种综合实力薄弱的情况下却能产生出这样一批审时度势的领导人实属不易。他们齐心协力、成功地推进了一个最需要政治手腕的改革大事业,这是任何其他的民族都未曾尝试过的。
本尼迪克特写作《菊与刀》时二战刚结束,她可能还未来得及了解中国的情况。中国崛起的领导者——中国共产党,其主要成分是来自社会底层的农民,以及农民出身的军官、知识分子阶层。这些阶层的共同点,即我上面所说的,能超越本集团的利益,放下一时的得失,带动整个族群。
TG在创建新中国的过程中做出了巨大牺牲——无论政党还是军队。建国后,仍然不断有某个阶层为整体发展让渡部分利益的行为——如农民的剪刀差,工人阶级的下岗,现在又轮到城市中产阶级。这些未必是自觉自愿的——谁叫中国不能走向外掠夺的道路——但却是实实在在的。
古今中外,产业升级无不受到既得利益阶层的阻扰。可用的办法无非是战争,革命
Weinberg量子场论阅读笔记 ——写在四读Weinberg I之后
在伟大的相吧发一个。。
Weinberg量子场论阅读笔记
——写在四读Weinberg I之后

一
前些天备考规范场论,顺带着把Weinberg复习了一遍,发现不仅以前熟悉的公式遗忘速度惊人,连前几次读时令我拍案叫绝欲罢不能的思想都已然在脑中模糊不清,于是痛定思痛打算写个笔记。下面的每节是我记下的对Weinberg各章的理解。
二
对称性的意思是事物处在一个状态时测量某种属性结果的概率不依赖于观察者的位置(也即坐标架的选择)。由此Wigner推出对于不同观察者的态之间通过一个幺正或反幺正算符转换。特别地,不同时刻的观察者观察到的态也由一个幺正算符转换。
对称变换算符构成一个射影表示。当对称群被扩大为其覆盖群后,此射影表示可以被还原成非射影表示。
狭义相对论基本公理——所有保持平直、连续的时空坐标变换需满足任意两个事件的时空间隔不变性。
时空平移变换下的概率不变性导致存在相应的变换算符与守恒量:能动量P、角动量J。
单粒子态定义为动量算符的本征值。
由于四动量平方在适当正时洛伦兹变换下不变,具有不同的四动量的粒子态可按其符号分为六类。
同种四动量分类下的粒子依然可以有不同的态。对有正静能的粒子,在其保持动量不变的群(即little group)下变换时,我们将洛伦兹变换后仍是同一组态的线性组合时的这个集合归类为拥有某个自旋的粒子。因为矩阵是群的表示的理想工具,因而我们也将粒子态表示为分量形式,相应的幺正算符即具有矩阵的形式。
对零质量粒子,可以拥有连续本征值的属性,因目前尚未发现此属性,因此所有零质量粒子用运动方向上的角动量(即螺旋度)来分类。如果存在空间反演对称性,则正负同螺旋度的粒子将可以相互转换,从而被归类为一种粒子。由三维旋转群的双连通性质,可以得出自旋必须是整数或半整数。
在不考虑弱作用时,现实存在空间反演对称性,其守恒量称为宇称。
三
自由多粒子态由单粒子态直积得到。
粒子实验中的入态和出态由包含相互作用的完整哈密顿量定义。
将哈密顿量拆成自由场和相互作用场后可以写出从自由场出入态(即动量本征态)导出相互作用场出入态的严格的Lippmann-Schwinger方程。
入态和出态的内积称为S矩阵,对应可定义S算符。代入Lippmann-Schwinger方程可以得到S矩阵的波恩近似。
哈密顿量密度对类空间隔对易的条件以及相互作用势的平滑性条件保证了散射过程的S矩阵的洛伦兹对称性。
同位旋对称性、全局对称性、空间反演对称性都会反映在S矩阵的对称性上,并导致相应守恒量。
从S矩阵可以导出实验上观测的出射粒子动量角分布,即微分散射截面。
S矩阵满足一个微分方程,可以通过微扰展开得到解,所以S矩阵可以写成哈密顿量的时序积分形式。
由S矩阵的幺正性可以得到光学定理、玻尔兹曼H定理、细致平衡条件。
四
出于数学上构造哈密顿量的目的,我们抽象地定义升降算符(谐振子可以为此抽象框架提供一个具体的实现模型,但并不必要,实际上整套量子场论的叙述可以完全脱离谐振子的语境)。升降算符的对易关系由定义和交换对称性(或反对称性)即可得到。
因果性原理要求类空间隔的事件不相互影响,此即S矩阵需满足的集团分解原理(Cluster decomposition principle)。
由于任何哈密顿量均可由升降算符构成的基组合得到,而且当系数满足恰有一个三维动量守恒δ函数时哈密顿量必满足集团分解原理,因此我们喜爱要用升降算符来构造哈密顿量。
因为我们可以直接用粒子数算符乘上单粒子态能量做积分写出自由场(即无相互作用)中的哈密顿量,这就对自由场哈密顿量的形式给出了限制。
我们需要拉格朗日框架的理由是:在拉格朗日框架中能够有效地分析对称性。
作用量泛函的全局对称性导致守恒流算符,其相应荷的全空间积分守恒,此即诺特定理。
五
由于升降算符在洛伦兹变换下有复杂的变换公式,因此一个用升降算符构造标量哈密顿量密度的便捷方法是先将升降算符分别组合成洛伦兹变换公式较为简单的升降场算符(指产生场算符ψ-和湮灭场算符ψ+)。
升降场算符在洛伦兹变换下的性质限制了升降场算符的变换矩阵必须是洛伦兹群的表示,于是我们依照洛伦兹群表示给不同的升降场算符分类。
一组不同的场算符在洛伦兹变换后结果可能是原有算符的线性组合,我们将这样一组场算符归类为同一个场的不同分量。
升降场算符尚且不能直接满足类空间隔对易条件(或反对易条件),一个可行的办法是将升降场算符(ψ-和ψ+)线性组合得到场算符(ψ),场算符则可以满足类空间隔对易条件(或反对易条件)。因此我们通过场算符来方便地构造的哈密顿量密度可以满足类空间隔对易条件。
场算符作用在真空态上得到的态的物理意义是一个在此时空点的粒子,但注意其波函数是延展的,仅仅在非相对论近似下此波函数才是δ函数。
场算符表示的粒子的自旋只能与场算符需要满足的类空间隔对易条件或反对易条件中的一个数学上相容,此即导致了自旋-统计定理。
这样构建的场算符自动满足Klein-Gordon方程。
螺旋度是零质量粒子在运动方向上的角动量,严格的螺旋度概念只对零质量粒子适用。手性是按照场算符属于洛伦兹群的左手表示还是右手表示来定义。对于零质量粒子,左手(右手)螺旋度的粒子对应左手(右手)手性的场算符。
全局对称性导致的荷守恒要求哈密顿量密度与荷算符(Q)对易,这可以通过要求荷算符与场算符对易而达到,这一要求导致对此载荷粒子存在相应的反粒子。
用场算符构造的具有洛伦兹标量哈密顿量密度的理论自动满足CPT定理。
对自旋大于等于1/2的零质量粒子,其场算符数学上不能满足前述的简单的洛伦兹变换公式,而有一个多出项。一个方案是由此场算符(Aμ)构造消去了多出项的反对称张量场算符(Fμν)作为出发点,但这样的理论无法具有长程相互作用。另一个方案是通过设定拉格朗日量密度满足相应的规范对称性来保证S矩阵的洛伦兹不变性,详见第八部分。
类似地,引力子需要满足对应的广义协变对称性以包含长程作用力。由于现实中未发现更高阶的守恒张量,因而高自旋粒子不能具有长程相互作用。
六
S矩阵微扰计算的积分无穷级数公式可以可视化为费曼图。
传播子是公式展开中对应于连接两个顶点的项,计算出来后包含一个非协变的奇异项(起源于时序算符的奇异性),此奇异项会被相互作用哈密顿量中对应的奇异项消除。
S矩阵傅里叶变换后得到的动量空间S矩阵在数学上更便捷。
七
因为标量场算符和其时间导数满足的等时对易关系令人联想起分析力学中相应的对易关系,因此我们类似地定义正则坐标和正则动量算符,证明其满足哈密顿方程,从而建立起场论的哈密顿框架。
根据已知的自由场哈密顿量用升降算符表示的形式,我们可以写出一个用正则变量表示的哈密顿量密度(会有一个真空能的差别)。
通过勒让德变换,我们可以从哈密顿框架转换到拉格朗日框架。
升降算符对易关系、正则坐标算符对易关系、哈密顿方程、拉格朗日方程,四者相互等价,传统讲法则是以拉格朗日方程作为建立量子场论的出发点。
当我们要从自由场转换到相互作用场时,只需在哈密顿框架或拉格朗日框架中自由场的对应量上加上相互作用标量算符项即可。
我们无法直接解出有相互作用的场方程,因此我们转换到相互作用表象中,在此表象中场算符满足自由场中的场方程,从而可以解出。
一个满足平滑条件和洛伦兹不变性的拉格朗日量密度具有的散射过程的S矩阵满足洛伦兹不变性,而构造具有洛伦兹不变性的拉格朗日量密度数学上比较简单,这是我们偏爱朗格朗日框架的原因之一。
拉格朗日量自身的奇异性或者采取特定规范的处理会导致场方程出现奇异性。奇异性可能导致方程不完备或者传统的对易关系与场方程矛盾。相应的解决办法是选定规范条件,采用狄拉克对易子替代原有对易关系。
八
第五章中已提到,对自旋大于等于1/2的零质量粒子,其场算符在洛伦兹变换下有一个多出项,这一项会破坏哈密顿量密度的标量性质,破坏S矩阵的洛伦兹不变性。因为此多出项是一个算符的散度,因此一种可行的解决办法是让此多出项恰好是一个守恒流算符的散度,从而自然等于零,这就导致需要引入一个拥有局域对称性的场,称为规范场。载荷粒子场的局域对称变换和零质量粒子的洛伦兹变换多出项合称为规范变换。运用引入规范场的方法我们最终重新获得了拉格朗日量密度在洛伦兹变换以及规范变换下的不变性。
这样的构建方式以自旋大于等于1/2的零质量粒子对应场算符无法直接构建标量哈密顿量密度为出发点,而传统讲法则是以规范变换作为出发点。
规范不变性导致场方程不完备,解决方法是固定规范。固定规范后传统的对易关系不能被满足,我们使用狄拉克括号的方法修改对易关系。随后即可通过勒让德变换得出哈密顿量,再转入相互作用表象后即可算出传播子,写出费曼规则,量子电动力学模型即建成。
九
由正则变量对易关系可以导出路劲积分公式。如果哈密顿量是正则动量的二次函数,则可积出动量部分得到关于作用量泛函的路劲积分。
通过一系列形式运算可以得出费曼规则和传播子。
对于费米子场,相应正则变量满足反对易关系,因此路劲积分需要的正则变量的本征值也应当满足反对易关系。复数不能满足此关系,因此引入Grassmann代数和其上的微积分。
十
对称性让我们能够得出一些非微扰结论。
考虑圈图对出腿、入腿函数(u*和u)的影响会导致它们与我们最初费曼规则的定义有所不同,对称性分析指出考虑所有非微扰效应后的出腿、入腿函数与最初费曼规则的出腿、入腿函数只相差一个因子(此因子实际上发散),因此我们修改场算符的定义——此即场算符的重整化——来使出腿、入腿函数回归到最初费曼规则的定义(因此算散射过程时外腿上的圈不用计算)。此场算符的重整化体现在自由场算符在升降算符上展开时比原先多了重整化系数,也就是说这个原先可以自由选择的系数现在要被确定。
粒子质量可以自然地采用单粒子态四动量的平方来定义,这个质量与自由场拉格朗日量密度中出现的质量是同一个。当有相互作用时,这套质量的定义方案不易实现,因此我们用考虑所有非微扰效应后的传播子的极点位置来定义。
重整化导致我们重新将用裸场算符写成的拉格朗日量密度作为基本公理,其中的质量、耦合常数也应当是裸质量、裸耦合常数。
理论上我们可以直接使用裸拉格朗日量密度(L)计算散射过程,因为实际上如此计算的总散射过程并没有发散。每一项表观的“发散困难”仅仅是由公式中有无穷大系数的裸场算符、裸质量、裸耦合、以及需要考虑的外腿上的圈、需要考虑的无穷多个图造成的,这个表观的“发散”本质上是源于我们不能直接处理这里的数学困难。
为避开前述的数学困难,我们人为地将裸拉格朗日量密度拆开成两部分(L=L0+L1),第一部分(自由场项)通过将无穷大扔给抵消项的方式而使其导出的传播子不发散,第二部分(包括抵消项和相互作用项)全部被视作相互作用,使用微扰方法计算(因此实际上这个微扰项远比第一部分大;尽管如此,数学却是很奇妙的)。运用这样的数学技巧我们就通过分离不同的无穷大再相互抵消而避开了我们前述的数学上直接处理多个无穷大的困难。
耦合常数随能标的跑动源于耦合常数定义的不同。裸耦合常数具有确定值,而重整化的耦合常数中的重整化系数依赖于其定义所在能标,因此不同能标定义的重整化耦合常数可以联系起来,进而求出相应的β函数。
Ward恒等式是另一个重要的非微扰结论,其来源不过是将n点格林函数与(n-1)点格林函数联系起来。此恒等式的历史价值在于绕开二圈图计算中的重叠发散(overlapping divergence)问题。
电子的“自旋磁矩”这个词有一定误导作用,电子的磁矩确实与自旋有关,因为不同自旋的粒子有其特定的电磁作用顶点。但一般而言,粒子的磁矩和自旋之间没有简单的关系。例如中微子自旋同为二分之一,但磁矩为零。
十一
Pauli-Villars正规化和维数正规化的计算方法都是面向一个目的——定量地处理无穷大计算并让他们相互抵消,因此表征这个无穷大的量具体是什么——截止能量还是维度——并不重要。用能量截止处理无穷大会遇到规范对称性被破坏的麻烦,因此维度正规化更为推荐。
当费曼图中有电子外腿时,即会出现红外发散,这源于外腿电子发射低能光子。
十二
有效场论的概念源于1935年将光子间一圈相互作用近似成电磁场拉格朗日量的高阶项,其数学上等效于在路劲积分中将低能下不会产生的重粒子(在光子相互作用中是正负电子)的场算符预先做积分,最后留下不含重粒子的有效拉格朗日量。
即使是对传统上的不可重整化理论,我们也可以通过在拉格朗日量中添加完整所有满足对称性的项、然后同时调整所有的自由参数来可消去发散。在这个意义下,量子引力理论可能也能够写成量子场论的形式,并且在低能近似下成为有效场论。
有效场论为现实中场论的拉格朗日量密度中只出现可重整项的现象提供了一个可能的(仅仅是可能)解释方法:不可重整项中包含的负能量量纲耦合常数中的能量量纲来自于更高能标的未知粒子,在低能下被压低而致其效应可忽略。
更重要的是,在这样的理解下,写出一个理论的拉格朗日量密度不再是依靠纯粹的猜测或类比经典模型,而是一开始就在拉格朗日量密度中写出所有保证哈密顿量具有有限下界、满足洛伦兹对称性和规范对称性(我们确实不知道为何有规范对称性)的所有可能的项,然后在有效场论的意义下丢掉被压低的所有不可重整项。正是这样的构建方式,解释了为何拉格朗日量、或哈密顿量、或场方程采取了我们如今已经默认了的形式。正是这样的一整套思路,超越了以类比的方式写出场方程作为出发点的大多数量子场论书。
十三
在有内线软光子的圈图中,我们也会遇到红外发散,为解决此问题我们引入界定虚软光子(即内线软光子)三维动量大小的上、下限参数。其中上限参数与圈图计算中的光子动量下限衔接,下限参数用于表征无穷大。
对于实软光子引起的红外发散,我们引入探测器阈值、遗漏能量两个参数。探测器阈值是光子探测器能保证记录事例时的光子能量阈值,遗漏能量是所有未被探测到的光子的能量总和。
上述四个参数中,探测器阈值与遗漏能量参数会真正保留在散射截面的最后结果中,其中令探测器阈值参数趋于零将引起散射截面实质的发散,这是可以直观理解的。而上限参数与圈图计算设定的光子能量下限相抵消,下限参数与实软光子积分中取的下限相抵消。
在量子电动力学中,假设电子静质量为零,则出射态同时有动量平行的电子和软光子会导致红外发散。类似地,量子色动力学中动量平行的强子与软胶子也导致红外发散。这种情况甚至要求散射过程的入态也要受到无红外发散条件的限制。这可以通过我们实验上区分动量平行的零质量粒子时遇到的困难、以及制备动量平行的零质量粒子入态总是呈喷流形态来解释。
仅使用对称性即可证明光散射公式的低能极限只与粒子的质量和电荷有关。
最后一节演示了使用量子场论的工具可推导出经典场论的库伦势。
十四(第一章 历史)
根据狄拉克的回忆,薛定谔在他得到薛定谔方程之前,也在Klein和Gordon之前率先发现了Klein-Gordon方程,但因为Klein-Gordon方程给出了错误的氢原子精细结构而放弃了它,直到几个月后他意识到其非相对论近似得出的薛定谔方程还有一定价值。
狄拉克1928年对描述电子的狄拉克方程的发现及其随后取得的巨大成功有很大巧合的成分:狄拉克寻找一个新方程的动机是解决Klein-Gordon方程的负概率困难,但如今我们清楚负概率问题源于错误地为解赋予概率意义,Klein-Gordon方程本身对于描述零自旋粒子也很有意义。狄拉克通过负质量解预言反粒子存在的方式不仅会引起与负能海相关的一系列问题,而且实质上也仅仅是一个富有启发性的比喻,他不能解释载荷玻色子也有相应反粒子的事实。狄拉克方程预言了正确的电子磁矩的零阶项,但在方程中添加一个Pauli term完全可以将电子磁矩调到任意大小,实际上最终是可重整性限制了量子场论中Pauli term的存在。
结语
一不小心就写了几千字,细想来,读此书或许也排得上整个大学中最重要的几件事了。
我是一个寻求感性理解的人。学习场论的前几年,我都为场论中的词汇感到困惑:什么是升降算符(我以前一直以为升、降算符是一个实际的操作)?谐振子的激发态为什么就是粒子?传播子是什么含义?为什么要把好好的场变成算符?为什么你们的拉格朗日量都长得这么奇怪?二分之一自旋是什么(小学看霍金时就百思不得其解)?维数正规化为什么不是扯蛋?
对这些概念的理解和思考严重地阻碍了我的学习,尤其是当思考的终结点时常停在不可言说的量子态的概念和测量的坍缩问题上时。
如今,有幸能有Weinberg的指点,在几年的沉淀后,我现在也终于能感到量子场论实实在在地站立在一个公理般的基础上,我相信它是这个世界的描述,相信它的构建逻辑,正如本书前言所说:相信它是所有融合了量子力学和狭义相对论的理论在低能近似下必将拥有的形式。
回想2011年秋在天文班自习室初读本书的时候,那时只能看得懂第一章。如今结合了这些全新的理解,更是感慨万千。
第一次做这些计算的前辈,不会如今天的我们这样理解得如此深刻,他们一些人的推理错误百出,甚至觉得这些计算不过是个玩笑。这个场面是如此的似曾相识。即使在贝克莱大主教的批判声中无言以对,整个19世纪的数学家依然建立起了宏伟的分析大厦。即使马赫原理的主旨已不能与后来的广义相对论相吻合,也不可否认爱因斯坦早年从中所汲取的营养。
多年的乱象中总会涌现曲折的前进,逻辑的困难阻挡不住精巧的尝试。人类思维正因这从现象的凌乱中发现模式的能力而愈见其无可比拟。
七星之城
2014年 夏
于北京大学45甲
Weinberg量子场论阅读笔记
——写在四读Weinberg I之后

一
前些天备考规范场论,顺带着把Weinberg复习了一遍,发现不仅以前熟悉的公式遗忘速度惊人,连前几次读时令我拍案叫绝欲罢不能的思想都已然在脑中模糊不清,于是痛定思痛打算写个笔记。下面的每节是我记下的对Weinberg各章的理解。
二
对称性的意思是事物处在一个状态时测量某种属性结果的概率不依赖于观察者的位置(也即坐标架的选择)。由此Wigner推出对于不同观察者的态之间通过一个幺正或反幺正算符转换。特别地,不同时刻的观察者观察到的态也由一个幺正算符转换。
对称变换算符构成一个射影表示。当对称群被扩大为其覆盖群后,此射影表示可以被还原成非射影表示。
狭义相对论基本公理——所有保持平直、连续的时空坐标变换需满足任意两个事件的时空间隔不变性。
时空平移变换下的概率不变性导致存在相应的变换算符与守恒量:能动量P、角动量J。
单粒子态定义为动量算符的本征值。
由于四动量平方在适当正时洛伦兹变换下不变,具有不同的四动量的粒子态可按其符号分为六类。
同种四动量分类下的粒子依然可以有不同的态。对有正静能的粒子,在其保持动量不变的群(即little group)下变换时,我们将洛伦兹变换后仍是同一组态的线性组合时的这个集合归类为拥有某个自旋的粒子。因为矩阵是群的表示的理想工具,因而我们也将粒子态表示为分量形式,相应的幺正算符即具有矩阵的形式。
对零质量粒子,可以拥有连续本征值的属性,因目前尚未发现此属性,因此所有零质量粒子用运动方向上的角动量(即螺旋度)来分类。如果存在空间反演对称性,则正负同螺旋度的粒子将可以相互转换,从而被归类为一种粒子。由三维旋转群的双连通性质,可以得出自旋必须是整数或半整数。
在不考虑弱作用时,现实存在空间反演对称性,其守恒量称为宇称。
三
自由多粒子态由单粒子态直积得到。
粒子实验中的入态和出态由包含相互作用的完整哈密顿量定义。
将哈密顿量拆成自由场和相互作用场后可以写出从自由场出入态(即动量本征态)导出相互作用场出入态的严格的Lippmann-Schwinger方程。
入态和出态的内积称为S矩阵,对应可定义S算符。代入Lippmann-Schwinger方程可以得到S矩阵的波恩近似。
哈密顿量密度对类空间隔对易的条件以及相互作用势的平滑性条件保证了散射过程的S矩阵的洛伦兹对称性。
同位旋对称性、全局对称性、空间反演对称性都会反映在S矩阵的对称性上,并导致相应守恒量。
从S矩阵可以导出实验上观测的出射粒子动量角分布,即微分散射截面。
S矩阵满足一个微分方程,可以通过微扰展开得到解,所以S矩阵可以写成哈密顿量的时序积分形式。
由S矩阵的幺正性可以得到光学定理、玻尔兹曼H定理、细致平衡条件。
四
出于数学上构造哈密顿量的目的,我们抽象地定义升降算符(谐振子可以为此抽象框架提供一个具体的实现模型,但并不必要,实际上整套量子场论的叙述可以完全脱离谐振子的语境)。升降算符的对易关系由定义和交换对称性(或反对称性)即可得到。
因果性原理要求类空间隔的事件不相互影响,此即S矩阵需满足的集团分解原理(Cluster decomposition principle)。
由于任何哈密顿量均可由升降算符构成的基组合得到,而且当系数满足恰有一个三维动量守恒δ函数时哈密顿量必满足集团分解原理,因此我们喜爱要用升降算符来构造哈密顿量。
因为我们可以直接用粒子数算符乘上单粒子态能量做积分写出自由场(即无相互作用)中的哈密顿量,这就对自由场哈密顿量的形式给出了限制。
我们需要拉格朗日框架的理由是:在拉格朗日框架中能够有效地分析对称性。
作用量泛函的全局对称性导致守恒流算符,其相应荷的全空间积分守恒,此即诺特定理。
五
由于升降算符在洛伦兹变换下有复杂的变换公式,因此一个用升降算符构造标量哈密顿量密度的便捷方法是先将升降算符分别组合成洛伦兹变换公式较为简单的升降场算符(指产生场算符ψ-和湮灭场算符ψ+)。
升降场算符在洛伦兹变换下的性质限制了升降场算符的变换矩阵必须是洛伦兹群的表示,于是我们依照洛伦兹群表示给不同的升降场算符分类。
一组不同的场算符在洛伦兹变换后结果可能是原有算符的线性组合,我们将这样一组场算符归类为同一个场的不同分量。
升降场算符尚且不能直接满足类空间隔对易条件(或反对易条件),一个可行的办法是将升降场算符(ψ-和ψ+)线性组合得到场算符(ψ),场算符则可以满足类空间隔对易条件(或反对易条件)。因此我们通过场算符来方便地构造的哈密顿量密度可以满足类空间隔对易条件。
场算符作用在真空态上得到的态的物理意义是一个在此时空点的粒子,但注意其波函数是延展的,仅仅在非相对论近似下此波函数才是δ函数。
场算符表示的粒子的自旋只能与场算符需要满足的类空间隔对易条件或反对易条件中的一个数学上相容,此即导致了自旋-统计定理。
这样构建的场算符自动满足Klein-Gordon方程。
螺旋度是零质量粒子在运动方向上的角动量,严格的螺旋度概念只对零质量粒子适用。手性是按照场算符属于洛伦兹群的左手表示还是右手表示来定义。对于零质量粒子,左手(右手)螺旋度的粒子对应左手(右手)手性的场算符。
全局对称性导致的荷守恒要求哈密顿量密度与荷算符(Q)对易,这可以通过要求荷算符与场算符对易而达到,这一要求导致对此载荷粒子存在相应的反粒子。
用场算符构造的具有洛伦兹标量哈密顿量密度的理论自动满足CPT定理。
对自旋大于等于1/2的零质量粒子,其场算符数学上不能满足前述的简单的洛伦兹变换公式,而有一个多出项。一个方案是由此场算符(Aμ)构造消去了多出项的反对称张量场算符(Fμν)作为出发点,但这样的理论无法具有长程相互作用。另一个方案是通过设定拉格朗日量密度满足相应的规范对称性来保证S矩阵的洛伦兹不变性,详见第八部分。
类似地,引力子需要满足对应的广义协变对称性以包含长程作用力。由于现实中未发现更高阶的守恒张量,因而高自旋粒子不能具有长程相互作用。
六
S矩阵微扰计算的积分无穷级数公式可以可视化为费曼图。
传播子是公式展开中对应于连接两个顶点的项,计算出来后包含一个非协变的奇异项(起源于时序算符的奇异性),此奇异项会被相互作用哈密顿量中对应的奇异项消除。
S矩阵傅里叶变换后得到的动量空间S矩阵在数学上更便捷。
七
因为标量场算符和其时间导数满足的等时对易关系令人联想起分析力学中相应的对易关系,因此我们类似地定义正则坐标和正则动量算符,证明其满足哈密顿方程,从而建立起场论的哈密顿框架。
根据已知的自由场哈密顿量用升降算符表示的形式,我们可以写出一个用正则变量表示的哈密顿量密度(会有一个真空能的差别)。
通过勒让德变换,我们可以从哈密顿框架转换到拉格朗日框架。
升降算符对易关系、正则坐标算符对易关系、哈密顿方程、拉格朗日方程,四者相互等价,传统讲法则是以拉格朗日方程作为建立量子场论的出发点。
当我们要从自由场转换到相互作用场时,只需在哈密顿框架或拉格朗日框架中自由场的对应量上加上相互作用标量算符项即可。
我们无法直接解出有相互作用的场方程,因此我们转换到相互作用表象中,在此表象中场算符满足自由场中的场方程,从而可以解出。
一个满足平滑条件和洛伦兹不变性的拉格朗日量密度具有的散射过程的S矩阵满足洛伦兹不变性,而构造具有洛伦兹不变性的拉格朗日量密度数学上比较简单,这是我们偏爱朗格朗日框架的原因之一。
拉格朗日量自身的奇异性或者采取特定规范的处理会导致场方程出现奇异性。奇异性可能导致方程不完备或者传统的对易关系与场方程矛盾。相应的解决办法是选定规范条件,采用狄拉克对易子替代原有对易关系。
八
第五章中已提到,对自旋大于等于1/2的零质量粒子,其场算符在洛伦兹变换下有一个多出项,这一项会破坏哈密顿量密度的标量性质,破坏S矩阵的洛伦兹不变性。因为此多出项是一个算符的散度,因此一种可行的解决办法是让此多出项恰好是一个守恒流算符的散度,从而自然等于零,这就导致需要引入一个拥有局域对称性的场,称为规范场。载荷粒子场的局域对称变换和零质量粒子的洛伦兹变换多出项合称为规范变换。运用引入规范场的方法我们最终重新获得了拉格朗日量密度在洛伦兹变换以及规范变换下的不变性。
这样的构建方式以自旋大于等于1/2的零质量粒子对应场算符无法直接构建标量哈密顿量密度为出发点,而传统讲法则是以规范变换作为出发点。
规范不变性导致场方程不完备,解决方法是固定规范。固定规范后传统的对易关系不能被满足,我们使用狄拉克括号的方法修改对易关系。随后即可通过勒让德变换得出哈密顿量,再转入相互作用表象后即可算出传播子,写出费曼规则,量子电动力学模型即建成。
九
由正则变量对易关系可以导出路劲积分公式。如果哈密顿量是正则动量的二次函数,则可积出动量部分得到关于作用量泛函的路劲积分。
通过一系列形式运算可以得出费曼规则和传播子。
对于费米子场,相应正则变量满足反对易关系,因此路劲积分需要的正则变量的本征值也应当满足反对易关系。复数不能满足此关系,因此引入Grassmann代数和其上的微积分。
十
对称性让我们能够得出一些非微扰结论。
考虑圈图对出腿、入腿函数(u*和u)的影响会导致它们与我们最初费曼规则的定义有所不同,对称性分析指出考虑所有非微扰效应后的出腿、入腿函数与最初费曼规则的出腿、入腿函数只相差一个因子(此因子实际上发散),因此我们修改场算符的定义——此即场算符的重整化——来使出腿、入腿函数回归到最初费曼规则的定义(因此算散射过程时外腿上的圈不用计算)。此场算符的重整化体现在自由场算符在升降算符上展开时比原先多了重整化系数,也就是说这个原先可以自由选择的系数现在要被确定。
粒子质量可以自然地采用单粒子态四动量的平方来定义,这个质量与自由场拉格朗日量密度中出现的质量是同一个。当有相互作用时,这套质量的定义方案不易实现,因此我们用考虑所有非微扰效应后的传播子的极点位置来定义。
重整化导致我们重新将用裸场算符写成的拉格朗日量密度作为基本公理,其中的质量、耦合常数也应当是裸质量、裸耦合常数。
理论上我们可以直接使用裸拉格朗日量密度(L)计算散射过程,因为实际上如此计算的总散射过程并没有发散。每一项表观的“发散困难”仅仅是由公式中有无穷大系数的裸场算符、裸质量、裸耦合、以及需要考虑的外腿上的圈、需要考虑的无穷多个图造成的,这个表观的“发散”本质上是源于我们不能直接处理这里的数学困难。
为避开前述的数学困难,我们人为地将裸拉格朗日量密度拆开成两部分(L=L0+L1),第一部分(自由场项)通过将无穷大扔给抵消项的方式而使其导出的传播子不发散,第二部分(包括抵消项和相互作用项)全部被视作相互作用,使用微扰方法计算(因此实际上这个微扰项远比第一部分大;尽管如此,数学却是很奇妙的)。运用这样的数学技巧我们就通过分离不同的无穷大再相互抵消而避开了我们前述的数学上直接处理多个无穷大的困难。
耦合常数随能标的跑动源于耦合常数定义的不同。裸耦合常数具有确定值,而重整化的耦合常数中的重整化系数依赖于其定义所在能标,因此不同能标定义的重整化耦合常数可以联系起来,进而求出相应的β函数。
Ward恒等式是另一个重要的非微扰结论,其来源不过是将n点格林函数与(n-1)点格林函数联系起来。此恒等式的历史价值在于绕开二圈图计算中的重叠发散(overlapping divergence)问题。
电子的“自旋磁矩”这个词有一定误导作用,电子的磁矩确实与自旋有关,因为不同自旋的粒子有其特定的电磁作用顶点。但一般而言,粒子的磁矩和自旋之间没有简单的关系。例如中微子自旋同为二分之一,但磁矩为零。
十一
Pauli-Villars正规化和维数正规化的计算方法都是面向一个目的——定量地处理无穷大计算并让他们相互抵消,因此表征这个无穷大的量具体是什么——截止能量还是维度——并不重要。用能量截止处理无穷大会遇到规范对称性被破坏的麻烦,因此维度正规化更为推荐。
当费曼图中有电子外腿时,即会出现红外发散,这源于外腿电子发射低能光子。
十二
有效场论的概念源于1935年将光子间一圈相互作用近似成电磁场拉格朗日量的高阶项,其数学上等效于在路劲积分中将低能下不会产生的重粒子(在光子相互作用中是正负电子)的场算符预先做积分,最后留下不含重粒子的有效拉格朗日量。
即使是对传统上的不可重整化理论,我们也可以通过在拉格朗日量中添加完整所有满足对称性的项、然后同时调整所有的自由参数来可消去发散。在这个意义下,量子引力理论可能也能够写成量子场论的形式,并且在低能近似下成为有效场论。
有效场论为现实中场论的拉格朗日量密度中只出现可重整项的现象提供了一个可能的(仅仅是可能)解释方法:不可重整项中包含的负能量量纲耦合常数中的能量量纲来自于更高能标的未知粒子,在低能下被压低而致其效应可忽略。
更重要的是,在这样的理解下,写出一个理论的拉格朗日量密度不再是依靠纯粹的猜测或类比经典模型,而是一开始就在拉格朗日量密度中写出所有保证哈密顿量具有有限下界、满足洛伦兹对称性和规范对称性(我们确实不知道为何有规范对称性)的所有可能的项,然后在有效场论的意义下丢掉被压低的所有不可重整项。正是这样的构建方式,解释了为何拉格朗日量、或哈密顿量、或场方程采取了我们如今已经默认了的形式。正是这样的一整套思路,超越了以类比的方式写出场方程作为出发点的大多数量子场论书。
十三
在有内线软光子的圈图中,我们也会遇到红外发散,为解决此问题我们引入界定虚软光子(即内线软光子)三维动量大小的上、下限参数。其中上限参数与圈图计算中的光子动量下限衔接,下限参数用于表征无穷大。
对于实软光子引起的红外发散,我们引入探测器阈值、遗漏能量两个参数。探测器阈值是光子探测器能保证记录事例时的光子能量阈值,遗漏能量是所有未被探测到的光子的能量总和。
上述四个参数中,探测器阈值与遗漏能量参数会真正保留在散射截面的最后结果中,其中令探测器阈值参数趋于零将引起散射截面实质的发散,这是可以直观理解的。而上限参数与圈图计算设定的光子能量下限相抵消,下限参数与实软光子积分中取的下限相抵消。
在量子电动力学中,假设电子静质量为零,则出射态同时有动量平行的电子和软光子会导致红外发散。类似地,量子色动力学中动量平行的强子与软胶子也导致红外发散。这种情况甚至要求散射过程的入态也要受到无红外发散条件的限制。这可以通过我们实验上区分动量平行的零质量粒子时遇到的困难、以及制备动量平行的零质量粒子入态总是呈喷流形态来解释。
仅使用对称性即可证明光散射公式的低能极限只与粒子的质量和电荷有关。
最后一节演示了使用量子场论的工具可推导出经典场论的库伦势。
十四(第一章 历史)
根据狄拉克的回忆,薛定谔在他得到薛定谔方程之前,也在Klein和Gordon之前率先发现了Klein-Gordon方程,但因为Klein-Gordon方程给出了错误的氢原子精细结构而放弃了它,直到几个月后他意识到其非相对论近似得出的薛定谔方程还有一定价值。
狄拉克1928年对描述电子的狄拉克方程的发现及其随后取得的巨大成功有很大巧合的成分:狄拉克寻找一个新方程的动机是解决Klein-Gordon方程的负概率困难,但如今我们清楚负概率问题源于错误地为解赋予概率意义,Klein-Gordon方程本身对于描述零自旋粒子也很有意义。狄拉克通过负质量解预言反粒子存在的方式不仅会引起与负能海相关的一系列问题,而且实质上也仅仅是一个富有启发性的比喻,他不能解释载荷玻色子也有相应反粒子的事实。狄拉克方程预言了正确的电子磁矩的零阶项,但在方程中添加一个Pauli term完全可以将电子磁矩调到任意大小,实际上最终是可重整性限制了量子场论中Pauli term的存在。
结语
一不小心就写了几千字,细想来,读此书或许也排得上整个大学中最重要的几件事了。
我是一个寻求感性理解的人。学习场论的前几年,我都为场论中的词汇感到困惑:什么是升降算符(我以前一直以为升、降算符是一个实际的操作)?谐振子的激发态为什么就是粒子?传播子是什么含义?为什么要把好好的场变成算符?为什么你们的拉格朗日量都长得这么奇怪?二分之一自旋是什么(小学看霍金时就百思不得其解)?维数正规化为什么不是扯蛋?
对这些概念的理解和思考严重地阻碍了我的学习,尤其是当思考的终结点时常停在不可言说的量子态的概念和测量的坍缩问题上时。
如今,有幸能有Weinberg的指点,在几年的沉淀后,我现在也终于能感到量子场论实实在在地站立在一个公理般的基础上,我相信它是这个世界的描述,相信它的构建逻辑,正如本书前言所说:相信它是所有融合了量子力学和狭义相对论的理论在低能近似下必将拥有的形式。
回想2011年秋在天文班自习室初读本书的时候,那时只能看得懂第一章。如今结合了这些全新的理解,更是感慨万千。
第一次做这些计算的前辈,不会如今天的我们这样理解得如此深刻,他们一些人的推理错误百出,甚至觉得这些计算不过是个玩笑。这个场面是如此的似曾相识。即使在贝克莱大主教的批判声中无言以对,整个19世纪的数学家依然建立起了宏伟的分析大厦。即使马赫原理的主旨已不能与后来的广义相对论相吻合,也不可否认爱因斯坦早年从中所汲取的营养。
多年的乱象中总会涌现曲折的前进,逻辑的困难阻挡不住精巧的尝试。人类思维正因这从现象的凌乱中发现模式的能力而愈见其无可比拟。
七星之城
2014年 夏
于北京大学45甲
(1)
第二段改动了不少,觉得之前的信息传达的很不确切,改动后如下:
二
对称性的意思是当事物处在一个态时观测其处于另一个态的概率不依赖于观察者的时空位置与运动状态(也即坐标架与惯性系的选择)。由此 Wigner 推出对于不同观察者的态之间通过一个幺正或反幺正算符转换。特别地,不同时刻的观察者观察到的态也由一个幺正算符转换。
狭义相对论基本公理——所有保持平直的时空坐标变换需满足任意两个事件的时空间隔不变性。
我们将洛伦兹对称性导致的幺正算符做小量展开时的一阶项系数标记为H、P、J、K,群所需满足的结合律使得这四个系数算符需要满足一定的关系——实际上是他们之间的对易关系。我们根据这些对易关系而赋予四个算符的物理含义,例如依据 [H,P]=[H,K]=0 我们将 H 命名为能量,依据 [Ji,Jj]=i Jk 而将 J 命名为角动量。
什么是粒子?我们将单粒子态定义为动量算符 P 的本征态。
由于四动量平方(P^2)在适当正时洛伦兹变换下不变,因而具有不同的四动量的粒子态可分为六类。
上述的分类并不完全,因为同种四动量分类下的粒子依然可以有不同的态。继续分类的方法是,对有正静能的粒子,在其保持动量不变的群(即 little group)下变换时,我们将洛伦兹变换后仍是同一组态的线性组合时的这个集合归类为拥有某个自旋的粒子。因为矩阵是群表示的理想工具,因而我们数学上可以将粒子态表示为分量形式,相应的洛伦兹变换算符即具有矩阵的形式。
零质量粒子可能拥有连续本征值的属性,但因目前尚未发现具有此属性的粒子,因此所有已知的零质量粒子只能用运动方向上的角动量(即螺旋度)来分类。如果正负同螺旋度的粒子可以相互转换(例如具有空间反演对称性的电磁相互作用中的光子),从而被归类为一种粒子。由三维旋转群的双连通性质,可以得出自旋必须是整数或半整数。
除开弱相互作用,强相互作用和电磁相互作用都具备空间反演对称性,因而有相应守恒量,此守恒量称为宇称。
二
对称性的意思是当事物处在一个态时观测其处于另一个态的概率不依赖于观察者的时空位置与运动状态(也即坐标架与惯性系的选择)。由此 Wigner 推出对于不同观察者的态之间通过一个幺正或反幺正算符转换。特别地,不同时刻的观察者观察到的态也由一个幺正算符转换。
狭义相对论基本公理——所有保持平直的时空坐标变换需满足任意两个事件的时空间隔不变性。
我们将洛伦兹对称性导致的幺正算符做小量展开时的一阶项系数标记为H、P、J、K,群所需满足的结合律使得这四个系数算符需要满足一定的关系——实际上是他们之间的对易关系。我们根据这些对易关系而赋予四个算符的物理含义,例如依据 [H,P]=[H,K]=0 我们将 H 命名为能量,依据 [Ji,Jj]=i Jk 而将 J 命名为角动量。
什么是粒子?我们将单粒子态定义为动量算符 P 的本征态。
由于四动量平方(P^2)在适当正时洛伦兹变换下不变,因而具有不同的四动量的粒子态可分为六类。
上述的分类并不完全,因为同种四动量分类下的粒子依然可以有不同的态。继续分类的方法是,对有正静能的粒子,在其保持动量不变的群(即 little group)下变换时,我们将洛伦兹变换后仍是同一组态的线性组合时的这个集合归类为拥有某个自旋的粒子。因为矩阵是群表示的理想工具,因而我们数学上可以将粒子态表示为分量形式,相应的洛伦兹变换算符即具有矩阵的形式。
零质量粒子可能拥有连续本征值的属性,但因目前尚未发现具有此属性的粒子,因此所有已知的零质量粒子只能用运动方向上的角动量(即螺旋度)来分类。如果正负同螺旋度的粒子可以相互转换(例如具有空间反演对称性的电磁相互作用中的光子),从而被归类为一种粒子。由三维旋转群的双连通性质,可以得出自旋必须是整数或半整数。
除开弱相互作用,强相互作用和电磁相互作用都具备空间反演对称性,因而有相应守恒量,此守恒量称为宇称。
量子公设的第三条是对测量下的定义。量子测量可以通过一个测量算符的集合
 来表示,它作用在系统的状态空间上。
来表示,它作用在系统的状态空间上。科普量子瞬间传输技术,包你懂!
2015-03-07 23:20
科普量子瞬间传输技术,包你懂!作者:@中科大胡不归
最近有一条消息“中科大潘建伟项目组实现量子瞬间传输技术重大突破”(http://m.guancha.cn/Science/2015_03_06_311259http://m.guancha.cn/Science/2015_03_06_311259),令许多人激动不已,观者如堵。怎么个激动法?最常见的反应有两种。一种是:“你们说的每一个字我都认识,但是你们说的东西我特么一点都听不懂!赞!!”可以简称“不明觉厉”。另一种是:“以后到了公交站,刷卡,选地点,biu的一声就出现在目的地公交站啦!爽!”可以简称“瞬间移动”。其实两种反应都是被小编误导的,因为小编的配图是《星际迷航》中的瞬间传输装置(每次与量子传态有关的报道他们总要配这个),前者可能认真地读了报道,发现根本没法连成一个完整的故事。没办法,懂得科学原理的小编不多,小编能想到的“日常生活”对应物只有这个“beam me up”。是不是很希望专业人士来做个准确的科普? 我的专业是理论物理化学,按说没资格科普量子信息。不过我好歹懂得比公众多一些,并且请教了一位潘建伟院士组里的同事陈博士。虽然陈博士不是这篇文章的作者,而且一再声称他做的不是这一块,对整个量子信息也了解有限(这是科研工作者的标准态度,有一分证据说一分话),但还是提供了很多深入浅出的解读,特此鸣谢。于是乎,我觉得我对这项工作有一定的宏观了解,可以向公众解释解释了。虽然在内行看来很粗浅,但至少可以澄清一些误解,让你明白这项成果实际上是什么,不是什么,在科学史上处于什么位置,重要性有多高。我的叙述会力求简明,让高中以上文化水平的人都能看明白,同时力求准确,给出正确的科学图像。其实准确的表述往往比似是而非的表述更容易理解,这是看了很多半通不通的报道和教材之后的感受。总之,包你懂!如果还是不懂……再看一遍!:-) 这项工作是2月26日以封面标题的形式发表在国际顶级科学期刊《自然》(Nature)上的,文章标题是《单个光子的多个自由度的量子隐形传态》(“Quantum teleportation of multiple degrees of freedom of a single photon”)。这里新的成果是“多个自由度”,因为1997年就实现了单个光子的单个自由度的量子隐形传态。那么,什么是光子?(这个问题大家应该都知道,光子是光的最小单元,日常见到的一束光中包含非常多个光子。)什么是自由度?什么是量子?什么是态?什么是量子传态? 一个物理量如果存在最小的不可分割的基本单位,我们就说这个物理量是量子化的,把这个最小单位称为量子。光子就是光量子,一束光至少包含一个光子,再少就不存在了。实验发现,原子中电子的能量不是连续变化的,而是只能取一些分立的值,也就是说,原子中的电子能量是量子化的。量子化是微观世界的普遍现象。20世纪上半叶(主要是从1900年到1930年),普朗克、爱因斯坦、德布罗意、玻尔、海森堡、薛定谔、狄拉克、玻恩、泡利等伟大的物理学家们创立了量子力学,这是我们目前对微观世界最准确的描述。相对论几乎是爱因斯坦独力创造出来的,量子力学却是群星璀璨的产物。爱因斯坦在其中也发挥了非常重要的作用(提出光量子,这是他得诺贝尔物理学奖的原因,居然不是相对论!),但并不是最重要的,最重要的两个贡献者是普朗克和海森堡。不过上面无论哪一位,都比在世的物理学家伟大多了(杨振宁可能跟泡利相差不是很远?),这是时代的垂青,个人无法改变的。 量子力学描述世界的语言跟经典力学有根本区别。经典力学描述一个粒子的状态,说的是它在什么位置,具有什么动量。不言而喻的是,在任何一个时刻这个粒子总是位于某个位置,具有某个动量,即使你不知道是多少。量子力学描述一个粒子的状态,却是给出一个态函数或者称为态矢量,这个态矢量不是位于日常所见的三维空间,而是位于一个数学抽象的线性空间。在这里我们不需要深究这是个什么空间,关键在于两个态矢量之间可以进行“内积”的运算。内积是什么?在三维空间中,两个长度为1的单位矢量a和b做内积(a, b),得到的是它们夹角的余弦,即两个矢量方向相同时得到1,方向相反时得到-1,互相垂直时得到0,所以内积也可以理解为一个矢量在另一个矢量上的投影。对两个态矢量也可以求这样的内积,结果是个复数(即有实部虚部,不一定是实数),而这个复数的绝对值小于等于1。 好,现在不可思议的新概念来了:对于任何一个物理量P(例如位置、动量),态矢量都可以分为两类,一类具有确定的P,称为P的本征态,P的取值称为这个本征态的本征值;另一类不具有确定的P,称为P的非本征态。非本征态比本征态多得多,如同无理数比有理数多得多。也就是说,绝大多数情况下,一个粒子是没有确定的位置的!等等,什么叫做“没有确定的位置”?是因为粒子跑得太快了,我们看不清吗?量子力学说的不是这种常规(而错误)的理解,而是说:非本征态是一个客观真实的状态,跟本征态同样客观真实,它没有确定的位置是因为它本质上就是如此,而不是因为我们的信息不全。来打个比方,有些状态可以用指向上下左右的箭头来表示,于是你定义“方向”为一个物理量,但是还有些状态是一个圆!圆状态跟箭头状态同样真实,只是没有确定的方向而已。 但是读者还会困惑,因为我们总是可以用仪器去测量粒子的位置,测量的结果总是粒子出现在某个地方,而不是同时出现在两个地方,或者哪里都测量不到。好,下面就是量子力学的关键思想:对P的本征态测量P,粒子的状态不变,测得的是这个本征态的本征值。而对P的非本征态s测量P,会使粒子的状态从s变成某个P的本征态f,概率是s与f的内积的绝对值的平方|(s, f)|^2,发生这个变化后测得的就是f的本征值。用上面的例子来说,对箭头状态测方向,状态不变,得到的就是箭头的方向;对圆状态测方向,圆状态会以相同的几率变成任何一个箭头状态,得到的是这个新的箭头状态的方向。对位置的非本征态测量位置,就会测得粒子出现在某个随机的位置,而出现在空间所有位置的几率之和等于1。怎么知道测量结果是随机的呢?制备多个具有相同状态的粒子,把实验重复多次,就会发现实验结果每次都不一样。没错,量子力学具有本质的随机性,同样的原因可以导致不同的结果,这是跟经典力学的又一大区别。 你也许会觉得上面这些说法简直莫名其妙,但是现在绝大多数科学家都对它们奉若圭臬。为什么呢?因为这套奇怪的理论跟实验符合得很好,而经典力学却不能。当然,这是哲学性的原因,而操作性的原因很简单:现在的科学家受的都是量子力学的教育。普朗克有一句非常有趣的话:“新的科学真理并不是由于说服它的对手取得胜利的,而是由于它的对手死光了,新的一代熟悉它的人成长起来了。”诚哉斯言! 事实上,现在仍然有不少人对量子力学提出各种各样的挑战,包括不少专业科学家,民科就更多了(当然挑战相对论的民科更多)。历史上,挑战量子力学的势力更加强大,其中的带头大哥就是--爱因斯坦!老爱坚信粒子应该具有确定的位置和动量,世界的演化应该是决定性的,对前面说的量子力学的不确定性和随机性十分不满。用他自己的话来说,他相信“没有人看月亮的时候,月亮仍然存在”,以及“上帝不掷骰子”。 如果是一般人,表达完信念也就没事了。但爱因斯坦是超级伟大的科学家,神一样的人物,他不会满足于只做口舌之争,而是要设计一个判决性的实验,以可验证的方式证明量子力学的错误。于是乎,1935年,爱因斯坦(Einstein)、波多尔斯基(Podolsky)和罗森(Rosen)提出了一个思想实验,后人用他们的首字母称为EPR实验。你可以制备两个粒子A和B的“圆”态,使得在这个状态中两个粒子的某个性质(如电子的自旋角动量、光子的偏振)相加等于零,而单个粒子的这个性质不确定。这样一对粒子称为EPR对。然后你把这两个粒子在空间上分开很远,任意的远,然后测量粒子A的这个性质。好比你测得A是“上”,那么你就立刻知道了B现在是“下”。问题是,既然A和B已经离得非常远了,B是怎么知道A发生了变化,然后发生相应的变化的?EPR认为A和B之间出现了“鬼魅般的超距作用”,信息传递的速度超过光速,违反相对论。所以,量子力学肯定有错误。 这个问题非常深邃,直到现在都不断给人以启发。不过量子力学的正统卫道士有一个标准回答:处于“圆”态的A和B是一个整体,当你对A进行测量的时候,A和B是同时发生变化的,并不是A变了之后传一个信息给B,B再变化,所以这里没有信息的传递,不违反相对论。这个回答怎么样?无论你信不信,反正我信了。不过爱因斯坦一直都不信,以这个他参与创建的理论的反对者的身份走完了一生。 在爱因斯坦的时代,EPR实验只能在头脑中进行。随着科技的进步,这个实验可以实现了。1980年代,阿斯佩克特等人做了EPR实验,结果你猜怎么着?完全跟量子力学的预言符合!真的是你测得一个EPR对中的A是“上”的时候,B就变成了“下”。本来是设计出来否定量子力学的,反而验证了量子力学的正确性。这种事在科学史上屡见不鲜。17世纪的时候,牛顿主张光是粒子,惠更斯主张光是波动。牛顿按照惠更斯的理论计算出一个现象:把一束光射向一个不透明的小圆片,在圆片的背后中心位置会出现一个亮点,而不是暗点。牛顿认为这是不可能的,宣布驳倒了惠更斯。可是别人一做这个实验,发现真的就是如此,结果成了牛顿亲手证明惠更斯的正确。这正应了尼采的话:“杀不死我的,使我更强大!” EPR现象既然是一个真实的效应,而不是爱因斯坦等人以为的悖论,人们就想到利用它。量子隐形传态(quantum teleportation)就是一个重要的应用。英文单词teleportation就是科幻艺术中biu的一声把人传过去的瞬间传输,tele是远,port是传,所以小编们报道这种新闻总是配传人的图片,《星际迷航》中的Spock发来贺电!可是,在量子信息研究中实际做的是把一个粒子A的量子态传输给远处的另一个粒子B,让B复制A的状态,注意传的是状态而不是粒子。当然你可以说传人也是把人的所有原子的状态传到远处的另外一堆原子上,组合成一个同样的人。OK我没意见,只不过为了避免混淆,中国的科学家们还是小心谨慎地把teleportation翻译成了隐形传态。 量子隐形传态是怎么操作的呢?基本思路是这样:让第三个粒子C跟B组成EPR对,而C跟A离得很近,跟B离得很远。让A按照某个密码跟C发生相互作用,改变C的状态,于是B的状态也发生了相应的变化。再通过经典的通讯手段(比如电话、光缆)把密码告诉B那边的人,对B按照密码进行反向操作,就得到了A的状态。这里的基本元素包括作为中介的C、密码和传输密码的经典信道。 量子隐形传态是在什么时候实现的?答案是1997年,当时潘建伟在奥地利维也纳大学的塞林格(Zeilinger)教授组里读博士,他们在《自然》上发表了一篇题为《实验量子隐形传态》(“Experimental quantum teleportation”)的文章,潘建伟是第二作者。这篇文章后来入选了《自然》杂志的“百年物理学21篇经典论文”,跟它并列的包括伦琴发现X射线、爱因斯坦建立相对论、沃森和克里克发现DNA双螺旋结构等等,这个阵容强大得吓死人。当然,量子隐形传态的重要性不能和那些神级成果相提并论,不过也已经相当了不起了,尤其是在基础科学已经很久没有革命的当代。 现在终于可以说到潘建伟研究组最新的这个工作了。1997年实现的是单个光子的单个自由度的量子隐形传态,现在实现的是单个光子的多个自由度的量子隐形传态。自由度是什么?自由度就是描述一个体系所需的变量的数目。例如一个静止在一条线上的粒子,描述它只需要一个数,自由度就是1。静止在一个面上的粒子,自由度就是2。三维空间中的静止粒子,自由度就是3。描述三维空间中一个运动的粒子,需要知道位置的3个分量和动量的3个分离,自由度是6。光子具有自旋角动量和轨道角动量,如果你看不懂这两个词,没关系,只要明白它们是两个自由度就够了。在以前的实验中,传的只是轨道角动量的状态。但是如果你想真正传输一个光子的完整状态,应该把这两个自由度的状态都传过去。潘建伟研究组实现的就是这件事。所以完整意义的量子隐形传态,应该说是2015年才实现的。 这两个实验之间为什么隔了18年之久呢?因为前面说的全都是理论,而在实验操作中有非常多的技术困难。为了解决这些困难,他们“巧妙地设计了利用单光子非破坏测量技术实现自旋和轨道角动量多自由度贝尔态测量的新方案,制备了国际上最高亮度的自旋-轨道角动量超纠缠源、高效率的轨道角动量测量器件,搭建了6光子11量子比特的自旋-轨道角动量纠缠实验平台”。不要问我这些是什么意思,对量子信息的业外人士来说这些是技术细节了。重要的是,这些技术进步都非常新颖,非常困难,通过这些实验手段的创新,他们终于达到了多自由度隐形传态的目的。其实这个目的实现得还不是非常完美。文章摘要里有一句“传输的保真度(fidelity)位于0.57至0.68之间”,也就是说,有40%左右的可能性传输失败!这是实验中的种种噪声、损耗造成的,不是理论的限制,以后可以继续提高。在单自由度的传态中,保真度已经能达到99%以上了。这是现代科研的常态,在一个看似简单的故事下面隐含着无数的技术细节。这是隔行如隔山的来源,也是民科在当代的作用远远比历史上小的原因。 知道了这项成果是什么,我们可以来回答它不是什么了。很遗憾,它不是biu的一声把人传走。当然,可以说是朝这个方向前进了一步,而且是一大步。多大的一步?如果用《老子》的话:“道生一,一生二,二生三,三生万物。”1997年是实现了道生一,这次是实现了一生二。不过,离传人有多远的距离呢?可以这样估算。12克碳原子是1摩尔,即6*10^23个。人的体重如果是60公斤,就大约有5000摩尔的原子,即3*10^27个。描述一个原子的状态,我不知道要多少个自由度,姑且算作10个吧。那么要描述一个人,就需要10^28量级的自由度。我们现在刚刚从1进步到了2……就连这个2也不是非常稳定的,还有40%的几率传错,想想如果你身上1%的细胞出了错会怎么样?所以,嗯,我们的征途是星辰大海!骚年,向着夕阳奔跑吧! 由于这项工作的重要性,《自然》在同一期上评论道:“该实验为理解和展示量子物理的一个最深远和最令人费解的预言迈出了重要的一步,并可以作为未来量子网络的一个强大的基本单元。”这是一个恰如其分的评价。如果你要问,能不能得诺贝尔奖?我不好说,不过如果真有一天得奖,塞林格应该在前面,因为道生一肯定比一生二重要。当然,潘建伟和他的团队都还很年轻,他们有无限的可能性,将来因为其它的成就得诺贝尔奖也未可知。科学最大的魅力之一,就是一切皆有可能。(来,干了这碗鸡汤!) 潘建伟研究组是量子信息的世界领导者之一,当然不好说是最先进的,因为在欧洲、美国也有跟他们差不多水平、各有千秋的研究组。在量子保密通信这个领域他们做得尤其突出,创造了多项传输距离的世界纪录,已经有多个政务网投入实用,并将在2016年发射量子卫星。目前中国很少有领域具有这样领先的世界地位,弥足珍贵。 值得特别强调的是,中国的量子信息绝不是一花独放,而是百花争春。仅仅在科大,比较大的研究组就有潘建伟院士、郭光灿院士、杜江峰教授三家,比较小的我就数不过来了。顺便说一下,最近杜江峰研究组在3月6日的《科学》杂志上发表了题为《日常环境下单蛋白质的自旋共振谱》(“Single-protein spin resonance spectroscopy under ambient conditions”)的文章,周荣斌研究组在1月15日的《细胞》(Cell)杂志上发表了题为“Dopamine controls systemic inflammation through inhibition of NLRP3 inflammasome”的文章。在2015年的前3个月,科大在《自然》、《科学》和《细胞》这三大国际顶级期刊(合称CNS)上各发了一篇,堪称开门红。当然,对CNS大惊小怪仍然是中国的大学科研水平有限的证据,因为还是少嘛。什么时候CNS多得大家都不当回事了,不再关心文章发在什么地方,只专注成果的科学重要性,那就真的是世界一流大学了。 据我了解,中国的量子信息研究是从1990年代开始的。那时郭光灿从量子光学转向量子信息,迎来了事业的高峰。潘建伟那时只是研究生,现在已经是国际领军人物了。从这些轨迹可以看出,一个国家的科学可以进步得有多快。1999年左右,杨振宁到科大演讲《近代科学进入中国的回顾与前瞻》,结论是:“以下的几个长远的因素是使得一个社会、一个国家能够有辉煌的科技发展的必要条件。第一个是需要有聪明的年轻人,有头脑做科学研究;第二是需要有重视纪律、重视忍耐心、重视勤奋的社会传统;第三要有决心;第四要有经济条件。……中国在20世纪里有前三者,到了21世纪我认为将四者具备,所以我对21世纪中国科技的发展是绝对乐观的。”当时我十分不以为然,因为中国有太多的问题,腐败,专制,贫富差距,世风日下……所以,杨先生,您是不是老糊涂了?不错,当时我倾向于崩溃论,对中国的前途十分悲观。后来随着眼界的扩大,越来越发现杨振宁讲的是完全正确的。虽然他这些道理看起来无比的质朴,简直是土得掉渣,但实际上是“重剑无锋,大巧不工”。科学大师关于科学发展的眼光确实比我们高得多,不服不行。你说中国没人才,耐心培养不就是了?以中国人的天分,说不定一搞就搞出个国际领导者来。科学最大的魅力之一,就是一切皆有可能。(来,再干了这碗鸡汤!) 在这里我要讲一个故事。美国物理学家拉比(1898-1988)年轻的时候去欧洲留学,发现美国的物理杂志《物理评论》是被一年一次用船运过去的,说明在欧洲科学界看来美国的物理学根本不值得重视。拉比暗下决心振兴美国物理学,回国后担任了《物理评论》的主编,如今这本杂志是世界物理学界最著名的期刊之一,美国的物理学是世界上最先进的。美国化学家鲍林(1901-1994)也是在去欧洲留学之后,把美国的化学提升到了世界最先进水平。 如果当时有“冷静党”跳出来说美国人不行,永远赶不上欧洲,也能找到无数的证据。而这样的“冷静党”在中国一抓一大把,正如@吏部尚书吉哈克 所说:“中国人的意识已经跟不上中国的发展了。国家顶尖的科研人员已经搞的是人类科学中顶尖的那些东西了,而民众甚至人大委员却还在迷恋日本的马桶圈和电饭煲……脚用30年走了人家300年的路,脑子却留在了30年前……” 你愿意向顶尖的科研人员看齐吗?中国最大的魅力之一,就是一切皆有可能。Make it easy: 历史求和 及 拓扑量子场论2013年07月07日 14:45:32
一些参考文献见 wikipedia Topological quantum field theory 条目。
另外,给一些适合数学系看的文章
1 C.Teleman, Five lectures on topological field theory
2 D.S.Freed, Lectures on topological field theory.
3 M.Atiyah, topological quantum field theories, 1989.
4 P.Van Baal, An introduction to topological Yang-Mills theory,1990.
拓扑量子场论的核心就是对于路径积分(历史求和)的数学结构和可能的应用的探索。
对于数学系的学生,最难的地方在于理解路径积分所隐含的代数结构,理解量子物理的数学结构,最关键的一点就是理解路径积分。
历史求和又称路径积分,是量子物理中计算转移振幅的核心方法。本文将强调历史求和和纤维积分(fibre integration),反转映射(Umkehr map),基森映射(Gysin map),傅里叶变换以及Kan extension等常见的重要概念的一致性。
量子物理的核心要素是量子态和量子态之间的关联振幅。历史求和是确定量子态之间的动力学关联强度(转移振幅)的核心方法。系统的量子态总是生活在希尔伯特空间之中,给定系统的动力学,用路径积分的方法可以计算不同时刻不同量子态之间的动力学关联振幅。
首先我们要先明确和区分一些基本的物理概念:
经典位形空间-----------场或者物理对象所有可能的位形状态的集合
经典的态空间---------场或者物理对象所有可能的运动学状态的集合,不仅包括位形还包含动量的信息
量子的态空间---------经典位形空间上的波函数全体构成的希尔伯特空间
讨论经典力学合适的范畴是集合或者流形的范畴
讨论量子力学合适的范畴是希尔伯特空间的范畴
在集合范畴和线性空间范畴有对伴随函子:自由向量空间函子和忘却函子,
自由向量空间函子把一个集合变为这个集合中的元素自由生成的向量空间。
在态空间的层次上,量子化或者说从经典到量子的过程类似于这个自由向量空间函子,量子态空间相当于经典位形空间自由生成的向量空间。所以说经典的状态其实对应的是量子态空间的一组基。
上面说的三个空间都是在某一个确定时刻,系统的可能状态或者位形的全部可能性,现在我们说说和时间段有关的概念
历史空间--------给定两个时刻t_1 和 t_2,任意两个分别在两个时刻的经典态X_1和X_2,任意一个可能的从X_1到X_2过程(或者说路径)都是历史空间的一个元素,用H(t_1,t_2)表示所有从时刻t_1到t_2的历史,这个空间有一个双纤维化结构(bi-fibration structure),记C(t_1)和C(t_2)表示两个时刻的状态空间(可以不一样)。
C(t_1)<---------H(t_1,t_2)---------->C(t_2)
向左这个箭头表示取 过程的起点,向右的箭头表示取过程的终点,这两个箭头都是纤维化。
上面这个图是数学中非常重要,非常常见的图,我们叫它 屋顶(roof),如果把中间的H画的高一点这个名字还是蛮恰当的。其实它有一个更专业的名字:span(参看nLab span 词条)。在这个图中如果把箭头都反过来,我们叫做cospan。这个图的重要性在于表达了两个集合之间二元关系的推广,几乎所有的对偶性和等价性的背后都有这么一个图像。比如傅里叶变换,朗兰兹对偶,森田等价等等。
如果把其中的一个箭头反过来,就是我们熟悉的可以复合两个函数的图像。但是span的箭头有一个方向不对,所以不能符合,但是span和span之间可以符合(做纤维积)。
在上面这个例子中,两个态之间的历史就刚好是这两个态的公共纤维,对这个纤维积分,得到的数就是两个态之间的关联振幅。所以历史求和或者路径积分的数学结构本质上是纤维积分。其实我们按照刚才自由向量空间的说法,我们可以把C(t_1)和C(t_2)中的元素作为指标比如用i,j 表示,历史空间中的公共纤维就可以用i,j标记,i和j的公共纤维记为P(i,j)(path or process)我们可以把这些纤维排成一个“矩阵”,对这个“矩阵”中的各个元素积分就得到一个真正的矩阵(我们还没有说这些纤维上有什么积分测度,我们后面再讲这些,先假设存在一个积分测度),我们记为S(t_1,t_2)这个矩阵就是传说中的S矩阵(S矩阵是量子物理的主要的也是最基本的观察量,S矩阵的系数叫做关联函数,共形场论中的S矩阵和黎曼面模空间上的conformal block,高斯-马宁联络也是有关的,这些S矩阵实际上构成一个Hopf algebra,这些都是后话)。所以量子化在态空间的层次上就是自由向量空间函子,在历史空间的层次上就是双纤维化+纤维积分。因为积分运算是线性算子所以这两个层次的操作是一致的。另外从上面的过程我们可以大致体验到categorical quantum field theory 就是S矩阵(Dyson-Schwinger formalism)的范畴化表述。
现在我们考虑三个相继时刻的情形。考虑三个相继时刻t_1,t_2,t_3, 对应的三个状态空间为C(t_1),C(t_2),C(t_3),其中的元素分别用i,j,k指标标记,这个时候我们有三个历史空间H(t_1),H(t_2),H(t_3),我们还有三个span(历史空间的双纤维化结构)
C(t_1)<------H(t_1,t_2)------->C(t_2),
C(t_2)<-------H(t_2,t_3)-------->C(t_3)
以及
C(t_1)<-------H(t_1,t_3)-------->C(t_3)
和前面的分析类似,由这三个span 我们可以得到三个散射矩阵S(t_1,t_2),S(t_2,t_3)和S(t_1,t_3)。
那么现在一个自然的问题就是所有的这些数据之间的关系是什么?
答案是H(t_1,t_2)和H(t_2,t_3)的关于C(t_2)纤维积(fiber producnt or pull back)刚好是H(t_1,t_3). 我们用span的语言来形式化这个结果就是前两个相继地span的复合是第三个span,这个不需要任何别的假设,只需要你承认我们的世界在时间的流逝下不会出现矛盾,就会自然的得到这个结果。学习这些东西其实不需要太多的数学和物理背景,真正本质的东西都是很简单很自然的。
我把上面的过程在解释一下,考虑t_1和t_3时刻的态i和k,他们之间的历史P(i,k)具有什么样的结构?如果我们在中间时刻t_2做一个观察,可以发现从i到k的过程可以根据在t_2时刻所经历的状态来划分,也就是说P(i,k)这个集合是所有的形如P(i,j)和P(j,k)的笛卡尔积 这样的集合的无交并(j取遍所有C(t_2)的元素)。现在我们开始做纤维积分,P(i,k)得到的积分是矩阵S(t_1,t_3)的i,k分量s_{ik},但是上面说到P(i,k)是一系列笛卡尔积的无交并,在笛卡尔积上做积分我们有富比尼定理(化重积分为累次积分),笛卡尔积P(i,j)P(j,k)的积分就是s_{ij}s_{jk},而在无交并空间上的积分就等于在各个子空间积分的和,
所以 我们得到s_{ik}=\sum_j s_{ij}s_{jk},这恰恰是矩阵乘积的公式,
所以S(t_1,t_3)=S(t_2,t_3)S(t_1,t_2).
在上面的证明中我忽略一些细节,就是历史空间上的测度问题。
其实要注意到量子场论的局部性对于上面的证明是非常要紧的,也就是说历史求和(路径积分)之所以有如此好的代数性质,关键的一条就是作用量的局部性。那么局部性到底什么意思呢?
局部性是指作用量对于过程的可加性(作用量对于时空是广延量)。也就是一个过程的作用量是它的各段中间过程的作用量的和。如果作用量是拉格朗日密度在时空上的积分的话,可加性自然成立。更精确一点,如果过程X=AB(A过程和B过程的复合),那么作用量S(X)=S(AB)=S(A)+S(B).
在做路径积分的时候,作用量是在指数上,所以exp^{S(X)}=exp^{S(A)}exp^{S(B)},
这一个性质保证了历史空间的乘积的测度等于历史空间测度的乘积。
强调一点: 作用量的可加性或者局部性是历史求和具有好的代数结构的先决条件。
一切都非常完美!
on shell-----------------我们上面介绍的东西其实都是在没有物理的一般情况的setting。这里物理指的就是作用量和历史空间上的测度。稍微懂点物理的都知道作用量是历史空间上的函数(通常叫做泛函,因为实际的例子中历史空间都是无限维的)。如果这个系统的物理不是很坏(nondegenerate),作用量实际上是一个莫尔斯函数。on shell 就是历史空间上作用量的极值点,它的物理意义就是经典的可以真实发生的过程(最小作用量原理)。微扰量子场论就是对on shell 进行形变量子化。如果假设作用量非退化,on shell 上会有一个自然的辛结构,这个辛结构是从作用量继承来的,基本上只要有非退化的变分结构,on shell 上都会有辛结构。如果退化我们只能得到预辛结构(pre-sympletic structure)。
通常遇到的例子,它们的状态空间都是同一个也就是和时间没有关系,而且由于on shell 是系统欧拉-拉格朗日方程的解空间,由于微分方程初值问题解的唯一性,所以可以把历史空间的on shell 部分和状态空间等同起来。
off shell-----------------历史空间上不在on shell上的点成为off shell, on shell 上的点都是可以真实发生的,或者满足物理约束的,比如它们满足能量守恒,动量守恒等等,但是off shell上的点不满足物理的限制,但是量子场论中要求off shell 的过程也会对真实的过程产生贡献(路径积分就是 对off shell的量子涨落进行累积),这些off shell 过程通常叫做虚过程,中间涉及的场的激发态叫做虚粒子。量子场论和凝聚态中对粒子的定义为场或者体系的具有一定稳定的特性的激发态,这些激发态通常是是场或者体系在某些相或者量子序下的低级激发态或者基态。
------------------------------------------------------------------------------
这一部分我们来回答以下一些问题。
拓扑量子场论中的拓扑到底意味着什么? 为什么要研究拓扑量子场论?拓扑量子场论又有现实的物理意义?
首先这些答案没有标准答案,数学家和物理学家的答案也不一样。
量子场论的主要的观察量就是散射矩阵或者叫S-matrix,当然如果是多个粒子到多个粒子的散射过程,这个矩阵实际上是一个高阶张量,当然高阶张量和张量空间之间的线性映射是一样。所以我们就不在精细的区分术语。散射矩阵的各个分量或者系数称为散射振幅或者转移振幅,通常物理学家把它们打包成生成函数,叫做所谓的关联函数。 除了一系列的散射矩阵之外,其他的一些主要要观测量就是一些算子的本征值本征态问题,即谱问题,还有系统的各种特殊态的对称性,能谱的研究。那么拓扑场论中的拓扑是什么意思呢?答案就是 拓扑的意思就是散射矩阵是拓扑不变量,或者说关联函数的系数或者散射矩阵的系数都是拓扑数。这是从数学的角度来说,从物理的角度就是,在拓扑场论中所有的粒子都是没有质量的,或者说有效质量为零。这一点和共形场论是一致的。拓扑场论和共形场论中的粒子都是没还有质量的,因为质量的定义是时空对称群的生成元的本征值,如果我们的理论和时空度规没有关系,那就是说是时空对称群的平凡表示,所以就不存在质量。更一般的判断拓扑性的方法(物理学家定义拓扑场论的方法)是看关联函数关于时空度规的变分是否为零,这一点比较接近S矩阵是拓扑不变量的解释。关联函数是拓扑的这个事情的物理图像是什么呢?
考虑时空上两个点或者多个点上发生了一些量子事件,或者说量子场在时空的一些点处出现一些激发或者退激,这些量子事件通常被说成是在这些点处插入顶点算子,这些顶点算子诱导了量子场的激发和退激,物理上要考虑这些量子事件的关联,也就是说这些事件背后有没有什么物理的或者动力学的原因,计算的结果就是关联函数。所以说关联函数是时空坐标的函数(顶点算子实际上是场位形坐标或者场动量坐标的量子化,物理学家通常看做是时空上的delta函数或者场的位形空间上的delta函数)。现在的问题,如果我连续的改变(当然要保证算子之间的时序结构不变)这些顶点算子在时空上插入的位置,关联函数会有什么变化? 答案是如果是拓扑场论的话,关联函数不会改变。那么为什么可以用对时空度规的变分为零来刻画关联函数的拓扑性呢? 这里涉及到主动和被动的描述的问题,改变顶点算子的位置可以等效的认为我改变了时空度规。或者说我可以通过一个微分同胚来实现顶点算子的位移,这个微分同胚可以诱导一个新的度规(比如可以通过pull back),顶点算子在原来的位置上的关联函数如果何在这个新的度规上的定点算子的关联函数是一样的话,那就必须对这个量子系统有一定的限制。这样的限制在共形场论中称为Ward恒等式。这个说法和改变顶点算子的位置而让关联函数不变是一样的。这个不变性不是必然要满足(不是逻辑必然的),如果要满足就说明这个系统是要受到约束的。
从上面的讨论我们也可以看出,相比较于经典场论,量子场论更像是一个黑箱子或者一台机器或者一块材料,为了了解量子场论的结构,我们给它一些刺激,看看它如何反映。这里的刺激就是我们在时空中插入一些顶点算子,来测量一些关联函数,通过这些关联函数我们来反推这个系统应该具有的结构。所以关联函数更像是控制系统的响应函数,知道了足够多的响应函数,我们基本上就了解了这个系统的行为模式。
说明这个事情一个比较好的例子就是黎曼流形上的hodge理论,有了黎曼度量之后我们可以定义调和形式,调和形式的空间和德拉姆上同调空间作为线性空间是同构的(不是作为弗洛比纽斯代数或者结合代数,调和形式上没有外积)。当我们改变黎曼度规的时候,调和形式空间会在微分形式空间转动和伸缩,但是调和形式空间的维数是不会变的,都等于Bitti numbers,说明他们是拓扑不变量。这个Hodge理论被威腾解释成一个超对称的量子力学,这个量子力学的波函数就是复值的微分形式全体(也可以考虑完备化的版本)
-------------------------------------------------------------------------------
1989年,M.Atiyha 受到Segal 公理化定义共形场论的方法的启发,给出了范畴化版本的拓扑量子场论的定义,指出了历史求和 与 流形的协边范畴的关联,揭示了量子场论的内在的数学结构。
拓扑量子场论的主要想法就是把时空解释成空间的定向协边。
时空=空间的定向协边
先解释一下什么是定向协边范畴。我们固定一个维数k,讨论k+1维定向协边范畴,k是空间维数,1表示时间维数。
这个范畴的对象是k维定向(闭)流形,比如M,我们+M和-M表示M的两个定向,它的物理意义就是量子场所生活的空间。两个定向相容的流形-M_1和+N_2(两个对象)之间的协边(协边范畴的态射)是一个k+1维定向流形L(定向反映的是时间方向),这个流形的定向要满足它在拓扑边界上诱导的定向是和M的定向相反和N的定向相同(统一用右手法则定义边界的诱导定向)。
我们可以把这个定向协边简单的写为
L=[-M]----->[+N],
中间的箭头表示时间的方向,L定义域-M表示的是过去的空间,+N表示未来的空间,因为时间是有确定方向的,所以在讨论两个k维闭流形之间的协边的时候 只需要给定L的定向那么定义域和值域的定向就自然确定了,也就是定义域的定向总是和诱导定向相反,值域的定向总是和诱导定向相同。
所有上面的协边可以更加简化为
L=M---->N 而不会引起歧义。
那么定向有什么物理意义呢?实际上,可以这样理解:
协边的定义域上生活的量子态对应于反粒子的激发态,协边的值域上生活的量子态对应于激发态,这是因为费曼把反粒子解释为沿反时间方向运动的粒子,把粒子解释为沿时间方向运动的粒子。这里正反的粒子的区分类似于 狄拉克的刀态(bra)和刃态(ket)的关系,说的更数学些就是 线性空间中的向量和其对偶空间 中的向量的关系。 当然更深刻的解释和CPT定理之类的物理有关,我们不必涉及这么复杂。
如果感觉协边的定向比较绕的话可以先不管这个东西。反正定向协边就是时空演化图,是量子场相互作用的舞台。和普通映射的复合一样,如果一个定向协边L_1的值域的定向和另一个定向协边L_2的值域有相同的定向,我们可以把L_1的值域和L_2的定义域等同起来而得到一个新的定向协边L,这个构造在拓扑上叫做空间的粘贴,在我们这里则把这个操作叫做定向协边的复合记做L=L_2L_1,这个复合和映射的复合满足相同的规律,即存在单位,满足结合律等等。其实这些规律是保证时空的因果结构所必须的。
阿提亚的伟大创见就在于发现时空的演化图(定向协边)和 量子物理中的 历史求和是相容的,换句话说 时空演化的代数结构(定向协边范畴)和量子场的转移振幅所满足的代数结构是一致的或者说 我们可以把定向协边看做是量子场的高维的 费曼图。 所以阿提亚把拓扑量子场论定义为定向协边范畴的线性表示。在粒子物理中,我们可以把量子场论定义为费曼图的表示,从费曼规则的意义上,阿提亚的拓扑量子场论是量子场论中费曼规则的高维推广或者说的更物理一些就是膜(相互作用)的费曼图。
一些简单的类比:
量子力学--------李群/李代数的表示
产生湮灭算子---------李代数的三角分解
(微扰)量子场论----------费曼图的表示
阿提亚的拓扑量子场论----------流形协边范畴的表示
总结一点: 阿提亚的拓扑量子场论是高维膜的量子场论。
下面我们讨论两类模型,来看看为什么历史求和会有如此好的代数结构。限于表达的限制,我只是提炼一些要点,详细的推导在推荐的材料里都有,很详细,很容易follow。
一类是规范模型,一类是sigma模型,这两类模型都可以看做是广义的上同调模型,区别于通常的广义上同调,拓扑量子场论是乘法的,而通常的广义上同调都是加法的。

另外,给一些适合数学系看的文章
1 C.Teleman, Five lectures on topological field theory
2 D.S.Freed, Lectures on topological field theory.
3 M.Atiyah, topological quantum field theories, 1989.
4 P.Van Baal, An introduction to topological Yang-Mills theory,1990.
拓扑量子场论的核心就是对于路径积分(历史求和)的数学结构和可能的应用的探索。
对于数学系的学生,最难的地方在于理解路径积分所隐含的代数结构,理解量子物理的数学结构,最关键的一点就是理解路径积分。
历史求和又称路径积分,是量子物理中计算转移振幅的核心方法。本文将强调历史求和和纤维积分(fibre integration),反转映射(Umkehr map),基森映射(Gysin map),傅里叶变换以及Kan extension等常见的重要概念的一致性。
量子物理的核心要素是量子态和量子态之间的关联振幅。历史求和是确定量子态之间的动力学关联强度(转移振幅)的核心方法。系统的量子态总是生活在希尔伯特空间之中,给定系统的动力学,用路径积分的方法可以计算不同时刻不同量子态之间的动力学关联振幅。
首先我们要先明确和区分一些基本的物理概念:
经典位形空间-----------场或者物理对象所有可能的位形状态的集合
经典的态空间---------场或者物理对象所有可能的运动学状态的集合,不仅包括位形还包含动量的信息
量子的态空间---------经典位形空间上的波函数全体构成的希尔伯特空间
讨论经典力学合适的范畴是集合或者流形的范畴
讨论量子力学合适的范畴是希尔伯特空间的范畴
在集合范畴和线性空间范畴有对伴随函子:自由向量空间函子和忘却函子,
自由向量空间函子把一个集合变为这个集合中的元素自由生成的向量空间。
在态空间的层次上,量子化或者说从经典到量子的过程类似于这个自由向量空间函子,量子态空间相当于经典位形空间自由生成的向量空间。所以说经典的状态其实对应的是量子态空间的一组基。
上面说的三个空间都是在某一个确定时刻,系统的可能状态或者位形的全部可能性,现在我们说说和时间段有关的概念
历史空间--------给定两个时刻t_1 和 t_2,任意两个分别在两个时刻的经典态X_1和X_2,任意一个可能的从X_1到X_2过程(或者说路径)都是历史空间的一个元素,用H(t_1,t_2)表示所有从时刻t_1到t_2的历史,这个空间有一个双纤维化结构(bi-fibration structure),记C(t_1)和C(t_2)表示两个时刻的状态空间(可以不一样)。
C(t_1)<---------H(t_1,t_2)---------->C(t_2)
向左这个箭头表示取 过程的起点,向右的箭头表示取过程的终点,这两个箭头都是纤维化。
上面这个图是数学中非常重要,非常常见的图,我们叫它 屋顶(roof),如果把中间的H画的高一点这个名字还是蛮恰当的。其实它有一个更专业的名字:span(参看nLab span 词条)。在这个图中如果把箭头都反过来,我们叫做cospan。这个图的重要性在于表达了两个集合之间二元关系的推广,几乎所有的对偶性和等价性的背后都有这么一个图像。比如傅里叶变换,朗兰兹对偶,森田等价等等。
如果把其中的一个箭头反过来,就是我们熟悉的可以复合两个函数的图像。但是span的箭头有一个方向不对,所以不能符合,但是span和span之间可以符合(做纤维积)。
在上面这个例子中,两个态之间的历史就刚好是这两个态的公共纤维,对这个纤维积分,得到的数就是两个态之间的关联振幅。所以历史求和或者路径积分的数学结构本质上是纤维积分。其实我们按照刚才自由向量空间的说法,我们可以把C(t_1)和C(t_2)中的元素作为指标比如用i,j 表示,历史空间中的公共纤维就可以用i,j标记,i和j的公共纤维记为P(i,j)(path or process)我们可以把这些纤维排成一个“矩阵”,对这个“矩阵”中的各个元素积分就得到一个真正的矩阵(我们还没有说这些纤维上有什么积分测度,我们后面再讲这些,先假设存在一个积分测度),我们记为S(t_1,t_2)这个矩阵就是传说中的S矩阵(S矩阵是量子物理的主要的也是最基本的观察量,S矩阵的系数叫做关联函数,共形场论中的S矩阵和黎曼面模空间上的conformal block,高斯-马宁联络也是有关的,这些S矩阵实际上构成一个Hopf algebra,这些都是后话)。所以量子化在态空间的层次上就是自由向量空间函子,在历史空间的层次上就是双纤维化+纤维积分。因为积分运算是线性算子所以这两个层次的操作是一致的。另外从上面的过程我们可以大致体验到categorical quantum field theory 就是S矩阵(Dyson-Schwinger formalism)的范畴化表述。
现在我们考虑三个相继时刻的情形。考虑三个相继时刻t_1,t_2,t_3, 对应的三个状态空间为C(t_1),C(t_2),C(t_3),其中的元素分别用i,j,k指标标记,这个时候我们有三个历史空间H(t_1),H(t_2),H(t_3),我们还有三个span(历史空间的双纤维化结构)
C(t_1)<------H(t_1,t_2)------->C(t_2),
C(t_2)<-------H(t_2,t_3)-------->C(t_3)
以及
C(t_1)<-------H(t_1,t_3)-------->C(t_3)
和前面的分析类似,由这三个span 我们可以得到三个散射矩阵S(t_1,t_2),S(t_2,t_3)和S(t_1,t_3)。
那么现在一个自然的问题就是所有的这些数据之间的关系是什么?
答案是H(t_1,t_2)和H(t_2,t_3)的关于C(t_2)纤维积(fiber producnt or pull back)刚好是H(t_1,t_3). 我们用span的语言来形式化这个结果就是前两个相继地span的复合是第三个span,这个不需要任何别的假设,只需要你承认我们的世界在时间的流逝下不会出现矛盾,就会自然的得到这个结果。学习这些东西其实不需要太多的数学和物理背景,真正本质的东西都是很简单很自然的。
我把上面的过程在解释一下,考虑t_1和t_3时刻的态i和k,他们之间的历史P(i,k)具有什么样的结构?如果我们在中间时刻t_2做一个观察,可以发现从i到k的过程可以根据在t_2时刻所经历的状态来划分,也就是说P(i,k)这个集合是所有的形如P(i,j)和P(j,k)的笛卡尔积 这样的集合的无交并(j取遍所有C(t_2)的元素)。现在我们开始做纤维积分,P(i,k)得到的积分是矩阵S(t_1,t_3)的i,k分量s_{ik},但是上面说到P(i,k)是一系列笛卡尔积的无交并,在笛卡尔积上做积分我们有富比尼定理(化重积分为累次积分),笛卡尔积P(i,j)P(j,k)的积分就是s_{ij}s_{jk},而在无交并空间上的积分就等于在各个子空间积分的和,
所以 我们得到s_{ik}=\sum_j s_{ij}s_{jk},这恰恰是矩阵乘积的公式,
所以S(t_1,t_3)=S(t_2,t_3)S(t_1,t_2).
在上面的证明中我忽略一些细节,就是历史空间上的测度问题。
其实要注意到量子场论的局部性对于上面的证明是非常要紧的,也就是说历史求和(路径积分)之所以有如此好的代数性质,关键的一条就是作用量的局部性。那么局部性到底什么意思呢?
局部性是指作用量对于过程的可加性(作用量对于时空是广延量)。也就是一个过程的作用量是它的各段中间过程的作用量的和。如果作用量是拉格朗日密度在时空上的积分的话,可加性自然成立。更精确一点,如果过程X=AB(A过程和B过程的复合),那么作用量S(X)=S(AB)=S(A)+S(B).
在做路径积分的时候,作用量是在指数上,所以exp^{S(X)}=exp^{S(A)}exp^{S(B)},
这一个性质保证了历史空间的乘积的测度等于历史空间测度的乘积。
强调一点: 作用量的可加性或者局部性是历史求和具有好的代数结构的先决条件。
一切都非常完美!
on shell-----------------我们上面介绍的东西其实都是在没有物理的一般情况的setting。这里物理指的就是作用量和历史空间上的测度。稍微懂点物理的都知道作用量是历史空间上的函数(通常叫做泛函,因为实际的例子中历史空间都是无限维的)。如果这个系统的物理不是很坏(nondegenerate),作用量实际上是一个莫尔斯函数。on shell 就是历史空间上作用量的极值点,它的物理意义就是经典的可以真实发生的过程(最小作用量原理)。微扰量子场论就是对on shell 进行形变量子化。如果假设作用量非退化,on shell 上会有一个自然的辛结构,这个辛结构是从作用量继承来的,基本上只要有非退化的变分结构,on shell 上都会有辛结构。如果退化我们只能得到预辛结构(pre-sympletic structure)。
通常遇到的例子,它们的状态空间都是同一个也就是和时间没有关系,而且由于on shell 是系统欧拉-拉格朗日方程的解空间,由于微分方程初值问题解的唯一性,所以可以把历史空间的on shell 部分和状态空间等同起来。
off shell-----------------历史空间上不在on shell上的点成为off shell, on shell 上的点都是可以真实发生的,或者满足物理约束的,比如它们满足能量守恒,动量守恒等等,但是off shell上的点不满足物理的限制,但是量子场论中要求off shell 的过程也会对真实的过程产生贡献(路径积分就是 对off shell的量子涨落进行累积),这些off shell 过程通常叫做虚过程,中间涉及的场的激发态叫做虚粒子。量子场论和凝聚态中对粒子的定义为场或者体系的具有一定稳定的特性的激发态,这些激发态通常是是场或者体系在某些相或者量子序下的低级激发态或者基态。
------------------------------------------------------------------------------
这一部分我们来回答以下一些问题。
拓扑量子场论中的拓扑到底意味着什么? 为什么要研究拓扑量子场论?拓扑量子场论又有现实的物理意义?
首先这些答案没有标准答案,数学家和物理学家的答案也不一样。
量子场论的主要的观察量就是散射矩阵或者叫S-matrix,当然如果是多个粒子到多个粒子的散射过程,这个矩阵实际上是一个高阶张量,当然高阶张量和张量空间之间的线性映射是一样。所以我们就不在精细的区分术语。散射矩阵的各个分量或者系数称为散射振幅或者转移振幅,通常物理学家把它们打包成生成函数,叫做所谓的关联函数。 除了一系列的散射矩阵之外,其他的一些主要要观测量就是一些算子的本征值本征态问题,即谱问题,还有系统的各种特殊态的对称性,能谱的研究。那么拓扑场论中的拓扑是什么意思呢?答案就是 拓扑的意思就是散射矩阵是拓扑不变量,或者说关联函数的系数或者散射矩阵的系数都是拓扑数。这是从数学的角度来说,从物理的角度就是,在拓扑场论中所有的粒子都是没有质量的,或者说有效质量为零。这一点和共形场论是一致的。拓扑场论和共形场论中的粒子都是没还有质量的,因为质量的定义是时空对称群的生成元的本征值,如果我们的理论和时空度规没有关系,那就是说是时空对称群的平凡表示,所以就不存在质量。更一般的判断拓扑性的方法(物理学家定义拓扑场论的方法)是看关联函数关于时空度规的变分是否为零,这一点比较接近S矩阵是拓扑不变量的解释。关联函数是拓扑的这个事情的物理图像是什么呢?
考虑时空上两个点或者多个点上发生了一些量子事件,或者说量子场在时空的一些点处出现一些激发或者退激,这些量子事件通常被说成是在这些点处插入顶点算子,这些顶点算子诱导了量子场的激发和退激,物理上要考虑这些量子事件的关联,也就是说这些事件背后有没有什么物理的或者动力学的原因,计算的结果就是关联函数。所以说关联函数是时空坐标的函数(顶点算子实际上是场位形坐标或者场动量坐标的量子化,物理学家通常看做是时空上的delta函数或者场的位形空间上的delta函数)。现在的问题,如果我连续的改变(当然要保证算子之间的时序结构不变)这些顶点算子在时空上插入的位置,关联函数会有什么变化? 答案是如果是拓扑场论的话,关联函数不会改变。那么为什么可以用对时空度规的变分为零来刻画关联函数的拓扑性呢? 这里涉及到主动和被动的描述的问题,改变顶点算子的位置可以等效的认为我改变了时空度规。或者说我可以通过一个微分同胚来实现顶点算子的位移,这个微分同胚可以诱导一个新的度规(比如可以通过pull back),顶点算子在原来的位置上的关联函数如果何在这个新的度规上的定点算子的关联函数是一样的话,那就必须对这个量子系统有一定的限制。这样的限制在共形场论中称为Ward恒等式。这个说法和改变顶点算子的位置而让关联函数不变是一样的。这个不变性不是必然要满足(不是逻辑必然的),如果要满足就说明这个系统是要受到约束的。
从上面的讨论我们也可以看出,相比较于经典场论,量子场论更像是一个黑箱子或者一台机器或者一块材料,为了了解量子场论的结构,我们给它一些刺激,看看它如何反映。这里的刺激就是我们在时空中插入一些顶点算子,来测量一些关联函数,通过这些关联函数我们来反推这个系统应该具有的结构。所以关联函数更像是控制系统的响应函数,知道了足够多的响应函数,我们基本上就了解了这个系统的行为模式。
说明这个事情一个比较好的例子就是黎曼流形上的hodge理论,有了黎曼度量之后我们可以定义调和形式,调和形式的空间和德拉姆上同调空间作为线性空间是同构的(不是作为弗洛比纽斯代数或者结合代数,调和形式上没有外积)。当我们改变黎曼度规的时候,调和形式空间会在微分形式空间转动和伸缩,但是调和形式空间的维数是不会变的,都等于Bitti numbers,说明他们是拓扑不变量。这个Hodge理论被威腾解释成一个超对称的量子力学,这个量子力学的波函数就是复值的微分形式全体(也可以考虑完备化的版本)
-------------------------------------------------------------------------------
1989年,M.Atiyha 受到Segal 公理化定义共形场论的方法的启发,给出了范畴化版本的拓扑量子场论的定义,指出了历史求和 与 流形的协边范畴的关联,揭示了量子场论的内在的数学结构。
拓扑量子场论的主要想法就是把时空解释成空间的定向协边。
时空=空间的定向协边
先解释一下什么是定向协边范畴。我们固定一个维数k,讨论k+1维定向协边范畴,k是空间维数,1表示时间维数。
这个范畴的对象是k维定向(闭)流形,比如M,我们+M和-M表示M的两个定向,它的物理意义就是量子场所生活的空间。两个定向相容的流形-M_1和+N_2(两个对象)之间的协边(协边范畴的态射)是一个k+1维定向流形L(定向反映的是时间方向),这个流形的定向要满足它在拓扑边界上诱导的定向是和M的定向相反和N的定向相同(统一用右手法则定义边界的诱导定向)。
我们可以把这个定向协边简单的写为
L=[-M]----->[+N],
中间的箭头表示时间的方向,L定义域-M表示的是过去的空间,+N表示未来的空间,因为时间是有确定方向的,所以在讨论两个k维闭流形之间的协边的时候 只需要给定L的定向那么定义域和值域的定向就自然确定了,也就是定义域的定向总是和诱导定向相反,值域的定向总是和诱导定向相同。
所有上面的协边可以更加简化为
L=M---->N 而不会引起歧义。
那么定向有什么物理意义呢?实际上,可以这样理解:
协边的定义域上生活的量子态对应于反粒子的激发态,协边的值域上生活的量子态对应于激发态,这是因为费曼把反粒子解释为沿反时间方向运动的粒子,把粒子解释为沿时间方向运动的粒子。这里正反的粒子的区分类似于 狄拉克的刀态(bra)和刃态(ket)的关系,说的更数学些就是 线性空间中的向量和其对偶空间 中的向量的关系。 当然更深刻的解释和CPT定理之类的物理有关,我们不必涉及这么复杂。
如果感觉协边的定向比较绕的话可以先不管这个东西。反正定向协边就是时空演化图,是量子场相互作用的舞台。和普通映射的复合一样,如果一个定向协边L_1的值域的定向和另一个定向协边L_2的值域有相同的定向,我们可以把L_1的值域和L_2的定义域等同起来而得到一个新的定向协边L,这个构造在拓扑上叫做空间的粘贴,在我们这里则把这个操作叫做定向协边的复合记做L=L_2L_1,这个复合和映射的复合满足相同的规律,即存在单位,满足结合律等等。其实这些规律是保证时空的因果结构所必须的。
阿提亚的伟大创见就在于发现时空的演化图(定向协边)和 量子物理中的 历史求和是相容的,换句话说 时空演化的代数结构(定向协边范畴)和量子场的转移振幅所满足的代数结构是一致的或者说 我们可以把定向协边看做是量子场的高维的 费曼图。 所以阿提亚把拓扑量子场论定义为定向协边范畴的线性表示。在粒子物理中,我们可以把量子场论定义为费曼图的表示,从费曼规则的意义上,阿提亚的拓扑量子场论是量子场论中费曼规则的高维推广或者说的更物理一些就是膜(相互作用)的费曼图。
一些简单的类比:
量子力学--------李群/李代数的表示
产生湮灭算子---------李代数的三角分解
(微扰)量子场论----------费曼图的表示
阿提亚的拓扑量子场论----------流形协边范畴的表示
总结一点: 阿提亚的拓扑量子场论是高维膜的量子场论。
下面我们讨论两类模型,来看看为什么历史求和会有如此好的代数结构。限于表达的限制,我只是提炼一些要点,详细的推导在推荐的材料里都有,很详细,很容易follow。
一类是规范模型,一类是sigma模型,这两类模型都可以看做是广义的上同调模型,区别于通常的广义上同调,拓扑量子场论是乘法的,而通常的广义上同调都是加法的。
大致上,在低能极限,对于「物质」(这里特指有质量粒子),只有「衰变」和「力」(流流相互作用)两种相互作用还有可观的强度,其中「力」还要求交换的粒子具有0质量,否则会有汤川势的屏蔽效应。
高能的多体相互作用太多了。甚至有一些非微扰的作用,比如瞬子instanton,多达12种粒子参与相互作用。
所以,忘了「力」吧,「相互作用」是一个广大的多的新世界! 发布于 2015-03-07
高能的多体相互作用太多了。甚至有一些非微扰的作用,比如瞬子instanton,多达12种粒子参与相互作用。
所以,忘了「力」吧,「相互作用」是一个广大的多的新世界! 发布于 2015-03-07
大致上,在低能极限,对于「物质」(这里特指有质量粒子),只有「衰变」和「力」(流流相互作用)两种相互作用还有可观的强度,其中「力」还要求交换的粒子具有0质量,否则会有汤川势的屏蔽效应。高能的多体相互作用太多了。甚至有一些非微扰的作用,比如… 显示全部

从微扰的观点看,一切相互作用都可以用散射刻画。而经典物理相当于散射能量远低于物质本身的能量,以至于物质的康普顿波长远小于物质间距。所谓高能,就是散射能量(相对速度)很大,两者可以靠近到非常短的距离内,使得康普顿波长覆盖彼此,量子效应放大,产生大量虚过程或交换大质量的中介粒子,允许的相互作用的形式变得非常多样
量子的随机性让问题变得更有趣:在运动方程的解附近可特出统计量。这也是量子场论大量使用路径积分或泛函积分的原因:用最小作用量原理得出经典/平均解,用线性微扰得出方差和关联。求出这些,还是用谐振子/常态分布的数学
学物理过程中,你有哪些问题是当时理解的比较肤浅,后来突然豁然开朗了?
如何给没学过量子场论的人科普量子场论这样的知识?
谢邀。
场论的科普工作上,我觉得徐一鸿做了相当不错的工作。参Anthony Zee, Quantum Field Theory in a Nutshell;Feynman也做得很好,参其着的《理性边缘的物理》(QED: The Strange Theory of Light and Matter)。
这是一个不容易的问题,因为场论其实没有什麽新的物理,它是一套系统的方法,把前人的东西简洁表示,然后以此为工具去研究新的问题。没有基本的物理知识(高中或本科程度),跟那人谈场论是没有意思的。不懂物理,场论只是一堆没有意义的数学。而且场论是一种很有趣的东西,读完好像懂,可以跟人谈笑风生,但用到上手却什麽都不会。
例子我主要用谐振子。其实,这个很实用,经典和量子都有解,而且大部分问题都由这个开始,理论家其实除了这个好像什麽也不懂⋯⋯
经典力学
我觉得要懂得量子场论,先要谈谈经典场论。谈经典场论前,先谈经典力学。
假设我们都懂得牛顿力学(不懂的话,场论对你来说没有意思⋯⋯),我们可以用牛顿第二定律得出其运动方程。后来有人发明了能量的概念,再后来有人发明了Lagrangian。需然这些都不是直接可量度的东西,但很有用,只要你写出 ,你可以用最小作用量原理(或Euler-Lagrange方程)得出一样的运动方程。
,你可以用最小作用量原理(或Euler-Lagrange方程)得出一样的运动方程。
这是一个系统:1. 识别系统的自由度;2. 写出系统的Lagrangian;3. 用最小作用量原理得出运动方程。你可能会问,既然我们有牛顿力学,为什麽要发明这个没有新物理意义的东西?答桉是:对于複杂点的系统,写出耦合的运动方程很难,但写出其Lagrangian相对容易,如两质点以一个弹簧连着,这两质点便有耦合,用我们的物理直觉,可自Lagrangian中有一耦合项为 ,再用系统的方法,便知运动方程。(当然这个简单问题,尚可用牛顿透程解决。)
,再用系统的方法,便知运动方程。(当然这个简单问题,尚可用牛顿透程解决。)
经典场论
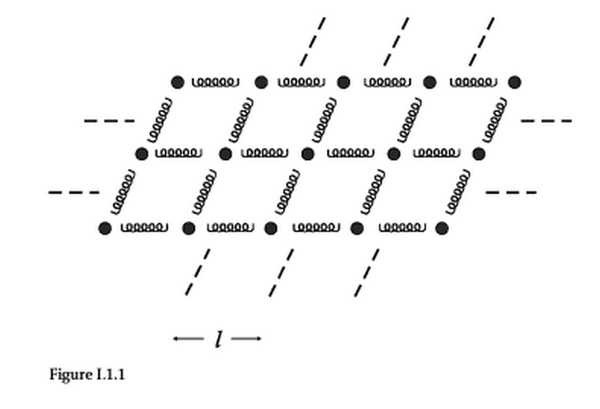
好了,讲完力学,可以讲场论了。上述的问题是单体或少体问题,场论一般处理多体问题。场是什麽?场(field)是空间(实空间、动量空间、或任何奇怪的空间)的函数(参如何让普通人理解物理学中「场」的本质? - 何史提的回答 )。用徐一鸿的方法说,场论处理的问题是一个床垫,找出一函数在床垫不同位置的便化。我们要用Lagrangian density,是场的泛函。同样地,用你的物理直觉,写出了Lagrangian density,再用最小作用量原理便可得运动方程。
经典场论的方程可以足够难解了。学到了这里,你可以跑去学机器学习了。
量子力学
经典力学中的一些量在量子力学便被量子化,有一些量不服从交换定律。这些东西大部分可在经典力学找到对应。可是,在经典力学视为可确定的,在量子力学变为随机,但随机量的平均值仍和经典力学一样。另外,在极限 ,量子力学回归经典力学,此即Correspondence Principle。
,量子力学回归经典力学,此即Correspondence Principle。
量子场论和统计场论
用Schrodinger方程的话,基本可解决很多单体或少体量子问题,但多体问题则需场论。跟经典力学一样,我们可写出其Lagrangian density,亦有系统的方法写出其运动方程,这运动方程跟经典力学的一样,但量子的随机性让问题变得更有趣:在运动方程的解附近可特出统计量。这也是量子场论大量使用路径积分或泛函积分的原因:用最小作用量原理得出经典/平均解,用线性微扰得出方差和关联。求出这些,还是用谐振子/常态分布的数学。
统计场论因其随机性,也有类似的东西,可用泛函积分,用最小自由能解得出平均场解,用linear response求出方差和关联(Kubo方程便和此有关)。古典和量的分别,只是一个用 ,另一用
,另一用 。
。
这好像很简单,但光是上两段,可能足以给一个博士学位,因为经典解也可能是极複杂的。还有,量子场论的微扰複杂得多。幸好我们有伟大的费曼图,简化了不少工作,而每一幅图都代表一项(包含积分式、格林函数/传播子),点的数量代表是微扰阶数。在相对论量子力学中,每一幅图都有物理意义,和某一事件发生的概率有关;在统计场论中,则纯綷代表数式。
微扰通常是小的量,但不幸地,这些费曼图中往往会给出发散的积分。那怎办?我们有重整化,在Lagrangian加些counter-term抵消发散项,而这些发散项可吸至Lagrangian。(参:微积分在微观量子世界还适用吗? - 何史提的回答)
在统计场论中,有一非微扰方法叫重整化群,是对系统作粗粒化处理(有点像在Chrome做zoom out一样),看看Lagrangian中每一项的变化是怎样,决定那些项留或不留。这个肯定和重整化有关,不过小弟还没通透。(参:重整群是不是一种粗粒化处理? - 何史提的回答)
另外,有孤立子的问题,如vortex和Skyrmions的;还有本人不熟悉的拓扑量子场论,什麽Chern-Simons项,很多好东西。
最后想强调这一点:场论本身没有为基本力学加点什麽物理,可是作为系统化的方法,让我们可以跑得跟远,研究更深刻的问题。如果没有物理基础就学场论,则是未学走路就先学跑。当用场论得到结果后,有洞见的物理学家绝对可以不用场论把物理图象清析地描述出来。这有点像基督教中的系统神学,一般信徒是不需要有系统神学训练的都可以过一个有爱心有喜乐的基督徒生命,但系统神学在一个有基础的基督徒可以助他走得更远,他也可深入浅出解析他领受的;但对于连圣经也未读懂的人,系统神学充其量是学术知识,对他能否有一个好的生命没有帮助
如何让普通人理解物理学中「场」的本质?
引力笔记- 弦乐四重奏- 博客大巴
场论的科普工作上,我觉得徐一鸿做了相当不错的工作。参Anthony Zee, Quantum Field Theory in a Nutshell;Feynman也做得很好,参其着的《理性边缘的物理》(QED: The Strange Theory of Light and Matter)。
这是一个不容易的问题,因为场论其实没有什麽新的物理,它是一套系统的方法,把前人的东西简洁表示,然后以此为工具去研究新的问题。没有基本的物理知识(高中或本科程度),跟那人谈场论是没有意思的。不懂物理,场论只是一堆没有意义的数学。而且场论是一种很有趣的东西,读完好像懂,可以跟人谈笑风生,但用到上手却什麽都不会。
例子我主要用谐振子。其实,这个很实用,经典和量子都有解,而且大部分问题都由这个开始,理论家其实除了这个好像什麽也不懂⋯⋯
经典力学
我觉得要懂得量子场论,先要谈谈经典场论。谈经典场论前,先谈经典力学。
假设我们都懂得牛顿力学(不懂的话,场论对你来说没有意思⋯⋯),我们可以用牛顿第二定律得出其运动方程。后来有人发明了能量的概念,再后来有人发明了Lagrangian。需然这些都不是直接可量度的东西,但很有用,只要你写出
这是一个系统:1. 识别系统的自由度;2. 写出系统的Lagrangian;3. 用最小作用量原理得出运动方程。你可能会问,既然我们有牛顿力学,为什麽要发明这个没有新物理意义的东西?答桉是:对于複杂点的系统,写出耦合的运动方程很难,但写出其Lagrangian相对容易,如两质点以一个弹簧连着,这两质点便有耦合,用我们的物理直觉,可自Lagrangian中有一耦合项为
经典场论

好了,讲完力学,可以讲场论了。上述的问题是单体或少体问题,场论一般处理多体问题。场是什麽?场(field)是空间(实空间、动量空间、或任何奇怪的空间)的函数(参如何让普通人理解物理学中「场」的本质? - 何史提的回答 )。用徐一鸿的方法说,场论处理的问题是一个床垫,找出一函数在床垫不同位置的便化。我们要用Lagrangian density,是场的泛函。同样地,用你的物理直觉,写出了Lagrangian density,再用最小作用量原理便可得运动方程。
经典场论的方程可以足够难解了。学到了这里,你可以跑去学机器学习了。
量子力学
经典力学中的一些量在量子力学便被量子化,有一些量不服从交换定律。这些东西大部分可在经典力学找到对应。可是,在经典力学视为可确定的,在量子力学变为随机,但随机量的平均值仍和经典力学一样。另外,在极限
量子场论和统计场论
用Schrodinger方程的话,基本可解决很多单体或少体量子问题,但多体问题则需场论。跟经典力学一样,我们可写出其Lagrangian density,亦有系统的方法写出其运动方程,这运动方程跟经典力学的一样,但量子的随机性让问题变得更有趣:在运动方程的解附近可特出统计量。这也是量子场论大量使用路径积分或泛函积分的原因:用最小作用量原理得出经典/平均解,用线性微扰得出方差和关联。求出这些,还是用谐振子/常态分布的数学。
统计场论因其随机性,也有类似的东西,可用泛函积分,用最小自由能解得出平均场解,用linear response求出方差和关联(Kubo方程便和此有关)。古典和量的分别,只是一个用
这好像很简单,但光是上两段,可能足以给一个博士学位,因为经典解也可能是极複杂的。还有,量子场论的微扰複杂得多。幸好我们有伟大的费曼图,简化了不少工作,而每一幅图都代表一项(包含积分式、格林函数/传播子),点的数量代表是微扰阶数。在相对论量子力学中,每一幅图都有物理意义,和某一事件发生的概率有关;在统计场论中,则纯綷代表数式。
微扰通常是小的量,但不幸地,这些费曼图中往往会给出发散的积分。那怎办?我们有重整化,在Lagrangian加些counter-term抵消发散项,而这些发散项可吸至Lagrangian。(参:微积分在微观量子世界还适用吗? - 何史提的回答)
在统计场论中,有一非微扰方法叫重整化群,是对系统作粗粒化处理(有点像在Chrome做zoom out一样),看看Lagrangian中每一项的变化是怎样,决定那些项留或不留。这个肯定和重整化有关,不过小弟还没通透。(参:重整群是不是一种粗粒化处理? - 何史提的回答)
另外,有孤立子的问题,如vortex和Skyrmions的;还有本人不熟悉的拓扑量子场论,什麽Chern-Simons项,很多好东西。
最后想强调这一点:场论本身没有为基本力学加点什麽物理,可是作为系统化的方法,让我们可以跑得跟远,研究更深刻的问题。如果没有物理基础就学场论,则是未学走路就先学跑。当用场论得到结果后,有洞见的物理学家绝对可以不用场论把物理图象清析地描述出来。这有点像基督教中的系统神学,一般信徒是不需要有系统神学训练的都可以过一个有爱心有喜乐的基督徒生命,但系统神学在一个有基础的基督徒可以助他走得更远,他也可深入浅出解析他领受的;但对于连圣经也未读懂的人,系统神学充其量是学术知识,对他能否有一个好的生命没有帮助
如何让普通人理解物理学中「场」的本质?
以前说到“引力场”,只知道大质量物体之间有引力相互作用,但是“场”是什么,完全没有概念。后来看一些科普的视频,又说引力场是一种时空塌陷(视频举的例子是在薄膜上放金属球,我知道这是给小白们看的形象化解释),然后我就更加糊涂了,场究竟是一种什么样的存在。
百度了一下“引力场”,发现是一个神棍似的解释(暗能量是什么东东?),不知道他们从哪里复制来的;维基百科上也只给了一个方程(好吧,看到方程,我没办法像魏成那样直接在大脑中产生图像)。
又百度了一下“磁场”,他们说磁场是一种物质。(!?)维基百科只解释了磁场是如何产生的。
那“场”究竟是什么?说是物质应该是不对的吧,如果是物质,它是由什么构成的?如果不是物质,但它又是真实存在的。
还有一点,好像经典力学里对引力场的解释和相对论对引力场解释差别很大,前者把引力场描述成磁力线那样的东西,而后者描述成时空塌陷(时空弯曲),所以我在想,“场”这个概念是不是因为现在人类科学还很落后,并没有搞清楚这一现象的本质,所以暂时借用一下“场”这个概念来描述和解释这个现象,但场并不是这些相互作用的本质?
我只是个小白,如果问了可笑的啥问题,请各位专业人士多多见谅。
======================================================================
请允许我修改一下我问题的关注点(不知道在知乎是否允许这样做?)
我尽量用我贫乏的语言描述清楚:
比如说,引力场。太阳与地球之间有引力,这种力是如何在两个物体间发生作用的?
现在的说法是因为有引力场作为媒介(?),现在还有假说存在“引力子”。
现在还发现,光辐射能产生“光压”,能使物体受到一定压力。那么是不是可以假设(请允许我胡说一下),太阳具有“光场”,所有受到太阳辐射的物体都能受到“光压力”。而这种力的产生,是由于光子的辐射。
那么引力的产生是否可以用同样的方式去理解,他是因为有质量的物体辐射“引力子”?
百度了一下“引力场”,发现是一个神棍似的解释(暗能量是什么东东?),不知道他们从哪里复制来的;维基百科上也只给了一个方程(好吧,看到方程,我没办法像魏成那样直接在大脑中产生图像)。
又百度了一下“磁场”,他们说磁场是一种物质。(!?)维基百科只解释了磁场是如何产生的。
那“场”究竟是什么?说是物质应该是不对的吧,如果是物质,它是由什么构成的?如果不是物质,但它又是真实存在的。
还有一点,好像经典力学里对引力场的解释和相对论对引力场解释差别很大,前者把引力场描述成磁力线那样的东西,而后者描述成时空塌陷(时空弯曲),所以我在想,“场”这个概念是不是因为现在人类科学还很落后,并没有搞清楚这一现象的本质,所以暂时借用一下“场”这个概念来描述和解释这个现象,但场并不是这些相互作用的本质?
我只是个小白,如果问了可笑的啥问题,请各位专业人士多多见谅。
======================================================================
请允许我修改一下我问题的关注点(不知道在知乎是否允许这样做?)
我尽量用我贫乏的语言描述清楚:
比如说,引力场。太阳与地球之间有引力,这种力是如何在两个物体间发生作用的?
现在的说法是因为有引力场作为媒介(?),现在还有假说存在“引力子”。
现在还发现,光辐射能产生“光压”,能使物体受到一定压力。那么是不是可以假设(请允许我胡说一下),太阳具有“光场”,所有受到太阳辐射的物体都能受到“光压力”。而这种力的产生,是由于光子的辐射。
那么引力的产生是否可以用同样的方式去理解,他是因为有质量的物体辐射“引力子”?
什么是答案总结? 答案总结
引力笔记- 弦乐四重奏- 博客大巴
但在实际操作中,我们选取正规化方案,时常也会受到物理的启发。姑举一例说明之。固体中的声子本来是晶体格子振动的模式,所以本来是非连续的有限自由度系统。用声子场描述之,是低能近似的结果。在接近及小于晶格间距的尺度上,用以描写声子的场论自然不合用了。所以,晶体本身为声子场理论提供了一个自然的正规化:将时空在晶格尺度上离散化为有限维系统,并宣布理论在此(能量)尺度以上失效。这里的晶格尺度,就是前文提到的正规化尺度Λ [5]。
由此不妨设想,时空本身也是离散的格子,只是这格子的间距极小,比当前对撞机所能达到的尺度还小得多,所以尚未被看到。如此一来,我们便可用晶格的方式做正规化,只要正规化的尺度Λ足够高,比高能实验中的典型能量尺度还高得多,则这种正规化方案似乎就合用,无论时空本身是否真的是晶格。
然而在粒子物理中,我们极少使用晶格正规化(除非做格点计算),而是它的各种修改版,因为晶格正规化显然破坏时空的连续对称性。但是,这些修改版中,截断尺度Λ的物理意义保留了下来(虽然在维数正规化(dimensional regularization)中这不甚明显)。所以,总的想法是,只要这截断尺度足够高就行了
奇异的量子信息远程传输
在图1中,我们展示了这样的data bus,它是由一些1/2自旋构成的梯子结构,每两个自旋点之间存在反铁磁Heisenberg相互作用,我们称之为自旋梯子。而A、B两点为两个外接自旋1/2的点,用以表示两个遥远的量子比特,它们同样以反铁磁Heisenberg相互作用与梯子相连。在图1(a)中,这两个量子比特B、A分别接在梯子的上、下两条腿上,并分别与R、L点相连。 在图1(b)中,这两个量子比特B、A都接在梯子的下两条腿上,并分别与R、L点相连。我们之所以要用自旋梯子作为data bus,是因为它的基态与激发态之间存在一个较大的能隙,也就是所谓的Haldane gap。由于能隙的保护,data bus保持了良好的相干性。
图2(a)展示了梯子部分的能谱结构。这可以从一个简单的角度来理解:当梯子两腿上的相互作用(图1中横向蓝色横线所代表)很弱而纵向相互作用(图1中横向蓝色竖线所代表)较强时,自旋梯子的基态是二聚化(dimerized)的(如图2(b)所示)。这时,它的低能激发是将一个单态转化为一个三重态。这时,当两腿上的横向相互作用变强时,横向相互作用将使得激发出来的三重态在梯子上跳越(如图2(b)所示),从而一个三重态的能级展宽为带结构(图2(a)中的蓝线)。当然,我们要问,当横向相互作用很强,以至于超过了纵向相互作用时,三重态的能级展宽的很厉害,会不会使得能隙消失呢。答案是不会,因为上述分析是在微扰的前提下进行的,即横向相互作用远小于纵向相互作用,当这个条件不成立时,我们需要更小心的处理这个强关联问题。事实上,Haldaane证明了无论横向或纵向相互作用是多少,自旋1/2的梯子模型总是具有一个能隙。
图3(a)展示了接入两个量子比特之后(图1(a)中的接法)的能谱。由于存在着较大的能隙保护,在环境温度较低小于能隙时,系统的性质由最下面的两个能级主导。这样,我们可以孤立出下面的两个能级,在它们形成的子空间内,写出由梯子诱导的A与B之间的有效耦合。它们的耦合强度由最低的两个能级差决定。这个相应的物理物理过程可以简单的表述如下:初始时,梯子处于基态,如果A自旋由于量子扰动翻转了一下,此时与之相连的L点(如图1所示)由于Heisenberg相互作用也会被翻转,这样就在梯子中产生了一个三重态激发,这个激发由于横向相互作用就在梯子中传播,当达到L点时L点的自旋翻转使得梯子中的三重态激发消失梯子回到原来的基态,同时B点的自旋被翻转。经过这样一个过程(图3(b)),梯子的状态未变,可是A点的翻转造成了B点的翻转,好像A直接与B耦合了一样——这种机制非常类似于超导里的电声子相互作用。
由此不妨设想,时空本身也是离散的格子,只是这格子的间距极小,比当前对撞机所能达到的尺度还小得多,所以尚未被看到。如此一来,我们便可用晶格的方式做正规化,只要正规化的尺度Λ足够高,比高能实验中的典型能量尺度还高得多,则这种正规化方案似乎就合用,无论时空本身是否真的是晶格。
然而在粒子物理中,我们极少使用晶格正规化(除非做格点计算),而是它的各种修改版,因为晶格正规化显然破坏时空的连续对称性。但是,这些修改版中,截断尺度Λ的物理意义保留了下来(虽然在维数正规化(dimensional regularization)中这不甚明显)。所以,总的想法是,只要这截断尺度足够高就行了
重整化辨义(一) - [且来悟理]
§1 引言
如果说相对论和量子论代表了现代物理学的两大理论基石,那么从这根基上成长出的最丰硕的成果,大概非量子场论莫属了。作为当代理论物理的标准范式之一,量子场论在好些方面都超出了早前的物理理论。首先是其应用的范围。从基本粒子物理,到凝聚态物理与生物物理,再到宇宙学,几乎穷尽了经验世界所有的尺度。其次是其精确性。作为量子场论典范理论的量子电动力学,是人类迄今所创造出的最精确的理论,其理论与实验十几位有效数字的吻合,为人津津乐道。
或许有人会说,量子场论之复杂艰难,也超过了任何早前的理论。而这倒未必。我觉得,这复杂和艰难很有可能只是由于场论的建立相对晚近,我们理解它的方式仍不够恰当、不够直接。也许物理学家需要经过更久的反刍,才能降低目前理解场论所需的势垒。不过可以聊以自慰的是,似乎任何全新的理论在初创时都是难懂的:我们都知道,Einstein在发明广义相对论后不久,有人对Eddington爵士说,世界上仅有2.5个人懂得它。可是,如果现在还有谁试图用这个故事来鼓吹相对论有多么难懂,我倒想和他分享另一个故事:《自然哲学的数学原理》成书时,有人评价道,Newton写了一本自己都看不懂的书。
不过话说回来,对多数初学者而言,量子场论的曲折繁复,是确凿无疑的。就我极有限的观察,在那些纷繁芜杂的概念中,没有什么比“重整化(renormalization)”引起了更多的误解。有意思的是,初学者的那些典型误解,正是老一辈学者的观点。最典型的例子是Dirac。他说:
“多数物理学家对此状况已非常满意。他们说:‘量子电动力学是个好理论,我们不必再为它苦恼了’。我必须说,我对这状况非常不满意,因为这个所谓的‘好理论’要忽略无穷大,要任意地忽略方程中的无穷大。这不是好的数学。好的数学是,你忽略一个量是因为它小——而不是因为它无穷大、而你又不想要它!”[1]
很明显,Dirac根本没有理解重整化的正确涵义。请注意,他说这话时已是1975年,彼时Wilson关于重整化群的文章业已发表。不过我们自然不可强求Dirac去理解重整化群,因为老一辈学者经常是无可救药的[2]。可是,如果今天还有谁要坚持Dirac的这种看法、还因为自己不正确的理解而攻击重整化本身,那又何异于成天反相对论的民科呢?
所以,我希望在此文中讨论重整化群理论的若干细节,以期有助于澄清某些常见的误解,包括刚才提到的Dirac式误解,也包括我自己在初学场论时时所持有的误解。如我的其它同类文章,在正文前,有必要作几点声明。
首先,我避免将本文做成教科书或讲义。所以,阅读本文不可代替阅读严肃的教科书,更不可代替亲自推导。事实上,若想对量子场论的任何概念有较扎实的理解,亲自推导是不二法门。我以为,单是数学推导的硬功夫有时就足以消除一些习见的误解。
同时,我也避免将本文做成科普,因为我希望澄清误解而不是创造误解。可是据我看,没有什么比科普创造了更多误解。所以,我会尽力将故事的逻辑解释清楚,但偶尔也会不加解释地使用一些并不初级的概念。我当然欢迎所有读者,但我设想读者至少有物理专业的背景。对于离理论物理较远的读者,我只能抱歉地说,读到哪里算哪里。如果遇到奇怪的符号或概念,就当作咒语吧。
为了清晰起见,我们只讨论量子场论的传统理论。此处所谓传统理论,在历史上是指物理学家从量子电动力学到重整化群理论的建立这段时间(1940s-1970s)所发展的场论,在技术上,则指相对论性的、具有经典极限的微扰量子场论。虽然更现代的非微扰方法提供了更有趣、并且也许是更重要的视角,但对本文而言,传统的微扰量子场论已经足够。
最后,我绝不敢妄称自己对这些理论有怎样完备的理解,所以错漏实在难免。不当之处,请读者指正。
§2 QFT in practice: 一切都是输入输出!
让我们以一个问题开始,即,作为一种物理(而不是数学或者形而上学)理论,量子场论如何工作。
大体上,和其他物理理论一样,量子场论可被视为输入输出系统。输入和输出端是可观测量,而其内核,则是一套数学公式体系。一种理论的物理意义就在于,将有限的可观测量输入理论后,理论可以通过公式体系的演绎,给出确定的、可供实验与观测检验的输出。至于这理论内核中的概念是否有经验世界的对应物,则不是物理理论所要解决的问题。
在量子场论的情形,输入输出端是关联函数。粒子探测器的计数、材料对激发的响应、宇宙的大尺度结构,这些可观测量在量子场论中都可化为关联函数。因此,将场论与实验观测建立联系,需要做两件事情:一是将观测量与关联函数建立联系,二是用理论计算关联函数。前者依赖于具体应用的场合且与本文关系不大,所以我们假设这一步已经做到,从而将关联函数径直视作可观测量。而后者,就是本文的中心问题。现在让我们讨论之。
至少在本文所关心的情形,关联函数总可被表达成路径积分,且这路径积分总能从配分函数通过泛函微商求得。因此,问题划归为计算配分函数。配分函数也是路径积分,它由两部分构成:被积泛函与积分测度。被积泛函是以经典作用量为相角的纯相位,而积分测度,一般来说是没有定义好的。我们或许可以像定义有限维线性空间的积分测度那样,将每个方向的微分形式简单地“乘”起来,但对于无穷多自由度来讲,这样做没有定义:正如简单地将所有自然数相加没有定义一样。因此需要其它更聪明的方式来定义这个测度。在场论中,为路径积分的测度赋予定义,就叫做正规化。
至于在实际应用中,我们极少直接定义此测度,因为我们通常并不计算配分函数,而是用微扰论,亦即Feynman图的方式,去逐阶计算散射矩阵元。这逐阶展开的参数,通常就是Planck常数h, 而展开的阶数,就是Feynman图的圈数。通常,领头阶,即“树图”,亦即h的零次项,并不依赖于泛函积分测度的定义,换用物理学家的术语,就是不依赖于正规化。所以,如果你只关心这一阶的结果,那的确不需要去为定义泛函积分的测度而费神[3]。但是,当我们计算圈图的时候,就会遇到麻烦:泛函积分测度无定义,在此就表现为圈积分的无穷大。这就是一切麻烦的根源。
于是,在圈图计算中,正规化的意思是,为圈积分找到合适的定义。这个问题很像为所有自然数的和找到一个定义。一旦被定义好,原来发散的圈积分就收敛于有限大的值了。
表面上看,这里所谓合适的定义,有相当大的自由度。因为,正规化只是将理论定义好的一种手段,不属于可直接观测的物理。但不难想见的是,正规化手续,即下定义的方式,会以某种方式与真实的物理相联系。事实上,当加入来自物理的限制(例如对称性)之后,合用的正规化方式往往相当有限。特别是当理论的对称性很强、从而其限制也很强时,合适的正规化时常求之不得。比如我们至今似乎还不知道如何正规化一个超对称的规范理论,使超对称与BRST对称性同时得以保持。
尽管如此,让我们暂时搁下这个问题,且假设已经找到了合适的正规化方法,并继续讨论量子场论如何工作。为确定起见,我们以量子电动力学(QED)为例。
§3 QED: 如何输入?如何输出?
QED的Lagrangian有两个未知参量(至少在表面看来如此[4]),即“电子质量项”的系数m0与电磁相互作用项的系数e0。所以我们需要至少两个输入量,才可以去计算更多可观测量。不要忘记,我们总是以关联函数为窗口做输入。所以,这里所谓的两个输入量,应该是出现在关联函数中的参量。若称这两个参量为A和B,则用 QED计算的结果应有如下形式:

从中反解出m0和e0,则Lagrangian中的未知参数就变为已知了。于是,我们可以用这个Lagrangian去计算更多关联函数,并和实验结果比对。
这就是QED工作的一般方式。当然,这是一个抽象且过分简化的叙述。现在,让我们在微扰论中逐阶解释之。
在第一阶(即树图),一切都很简单:我们选取电子的两点关联 ,以及双电子-光子的三点关联,作为输入量。除去并不重要的运动学与对称性结构,这两个关联函数就是电子的质量m与电磁作用的强度e。在树图阶,对这两个关联函数的计算结果,就是出现在Lagrangian中的参数m0和e0。于是,以上方程简化为,

的确,一切都很简单。但是请注意这个细节!我们并没有将m和e的测量结果直接赋给Lagrangian中的参数,而是赋给了关联函数。只是在树图近似下,这关联函数的理论结果恰好就是Lagrangian中的参数。无论如何,Lagrangian中的参数并不是可观测量。
现在让我们将以上操作做到下一阶(一圈图)。在操作上,一切都照旧:我们需要通过两点及三点关联函数输入m和e两个参量,然后用它们反推Lagrangian中的未知量m0和e0。
然而此时有两个新麻烦。一是,一圈图结果依赖于正规化,这一点前已述及。为确定起见,让我们将这结果对正规化的依赖记作对截断尺度Λ的依赖。另一个麻烦是,以上用作输入量的关联函数Γ,在一圈图中不仅仅依赖于参量m0与e0,还依赖于外动量p。考虑到这些复杂性,可知考虑进树图与一圈图之后,的计算结果应有如下形式:
![]() 这里不写等号,是因为m与m0,以及e与e0,都是不依赖于外动量的数。但是它们的差,即F与G,却依赖于外动量。所以以上表达式显然不够正确。正确的表达式,需要考虑如何测量m与e。如果它们是在低能实验中被测量的,则应取p=0。可这并非绝对的限制。假如实验是在某个相当高的尺度μ完成的,那更自然地选取应当是p=μ。即,
这里不写等号,是因为m与m0,以及e与e0,都是不依赖于外动量的数。但是它们的差,即F与G,却依赖于外动量。所以以上表达式显然不够正确。正确的表达式,需要考虑如何测量m与e。如果它们是在低能实验中被测量的,则应取p=0。可这并非绝对的限制。假如实验是在某个相当高的尺度μ完成的,那更自然地选取应当是p=μ。即,
![]() 这个尺度μ被称为重整化尺度,而这种从理论上定义可观测量的方式(即,将关联函数中冗余的外动量固定在一个尺度的方式),叫做一种重整化方案。需要注意的是,重整化尺度无论如何不是由实验完全决定的,而可以人为选取。反解以上方程,可得,
这个尺度μ被称为重整化尺度,而这种从理论上定义可观测量的方式(即,将关联函数中冗余的外动量固定在一个尺度的方式),叫做一种重整化方案。需要注意的是,重整化尺度无论如何不是由实验完全决定的,而可以人为选取。反解以上方程,可得,

这样,我们就获知了Lagrangian中的未知参数m0与e0,并可以用它们来计算其他可观测量,如电子的反常磁矩。
可是我们立刻会想到一个问题:经过这一套手续所得的Lagrangian的参数m0与e0,不仅依赖于实验输入m和e,还依赖于两个人为选取的参量μ和Λ——当然这本身不是问题,因为m0与e0属于理论的“内核”而非“接口”。我们的担心在于,用它们算出的可观测量是否也依赖于这两个人为选取的参量。当然,一个“好的”理论,其预言不应当强烈依赖于这些人为因素。
我们将在下一节解释,对于QED而言,重整化的奇妙之处,就在于用m0和e0算出的任何可观测量,对重整化尺度μ和截断尺度Λ的依赖都很弱。(当然,从重整化群理论的观点看来,这个“奇妙之处”完全在情理之中。)你会对这种很弱的依赖感到不适吗?如果会,请不要忘记,我们在使用微扰论做计算,所以在有限阶,本不应期待精确的结果。
§4 正规化方案?重整化方案?
我们在上一节看到,在一圈图水平,QED对可观测量的计算结果依赖于两个人为的参量:截断尺度Λ和重整化尺度μ。其实这只是整个故事的冰山一角。请回忆这两个人为的尺度是如何被引入的。截断尺度来自正规化方案,而重整化尺度来自重整化方案。所以,可观测量的一圈图结果,不只是依赖于两个人为的尺度,而且是两种人为的计算方案。为理解这种依赖性的意义,让我们稍稍进入细节。
先说正规化。前文已反复说明,正规化是定义路径积分测度的手续,在微扰论中,则表现为定义圈积分的手续。这种定义本身,原则上与经验世界并无直接对应,而纯粹是人工的产品。至于这样从心所欲的定义是否恰当,则要看由此导致的理论是否能通过实验观测的检验。实践中,最重要的检验来自对称性。我们在经验世界中观察到了很多很好的对称性,如相对论的时空对称性;我们在理论的构造中还可能因自洽性要求而不得不引入一些形似对称性的冗余自由度,如规范对称性。为了在量子场论中保持这些对称性,在定义正规化时自然要小心。对于时空对称性这种经验世界中的对称性,如果我们再做正规化时能保持它,自然很好;如果不能,亦非大碍,只要由此计算出的可观测量与实验结果吻合即可(这其实相当不容易!)。但是,对于规范对称性这类由理论自洽性要求的产物,正规化非保持它们不可。
但在实际操作中,我们选取正规化方案,时常也会受到物理的启发。姑举一例说明之。固体中的声子本来是晶体格子振动的模式,所以本来是非连续的有限自由度系统。用声子场描述之,是低能近似的结果。在接近及小于晶格间距的尺度上,用以描写声子的场论自然不合用了。所以,晶体本身为声子场理论提供了一个自然的正规化:将时空在晶格尺度上离散化为有限维系统,并宣布理论在此(能量)尺度以上失效。这里的晶格尺度,就是前文提到的正规化尺度Λ [5]。
由此不妨设想,时空本身也是离散的格子,只是这格子的间距极小,比当前对撞机所能达到的尺度还小得多,所以尚未被看到。如此一来,我们便可用晶格的方式做正规化,只要正规化的尺度Λ足够高,比高能实验中的典型能量尺度还高得多,则这种正规化方案似乎就合用,无论时空本身是否真的是晶格。
然而在粒子物理中,我们极少使用晶格正规化(除非做格点计算),而是它的各种修改版,因为晶格正规化显然破坏时空的连续对称性。但是,这些修改版中,截断尺度Λ的物理意义保留了下来(虽然在维数正规化(dimensional regularization)中这不甚明显)。所以,总的想法是,只要这截断尺度足够高就行了。
再说重整化方案。它比正规化方案简单地多。请回忆,在前一节中,我们用电子质量m与电磁作用强度e这两个观测量,在关联函数的外动量p等于一个特定的尺度μ时,为理论做初始输入。但这不是唯一的做法:只需注意到Lagrangian中有两个未知量,所以我们大可取任意两个“相互独立的”可观测量(比如各种四点关联函数),在任意的尺度μ做输入,然后将两个未知量反解出来即可。这种对输入量和输入尺度的选择,就叫做重整化方案。
明白了这些,我们就可以解释,用QED的一圈图所算出的可观测量,在多大程度上依赖于正规化方案和重整化方案。
仍然先讨论正规化。在上一节末,我们提到,用QED的圈图展开计算可观测量的结果,对截断尺度Λ的依赖很弱。现在我们来刻画这里的“很弱”有多弱。如果我们选择的正规化方案正确(比如,保持了所需的对称性),则由此计算出的可观测量对截断尺度Λ的依赖,总是形如 ,其中E是可观测量所在的典型能量尺度,而n是正整数。现在,既然Λ是一个任取的高(能量)尺度,则总可以将其取得任意高[6],从而可观测量对截断尺度的依赖就任意弱,所以总可以弱到实验测量的精度之内。因此,对正规化的依赖,不是问题。
,其中E是可观测量所在的典型能量尺度,而n是正整数。现在,既然Λ是一个任取的高(能量)尺度,则总可以将其取得任意高[6],从而可观测量对截断尺度的依赖就任意弱,所以总可以弱到实验测量的精度之内。因此,对正规化的依赖,不是问题。
请注意,我们单是陈述了这种依赖很弱,但并没有解释其原因。此处我们暂时不解释它,并将这视为一种“奇迹”。物理学家管QED的这种“奇迹”叫做“可重整性”,即是说,QED是一个“可重整化”的理论。反之,我们也有不可重整的理论,如广义相对论。如果说可重整性是奇迹,那么不可重整就是灾难。然而物理理论不是圣经,充满“奇迹”或“灾难”的故事自然无法令人满意。然而事实上,直到七十年代之后,物理学家借助重整化群理论,才理解了,为什么可重整的理论不是奇迹,而不可重整的理论不是灾难。这一点,我们将在以后解释。
现在我们讨论可观测量的理论计算结果对重整化方案的依赖性。按照前文,重整化方案包含两部分,一是选取作为输入的可观测量,二是选取输入的尺度μ。
关于输入量的选取,我们在QED中看到,选取电子的质量m和电磁作用的强度e,(至少在树图)可以简化表达式。然而在实践中,简化表达式的选取并非最佳,因为输入量自身携带着实验精度的限制。所以,最佳的方案,时常是选取那些实验上测量地最精确的量。事实上,这正是电弱理论的标准做法。所以,选取不同的输入量所引起的差别,一部分来自实验的误差,另一部分,来自微扰计算的误差,也就是忽略了更高圈图的误差。
至于输入尺度μ,一般而言,圈图结果对它的依赖时常形如 ,其中E是实验的典型能量。所以,在理想情形下,选取μ=E可使圈图结果为零,亦即,树图结果就足够精确了。然而,可观测量所对应的关联函数时常依赖于好几个能量E。所以在实际操作中,选取μ的方法往往是使得高圈图的修正尽量小。
,其中E是实验的典型能量。所以,在理想情形下,选取μ=E可使圈图结果为零,亦即,树图结果就足够精确了。然而,可观测量所对应的关联函数时常依赖于好几个能量E。所以在实际操作中,选取μ的方法往往是使得高圈图的修正尽量小。
所以,尽管对可观测量的计算结果依赖于人为地重整化方案,但这依赖是可控的:它们一方面来自实验误差,一方面来自微扰计算的误差。所以,如果假设实验误差为零,同时假设我们能算完微扰论的所有阶,那么结果应当完全不依赖于重整化方案。实践中,虽然这两假设都不成立,但此结论告诉我们,计算到微扰论的越高的阶数,使用不同重整化方案所造成的差别就越小。下面两张图来自QCD的实际计算[7],它们形象地展示了这个结论。
![]()
这两张图展示的计算结果是标准模型的Higgs粒子衰变到一对正反b夸克的衰变宽度(即衰变率的倒数),作为Higgs粒子质量的函数。两张图使用了两种不同的重整化方案。在每张图中,自上而下的曲线对应于微扰计算的阶数逐渐升高的结果。可以明显看到,随着计算到微扰论的更高阶,两种方案的结果越来越接近。同时,这两张图也清晰地展示了,随着阶数的升高,每一阶产生的修正在逐渐减小。这意味着,量子场论的微扰计算方法是可行的。
§5 正规化和重整化是严格的理论吗?
我希望上文已将量子场论工作的逻辑,以及正规化与重整化的初步想法讲清楚。在这过程中,我有意避免重复标准教科书的内容,而另取一种进路,介绍了量子场论,作为一种可以实际工作的理论,而不是板着脸吓唬人的理论,是如何运转的。请注意,自始至终,我们没有遇到“无穷大”的概念。所以Dirac式的质疑不攻自破。
与此同时,我想着意说明的是,我们面对的是一个精度有限的世界,所以并不在意绝对精确的结果,而允许有误差。只是,我希望通过上文已讲清楚,量子场论的微扰计算,尽管有误差,这误差却是可控的。的确,正是有了这套良好可控的计算手续,量子电动力学才有机会成为人类迄今为止所创造的最精确的物理理论。
如果有时间,我会在以后的文章中继续讨论更晚近的重整化群理论。但在此之前,我想谈谈,上文所描写的这套量子场论是否是严格的理论。之所以讨论这个问题,是因为我时常见到两种相反的意见。第一种意见说,量子场论中到处是无穷大,一片混乱。我们已经花了很大篇幅解释,为什么这种意见应该被扫进历史的垃圾堆。但另一种意见说,量子场论是可以被严格化的,同时,他们搬出处理路径积分的各种高深数学理论,并对那些认为重整化是耍流氓的同学说,读完这些艰深的数学,你就明白为什么路径积分是正确的了。
出于物理的角度而不是数学的角度,我个人对此问题的认识是这样。以本文描述的正规化的方式所建立起来的量子场论,可以被做成数学上严格的理论。——毕竟,如果用晶格正规化,我们所做的不过是有限维线性空间中的微积分。所以,这种严格化的方式甚至不需要借助任何高深的数学工具,也许大学一年级的数学知识就足够了。
但是有同学会问,如果换用另一种正规化呢?如果用动量截断正规化、或者维数正规化呢?——在这种情形下,这些正规化很可能只在微扰论的固定阶上有效,对于整个路径积分而言,它们很可能是没有被定义好的。但是,只要我们在做微扰计算,那就不是问题。这就是物理学家明知regularization by dimensional reduction(维数正规化的改进版)在高圈图是不自洽的,却仍然用它来处理超对称理论的原因。
但是,我得说,本文所描写的这套做法,极有可能不是量子场论在数学上的最终形式,即使它可以被严格化。事实上,我们这样处理量子场论的方法,很像Newton当年用几何学的无限分割处理微积分的方法。Newton用这套办法建立的力学是严格的理论吗?——如果我们承认实际测量的总是有限长的时间和有限长的距离,那么用Newton力学和实验比照时,就只需涉及有限量的比和有限量的求和,所以根本不需要导数和积分——你只要把那个区间做得足够小,就可以获得足够的精度。在这种意义上,由于只涉及四则运算,可以说这样的理论在数学上是严格的。换言之,我们用有限区间为Newton的那套涉及无穷量的运算提供了一种“正规化”。
我们当然知道,这不是最终的故事。实际的情形是,19世纪的数学家为Newton的微积分建立了严格的数学基础。至于物理学家,他们也从来不用有限区间的方式,亦即Newton在《原理》中所描写的那套繁琐的方式,去理解Newton力学,而是径直使用微积分。但是我想说,之所以如此,绝不是因为数学家已将微积分严格化,而是,使用微积分比处理有限区间的求和要简便得多。
所以,我的想法很清楚:也许数学家会在将来找到一种将量子场论以不借助于正规化的方式而严格化的方法,并且,这种方法比正规化的方式要简便地多容易地多。但是在此之前,对于物理学家来讲,如果单是为了理解重整化理论,那些高深的数学就纯属多余。
-------------------------------
[1] 本文作者译自renormalization的Wikipedia词条,转引自Kragh, Helge ; Dirac: A scientific biography, CUP 1990, p. 184。
[2] Max Planck说:“新生的科学真理并非通过说服它的反对者而取得胜利,而是,它的反对者最终死去、熟悉这真理的新一代成长起来。”
[3] 至于为何树图结果不依赖于泛函积分测度的定义,有一种直观的理解。如所周知,在通常的配分函数中,被积泛函是经典作用量的指数,它包含经典理论的所有信息。而路径积分的测度,则包含相应的量子理论的信息。正文中又提到,树图结果通常不依赖于Planck常数,所以基本上是经典理论的结果,所以自然不会依赖于路径积分的测度。
[4] 更仔细的讨论,须考虑电子场与光子场的归一化。但由于QED的规范对称性,它们并不是独立的量。所以为清晰起见,我们在下文中亦不考虑这两种归一化的量子修正。
[5] 我们使用自然单位制,所以混用空间尺度和能量尺度。
[6] 我请内行的读者在此暂时忘记QED的Landau极点。
[7] A. L. Kataev and V. T. Kim, arXiv: 0902.1442。
如果说相对论和量子论代表了现代物理学的两大理论基石,那么从这根基上成长出的最丰硕的成果,大概非量子场论莫属了。作为当代理论物理的标准范式之一,量子场论在好些方面都超出了早前的物理理论。首先是其应用的范围。从基本粒子物理,到凝聚态物理与生物物理,再到宇宙学,几乎穷尽了经验世界所有的尺度。其次是其精确性。作为量子场论典范理论的量子电动力学,是人类迄今所创造出的最精确的理论,其理论与实验十几位有效数字的吻合,为人津津乐道。
或许有人会说,量子场论之复杂艰难,也超过了任何早前的理论。而这倒未必。我觉得,这复杂和艰难很有可能只是由于场论的建立相对晚近,我们理解它的方式仍不够恰当、不够直接。也许物理学家需要经过更久的反刍,才能降低目前理解场论所需的势垒。不过可以聊以自慰的是,似乎任何全新的理论在初创时都是难懂的:我们都知道,Einstein在发明广义相对论后不久,有人对Eddington爵士说,世界上仅有2.5个人懂得它。可是,如果现在还有谁试图用这个故事来鼓吹相对论有多么难懂,我倒想和他分享另一个故事:《自然哲学的数学原理》成书时,有人评价道,Newton写了一本自己都看不懂的书。
不过话说回来,对多数初学者而言,量子场论的曲折繁复,是确凿无疑的。就我极有限的观察,在那些纷繁芜杂的概念中,没有什么比“重整化(renormalization)”引起了更多的误解。有意思的是,初学者的那些典型误解,正是老一辈学者的观点。最典型的例子是Dirac。他说:
“多数物理学家对此状况已非常满意。他们说:‘量子电动力学是个好理论,我们不必再为它苦恼了’。我必须说,我对这状况非常不满意,因为这个所谓的‘好理论’要忽略无穷大,要任意地忽略方程中的无穷大。这不是好的数学。好的数学是,你忽略一个量是因为它小——而不是因为它无穷大、而你又不想要它!”[1]
很明显,Dirac根本没有理解重整化的正确涵义。请注意,他说这话时已是1975年,彼时Wilson关于重整化群的文章业已发表。不过我们自然不可强求Dirac去理解重整化群,因为老一辈学者经常是无可救药的[2]。可是,如果今天还有谁要坚持Dirac的这种看法、还因为自己不正确的理解而攻击重整化本身,那又何异于成天反相对论的民科呢?
所以,我希望在此文中讨论重整化群理论的若干细节,以期有助于澄清某些常见的误解,包括刚才提到的Dirac式误解,也包括我自己在初学场论时时所持有的误解。如我的其它同类文章,在正文前,有必要作几点声明。
首先,我避免将本文做成教科书或讲义。所以,阅读本文不可代替阅读严肃的教科书,更不可代替亲自推导。事实上,若想对量子场论的任何概念有较扎实的理解,亲自推导是不二法门。我以为,单是数学推导的硬功夫有时就足以消除一些习见的误解。
同时,我也避免将本文做成科普,因为我希望澄清误解而不是创造误解。可是据我看,没有什么比科普创造了更多误解。所以,我会尽力将故事的逻辑解释清楚,但偶尔也会不加解释地使用一些并不初级的概念。我当然欢迎所有读者,但我设想读者至少有物理专业的背景。对于离理论物理较远的读者,我只能抱歉地说,读到哪里算哪里。如果遇到奇怪的符号或概念,就当作咒语吧。
为了清晰起见,我们只讨论量子场论的传统理论。此处所谓传统理论,在历史上是指物理学家从量子电动力学到重整化群理论的建立这段时间(1940s-1970s)所发展的场论,在技术上,则指相对论性的、具有经典极限的微扰量子场论。虽然更现代的非微扰方法提供了更有趣、并且也许是更重要的视角,但对本文而言,传统的微扰量子场论已经足够。
最后,我绝不敢妄称自己对这些理论有怎样完备的理解,所以错漏实在难免。不当之处,请读者指正。
§2 QFT in practice: 一切都是输入输出!
让我们以一个问题开始,即,作为一种物理(而不是数学或者形而上学)理论,量子场论如何工作。
大体上,和其他物理理论一样,量子场论可被视为输入输出系统。输入和输出端是可观测量,而其内核,则是一套数学公式体系。一种理论的物理意义就在于,将有限的可观测量输入理论后,理论可以通过公式体系的演绎,给出确定的、可供实验与观测检验的输出。至于这理论内核中的概念是否有经验世界的对应物,则不是物理理论所要解决的问题。
在量子场论的情形,输入输出端是关联函数。粒子探测器的计数、材料对激发的响应、宇宙的大尺度结构,这些可观测量在量子场论中都可化为关联函数。因此,将场论与实验观测建立联系,需要做两件事情:一是将观测量与关联函数建立联系,二是用理论计算关联函数。前者依赖于具体应用的场合且与本文关系不大,所以我们假设这一步已经做到,从而将关联函数径直视作可观测量。而后者,就是本文的中心问题。现在让我们讨论之。
至少在本文所关心的情形,关联函数总可被表达成路径积分,且这路径积分总能从配分函数通过泛函微商求得。因此,问题划归为计算配分函数。配分函数也是路径积分,它由两部分构成:被积泛函与积分测度。被积泛函是以经典作用量为相角的纯相位,而积分测度,一般来说是没有定义好的。我们或许可以像定义有限维线性空间的积分测度那样,将每个方向的微分形式简单地“乘”起来,但对于无穷多自由度来讲,这样做没有定义:正如简单地将所有自然数相加没有定义一样。因此需要其它更聪明的方式来定义这个测度。在场论中,为路径积分的测度赋予定义,就叫做正规化。
至于在实际应用中,我们极少直接定义此测度,因为我们通常并不计算配分函数,而是用微扰论,亦即Feynman图的方式,去逐阶计算散射矩阵元。这逐阶展开的参数,通常就是Planck常数h, 而展开的阶数,就是Feynman图的圈数。通常,领头阶,即“树图”,亦即h的零次项,并不依赖于泛函积分测度的定义,换用物理学家的术语,就是不依赖于正规化。所以,如果你只关心这一阶的结果,那的确不需要去为定义泛函积分的测度而费神[3]。但是,当我们计算圈图的时候,就会遇到麻烦:泛函积分测度无定义,在此就表现为圈积分的无穷大。这就是一切麻烦的根源。
于是,在圈图计算中,正规化的意思是,为圈积分找到合适的定义。这个问题很像为所有自然数的和找到一个定义。一旦被定义好,原来发散的圈积分就收敛于有限大的值了。
表面上看,这里所谓合适的定义,有相当大的自由度。因为,正规化只是将理论定义好的一种手段,不属于可直接观测的物理。但不难想见的是,正规化手续,即下定义的方式,会以某种方式与真实的物理相联系。事实上,当加入来自物理的限制(例如对称性)之后,合用的正规化方式往往相当有限。特别是当理论的对称性很强、从而其限制也很强时,合适的正规化时常求之不得。比如我们至今似乎还不知道如何正规化一个超对称的规范理论,使超对称与BRST对称性同时得以保持。
尽管如此,让我们暂时搁下这个问题,且假设已经找到了合适的正规化方法,并继续讨论量子场论如何工作。为确定起见,我们以量子电动力学(QED)为例。
§3 QED: 如何输入?如何输出?
QED的Lagrangian有两个未知参量(至少在表面看来如此[4]),即“电子质量项”的系数m0与电磁相互作用项的系数e0。所以我们需要至少两个输入量,才可以去计算更多可观测量。不要忘记,我们总是以关联函数为窗口做输入。所以,这里所谓的两个输入量,应该是出现在关联函数中的参量。若称这两个参量为A和B,则用 QED计算的结果应有如下形式:

从中反解出m0和e0,则Lagrangian中的未知参数就变为已知了。于是,我们可以用这个Lagrangian去计算更多关联函数,并和实验结果比对。
这就是QED工作的一般方式。当然,这是一个抽象且过分简化的叙述。现在,让我们在微扰论中逐阶解释之。
在第一阶(即树图),一切都很简单:我们选取电子的两点关联 ,以及双电子-光子的三点关联,作为输入量。除去并不重要的运动学与对称性结构,这两个关联函数就是电子的质量m与电磁作用的强度e。在树图阶,对这两个关联函数的计算结果,就是出现在Lagrangian中的参数m0和e0。于是,以上方程简化为,

的确,一切都很简单。但是请注意这个细节!我们并没有将m和e的测量结果直接赋给Lagrangian中的参数,而是赋给了关联函数。只是在树图近似下,这关联函数的理论结果恰好就是Lagrangian中的参数。无论如何,Lagrangian中的参数并不是可观测量。
现在让我们将以上操作做到下一阶(一圈图)。在操作上,一切都照旧:我们需要通过两点及三点关联函数输入m和e两个参量,然后用它们反推Lagrangian中的未知量m0和e0。
然而此时有两个新麻烦。一是,一圈图结果依赖于正规化,这一点前已述及。为确定起见,让我们将这结果对正规化的依赖记作对截断尺度Λ的依赖。另一个麻烦是,以上用作输入量的关联函数Γ,在一圈图中不仅仅依赖于参量m0与e0,还依赖于外动量p。考虑到这些复杂性,可知考虑进树图与一圈图之后,的计算结果应有如下形式:

这样,我们就获知了Lagrangian中的未知参数m0与e0,并可以用它们来计算其他可观测量,如电子的反常磁矩。
可是我们立刻会想到一个问题:经过这一套手续所得的Lagrangian的参数m0与e0,不仅依赖于实验输入m和e,还依赖于两个人为选取的参量μ和Λ——当然这本身不是问题,因为m0与e0属于理论的“内核”而非“接口”。我们的担心在于,用它们算出的可观测量是否也依赖于这两个人为选取的参量。当然,一个“好的”理论,其预言不应当强烈依赖于这些人为因素。
我们将在下一节解释,对于QED而言,重整化的奇妙之处,就在于用m0和e0算出的任何可观测量,对重整化尺度μ和截断尺度Λ的依赖都很弱。(当然,从重整化群理论的观点看来,这个“奇妙之处”完全在情理之中。)你会对这种很弱的依赖感到不适吗?如果会,请不要忘记,我们在使用微扰论做计算,所以在有限阶,本不应期待精确的结果。
§4 正规化方案?重整化方案?
我们在上一节看到,在一圈图水平,QED对可观测量的计算结果依赖于两个人为的参量:截断尺度Λ和重整化尺度μ。其实这只是整个故事的冰山一角。请回忆这两个人为的尺度是如何被引入的。截断尺度来自正规化方案,而重整化尺度来自重整化方案。所以,可观测量的一圈图结果,不只是依赖于两个人为的尺度,而且是两种人为的计算方案。为理解这种依赖性的意义,让我们稍稍进入细节。
先说正规化。前文已反复说明,正规化是定义路径积分测度的手续,在微扰论中,则表现为定义圈积分的手续。这种定义本身,原则上与经验世界并无直接对应,而纯粹是人工的产品。至于这样从心所欲的定义是否恰当,则要看由此导致的理论是否能通过实验观测的检验。实践中,最重要的检验来自对称性。我们在经验世界中观察到了很多很好的对称性,如相对论的时空对称性;我们在理论的构造中还可能因自洽性要求而不得不引入一些形似对称性的冗余自由度,如规范对称性。为了在量子场论中保持这些对称性,在定义正规化时自然要小心。对于时空对称性这种经验世界中的对称性,如果我们再做正规化时能保持它,自然很好;如果不能,亦非大碍,只要由此计算出的可观测量与实验结果吻合即可(这其实相当不容易!)。但是,对于规范对称性这类由理论自洽性要求的产物,正规化非保持它们不可。
但在实际操作中,我们选取正规化方案,时常也会受到物理的启发。姑举一例说明之。固体中的声子本来是晶体格子振动的模式,所以本来是非连续的有限自由度系统。用声子场描述之,是低能近似的结果。在接近及小于晶格间距的尺度上,用以描写声子的场论自然不合用了。所以,晶体本身为声子场理论提供了一个自然的正规化:将时空在晶格尺度上离散化为有限维系统,并宣布理论在此(能量)尺度以上失效。这里的晶格尺度,就是前文提到的正规化尺度Λ [5]。
由此不妨设想,时空本身也是离散的格子,只是这格子的间距极小,比当前对撞机所能达到的尺度还小得多,所以尚未被看到。如此一来,我们便可用晶格的方式做正规化,只要正规化的尺度Λ足够高,比高能实验中的典型能量尺度还高得多,则这种正规化方案似乎就合用,无论时空本身是否真的是晶格。
然而在粒子物理中,我们极少使用晶格正规化(除非做格点计算),而是它的各种修改版,因为晶格正规化显然破坏时空的连续对称性。但是,这些修改版中,截断尺度Λ的物理意义保留了下来(虽然在维数正规化(dimensional regularization)中这不甚明显)。所以,总的想法是,只要这截断尺度足够高就行了。
再说重整化方案。它比正规化方案简单地多。请回忆,在前一节中,我们用电子质量m与电磁作用强度e这两个观测量,在关联函数的外动量p等于一个特定的尺度μ时,为理论做初始输入。但这不是唯一的做法:只需注意到Lagrangian中有两个未知量,所以我们大可取任意两个“相互独立的”可观测量(比如各种四点关联函数),在任意的尺度μ做输入,然后将两个未知量反解出来即可。这种对输入量和输入尺度的选择,就叫做重整化方案。
明白了这些,我们就可以解释,用QED的一圈图所算出的可观测量,在多大程度上依赖于正规化方案和重整化方案。
仍然先讨论正规化。在上一节末,我们提到,用QED的圈图展开计算可观测量的结果,对截断尺度Λ的依赖很弱。现在我们来刻画这里的“很弱”有多弱。如果我们选择的正规化方案正确(比如,保持了所需的对称性),则由此计算出的可观测量对截断尺度Λ的依赖,总是形如
 ,其中E是可观测量所在的典型能量尺度,而n是正整数。现在,既然Λ是一个任取的高(能量)尺度,则总可以将其取得任意高[6],从而可观测量对截断尺度的依赖就任意弱,所以总可以弱到实验测量的精度之内。因此,对正规化的依赖,不是问题。
,其中E是可观测量所在的典型能量尺度,而n是正整数。现在,既然Λ是一个任取的高(能量)尺度,则总可以将其取得任意高[6],从而可观测量对截断尺度的依赖就任意弱,所以总可以弱到实验测量的精度之内。因此,对正规化的依赖,不是问题。请注意,我们单是陈述了这种依赖很弱,但并没有解释其原因。此处我们暂时不解释它,并将这视为一种“奇迹”。物理学家管QED的这种“奇迹”叫做“可重整性”,即是说,QED是一个“可重整化”的理论。反之,我们也有不可重整的理论,如广义相对论。如果说可重整性是奇迹,那么不可重整就是灾难。然而物理理论不是圣经,充满“奇迹”或“灾难”的故事自然无法令人满意。然而事实上,直到七十年代之后,物理学家借助重整化群理论,才理解了,为什么可重整的理论不是奇迹,而不可重整的理论不是灾难。这一点,我们将在以后解释。
现在我们讨论可观测量的理论计算结果对重整化方案的依赖性。按照前文,重整化方案包含两部分,一是选取作为输入的可观测量,二是选取输入的尺度μ。
关于输入量的选取,我们在QED中看到,选取电子的质量m和电磁作用的强度e,(至少在树图)可以简化表达式。然而在实践中,简化表达式的选取并非最佳,因为输入量自身携带着实验精度的限制。所以,最佳的方案,时常是选取那些实验上测量地最精确的量。事实上,这正是电弱理论的标准做法。所以,选取不同的输入量所引起的差别,一部分来自实验的误差,另一部分,来自微扰计算的误差,也就是忽略了更高圈图的误差。
至于输入尺度μ,一般而言,圈图结果对它的依赖时常形如
 ,其中E是实验的典型能量。所以,在理想情形下,选取μ=E可使圈图结果为零,亦即,树图结果就足够精确了。然而,可观测量所对应的关联函数时常依赖于好几个能量E。所以在实际操作中,选取μ的方法往往是使得高圈图的修正尽量小。
,其中E是实验的典型能量。所以,在理想情形下,选取μ=E可使圈图结果为零,亦即,树图结果就足够精确了。然而,可观测量所对应的关联函数时常依赖于好几个能量E。所以在实际操作中,选取μ的方法往往是使得高圈图的修正尽量小。所以,尽管对可观测量的计算结果依赖于人为地重整化方案,但这依赖是可控的:它们一方面来自实验误差,一方面来自微扰计算的误差。所以,如果假设实验误差为零,同时假设我们能算完微扰论的所有阶,那么结果应当完全不依赖于重整化方案。实践中,虽然这两假设都不成立,但此结论告诉我们,计算到微扰论的越高的阶数,使用不同重整化方案所造成的差别就越小。下面两张图来自QCD的实际计算[7],它们形象地展示了这个结论。
这两张图展示的计算结果是标准模型的Higgs粒子衰变到一对正反b夸克的衰变宽度(即衰变率的倒数),作为Higgs粒子质量的函数。两张图使用了两种不同的重整化方案。在每张图中,自上而下的曲线对应于微扰计算的阶数逐渐升高的结果。可以明显看到,随着计算到微扰论的更高阶,两种方案的结果越来越接近。同时,这两张图也清晰地展示了,随着阶数的升高,每一阶产生的修正在逐渐减小。这意味着,量子场论的微扰计算方法是可行的。
§5 正规化和重整化是严格的理论吗?
我希望上文已将量子场论工作的逻辑,以及正规化与重整化的初步想法讲清楚。在这过程中,我有意避免重复标准教科书的内容,而另取一种进路,介绍了量子场论,作为一种可以实际工作的理论,而不是板着脸吓唬人的理论,是如何运转的。请注意,自始至终,我们没有遇到“无穷大”的概念。所以Dirac式的质疑不攻自破。
与此同时,我想着意说明的是,我们面对的是一个精度有限的世界,所以并不在意绝对精确的结果,而允许有误差。只是,我希望通过上文已讲清楚,量子场论的微扰计算,尽管有误差,这误差却是可控的。的确,正是有了这套良好可控的计算手续,量子电动力学才有机会成为人类迄今为止所创造的最精确的物理理论。
如果有时间,我会在以后的文章中继续讨论更晚近的重整化群理论。但在此之前,我想谈谈,上文所描写的这套量子场论是否是严格的理论。之所以讨论这个问题,是因为我时常见到两种相反的意见。第一种意见说,量子场论中到处是无穷大,一片混乱。我们已经花了很大篇幅解释,为什么这种意见应该被扫进历史的垃圾堆。但另一种意见说,量子场论是可以被严格化的,同时,他们搬出处理路径积分的各种高深数学理论,并对那些认为重整化是耍流氓的同学说,读完这些艰深的数学,你就明白为什么路径积分是正确的了。
出于物理的角度而不是数学的角度,我个人对此问题的认识是这样。以本文描述的正规化的方式所建立起来的量子场论,可以被做成数学上严格的理论。——毕竟,如果用晶格正规化,我们所做的不过是有限维线性空间中的微积分。所以,这种严格化的方式甚至不需要借助任何高深的数学工具,也许大学一年级的数学知识就足够了。
但是有同学会问,如果换用另一种正规化呢?如果用动量截断正规化、或者维数正规化呢?——在这种情形下,这些正规化很可能只在微扰论的固定阶上有效,对于整个路径积分而言,它们很可能是没有被定义好的。但是,只要我们在做微扰计算,那就不是问题。这就是物理学家明知regularization by dimensional reduction(维数正规化的改进版)在高圈图是不自洽的,却仍然用它来处理超对称理论的原因。
但是,我得说,本文所描写的这套做法,极有可能不是量子场论在数学上的最终形式,即使它可以被严格化。事实上,我们这样处理量子场论的方法,很像Newton当年用几何学的无限分割处理微积分的方法。Newton用这套办法建立的力学是严格的理论吗?——如果我们承认实际测量的总是有限长的时间和有限长的距离,那么用Newton力学和实验比照时,就只需涉及有限量的比和有限量的求和,所以根本不需要导数和积分——你只要把那个区间做得足够小,就可以获得足够的精度。在这种意义上,由于只涉及四则运算,可以说这样的理论在数学上是严格的。换言之,我们用有限区间为Newton的那套涉及无穷量的运算提供了一种“正规化”。
我们当然知道,这不是最终的故事。实际的情形是,19世纪的数学家为Newton的微积分建立了严格的数学基础。至于物理学家,他们也从来不用有限区间的方式,亦即Newton在《原理》中所描写的那套繁琐的方式,去理解Newton力学,而是径直使用微积分。但是我想说,之所以如此,绝不是因为数学家已将微积分严格化,而是,使用微积分比处理有限区间的求和要简便得多。
所以,我的想法很清楚:也许数学家会在将来找到一种将量子场论以不借助于正规化的方式而严格化的方法,并且,这种方法比正规化的方式要简便地多容易地多。但是在此之前,对于物理学家来讲,如果单是为了理解重整化理论,那些高深的数学就纯属多余。
-------------------------------
[1] 本文作者译自renormalization的Wikipedia词条,转引自Kragh, Helge ; Dirac: A scientific biography, CUP 1990, p. 184。
[2] Max Planck说:“新生的科学真理并非通过说服它的反对者而取得胜利,而是,它的反对者最终死去、熟悉这真理的新一代成长起来。”
[3] 至于为何树图结果不依赖于泛函积分测度的定义,有一种直观的理解。如所周知,在通常的配分函数中,被积泛函是经典作用量的指数,它包含经典理论的所有信息。而路径积分的测度,则包含相应的量子理论的信息。正文中又提到,树图结果通常不依赖于Planck常数,所以基本上是经典理论的结果,所以自然不会依赖于路径积分的测度。
[4] 更仔细的讨论,须考虑电子场与光子场的归一化。但由于QED的规范对称性,它们并不是独立的量。所以为清晰起见,我们在下文中亦不考虑这两种归一化的量子修正。
[5] 我们使用自然单位制,所以混用空间尺度和能量尺度。
[6] 我请内行的读者在此暂时忘记QED的Landau极点。
[7] A. L. Kataev and V. T. Kim, arXiv: 0902.1442。
奇异的量子信息远程传输
石弢
量子计算机的提出已经有三十多年的历史了,人们在一直不断的努力寻找可以实现量子计算机的器件。九十年代出,随着激光制冷等技术的发展,人们可以冷却原子,进而发现冷原子系综可以成为实现量子计算的良好候选者。但是由于原子质心平动造成的较强的量子退相干,它并不能实现理想的量子计算。后来,人们又找到了一种可以实现近理想量子计算的器件,即所谓的约瑟夫森结或超导量子干涉仪(SQUID)。由于它具有较长的量子退相干时间,所以它可以实现比较理想的量子操作和量子计算。直到现在,关于SQUID理论和应用的研究还在如火如荼的进行着。2007年左右,人们又提出了基于量子霍耳液体和自旋液体的拓扑量子计算。由于体系的拓扑稳定性,它的状态极不容易受到局域微扰的影响。除非改变系统的拓扑结构——整体几何结构——才有可能改变体系的状态。而环境的影响一般不会改变体系的拓扑,所以像量子霍耳液体这种凝聚态体系利用其具有的拓扑序极好的保护了它的相干性,具有较长的退相干时间。但是,这种具有拓扑序的系统在实际中是很难操作的。无论如何,理想的量子计算需要量子器件可以很好的屏蔽环境的影响,从而得到较长的退相干时间。
在量子计算机中,都会存在量子信息的传输过程,而作为传输信息的通道——量子数据总线(data bus)长的退相干时间,同时他也应该具备远程传输的能力,即遥远两个量子比特间的信息传输应具备良好的保真度。也就是说,这样的data bus应该尽可能的屏蔽环境的影响,同时它作为量子比特的“环境”不应该耗散掉量子比特的信息——量子比特的信息不会残留在data bus中。这里,我们就要介绍一种具有这样性质基于自旋1/2系统的data bus,它可以实现两个远程量子比特的传输。
 |
 |
 |
 |
图4展示了有效耦合随梯子长度的变化关系。
参考文献
[1] 李正中《固体理论》 (第二版) 62-89,152-219.
[2] S. Sachdev, Quantum Phase Transitions 240-272.
[3] Y. Li, T. Shi. B. Chen, Z. Song and C. P. Sun, Phys. Rev. A 71,022301 (2005).
[4] Y. Makhlin, G. Schön, and A. Shnirman, Rev. Mod. Phys. 73, 357 (2001).

 前一篇文章
前一篇文章 下一篇文章
下一篇文章![[講座] 星際效應,有影無?-CASE電影科普講座](http://highscope.ch.ntu.edu.tw/wordpress/wp-content/uploads/2014/12/星際效應宣傳圖-620x280.gif) [講座] 星際效應,有影無?-CASE電影科普講座
[講座] 星際效應,有影無?-CASE電影科普講座  2015年觀星大事記
2015年觀星大事記  斯特凡-波茲曼定律
斯特凡-波茲曼定律  【2013諾貝爾獎特別報導】物理獎:終於,來到了!
【2013諾貝爾獎特別報導】物理獎:終於,來到了!  【特別報導】2013年諾貝爾獎預測(二)物理獎
【特別報導】2013年諾貝爾獎預測(二)物理獎  玻色-愛因斯坦分布
玻色-愛因斯坦分布  馬克士威-波茲曼分布
馬克士威-波茲曼分布 ![[講義] 科學史沙龍:陳竹亭教授、楊信男教授](http://highscope.ch.ntu.edu.tw/wordpress/wp-content/uploads/2015/01/科學史.png) [講義] 科學史沙龍:陳竹亭教授、楊信男教授
[講義] 科學史沙龍:陳竹亭教授、楊信男教授 


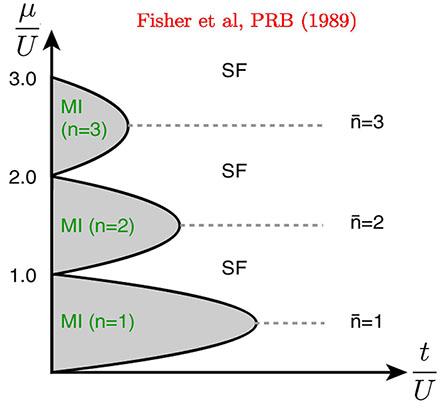 举个具体的例子吧. 例子很简单, 不是我自己的...这个具体的例子是计算石墨烯的能带结构. Level 1你在固体物理课上学会了紧束缚近似算能带: 写出最近邻的紧束缚 Hamiltonian: H=-\sum_{\langle\i,j\rangle}t (c_{A,i}^\dagger c_{B,j}+\mathrm{h.c.}), 做完 …
举个具体的例子吧. 例子很简单, 不是我自己的...这个具体的例子是计算石墨烯的能带结构. Level 1你在固体物理课上学会了紧束缚近似算能带: 写出最近邻的紧束缚 Hamiltonian: H=-\sum_{\langle\i,j\rangle}t (c_{A,i}^\dagger c_{B,j}+\mathrm{h.c.}), 做完 …
共鳴箱(如小提琴、吉他),如何與這麼多的音共振?這些音與音的頻律並非都是簡單的倍數關係(12音律, Do:523Hz,Re:587Hz)。
另外,一個樂器發出的音(如直笛所吹出的Do),因除了基音外,還有其他的泛音。那我們所謂的音諧是指基音嗎?看過其他資料顯示,基音有時並非音量最大的音(如橫笛最大音量是第一泛音,單簧管最大音量是第四泛音)。
謝謝!祝教安!