http://www.physixfan.com/archives/386
庞加莱的几何学
作者： physixfan 最近在看庞加莱（Poincaré）（又被翻译成彭加勒）的《科学与假设》，这是一本闪耀着思想光辉的圣书。介绍科学知识的书很多很多，但是像《科学与假设》这种写科学哲学的书恐怕很难找得到。虽然这本书的语言非常艰涩难懂，但这本书我至少读过3遍，每一遍都能读出一些新的感悟。
在这本书里，庞加莱对几何学提出了几条思想很深刻的见解：
1.几何学公理既非综合判断，也非实验经验，他们是约定。约定是心智的产物，约定的选择是自由的，但又不是随意的。
2.假使自然界没有固体，便不会有几何学。欧几里德几何学的性质与天然固体非常符合。
3.欧几里德几何学不比非欧几何学更真，他只是更为方便而已。经验在任何时候都不会与欧几里德共设相矛盾，同样任何经验永远也不会和罗巴切夫斯基共设相矛盾。
4.可以建立一本词典，把非欧几何的术语和欧几里德几何的术语之间建立一一对应的关系，这样非欧几何将永远不会和欧几里德几何相矛盾。
5.实验告诉我们的是物体之间的相互关系；至于物体与空间的关系，或者空间个部分的互相关系，没有一个实验影响或者能够影响。实验与空间无关，而与物体有关。
为了对非欧几何加以诠释，庞加莱在这本书里提到了著名的庞加莱圆盘模型，这个模型是非常有意思的：
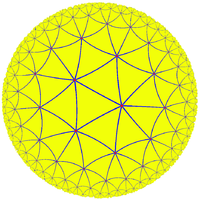
假定有一个用大球包围起来的世界，他服从下述定律：（1）温度不是均匀的，在中心温度最高，随着距中心距离的增大，温度成比例的减小，当接近包围这个世界的球面时，温度降至绝对零度。更精确的表述为：设R为包围这个世界的球的半径，r是所考虑的点到中心的距离，则绝对温度将与R^2-r^2成正比。（2）这个世界上一切物体具有同一膨胀系数，从而任何量尺的长度都与他的绝对温度成比例。（3）假定一物体从一点移动到另一点时，他能立即与新环境处于热平衡。（4）这个世界充满了光的折射媒介质，折射率与R^2-r^2成反比。以上这些假设，没有什么是矛盾的或不可想象的。直观的图形可以参见左图。这就是非欧几何的一种。
从我们通常的几何学观点来看，这个世界是有限的，但对于这个世界的居民来说，它却是无限的。因为当居民试图接近有限球面时，他们逐渐变冷因而变得越来越小，他们迈出的步子越来越小从而永远达不到有限球面。
由假定（1）可以推算出来在这个世界中最短路径不是直线，而是圆弧，这圆弧将垂直于边界。假定（4）则保证了光的物理性质：光总走光程最短的路线，从而保证这个世界的居民对光的研究和对固体的研究是一致的。
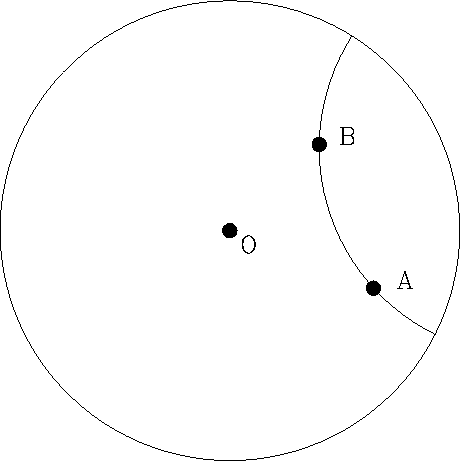
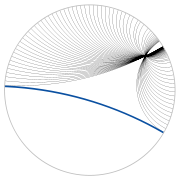
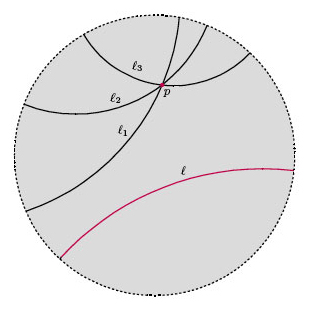
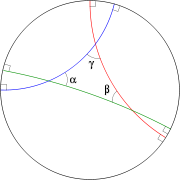
说这个世界是非欧几何，最主要的证据是它违反了欧几里德的第五共设。注意，在庞加莱模型中过“直线”外一点可以做出无数条与该直线平行的“直线”。为了搞清楚这句话的确切意思，我们需要明确一下“直线”的定义，“直线”指的是过两点的最短路径，所以在此模型中“直线”就是连接两点并且垂直于边界的圆弧。
还应该注意，在这个模型中三角形的内角和小于180度。
最后，再放一张我在这篇文章中提到过的艺术家埃舍尔的画作《天使与魔鬼》，这幅画中的天使和魔鬼就处在庞加莱圆盘模型当中。
好了，就写这么多吧，好久没有这么认真的写一篇文章了。
在这本书里，庞加莱对几何学提出了几条思想很深刻的见解：
1.几何学公理既非综合判断，也非实验经验，他们是约定。约定是心智的产物，约定的选择是自由的，但又不是随意的。
2.假使自然界没有固体，便不会有几何学。欧几里德几何学的性质与天然固体非常符合。
3.欧几里德几何学不比非欧几何学更真，他只是更为方便而已。经验在任何时候都不会与欧几里德共设相矛盾，同样任何经验永远也不会和罗巴切夫斯基共设相矛盾。
4.可以建立一本词典，把非欧几何的术语和欧几里德几何的术语之间建立一一对应的关系，这样非欧几何将永远不会和欧几里德几何相矛盾。
5.实验告诉我们的是物体之间的相互关系；至于物体与空间的关系，或者空间个部分的互相关系，没有一个实验影响或者能够影响。实验与空间无关，而与物体有关。
为了对非欧几何加以诠释，庞加莱在这本书里提到了著名的庞加莱圆盘模型，这个模型是非常有意思的：
假定有一个用大球包围起来的世界，他服从下述定律：（1）温度不是均匀的，在中心温度最高，随着距中心距离的增大，温度成比例的减小，当接近包围这个世界的球面时，温度降至绝对零度。更精确的表述为：设R为包围这个世界的球的半径，r是所考虑的点到中心的距离，则绝对温度将与R^2-r^2成正比。（2）这个世界上一切物体具有同一膨胀系数，从而任何量尺的长度都与他的绝对温度成比例。（3）假定一物体从一点移动到另一点时，他能立即与新环境处于热平衡。（4）这个世界充满了光的折射媒介质，折射率与R^2-r^2成反比。以上这些假设，没有什么是矛盾的或不可想象的。直观的图形可以参见左图。这就是非欧几何的一种。
从我们通常的几何学观点来看，这个世界是有限的，但对于这个世界的居民来说，它却是无限的。因为当居民试图接近有限球面时，他们逐渐变冷因而变得越来越小，他们迈出的步子越来越小从而永远达不到有限球面。
由假定（1）可以推算出来在这个世界中最短路径不是直线，而是圆弧，这圆弧将垂直于边界。假定（4）则保证了光的物理性质：光总走光程最短的路线，从而保证这个世界的居民对光的研究和对固体的研究是一致的。
说这个世界是非欧几何，最主要的证据是它违反了欧几里德的第五共设。注意，在庞加莱模型中过“直线”外一点可以做出无数条与该直线平行的“直线”。为了搞清楚这句话的确切意思，我们需要明确一下“直线”的定义，“直线”指的是过两点的最短路径，所以在此模型中“直线”就是连接两点并且垂直于边界的圆弧。
还应该注意，在这个模型中三角形的内角和小于180度。
最后，再放一张我在这篇文章中提到过的艺术家埃舍尔的画作《天使与魔鬼》，这幅画中的天使和魔鬼就处在庞加莱圆盘模型当中。
好了，就写这么多吧，好久没有这么认真的写一篇文章了。
Happy Day: 龐加萊猜想（Poincare Conjecture）
happyday-happyday.blogspot.com/2010/03/poincare-conjecture.html
2010年3月22日 - 迄今他仍不打算將其破解龐加萊猜想的解答，正式在科學期刊上發表。由於在權威 ... 該研究所今年6月將與龐加萊研究所，在巴黎舉辦一場會議，慶祝龐加萊猜想得以破解。 龐加萊 ... 假如兩者有明顯的溫度差，我們稱為冷鋒。 空氣由 ...科科史上的今天- 【科學史上的今天】04/29——龐加萊誕辰 ...
history.pansci.tw/post/117644254476/04-29-jules-henri-poincare
6 days ago - 【科學史上的今天】04/29——龐加萊誕辰（Jules Henri Poincaré, 1854—1912）. 從十九世紀末到二十世紀初的世紀交替之際，出現許多極具天賦之 ...[PDF]PDF檔
psroc.phys.ntu.edu.tw/bimonth/download.php?d=1&cpid=206...
至今只有一題被解答出來，即是所謂的龐加萊猜想 ... 這個猜想是龐加萊（Jules Henri Poincaré）獨創的. 概念。龐加 ... 就像熱流會使不規則的溫度分佈變得均勻，瑞.相对论通俗演义第六章狭义相对论 - 原子与分子物理研究所
iamp.jlu.edu.cn/news_list2.php?id=105
轉為繁體網頁
庞加莱得到了lorentz 变换，希尔伯特在爱因斯坦之前得到了正确的广义相对论场方程。 ... 但poincare 似乎是完全接受不了爱因斯坦的狭义相对论，虽然两个人的结果是 .... 假如是非线性的变换，就可能把一个没有零温度的惯性参考系变成一个热辐射的 ...轉為繁體網頁
庞加莱的几何学- 宇宙的心弦| 宇宙的心弦
www.physixfan.com/archives/386
轉為繁體網頁
2009年2月21日 - 最近在看庞加莱（Poincaré）（又被翻译成彭加勒）的《科学与假设》，这是一 ... 假定有一个用大球包围起来的世界，他服从下述定律：（1）温度不是均匀 ...轉為繁體網頁
庞加莱截面(Poincare surface of section)由Poincare于十九世纪末提出，用来对多变量自治系统的运动进行分析。
2基本思想编辑
其基本思想是在多维相空间(x,,dx, ldt,xZ,d²x /dt²,...dR /dt)中适当选取一截面，在此截面上某一对共扼变量如x dx, ldt取固定值，称此截面为Poincar截面。
观测运动轨迹与此截面的截点( Poincare点)，设它们依次为P1,P2,P3…。原来相空间的连续轨迹在Poincare截面上便表现为一些离散点之间的映射Pn。由它们可得到关于运动特性的信息。如不考虑初始阶段的暂态过渡过程，只考虑Poincare截面的稳态图像，当Poincare截面上只有一个不动点和少数离散点时，可判定运动是周期的;当Poincare截面上是一封闭曲线时，可判定运动是准周期的;当Poincare截面上是成片的密集点，且有层次结构时，可判定运动处于混沌状态。
Saturday, January 24, 2015
高斯绝妙定理指出，这片披萨必须有至少一个方向永远保持平整——不管你怎么弯，它一定会留下一点“平”的痕迹。
http://www.guokr.com/article/439344/
高斯绝妙定理指出，这片披萨必须有至少一个方向永远保持平整——不管你怎么弯，它一定会留下一点“平”的痕迹。
相反，鸡蛋壳两个方向上都是弯的。这是它的关键。用数学语言表达，那就是这些双重弯曲的曲面拥有非零的高斯曲率。像我们先前遇到的橘子皮一样，这意味着它们不可能被压平，除非有撕裂或者拉伸——有高斯绝妙定理保证这一点。要打破一个鸡蛋，你必须首先弄出一个坑。等到鸡蛋失去了弯曲，也就失去了强度
数学
（Ent/编译）我们都遇到过这种情况。你抓起一块披萨，正要一口吞掉的时候，披萨一下子软了，从你的指尖处耷拉了下来。披萨饼本身的结构强度不够高，无法支持整片的重量。也许下次应该少加点儿料？不用，无需绝望。
如果是是个吃披萨多年的老手，那你应该知道怎么对付这样的场景：只需把披萨弯成U形即可。（手头没有披萨？拿一张纸试验一下就好。）
一张纸拿在手里就会耷下去，但弯曲握就能让它笔直。为什么呢？图片来源：Aatish Bhatia
这个披萨小窍门的背后，深藏着一项关于曲面的强力数学。这一数学发现如此绝妙，以至于它的发明人——数学天才卡尔·弗雷德里克·高斯（Carl Friedrich Gauss）——给它起了个拉丁文名叫Theorema Egregium，意思是“绝妙定理”。
拿一张纸，卷成圆柱形纸筒。你可能觉得显而易见，纸本来是平的，卷成筒就弯了，对吧？可是高斯不这么想。他想给纸的弯曲程度（“曲率”）下一个定义，让它不因你人工施加的弯曲而改变。
图片来源：Aatish Bhatia
如果你放大去看一只生活在纸筒上的蚂蚁，这只蚂蚁可以走很多条不同的路线。它可以沿着弯曲道路横着走下去，画出一个圆；也可以沿着平坦路线竖着走，走出一条直线。或者它可以把两种方式组合起来，走一条螺旋。
高斯的天才在于，他想到把所有这些路线都纳入曲率定义里面。办法是这样的：从任何一点出发，找到这只蚂蚁能选择的最极端的两条路线——也就是最凹的和最凸的两条线。然后把它们的曲率乘起来。凸的路线曲率是正的，凹的路线曲率是负的，直的路线曲率是0。你得到的数字，就是那个点上的高斯曲率。
图片来源：Aatish Bhatia
举几个例子吧。对于纸筒上的蚂蚁来说，最极端的两条路，一条是横着画圆，另一条就是竖着画直线。但是因为直线具有0曲率，所以乘起来总是得到0。照数学家的说法，纸筒是平的——它的高斯曲率就是0。这正是因为你能用平整的纸张卷出一个纸筒。
相反，如果蚂蚁活在一个球上，那么它就无法找到平坦的路线，每一条道路都会有一定程度的向外凸出，所以高斯曲率一定是个正的数。所以，球是弯的，而筒是平的。你可以把一张纸卷成一个筒，却永远不能卷成一个球。
图片来源：Aatish Bhatia
高斯的绝妙定理就是：生活在曲面上的蚂蚁，根本不需要离开它就能知道曲面的曲率。只要测量一下距离，计算一下就行。顺便说，这也是为什么我们没有离开宇宙却能测量出我们的宇宙是不是平的（根据目前的观测来看，它是）。
但这个定理还有一个绝妙的结果：你可以随意弯曲一个曲面，只要你不拉长、压缩或者撕裂它，高斯曲率一定不会变。因为单纯弯曲不改变其上的距离，所以不管怎么弯，上面的蚂蚁总会计算出同样的高斯曲率。
听起来可能有点儿抽象，但是这推论有十分紧贴现实的结果。把一个橘子切成两半，吃掉里面的东西，然后把剩下半个橘子皮放在地上，踩吧。皮永远不可能被踩扁成一个完整的圆。相反，它一定会裂开。这是因为球面和平面拥有不同的高斯曲率，所以不扭曲、不撕裂，是不可能把球面压平的。有没有试过给人寄篮球当礼物？包装纸会遇到完全一样的问题。不管你怎么弯曲一张纸，它总会留下一点点“平”的痕迹，所以最后只能得到皱皱巴巴一团糟。
桔子皮不可能压成完整圆——因为球面和平面高斯曲率不同（而且桔子皮也没有什么延展性）。图片来源：Aatish Bhatia
这个定理的另一个推论是，平面纸上永远不可能画出准确的地图。很多常见世界地图投影方式能精确地保留角度，但是在面积上就有严重误差。数学博物馆的推特指出，服装设计师也面临类似挑战——他们在平面上设计花样，却要符合弯曲的人体。
每个红色圆圈的实际面积是相等的，但在地图上看起来就有很大的差异。图片来源：Stefan Kühn (左), Eric Gaba (右) / Wikimedia
那这一切和披萨饼有什么关系呀？是这样的：你拿起披萨之前，它是平的（数学上说，它的高斯曲率为0）。高斯绝妙定理指出，这片披萨必须有至少一个方向永远保持平整——不管你怎么弯，它一定会留下一点“平”的痕迹。当这片披萨塌下去的时候，平的方向（红色箭头）是朝侧面的，这对吃掉它可没有什么帮助。但是如果你抢在它塌下去之前，先把披萨侧着捏弯，就迫使另一个方向只能保持平整——也就是对着你嘴巴的方向。还真是绝妙的定理呀。
没想到几何学也能这么美味吧。图片来源：Aatish Bhatia
在一个方向上弯曲，来迫使它在另一个方向上保持平直。一旦你理解了这个点子，你就会到处都看到它。仔细看看一片草叶。它通常都是沿着中央叶脉弯曲的，这能帮助它维持笔直，不会软塌下去。工程师经常用弯曲来强化结构承载力。在马德里扎祖拉体育场，西班牙结构工程师埃杜拉多·托罗亚（Eduardo Torroja）设计了一套创新的混凝土屋顶，从边缘一直伸到看台上方，遮蔽了大片区域，而厚度只有几厘米。这其实就是披萨技巧。
弯曲的草叶。图片来源：Dudley Carr / Flickr
西班牙扎祖拉体育场。图片来源：Ximo Michavila
弯曲带来力量。想想看：你能站在一个空易拉罐上，它能轻松承载你的体重；可是易拉罐外壁的厚度差不多和纸一样薄。它的秘密就是它的弯曲。如果有人趁你站在上面的时候拿笔戳一下易拉罐，就能戏剧化地展现这一点——只需一个小凹坑，它就会在你脚下轰然崩塌。
纸板箱里隐藏的秘密。图片来源：Craig Sunter / Flickr
但最日常的例子可能是无处不在的波形建材。世界上简直没有比纸板箱更无聊的东西，但是撕开一个这样的箱子，你会看到箱壁里一条熟悉的波浪曲线。这些皱褶在里面可不是为了好看，它们是一种天才的结构方式：让材料又薄又轻，又能坚硬到足以承担可观的重压。
很多人小时候玩过的把戏：把一张纸折叠几次就能承载很大的重量，但它背后的数学可能你就想不到了。图片来源：Aatish Bhatia
波形金属板使用的也是同样的原理。这些不起眼的建材是纯实用性的体现，它们的形态和其功能完美契合；它们的高强度和相对低廉造价使其成为了整个现代世界的背景。
今天，我们就算看到这些波浪形金属板也几乎不会多想什么。但当它们诞生时，许多人把波形建材看成是奇迹材料。1829年，亨利·帕尔默（Henry Palmer）获得了波形建材的专利，他是一个英国工程师，负责建造伦敦码头。帕尔默建起了世界上第一个波形钢结构建筑——伦敦码头的松油棚屋。虽然它今天看来可能没什么了不起，但是听听当时的一家建筑学杂志是怎么描述它的吧：
虽然波形建材和易拉罐的强度可以很高，但有个办法让这些材料变得更强。想自己找到这个办法？去冰箱拿个鸡蛋出来。放在掌心，整只手握住鸡蛋，挤吧。（尝试这个的时候记得别戴戒指。）你会为它的强度而惊讶的。我就没法把鸡蛋握坏，哪怕用尽全力也没戏。（真的，谁试谁知道。）
请务必在家中尝试一下——好吧，为了安全，别在电脑前尝试。图片来源：Aatish Bhatia
鸡蛋为什么这么强？易拉罐和波形金属板在一个方向上是弯的，另一个还是平的。这一弯曲让它们拥有了一定强度，但它们还是有可能被压成本来的平板。
相反，鸡蛋壳两个方向上都是弯的。这是它的关键。用数学语言表达，那就是这些双重弯曲的曲面拥有非零的高斯曲率。像我们先前遇到的橘子皮一样，这意味着它们不可能被压平，除非有撕裂或者拉伸——有高斯绝妙定理保证这一点。要打破一个鸡蛋，你必须首先弄出一个坑。等到鸡蛋失去了弯曲，也就失去了强度。
图片来源：Owen Cliffe / Wikimedia
核电站冷却塔的象征性形状也在两个方向上利用了弯曲。这个形状叫做双曲面，能让所需的材料最少。正常的烟囱很像巨大易拉罐——结实是结实，但是很容易弯。双曲面形状的烟囱靠双向弯曲来解决这个问题，这样的弯曲方式能把形状“锁死”在空间中，提供额外的强度。
另一种得益于弯曲的形状是品客“薯片”，照数学家的说法，这是个双曲抛物面（hyperbolic paraboloid，舌头打结了没？）。
图片来源：Aatish Bhatia
自然界运用这一形状的招数堪称脑洞大开。濑尿虾有一项臭名昭著的本领——动物界里最快的拳击手，它的一拳打出去的力道足以把着力点上的水蒸发掉，创造出冲击波和闪光。要想使出这死亡一击，濑尿虾使用了双曲抛物面形状的“弹簧”。平时它把弹簧压缩起来储存巨大的能量，然后一招之内释放出来。
西班牙-墨西哥建筑师菲利克斯·坎德拉（Félix Candela）很懂薯片形状的力量。坎德拉是托罗亚的学生，他的建筑将双曲抛物面带到了新的高度（字面意思）。当你听到“混凝土”这个词的时候，恐怕只会想到无聊透顶的方块建筑，但坎德拉却利用双曲抛物面盖起了巨大的建筑，使用的混凝土薄到不可思议。身为这一材料的真正大师，他既是极富创新的建筑者，也是结构艺术家。
图片来源：Ciudad de las Artes y las Ciencias / Flickr
所以为什么薯片形状强度如此之高？这和它平衡张力与压力的方式有关。一切建筑都要支撑重量，最终将这些重量传递到地面上。这一传递可以靠两种不同方式完成：其一是压缩，拱顶就是纯靠压力而实现的例子；另一个就是拉伸，把一根锁链拎起来，它的每一环就都处于拉伸状态、受到张力。双曲抛物面结合了两种方式的优点。凹下去的U型部分处于拉伸状态，而凸起来的拱顶部分则是压缩，高斯绝妙定理则保证了任何一个地方的受力都会传递到四周——因为这是一个高斯曲率非零的曲面。只要你试图改变它的形状，就必须得连带压缩或者拉伸一整片区域才能让结果遵从高斯的律令；像纸张那样只弯曲一条线而不影响其他部分是不可能的。通过这样的双重弯曲，这一形状实现了张力和压力之间的精妙平衡，让它以很小的厚度就能实现惊人的强度。
通过弯曲来产生强度，这个想法塑造了我们所见的当代世界，而它的根源却来自万古不变的几何学。所以下一次你抓起一块披萨的时候，记得朝周围看看，欣赏一下这个简单的披萨小把戏背后的庞大遗产吧。（编辑：Calo）
高斯绝妙定理指出，这片披萨必须有至少一个方向永远保持平整——不管你怎么弯，它一定会留下一点“平”的痕迹。
相反，鸡蛋壳两个方向上都是弯的。这是它的关键。用数学语言表达，那就是这些双重弯曲的曲面拥有非零的高斯曲率。像我们先前遇到的橘子皮一样，这意味着它们不可能被压平，除非有撕裂或者拉伸——有高斯绝妙定理保证这一点。要打破一个鸡蛋，你必须首先弄出一个坑。等到鸡蛋失去了弯曲，也就失去了强度
数学
你拿披萨的方式，很可能是错的
高斯 曲面 曲率 平面 几何 几何学 空间 建筑 波形 建材 弯曲 波纹 强度 张力 拉力 双曲 抛物 受力
Aatish Bhatia 发表于 2014-10-17 17:30
（Ent/编译）我们都遇到过这种情况。你抓起一块披萨，正要一口吞掉的时候，披萨一下子软了，从你的指尖处耷拉了下来。披萨饼本身的结构强度不够高，无法支持整片的重量。也许下次应该少加点儿料？不用，无需绝望。
如果是是个吃披萨多年的老手，那你应该知道怎么对付这样的场景：只需把披萨弯成U形即可。（手头没有披萨？拿一张纸试验一下就好。）
一张纸拿在手里就会耷下去，但弯曲握就能让它笔直。为什么呢？图片来源：Aatish Bhatia拿一张纸，卷成圆柱形纸筒。你可能觉得显而易见，纸本来是平的，卷成筒就弯了，对吧？可是高斯不这么想。他想给纸的弯曲程度（“曲率”）下一个定义，让它不因你人工施加的弯曲而改变。
图片来源：Aatish Bhatia高斯的天才在于，他想到把所有这些路线都纳入曲率定义里面。办法是这样的：从任何一点出发，找到这只蚂蚁能选择的最极端的两条路线——也就是最凹的和最凸的两条线。然后把它们的曲率乘起来。凸的路线曲率是正的，凹的路线曲率是负的，直的路线曲率是0。你得到的数字，就是那个点上的高斯曲率。
图片来源：Aatish Bhatia相反，如果蚂蚁活在一个球上，那么它就无法找到平坦的路线，每一条道路都会有一定程度的向外凸出，所以高斯曲率一定是个正的数。所以，球是弯的，而筒是平的。你可以把一张纸卷成一个筒，却永远不能卷成一个球。
图片来源：Aatish Bhatia但这个定理还有一个绝妙的结果：你可以随意弯曲一个曲面，只要你不拉长、压缩或者撕裂它，高斯曲率一定不会变。因为单纯弯曲不改变其上的距离，所以不管怎么弯，上面的蚂蚁总会计算出同样的高斯曲率。
听起来可能有点儿抽象，但是这推论有十分紧贴现实的结果。把一个橘子切成两半，吃掉里面的东西，然后把剩下半个橘子皮放在地上，踩吧。皮永远不可能被踩扁成一个完整的圆。相反，它一定会裂开。这是因为球面和平面拥有不同的高斯曲率，所以不扭曲、不撕裂，是不可能把球面压平的。有没有试过给人寄篮球当礼物？包装纸会遇到完全一样的问题。不管你怎么弯曲一张纸，它总会留下一点点“平”的痕迹，所以最后只能得到皱皱巴巴一团糟。
桔子皮不可能压成完整圆——因为球面和平面高斯曲率不同（而且桔子皮也没有什么延展性）。图片来源：Aatish Bhatia每个红色圆圈的实际面积是相等的，但在地图上看起来就有很大的差异。图片来源：Stefan Kühn (左), Eric Gaba (右) / Wikimedia没想到几何学也能这么美味吧。图片来源：Aatish Bhatia弯曲的草叶。图片来源：Dudley Carr / Flickr西班牙扎祖拉体育场。图片来源：Ximo Michavila纸板箱里隐藏的秘密。图片来源：Craig Sunter / Flickr很多人小时候玩过的把戏：把一张纸折叠几次就能承载很大的重量，但它背后的数学可能你就想不到了。图片来源：Aatish Bhatia今天，我们就算看到这些波浪形金属板也几乎不会多想什么。但当它们诞生时，许多人把波形建材看成是奇迹材料。1829年，亨利·帕尔默（Henry Palmer）获得了波形建材的专利，他是一个英国工程师，负责建造伦敦码头。帕尔默建起了世界上第一个波形钢结构建筑——伦敦码头的松油棚屋。虽然它今天看来可能没什么了不起，但是听听当时的一家建筑学杂志是怎么描述它的吧：
不久前路过伦敦码头时，我们十分满意地发现，帕尔默先生新发明的屋顶已经得到了实际应用。……任何一个目光敏锐的人，路过的时候都不可能不被它的优雅和简洁所打动（虽然它只是个棚屋）；而只要稍加思索，他们就会相信这一建筑的效率之高、经济之节约。我们认为，这是自亚当诞生以来，人类之手所建造的最轻又最结实（以其重量而言）的屋顶。若我们仔细观察（我们为了这一目的而爬过了各式各样的粘稠松油罐），会发现这一屋顶的总厚度绝对没有超过十分之一英寸！
这年头的建筑学杂志真是大不如前了啊。虽然波形建材和易拉罐的强度可以很高，但有个办法让这些材料变得更强。想自己找到这个办法？去冰箱拿个鸡蛋出来。放在掌心，整只手握住鸡蛋，挤吧。（尝试这个的时候记得别戴戒指。）你会为它的强度而惊讶的。我就没法把鸡蛋握坏，哪怕用尽全力也没戏。（真的，谁试谁知道。）
请务必在家中尝试一下——好吧，为了安全，别在电脑前尝试。图片来源：Aatish Bhatia相反，鸡蛋壳两个方向上都是弯的。这是它的关键。用数学语言表达，那就是这些双重弯曲的曲面拥有非零的高斯曲率。像我们先前遇到的橘子皮一样，这意味着它们不可能被压平，除非有撕裂或者拉伸——有高斯绝妙定理保证这一点。要打破一个鸡蛋，你必须首先弄出一个坑。等到鸡蛋失去了弯曲，也就失去了强度。
图片来源：Owen Cliffe / Wikimedia另一种得益于弯曲的形状是品客“薯片”，照数学家的说法，这是个双曲抛物面（hyperbolic paraboloid，舌头打结了没？）。
图片来源：Aatish Bhatia西班牙-墨西哥建筑师菲利克斯·坎德拉（Félix Candela）很懂薯片形状的力量。坎德拉是托罗亚的学生，他的建筑将双曲抛物面带到了新的高度（字面意思）。当你听到“混凝土”这个词的时候，恐怕只会想到无聊透顶的方块建筑，但坎德拉却利用双曲抛物面盖起了巨大的建筑，使用的混凝土薄到不可思议。身为这一材料的真正大师，他既是极富创新的建筑者，也是结构艺术家。
图片来源：Ciudad de las Artes y las Ciencias / Flickr通过弯曲来产生强度，这个想法塑造了我们所见的当代世界，而它的根源却来自万古不变的几何学。所以下一次你抓起一块披萨的时候，记得朝周围看看，欣赏一下这个简单的披萨小把戏背后的庞大遗产吧。（编辑：Calo）
参考资料
- Reid, Esmond. Understanding buildings: a multidisciplinary approach. MIT Press, 1984.
- Mornement, Adam, and Simon Holloway. Corrugated iron: building on the frontier. WW Norton & Company, 2007.
- Garlock, Maria E. Moreyra, David P. Billington, and Noah Burger. Félix Candela: engineer, builder, structural artist. Princeton University Art Museum, 2008.
编译来源
wired.com, How a 19th Century Math Genius Taught Us the Best Way to Hold a Pizza Slicewhite01 zeta01 gammacomplex01 diffgeorm01 manifold01 trading01 一张纸（2次元），纸上有A B两点，现在折 要在11次元动一下的，你动这一下被干扰可就是11次元坐标变动，更是死得惨 ; 固有时是观测者手中钟表的读数，是实际测量的时间，坐标时是四维时空坐标中的一个坐标分量（坐标时没有实际物理意义）
"角動量伪矢量"）【位移】【时空曲率】
为从初位置到末位置的有向线段,其大小与路径无关，方向由起点指向终点。
11次元的位移依旧是位移！ 不过是x y z 变多了
高维度位移 大家可以想向一张纸（2次元），纸上有A B两点，现在折（可以不真折 弯个弧一样）几（一）下，使A B重合。很轻松吧，具体怎么折有多种方法。折好之后再从A到B就不用在纸上走好远了。
同理，3次元的瞬间移动只要扭曲3维空间，使起点和终点重合，之后一步就可以跨过好远。不过扭曲空间的程度（时空曲率）是矢量。你敢让一方碰到这个弯折，就等死吧。而且你还是要在11次元动一下的，你动这一下被干扰可就是11次元坐标变动，更是死得惨
11次元的位移依旧是位移！ 不过是x y z 变多了
高维度位移 大家可以想向一张纸（2次元），纸上有A B两点，现在折（可以不真折 弯个弧一样）几（一）下，使A B重合。很轻松吧，具体怎么折有多种方法。折好之后再从A到B就不用在纸上走好远了。
同理，3次元的瞬间移动只要扭曲3维空间，使起点和终点重合，之后一步就可以跨过好远。不过扭曲空间的程度（时空曲率）是矢量。你敢让一方碰到这个弯折，就等死吧。而且你还是要在11次元动一下的，你动这一下被干扰可就是11次元坐标变动，更是死得惨
爱lixiufei123: 众所周知，狭义相对论中定义的“固有时间“Δτ 在洛伦兹变换中保持不变，属于标量。静坐标系中“固有时间“Δτ 表示这个物理过程发生的时间量；动坐标系中Δt表示物理过程发生的时间量。那么，“固有时间“Δτ在动坐标系中有什么物理意义呢？
2013-10-5 05:06回复
还有2条回复，点击查看
No comments:
Post a Comment