
二次型與正定矩陣
本文的閱讀等級:中級
設![A=[a_{ij}] A=[a_{ij}]](https://s0.wp.com/latex.php?latex=A%3D%5Ba_%7Bij%7D%5D&bg=ffffff&fg=000000&s=0) 為
為 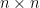 階實矩陣,
階實矩陣, 為
為  維實向量,具有以下形式的實函數稱為二次型 (quadratic form):
維實向量,具有以下形式的實函數稱為二次型 (quadratic form):
 正定矩陣的概念建立於二次型之上。若
正定矩陣的概念建立於二次型之上。若  是一實對稱矩陣且任一
是一實對稱矩陣且任一  滿足
滿足  ,我們稱
,我們稱  是正定的,詳細內容請參見“特殊矩陣 (6):正定矩陣”。
是正定的,詳細內容請參見“特殊矩陣 (6):正定矩陣”。
任意二次型 都可以轉換為等價的
都可以轉換為等價的  ,
, 是實對稱矩陣。利用一點運算技巧改寫矩陣乘法公式可得
是實對稱矩陣。利用一點運算技巧改寫矩陣乘法公式可得
![\begin{aligned}\displaystyle \mathbf{x}^TA\mathbf{x}&=\sum_{i,j=1}^na_{ij}x_ix_j\\ &=\sum_{i,j=1}^n\frac{1}{2}(a_{ij}+a_{ji})x_ix_j\\ &=\mathbf{x}^T\left[\frac{1}{2}(A+A^T)\right]\mathbf{x}^T\end{aligned} \begin{aligned}\displaystyle \mathbf{x}^TA\mathbf{x}&=\sum_{i,j=1}^na_{ij}x_ix_j\\ &=\sum_{i,j=1}^n\frac{1}{2}(a_{ij}+a_{ji})x_ix_j\\ &=\mathbf{x}^T\left[\frac{1}{2}(A+A^T)\right]\mathbf{x}^T\end{aligned}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Baligned%7D%5Cdisplaystyle++%5Cmathbf%7Bx%7D%5ETA%5Cmathbf%7Bx%7D%26%3D%5Csum_%7Bi%2Cj%3D1%7D%5Ena_%7Bij%7Dx_ix_j%5C%5C++%26%3D%5Csum_%7Bi%2Cj%3D1%7D%5En%5Cfrac%7B1%7D%7B2%7D%28a_%7Bij%7D%2Ba_%7Bji%7D%29x_ix_j%5C%5C++%26%3D%5Cmathbf%7Bx%7D%5ET%5Cleft%5B%5Cfrac%7B1%7D%7B2%7D%28A%2BA%5ET%29%5Cright%5D%5Cmathbf%7Bx%7D%5ET%5Cend%7Baligned%7D&bg=ffffff&fg=000000&s=0) 矩陣
矩陣  和
和 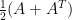 有相等的二次型,不難驗證
有相等的二次型,不難驗證 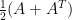 是對稱的。例如,
是對稱的。例如,
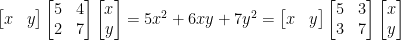 因此僅討論具對稱性的二次型已足夠應付一般的問題,這與我們習慣將對稱納入正定的定義其道理是相同的。
因此僅討論具對稱性的二次型已足夠應付一般的問題,這與我們習慣將對稱納入正定的定義其道理是相同的。
特徵值和特徵向量是線性代數裡分析矩陣結構與線性變換最重要的概念,二次型的最大化 (或最小化) 問題是特徵值和特徵向量的一個典型應用。設 是實對稱矩陣,考慮此問題:
是實對稱矩陣,考慮此問題:
最大化 ,
, 滿足
滿足 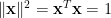 。
。
求解這個約束最佳化 (constrained optimization) 問題的傳統方法是引入 Lagrangian 函數:
 產生極值的必要條件是
產生極值的必要條件是  對
對  的各元的一次偏導數都等於零,亦即
的各元的一次偏導數都等於零,亦即  是
是  的一個駐點 (參見“最佳化理論與正定矩陣”),因為
的一個駐點 (參見“最佳化理論與正定矩陣”),因為 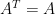 ,請讀者自行計算驗證
,請讀者自行計算驗證
 單位向量 (unit vector)
單位向量 (unit vector)  要使
要使 最大化的必要條件即為特徵方程式
最大化的必要條件即為特徵方程式 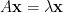 ,將此式代入二次型可得
,將此式代入二次型可得
 由於實對稱矩陣的特徵值必為實數,使二次型最大化的向量
由於實對稱矩陣的特徵值必為實數,使二次型最大化的向量  正是對應最大特徵值的特徵向量。
正是對應最大特徵值的特徵向量。
另一方面,我們也可以直接利用對稱矩陣是正交可對角化此性質來分解二次型。設 ,其中
,其中  是正交特徵向量矩陣,
是正交特徵向量矩陣,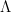 是主對角特徵值矩陣,令
是主對角特徵值矩陣,令  ,二次型可利用主對角分解化簡為
,二次型可利用主對角分解化簡為
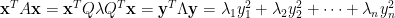 因為
因為 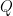 是正交矩陣,
是正交矩陣, (見“特殊矩陣 (3):么正矩陣(酉矩陣)”),由此亦可推論
(見“特殊矩陣 (3):么正矩陣(酉矩陣)”),由此亦可推論  的最大值即為
的最大值即為  的最大特徵值。
的最大特徵值。
統計學中的主成分分析 (principal components analysis),簡稱 PCA,是二次型最大化的典型應用。設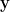 是由
是由  個隨機變數組成的向量,
個隨機變數組成的向量,
 我們沿用機率學的慣用符號,以大寫英文字母表示隨機變數,請特別注意各符號的意義勿與矩陣混淆。共變異數矩陣 (covariance matrix)
我們沿用機率學的慣用符號,以大寫英文字母表示隨機變數,請特別注意各符號的意義勿與矩陣混淆。共變異數矩陣 (covariance matrix) 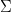 的第
的第  元定義為隨機變數
元定義為隨機變數  和
和  的共變異數或稱協方差:
的共變異數或稱協方差:
![\Sigma_{ij}=\mathrm{cov}(Y_i,Y_j)=E\left[(Y_i-\mu_i)(Y_j-\mu_j)\right] \Sigma_{ij}=\mathrm{cov}(Y_i,Y_j)=E\left[(Y_i-\mu_i)(Y_j-\mu_j)\right]](https://s0.wp.com/latex.php?latex=%5CSigma_%7Bij%7D%3D%5Cmathrm%7Bcov%7D%28Y_i%2CY_j%29%3DE%5Cleft%5B%28Y_i-%5Cmu_i%29%28Y_j-%5Cmu_j%29%5Cright%5D&bg=ffffff&fg=000000&s=0) 其中
其中 ![\mu_i=E[Y_i] \mu_i=E[Y_i]](https://s0.wp.com/latex.php?latex=%5Cmu_i%3DE%5BY_i%5D&bg=ffffff&fg=000000&s=0) 為
為  的期望值。因此
的期望值。因此  ,共變異數矩陣是對稱的,可表示為
,共變異數矩陣是對稱的,可表示為
![\Sigma={E}\left[(\mathbf{y}-{E}(\mathbf{y}))(\mathbf{y}-{E}(\mathbf{y}))^T\right] \Sigma={E}\left[(\mathbf{y}-{E}(\mathbf{y}))(\mathbf{y}-{E}(\mathbf{y}))^T\right]](https://s0.wp.com/latex.php?latex=%5CSigma%3D%7BE%7D%5Cleft%5B%28%5Cmathbf%7By%7D-%7BE%7D%28%5Cmathbf%7By%7D%29%29%28%5Cmathbf%7By%7D-%7BE%7D%28%5Cmathbf%7By%7D%29%29%5ET%5Cright%5D&bg=ffffff&fg=000000&s=0) 假設每個隨機變數的期望值為零,
假設每個隨機變數的期望值為零, ,共變異數矩陣可化簡為
,共變異數矩陣可化簡為
![\Sigma={E}[\mathbf{y}\mathbf{y}^T] \Sigma={E}[\mathbf{y}\mathbf{y}^T]](https://s0.wp.com/latex.php?latex=%5CSigma%3D%7BE%7D%5B%5Cmathbf%7By%7D%5Cmathbf%7By%7D%5ET%5D&bg=ffffff&fg=000000&s=0)
主成分分析的目的在尋找單位向量 使隨機變數向量
使隨機變數向量 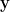 於
於  方向的投影具有最大變異量。因為
方向的投影具有最大變異量。因為 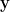 的期望值為零,
的期望值為零, 為常數向量可以提至期望值運算符號之外,就有
為常數向量可以提至期望值運算符號之外,就有
![{E}[\mathbf{x}^T\mathbf{y}]=\mathbf{x}^T{E}[\mathbf{y}]=\mathbf{x}^T\mathbf{0}=0 {E}[\mathbf{x}^T\mathbf{y}]=\mathbf{x}^T{E}[\mathbf{y}]=\mathbf{x}^T\mathbf{0}=0](https://s0.wp.com/latex.php?latex=%7BE%7D%5B%5Cmathbf%7Bx%7D%5ET%5Cmathbf%7By%7D%5D%3D%5Cmathbf%7Bx%7D%5ET%7BE%7D%5B%5Cmathbf%7By%7D%5D%3D%5Cmathbf%7Bx%7D%5ET%5Cmathbf%7B0%7D%3D0&bg=ffffff&fg=000000&s=0) 所以
所以
![\mathrm{var}\{\mathbf{x}^T\mathbf{y}\}={E}\left[(\mathbf{x}^T\mathbf{y})^2\right] \mathrm{var}\{\mathbf{x}^T\mathbf{y}\}={E}\left[(\mathbf{x}^T\mathbf{y})^2\right]](https://s0.wp.com/latex.php?latex=%5Cmathrm%7Bvar%7D%5C%7B%5Cmathbf%7Bx%7D%5ET%5Cmathbf%7By%7D%5C%7D%3D%7BE%7D%5Cleft%5B%28%5Cmathbf%7Bx%7D%5ET%5Cmathbf%7By%7D%29%5E2%5Cright%5D&bg=ffffff&fg=000000&s=0) 上式指出對於任意非零向量
上式指出對於任意非零向量  ,
, 。展開等號右側,
。展開等號右側,
![\mathrm{var}\{\mathbf{x}^T\mathbf{y}\}={E}[(\mathbf{x}^T\mathbf{y})(\mathbf{y}^T\mathbf{x})]=\mathbf{x}^T{E}[\mathbf{y}\mathbf{y}^T]\mathbf{x}=\mathbf{x}^T\Sigma\mathbf{x}\ge 0 \mathrm{var}\{\mathbf{x}^T\mathbf{y}\}={E}[(\mathbf{x}^T\mathbf{y})(\mathbf{y}^T\mathbf{x})]=\mathbf{x}^T{E}[\mathbf{y}\mathbf{y}^T]\mathbf{x}=\mathbf{x}^T\Sigma\mathbf{x}\ge 0](https://s0.wp.com/latex.php?latex=%5Cmathrm%7Bvar%7D%5C%7B%5Cmathbf%7Bx%7D%5ET%5Cmathbf%7By%7D%5C%7D%3D%7BE%7D%5B%28%5Cmathbf%7Bx%7D%5ET%5Cmathbf%7By%7D%29%28%5Cmathbf%7By%7D%5ET%5Cmathbf%7Bx%7D%29%5D%3D%5Cmathbf%7Bx%7D%5ET%7BE%7D%5B%5Cmathbf%7By%7D%5Cmathbf%7By%7D%5ET%5D%5Cmathbf%7Bx%7D%3D%5Cmathbf%7Bx%7D%5ET%5CSigma%5Cmathbf%7Bx%7D%5Cge+0&bg=ffffff&fg=000000&s=0) 推知共變量矩陣
推知共變量矩陣 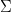 是半正定,故其特徵值皆不為負,對應
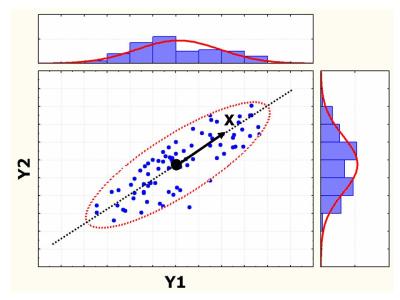
是半正定,故其特徵值皆不為負,對應 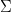 最大特徵值的特徵向量指向最大投影變異的方向,見下圖。
最大特徵值的特徵向量指向最大投影變異的方向,見下圖。
設
任意二次型
特徵值和特徵向量是線性代數裡分析矩陣結構與線性變換最重要的概念,二次型的最大化 (或最小化) 問題是特徵值和特徵向量的一個典型應用。設
最大化
求解這個約束最佳化 (constrained optimization) 問題的傳統方法是引入 Lagrangian 函數:
另一方面,我們也可以直接利用對稱矩陣是正交可對角化此性質來分解二次型。設
統計學中的主成分分析 (principal components analysis),簡稱 PCA,是二次型最大化的典型應用。設
主成分分析的目的在尋找單位向量
No comments:
Post a Comment