内坐标法是通过价键的连接关系和键长r、键角
为什么在近自由电子模型未受微扰的解中，一个波矢能够对应多个能量值？？
如题，近自由电子模型的未受微扰的解不就和量子自由电子论是一样的么？在量子自由电子论推导费米能级的过程中，认为一个波矢表示一种状态，一种状态中可以安置两个电子，并依此推导出费米能级。
然而在近自由电子模型中，由于引入了周期场近似，于是一个波矢就对应多个能量值了，这时候一个波矢不就不能表示一种状态了么，那费米能级还能适用么？明显是适用的，为什么呢？
另外，费米波矢
是否在第一布里渊区内部？若在，为何只选了
一个能量态；若不在，那又如何解释？
问题补充：近自由电子近似首先假定势能为零是的自由电子，之后加入了势能的影响，那么在加入势能影响之前，他应该就是自由电子吧。
然而在加入势能影响之前这一种情况下，如果引入了周期场近似，这时候的模型即空格子模型（注意不是近自由电子模型！！！），它的能量表达式是
，波函数是1/L^(1/2)exp[ik·r]，这时候的波失和推导费米能级的波失是一个了吧。
那么现在问题来了，为什么这个时候一个波失可以表示多种状态值呢？？周期场近似对它做了什么？
然而在近自由电子模型中，由于引入了周期场近似，于是一个波矢就对应多个能量值了，这时候一个波矢不就不能表示一种状态了么，那费米能级还能适用么？明显是适用的，为什么呢？
另外，费米波矢
问题补充：近自由电子近似首先假定势能为零是的自由电子，之后加入了势能的影响，那么在加入势能影响之前，他应该就是自由电子吧。
然而在加入势能影响之前这一种情况下，如果引入了周期场近似，这时候的模型即空格子模型（注意不是近自由电子模型！！！），它的能量表达式是
，波函数是1/L^(1/2)exp[ik·r]，这时候的波失和推导费米能级的波失是一个了吧。那么现在问题来了，为什么这个时候一个波失可以表示多种状态值呢？？周期场近似对它做了什么？
评论 (11) 只看楼主
全部评论
-
1楼 2014-10-24 13:34 浔荆 取消只看Ta
看到你的问题，回去翻了翻固体物理教材，才发现原来我的固体物理学的这么渣。[0] |
其实你的推断基本没错，从晶体模型角度出发，第一布里渊区的体积为1/V(v为正空间元胞体积，有的教材上喜欢用(2pi)^3/V，只是倒格矢单位的差别，没有本质影响)，若一个元胞内只含一个电子——注意，这点很重要——那么正好，所有电子正好把整个第一布里渊区填满。此时第一布里渊区的表面就是费米面。
但是元胞内的原子一般不会是氢原子，所以倒空间内含有n*N个电子（N为宏观晶体原子个数,n为原子序数)。此时第一布里渊区不足以放下如此多的电子，于是电子继续填充第二、第三、、、一直到第n个布里渊区，此时第n布里渊区的表面就为费米面。
再回到你的问题，为什么加了周期场近视，一个波矢就对应多个能量本征值了呢？
晶体中的多个能量本征值来自不同的布里渊区，电子填满第一布里渊区后，向其他布里渊区填充便会得到更高的能量，在波恩-卡曼边界条件下，各个布里渊区都是等价的，所以成了一个波矢的不同本征值。
如果我们把自由电子气也看成处于一个周期场下，只不过这个周期场强度处处都为0，所以周期场的周期也为0。那么此时布里渊区的体积1/V为一个无穷大的值。所以电子无论如何是填不满第一布里渊区的，此时一个波矢便只有一个能量值
- 4楼 2014-10-25 10:34 浔荆 取消只看Ta
[0] |引用@东方日月 的话：你说的都看懂了，不过怪我没表述清楚。。。。=_=。。。我问题的核心是这句话就是因为基本上之前的所有公式包括能态密度等等都是按照一个波失表示一种状态来推导的，可这时候突然告诉我一个波失可以表示好多种状态...
也怪我没有把重点说清吧。。。
周期性场下的多个能量值来自周期性边界条件下，倒空间也呈现出的周期性。也就是说，将波矢k增大一个布里渊区长度的值，体系能量本征值的大小并不改变。所以可以把第N能带理解成原本第N布里渊区内的能带，只是在周期性条件下平移到第一布里渊区了而已。
实际上，我认为没有周期场时这种平移对称性也是存在的，只不过正空间的平移周期变为0，倒空间的平移周期变为无穷大。所以——针对你的问题——在没有周期场的作用下，一个波矢也可以有很多能量本征态的。只不过这个能量值无穷大，永远不能被电子填充而已。
题外话：其实我不太喜欢能带的近自由电子近似，用紧束缚近似理解起来多形象啊。一句话就可以概括——能带结构是高度简并的原子轨道能级在周期性势场微扰下的分裂。 - 6楼 2014-10-26 08:41 浔荆 取消只看Ta
1、没错没错，就是这两张图。将第一张图做周期性的平移就得到了第二张图了，实际上两个图表达的是一个内容。
2、你指那些结论不能推倒出来呢？倒空间周期无穷大其实就等于没有周期性，这点在数学上（应当）是等价的，第二能级能量为无穷大其实也就等价于没有第二能级。所以把自由电子当做平面波来处理还是没有问题的。
【学习笔记】《计算化学-从理论化学到分子模拟》- 2 （23页~）
|||
1. Hohenberg-Kohn第一定理：多电子体系若其基态是非简并的，则该基态体系中核与电子的相互作用势能v(r)唯一的取决于体系的电子密度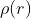
（只差了一个无关紧要的常量）
2. HK第一定理的证明：利用反证法。先假设有两种电子态密度，然后利用两种电子态的平权性质。因为只要两个物体是平权的，那么证明中一旦出现单调性的方向。那么必然会导致paradox。
问题：1. 如何证明HK第一定理（非简并情况）。2. 如何从非简并情况推广到简并情况。
3. 1968年，E.B.Wilson Jr.说：“我们相信能进一步把任何物理量的计算归结到一阶约化密度
中计算，这就是通常的三维空间中普遍意义的电子密度。” 1968年，J.R.Platt说：“干嘛30年之后我们还憋在Schrodinger方程里呢？这从来就不是为多电子体系设计的。Fermi, Pauli, Pauling没有把它当做教条。Bohr在”经典对应原理“里也没有把它当做教条。”
4. HK定理说明所有原子核的位置只能决定基态的所有性质，而不能确定激发态有何种性质。
问题：我们有哪些办法来处理激发态的情况？
5. 分子结构文件的格式可分成两类：直角坐标法、内坐标法（即Z-matrix法）。直角坐标法就是根据N个原子具有3N个空间坐标，排列成一张表格后即可。而内坐标法是通过价键的连接关系和键长r、键角
以及二面角
来表示原子核的位置的方法。内坐标中有3N-6个坐标（减去的6个为3个平动坐标和3个转动坐标）
6. 分子内坐标和直角坐标法各有各的用处，不过在能量优化的算法中内坐标法往往用较少的迭代次数就可以达到同样的能量收敛阀值。
7. 分子的势能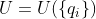
是指在无外场时单个自由分子的势能，即分子内部运动的势能，它是3N-6个核坐标
的函数（线型分子时为3N-5）。核坐标长成的空间为位形空间。同一个分子的不同结构（即位形空间中不同的点）的势能构成的曲面称为势能超曲面S，简称势能面。
8. 势能面上关心以下几种具有特殊性质的点，包括平衡点、极小点、构象、稳态点和过渡态。
平衡点：满足势能U关于核坐标qi一阶导数为0的点。包括（极小点、极大点、稳态（驻点）及过渡态）
极小点：满足平衡点条件且势能对核坐标的二次导数大于0
极大点：满足平衡点条件且势能对核坐标的二次导数小于0
稳态点（驻点）：满足平衡条件对于某一部分的核坐标二次导数大于0，而对于另一部分小于0
过渡态：满足平衡条件且只有一个方向满足二次导数小于0，而其余方向二次导数大于0。这个点称为过渡态。
9. 力场（force field）方法是一种只用于分子势能近似计算的方法。分子势能的精确计算肯定需要量子力学。
10. 假设有一个理想的“标准”分子，它具有键长r、键角、二面角都等于标准键长、标准键角以及标准二面角。且其（1》5）原子间的van der Waals能和（1》5）原子间静电能都忽略不计，这样的分子令其势能为0，也即能量零点设在这样的“标准分子”处。
http://blog.sciencenet.cn/blog-376446-758013.html 此文来自科学网何政达博客，转载请注明出处。
上一篇：【学习笔记】《计算化学-从理论化学到分子模拟》- 1
下一篇：【号外号外】冯端和金国钧的《凝聚态物理学》出齐了！
2. HK第一定理的证明：利用反证法。先假设有两种电子态密度，然后利用两种电子态的平权性质。因为只要两个物体是平权的，那么证明中一旦出现单调性的方向。那么必然会导致paradox。
问题：1. 如何证明HK第一定理（非简并情况）。2. 如何从非简并情况推广到简并情况。
3. 1968年，E.B.Wilson Jr.说：“我们相信能进一步把任何物理量的计算归结到一阶约化密度
4. HK定理说明所有原子核的位置只能决定基态的所有性质，而不能确定激发态有何种性质。
问题：我们有哪些办法来处理激发态的情况？
5. 分子结构文件的格式可分成两类：直角坐标法、内坐标法（即Z-matrix法）。直角坐标法就是根据N个原子具有3N个空间坐标，排列成一张表格后即可。而内坐标法是通过价键的连接关系和键长r、键角
6. 分子内坐标和直角坐标法各有各的用处，不过在能量优化的算法中内坐标法往往用较少的迭代次数就可以达到同样的能量收敛阀值。
7. 分子的势能
8. 势能面上关心以下几种具有特殊性质的点，包括平衡点、极小点、构象、稳态点和过渡态。
平衡点：满足势能U关于核坐标qi一阶导数为0的点。包括（极小点、极大点、稳态（驻点）及过渡态）
极小点：满足平衡点条件且势能对核坐标的二次导数大于0
极大点：满足平衡点条件且势能对核坐标的二次导数小于0
稳态点（驻点）：满足平衡条件对于某一部分的核坐标二次导数大于0，而对于另一部分小于0
过渡态：满足平衡条件且只有一个方向满足二次导数小于0，而其余方向二次导数大于0。这个点称为过渡态。
9. 力场（force field）方法是一种只用于分子势能近似计算的方法。分子势能的精确计算肯定需要量子力学。
10. 假设有一个理想的“标准”分子，它具有键长r、键角
http://blog.sciencenet.cn/blog-376446-758013.html 此文来自科学网何政达博客，转载请注明出处。
上一篇：【学习笔记】《计算化学-从理论化学到分子模拟》- 1
下一篇：【号外号外】冯端和金国钧的《凝聚态物理学》出齐了！
【学习笔记】《计算化学-从理论化学到分子模拟》- 1
|||
前言：在笔记中，如果是有人名考证的，或者证实是谁说的话，那么我就在前面用小括号表示是他本人说的话，但是书中的话就直接写上去了。大家看的时候可以这么看。这篇文章实际上是我在看书时候总结的一些笔记，写到这里与大家分享。希望能从中得到更多的讨论和反馈。希望能在科学网上和大家一起进步！
1. （序言：徐光宪先生）陈伯敏教授在新著中的一个重要理念是：只有建立针对具体研究对象的物理模型才能指明通向物质世界真理的方向，而不是普适的数学模型。
2. （前言：陈伯敏先生）对于初学者，笔者愿意传达前辈们的忠告：准备草稿纸，动笔演绎。只要是理论学科，都要反复学几遍才能得要领，不要指望听一遍就懂得个大概，不要在“自我感觉差”面前退缩，“不懂”意味着正在入门，更不要指望寓教于乐。不过在熬过长夜、豁然开朗之际，“乐”却会不期而至，那是晨曦中第一原理送来的神圣感。
3. “人们持久的希望之一就是，找到几条简单而普遍的规律，来解释具有所有表面上的复杂性和多样性的自然为什么会如此。” —— Steven Weinberg（1979 Nobel Prize）
4. 郝柏林院士：“计算物理学的目的不是计算，而是理解、语言和发现新的物理现象。”
5. 从牛顿以来的三百多年，至少是关于无生命物质世界的第一性原理的框架已经建立，这就是量子力学和统计力学。
6. 在运用第一性原理的时候，选用适当的模型才能执行计算。在这里必须强调：物理模型比数学模型重要得多，只有在暂时无法构筑物理模型的场合才不得已采用数学模型。
7. 计算化学的目的不是计算，而是理解、预言和发现新的化学现象及其物理本质。
8. 19世纪中叶Wilhem von Humboldt曾经指出：科学首先有它的自我目的，至于它的实用性，其重要意义也仅仅是第二位的。
9. 化学不应该被肢解。
我的感受：在看到这里的时候，回想了一下自己的化学知识，感觉除了电化学之外，似乎在无机、有机、分析、物化这几个方面都有欠缺，需要在后面好好的补补自己的知识。
10. 基本概念的回顾：体系、环境、体系的宏观状态和微观状态、广义坐标（广义位置）、自由度、动力学状态（力学状态）、广义动量、相空间、力学量（动力学量）、体系的宏观状态、涨落、时间平均值（与宏观测量之间的关系）、非平衡定态（稳态）、平衡态、广延量和强度量、外参量和内参量、物态方程（本构方程）、正则变量、相空间、
我的感受：这一段中所描写的基本概念大家不妨考考自己，看看真正掌握的有多少。
11. 如果体系的势能U是的体系粒子收到的力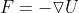
与粒子速度无关，这种力称为保守力。保守力所对应的体系称为保守体系。自然界中大部分的基本力都是保守力。对应力与速度相关的力称为非保守力，对应的体系为非保守体系。非保守力中分成两种力：耗散力和非耗散力。总是对体系做负功的力为耗散力（摩擦力），而对体系做正功的力为非耗散力（例如磁力、爆炸力）。
12. 模拟化学体系时，只要是在做看得到原子层次的模拟（所谓原子模拟，atomistic simulation），那么体系中不可能存在摩擦力，当又无外磁场存在，则总是保守系。
13. 在介观模拟（尺度为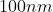
~1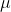
m）中，不可能作原子模拟，而是对原子经过粗粒化后作模拟，这些粗粒化的粒子之间允许出现“重叠”。于是一定含有所谓“摩擦系数”的耗散项，模拟所依据的运动方程就要从Newton方程改为Langevin方程。又如溶液体系的模拟，把研究的重点溶质做原子模拟，同时将数量极大而又不是研究重点的溶剂做连续介质近似处理，这样也要出现含有随机力项和耗散力项的Langevin方程。这类体系就属于非保守系。
14. Lagrange方程的有点在于它是关于独立变量之间的方程组，而Newton方程通常不是独立变量之间的方程组。从最小作用量原理得到Lagrange方程，而不是从Newton定律得到Lagrange方程，使得我们从单纯唯象的做法而进入力学的理性深处。
思考题：1. 什么是最小作用量原理？ 2. 如何从最小作用量原理得到Lagrange方程？（要注意吴大猷和Goldstein的变分方法的不同） 3. 如何从Lagrange方程看出Lagrange量的性质？ 4. 什么是Legendre变换？ 5. 如何利用Legendre变换从Lagrange量变成Hamilton量，进而推出Hamilton方程？ 6. 什么是m次Euler齐次函数？它有什么性质？ 7. 利用6的性质证明：在保守系的情况下，H就是体系总的机械能。对于能量守恒的体系，Hamilton函数就是体系总能量E。8. 利用最小作用原理和Hamiltonian给出Hamilton方程。 9. 推导Hamilton-Jacobi方程。 10. （没啥基本答案）说说Hamilton-Jacobi方程的意义，以及有何可以拓展的应用？
所需要的数学方法：（1）变分法，记得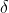
和
的交换关系 （2）Legendre变换：将函数的一部分变量变成另一部分，而变换的应该为偏导数的关系
看完第一章，大体的感觉就是：经典力学书籍的一个大概汇总，讲了最小作用原理以及Lagrangian和Hamiltonian，然后根据最小作用原理加上变分法推出来了Lagrange方程以及Hamilton方程。其实主要的目的是想让读者了解一下理论物理是如何处理问题的。从基本原理加上数学推演最后得到结论。那么化学中又是如何做的呢？第二章《势能面》会有描述。
CH2开个头：
15. “我们不说那些由基本原理推（导）不出来的话。” —— 录自喀兴林教授的《高等量子力学》，高等教育出版社1999年版，第80页
16. 本章从介绍Hohenberg-Kohn第一定理开始，在严格的量子理论的基础上建立“结构决定一切”的思想。明确了处于基态的化学体系，只要知道它们的核骨架（及分子结构），原则上就能以此为起点着手计算该体系的所有化学性质。核骨架就是位形空间中的位型，由此引出势能超曲面的概念，简称势能面。分析势能面的几何特点，尤其是其中的极小点（构象）和过渡态。
17. CH2还会介绍几种能量优化的方法：单纯形法、最速下降法、共轭梯度法、Newton-Raphson法以及寻找过渡态的几种方法。
To be continued...... 因为CH1后面都是公式推导，而我使用Latex也不是很熟练，因此先记录到这里，等有想法了再补充上去。欢迎大家及时关注！会持续更新。
http://blog.sciencenet.cn/blog-376446-757898.html 此文来自科学网何政达博客，转载请注明出处。
上一篇：【原创】电化学热力学
下一篇：【学习笔记】《计算化学-从理论化学到分子模拟》- 2 （23页~）
blog.sciencenet.cn/blog-376446-758013.html
内坐标法是通过价键的连接关系和键长r、键角以及二面角来表示原子核的位置
[PDF]球面上的測地線和一個平面幾何的問題
http://www.weibo.com/james5664?from=feed&loc=at&nick=James5664
James5664
平权博弈的盎格鲁撒克逊商业社会不是理想乌托邦，但却是迄今为止(相对西亚绿教东亚红教南欧天主教东欧正教等级社会们而言)最合理的社会了。平权博弈在当代美国也是西海岸比东海岸更公平一些下层机会更多一些，西东海岸比中部内地更公平一些下层机会更多一些。
2013年出版的《中国经济下一步》第四章粗略提了方案。第一条，重订社会契约，其实是核心。
在卢卡斯等人的早期模型中，投资者的同质假定导致了CCAPM模型尽管引入了效用函数，但无法刻画投资者行为。如同新古典经济学一样，对行为的处理简化为刺激——反应机制，行为的基础消失了。代表性的投资者和代表性的金融产品所构成的完全竞争市场满足了新古典一般均衡的条件，其代价就是在竞争市场均衡时的SDF也从主观因子变成了事实上的一致的客观因子。这种分析的简化和新古典经济学一样，把不确定性转化为基于概率的风险估计，而忽略了投资者对不确定性的主观感受的差别
【理性预期】萨金特：“理性预期...因为假定每个人都以相同的方式/logic 考虑未来的可能性，
《美国大萧条》这本书非常值得一读，不仅是关于美国大萧条的分析，更体现了奥地利学派独特的分析视角，那就是演绎与先验（a priori），而不是简单的统计归纳。在投资中，归纳法有着非常重要的作用，但同时也有着非常明显的缺陷，黑天鹅往往从此而出。只有从不同的视角看问题，不仅运用归纳法，更用演绎的方法分析问题，才能更接近真理。
1. （序言：徐光宪先生）陈伯敏教授在新著中的一个重要理念是：只有建立针对具体研究对象的物理模型才能指明通向物质世界真理的方向，而不是普适的数学模型。
2. （前言：陈伯敏先生）对于初学者，笔者愿意传达前辈们的忠告：准备草稿纸，动笔演绎。只要是理论学科，都要反复学几遍才能得要领，不要指望听一遍就懂得个大概，不要在“自我感觉差”面前退缩，“不懂”意味着正在入门，更不要指望寓教于乐。不过在熬过长夜、豁然开朗之际，“乐”却会不期而至，那是晨曦中第一原理送来的神圣感。
3. “人们持久的希望之一就是，找到几条简单而普遍的规律，来解释具有所有表面上的复杂性和多样性的自然为什么会如此。” —— Steven Weinberg（1979 Nobel Prize）
4. 郝柏林院士：“计算物理学的目的不是计算，而是理解、语言和发现新的物理现象。”
5. 从牛顿以来的三百多年，至少是关于无生命物质世界的第一性原理的框架已经建立，这就是量子力学和统计力学。
6. 在运用第一性原理的时候，选用适当的模型才能执行计算。在这里必须强调：物理模型比数学模型重要得多，只有在暂时无法构筑物理模型的场合才不得已采用数学模型。
7. 计算化学的目的不是计算，而是理解、预言和发现新的化学现象及其物理本质。
8. 19世纪中叶Wilhem von Humboldt曾经指出：科学首先有它的自我目的，至于它的实用性，其重要意义也仅仅是第二位的。
9. 化学不应该被肢解。
我的感受：在看到这里的时候，回想了一下自己的化学知识，感觉除了电化学之外，似乎在无机、有机、分析、物化这几个方面都有欠缺，需要在后面好好的补补自己的知识。
10. 基本概念的回顾：体系、环境、体系的宏观状态和微观状态、广义坐标（广义位置）、自由度、动力学状态（力学状态）、广义动量、相空间、力学量（动力学量）、体系的宏观状态、涨落、时间平均值（与宏观测量之间的关系）、非平衡定态（稳态）、平衡态、广延量和强度量、外参量和内参量、物态方程（本构方程）、正则变量、相空间、
我的感受：这一段中所描写的基本概念大家不妨考考自己，看看真正掌握的有多少。
11. 如果体系的势能U是的体系粒子收到的力
12. 模拟化学体系时，只要是在做看得到原子层次的模拟（所谓原子模拟，atomistic simulation），那么体系中不可能存在摩擦力，当又无外磁场存在，则总是保守系。
13. 在介观模拟（尺度为
14. Lagrange方程的有点在于它是关于独立变量之间的方程组，而Newton方程通常不是独立变量之间的方程组。从最小作用量原理得到Lagrange方程，而不是从Newton定律得到Lagrange方程，使得我们从单纯唯象的做法而进入力学的理性深处。
思考题：1. 什么是最小作用量原理？ 2. 如何从最小作用量原理得到Lagrange方程？（要注意吴大猷和Goldstein的变分方法的不同） 3. 如何从Lagrange方程看出Lagrange量的性质？ 4. 什么是Legendre变换？ 5. 如何利用Legendre变换从Lagrange量变成Hamilton量，进而推出Hamilton方程？ 6. 什么是m次Euler齐次函数？它有什么性质？ 7. 利用6的性质证明：在保守系的情况下，H就是体系总的机械能。对于能量守恒的体系，Hamilton函数就是体系总能量E。8. 利用最小作用原理和Hamiltonian给出Hamilton方程。 9. 推导Hamilton-Jacobi方程。 10. （没啥基本答案）说说Hamilton-Jacobi方程的意义，以及有何可以拓展的应用？
所需要的数学方法：（1）变分法，记得
看完第一章，大体的感觉就是：经典力学书籍的一个大概汇总，讲了最小作用原理以及Lagrangian和Hamiltonian，然后根据最小作用原理加上变分法推出来了Lagrange方程以及Hamilton方程。其实主要的目的是想让读者了解一下理论物理是如何处理问题的。从基本原理加上数学推演最后得到结论。那么化学中又是如何做的呢？第二章《势能面》会有描述。
CH2开个头：
15. “我们不说那些由基本原理推（导）不出来的话。” —— 录自喀兴林教授的《高等量子力学》，高等教育出版社1999年版，第80页
16. 本章从介绍Hohenberg-Kohn第一定理开始，在严格的量子理论的基础上建立“结构决定一切”的思想。明确了处于基态的化学体系，只要知道它们的核骨架（及分子结构），原则上就能以此为起点着手计算该体系的所有化学性质。核骨架就是位形空间中的位型，由此引出势能超曲面的概念，简称势能面。分析势能面的几何特点，尤其是其中的极小点（构象）和过渡态。
17. CH2还会介绍几种能量优化的方法：单纯形法、最速下降法、共轭梯度法、Newton-Raphson法以及寻找过渡态的几种方法。
To be continued...... 因为CH1后面都是公式推导，而我使用Latex也不是很熟练，因此先记录到这里，等有想法了再补充上去。欢迎大家及时关注！会持续更新。
http://blog.sciencenet.cn/blog-376446-757898.html 此文来自科学网何政达博客，转载请注明出处。
上一篇：【原创】电化学热力学
下一篇：【学习笔记】《计算化学-从理论化学到分子模拟》- 2 （23页~）
复旦固体物理讲义-14专题二：单电子近似(12.1)-五星文库
wxphp.com/wxd_14wom9boav3qhtz4wk5i_2.html
轉為繁體網頁
单电子，?Hartree-Fock近似，*单电子在所有电子的平均势场作用下运动——包含了Pauli不相容原理——考虑了交，*. 复旦固体物理讲义-14专题二：单电子近似(12.1).blog.sciencenet.cn/blog-376446-758013.html
内坐标法是通过价键的连接关系和键长r、键角
[PDF]球面上的測地線和一個平面幾何的問題
w3.math.sinica.edu.tw/math_media/d232/23203.pdf
球面上的測地線和一個平面幾何的問題. 張海潮. 一八五四年, 年僅二十八歲的黎曼, 在. 七十七歲的高斯面前就職演講「論幾何學之. 基礎假說」。 在這篇演講中, 他解釋 ...張量：測度與測地線
boson4.phys.tku.edu.tw/.../unit-07_Tensor__metric_n_geodesics.html
張量：測度與測地線. 線段元素與測度張量. 如何定(小線段) 長度？ 磐古開天（大霹靂、宇宙膨脹），如何想像？ （不是至大無外，至小無內嗎？所有東西的全體既稱為 ...http://www.weibo.com/james5664?from=feed&loc=at&nick=James5664
James5664
平权博弈的盎格鲁撒克逊商业社会不是理想乌托邦，但却是迄今为止(相对西亚绿教东亚红教南欧天主教东欧正教等级社会们而言)最合理的社会了。平权博弈在当代美国也是西海岸比东海岸更公平一些下层机会更多一些，西东海岸比中部内地更公平一些下层机会更多一些。
2013年出版的《中国经济下一步》第四章粗略提了方案。第一条，重订社会契约，其实是核心。
在卢卡斯等人的早期模型中，投资者的同质假定导致了CCAPM模型尽管引入了效用函数，但无法刻画投资者行为。如同新古典经济学一样，对行为的处理简化为刺激——反应机制，行为的基础消失了。代表性的投资者和代表性的金融产品所构成的完全竞争市场满足了新古典一般均衡的条件，其代价就是在竞争市场均衡时的SDF也从主观因子变成了事实上的一致的客观因子。这种分析的简化和新古典经济学一样，把不确定性转化为基于概率的风险估计，而忽略了投资者对不确定性的主观感受的差别
【理性预期】萨金特：“理性预期...因为假定每个人都以相同的方式/logic 考虑未来的可能性，
《美国大萧条》这本书非常值得一读，不仅是关于美国大萧条的分析，更体现了奥地利学派独特的分析视角，那就是演绎与先验（a priori），而不是简单的统计归纳。在投资中，归纳法有着非常重要的作用，但同时也有着非常明显的缺陷，黑天鹅往往从此而出。只有从不同的视角看问题，不仅运用归纳法，更用演绎的方法分析问题，才能更接近真理。
“Note that I make no pretense of using the historical facts to “test” the truth of the theory. On the contrary, I contend that economic theories cannot be “tested” by historical or statistical fact. These historical facts are complex and cannot, like the controlled and isolable physical facts of the scientific laboratory, be used to test theory. There are always many causal factors impinging on each other to form historical facts. Only causal theories a priori to these facts can be used to isolate and identify the causal strands.”
“Suffice it to say here that statistics can prove nothing because they reflect the operation of numerous causal forces.”
“Statistics can only record past events; they cannot describe possible but unrealized events.”
@刘海影
@刘海影
【泡沫】今天在一次私募高峰会上，关于目前股市是否有泡沫的问题上，与一位私募名家争论。他觉得没有，我觉得有。另一位嘉宾评论为屁股决定脑袋，我们做对冲自然谨慎，别人做long only自然希望长牛永不结束。也对。交易是观点的表达。无论如何，我觉得私募的价值在alpha，不在beta；beta是公募的领域。
即使存在不确定性，投资者所需做的仅仅是确定随机贴现因子（SDF）（Campbell，2000）。即尽管投资是面对未来的，金融产品的核心是平滑风险和收益，只要投资者能够估价金融产品未来的现金流，那么通过合理的SDF估计就能够准确计算这些产品的价格
行为资产定价理论综述1
陈彦斌 周业安
（中国人民大学经济学院 100872）
摘要：如何刻画投资者行为是资产定价理论50年来发展的主要脉络。在消费资本资产定价模型基础上，通过修正投资者的效用函数而发展起来的行为资产定价理论，对投资者行为的认识达到了新的高度。本文构造了行为资产定价的一般均衡研究框架，指出了此框架与行为金融理论的区别，并在此框架下综述了当前流行的行为资产定价模型。文章最后分析了行为资产定价理论的下一步发展方向。
关键词：行为资产定价理论；效用函数；消费资本资产定价模型
一、引言
在实际的市场活动中，理性的经济人面对着偏好、禀赋和时间等方面的不一致，需要寻求各种资源的最优配置，这种配置可以是空间上的，也可以是时间上的。只要每个人能够估计可能存在的各种机会的损益，并就这些估计达成共识（无论通过市场机制还是社会计划者），那么一般均衡实现时也就意味着每个人达到了最优配置状态。因此，一般均衡时市场的资源配置组合必然也是每个人所选择的最优配置组合。早期阿罗－德布鲁－麦肯齐一般均衡模型的思想被运用到金融学中。夏普等人假定，金融市场上每个人均是马克维茨所描述的均值—方差最优化者；每个人对资产的概率分布结构的看法一致，即对每项资产收益的均值，方差，以及协方差的估计都一致；任何人有且仅有一个借贷的无风险利率，而且无交易成本，在这种假定下，每人都购买同样的风险基金——市场组合（market portfolio）。这就是作为现代金融学奠基的资本资产定价模型（CAPM）的核心思想。
CAPM模型实际上就是阿罗－德布鲁－麦肯齐一般均衡模型的一个应用。和后者一样，CAPM模型不否认金融市场上的参与者可能面临的不确定性，但由于假定参与者是完全理性的，所以能够估计出可能发生的事件及其概率，并就此达成协议，结果不确定性转化为可计算的风险，参与者通过最优化均值——方差来寻求给定收益下的最小风险组合和给定风险下的最大收益组合。坎贝尔等人一再强调不确定性在资产定价研究中所起的关键作用（坎贝尔等，2003，第1页），不过这种不确定性的处理实际上背离了早期奥地利学派、凯恩斯及奈特等人所强调的不确定性和风险之差别的思想。在坎贝尔等人看来，只要市场上不存在套利机会（即金融市场是完全竞争的），即使存在不确定性，投资者所需做的仅仅是确定随机贴现因子（SDF）（Campbell，2000）。即尽管投资是面对未来的，金融产品的核心是平滑风险和收益，只要投资者能够估价金融产品未来的现金流，那么通过合理的SDF估计就能够准确计算这些产品的价格。在理论上，SDF和总消费的边际效用有关，即是现期边际效用和未来边际效用的折现率，是度量投资者跨期平滑的相对主观价格。在完全竞争的金融市场上，同质投资者对金融资产的主观估价和社会的估价一致，市场达到均衡。考虑到金融资产的未来现金流对同质的投资者来说是相同的，那么影响投资者决策差异的唯一变量就是SDF。
在夏普等人的早期模型中，投资者需要权衡的仅仅是金融资产的收益和风险，金融资产以外的因素很少被考虑。这种简化分析虽运用了一般均衡思想，严格来说还不是阿罗——德布鲁证券的均衡世界。直到Merton（1973）、Lucas（1978）、Breeden（1979）等提出了消费资本资产定价模型（CCAPM），使用资产收益率与总消费增长率的协方差描述风险，即消费贝塔。通过这种处理，CCAPM不仅引入了投资者的效用函数，使用投资者的相对风险规避系数来刻画投资者行为，而且能够在资本资产定价模型中同时考虑消
1
本文是中国人民大学“十五”“211工程”《中国经济学的建设和发展》子项目“行为和实验经济学学科规划”子报告研究成果。
wk_ad_begin({pid : 21});wk_ad_after(21, function(){$('.ad-hidden').hide();}, function(){$('.ad-hidden').show();});
2
费和投资的决策，这就把产品市场、要素市场和金融市场上的各种变量通过消费和投资的关系联系起来，由此真正获得对资产组合决策的一般均衡分析。CCAPM模型的提出是金融学的一次重大飞跃，将金融学的研究建立在一般均衡基础上，具有巨大的理论价值，在现代资产定价理论中有着巨大的影响。但是CCAPM无法解释股票溢价之谜（Mehra和Prescott，1985）和无风险利率之谜（Weil，1989）所展示的所谓金融市场“异常”现象，说明CCAPM模型有严重理论缺陷。
如前所述，对同质的投资者来说，决定其投资决策差异的唯一变量就是SDF，资产定价理论就是要通过模型精确刻画SDF的决定，引入不同的SDF决定因素，产生了相应的具体的资产定价模型（Campbell，2000）。在卢卡斯等人的早期模型中，投资者的同质假定导致了CCAPM模型尽管引入了效用函数，但无法刻画投资者行为。如同新古典经济学一样，对行为的处理简化为刺激——反应机制，行为的基础消失了。代表性的投资者和代表性的金融产品所构成的完全竞争市场满足了新古典一般均衡的条件，其代价就是在竞争市场均衡时的SDF也从主观因子变成了事实上的一致的客观因子。这种分析的简化和新古典经济学一样，把不确定性转化为基于概率的风险估计，而忽略了投资者对不确定性的主观感受的差别。正因如此，CCAPM模型才无法解释股权溢价之谜、股市波动之谜等金融市场“异常”。如坎贝尔指出的，新的资产定价理论就是寻找SDF的决定因子，寻找的方向就是引入各种异质假定，比如投资者偏好异质、收入异质、类型异质等（Campbell，2000）。
在资产定价理论中，异质假定的引入体现在对投资者效用函数的修正上，由此发展起来的资产定价理论获得了巨大的发展，这些理论模型已经逐步脱离原有模型对投资者行为的简化处理，开始考虑SDF行为层面的决定，以有效解释这些实证难题。从这个角度看，这些资产定价理论可称为“行为资产定价理论”
2
。总体上看，行为资产定价理论认为股票溢价之谜等实证难题来源于使用错误的效用函数来刻画投资者的
行为，从而在此效用函数基础之上构造出来的消费—投资组合模型不能正确地反映投资者的最优行为，最终导致错误地度量投资者的相对风险规避系数。也就是说，过去的理论没有真正理解现实的投资者行为，如果能够把效用函数的构造建立在对决策者心理活动规律的把握上，那么就能够恢复投资者的真实的效用函数，这些实证难题也就迎刃而解。通过吸收卡尼曼等人发展的行为经济学的一些基本原理，行为资产定价理论重新模型化投资者的决策行为，并把这些真实的决策行为嵌入到过去的资本资产定价模型中，获得了巨大的成功。比如，引入投资者的消费习惯因素，不仅能够解决投资者消费和投资的一般均衡问题，而且也能够有效解决投资者的跨期决策问题。行为资产定价理论通过对投资者行为的重新思考和模型化，逐渐替代过去的资本资产定价模型，成为现代金融理论解释金融市场活动的新基石。
行为资产定价理论的研究角度多种多样。一种代表性的角度是从CCAPM模型出发，逐步引入各种行为因素，比如财富偏好、习惯形成、追赶时髦、损失厌恶、嫉妒等，以此来实现更为精确的SDF刻画。大部分行为资产定价模型都是遵循这一研究方向。另一种研究方式是典型的行为金融学的理论的运用，它们直接从投资者行为的心理基础出发，研究投资者心理对资产价格的决定，进而影响金融市场的均衡，比如通过构造投资者的心理账户，来理解投资者对无风险资产和风险资产的组合投资及其定价，就是典型的一种模型方法。这方面的研究由于融入一般均衡框架的困难，使得比较少的人才产生兴趣。两种研究角度的关键差别在于前者一般假定投资者理性预期，而后者一般假定投资者有限理性，或者非理性。不过，通过许多金融学家的努力，两者已经开始逐渐相互融合。
2
国内很多人把行为经济学等同于心理学的经济学，强调当事人的非理性，这实际上是文献掌握过少所产生的误解。行为经济学在早期阶段的研究的确具有浓厚的心理学色彩，比如Kahneman、Thaler、Shiller、Shefrin、Statman等人的研究即是如此。但是，上世纪80年代开始，行为经济学家越来越注意对西蒙有限理性学说的继承，逐步通过有限理性建模来实现和主流经济学的融合，从目前看，这种融合取得了一定的成功。比如史莱佛、拉宾先后获得克拉克奖，卡尼曼、史密斯和阿克洛夫先后获得诺奖就足以说明这一点。新的行为经济学主要集中两个方面的研究——理性限制下行为的后果和偏好内生。本文对行为资产定价的定义遵从西蒙、史密斯、阿克洛夫、史莱佛、拉宾（Rabin）、卡梅瑞（Camerer）等人的行为经济学思想。这些学者认为，行为经济学的分析坚持理性这一出发点，但强调理性的限制，如拉宾所言，行为经济学不过是对主流经济学的修正而已（Rabin, 2002）。从这个角度讲，Shefrin和Statman等人对资产定价的研究在行为经济学中正在被边缘化，或者说至少目前没有追随者，本文关注的是主流经济学中行为资产定价理论的发展。
3
行为资产定价理论，按所采用的均衡框架划分，可以为局部均衡模型和一般均衡模型。在一般均衡模型中，不但投资者效用最大化，而且各个市场都必须达到均衡（商品市场出清和各个资产市场出清）。因此，在一般均衡模型中，投资者的最优决策行为，不但决定了他的消费水平和资产持有的投资组合，而且决定了各个资产的价格。也就是说，在一般均衡模型中，资产的价格（或者收益率）是内生的。而在局部均衡模型中，资产的价格是外生的，投资者将各个资产的价格视为给定的，并依此在效用最大化的过程中决定自己的最优投资组合。由于行为资产定价理论模型众多，即使讨论同一个效用函数，所采用模型基础也不尽相同。因此本文建立行为资产定价模型的一般均衡研究框架，然后在此框架基础之上，统一分析和综述各个行为资产定价模型。
虽然在本质上，研究资产定价理论并不一定需要一般均衡模型，但是出于如下考虑，本文统一采用一般均衡模型来综述行为资产定价理论。第一，大部分行为资产定价文献，特别是离散时间模型，都采用一般均衡模型。第二，局部均衡模型是一般均衡模型的退化情形，在一般均衡模型中，如果放松市场出清的要求，就得到了局部均衡模型。第三，局部均衡模型很难处理带有红利的定价理论，而一般均衡理论却可以十分便利地将股票的价格表示为其红利的价格。第四，一般均衡模型的计算方法和技巧更加丰富3。
本文的结构如下。第二节构造了行为资产定价模型的一般均衡研究框架。第三节介绍了主要的几个行为资产定价模型。第四节是结论和展望。
二、行为资产定价一般均衡框架
本节建立行为资产定价模型的一般均衡框架。考虑一个代表性投资者禀赋经济，经济类似于Lucas（1978），Mehra和Prescott（1985）和Bakshi和Chen（1996b）所研究的经济。
1 经济
考虑一个代表性投资者禀赋经济，代表性的投资者的t时财富为tW，希望使用该财富最大化期望终身总效用
0max(,)j
tjtjtjEucz，
此处tE是条件期望算子，是主观贴现因子，tc是消费。(,)ttucz表示修正后的效用函数，tz是进入效用函数的变量，随着所研究的行为资产定价模型的不同而不同，比如习惯、财富、损失等等。假定效用函数二次连续可微。
经济中有2n种公开交易的资产：Lucas树（股票），债券和n种金融资产。经济中的每一个投资者在初始时刻，都被赋予一棵树，称为Lucas树。如果将Lucas树理解为股票，那么Lucas树的果实则可以理解为股票的红利。每棵Lucas树的价格为tP，红利为ty。经济中的无风险资产是债券，相应的一期无风险利率记为btR。经济中还存在n种金融风险资产，假定每份风险资产i的从t时到1t时的收益率为1,tiR。
设代表性投资者在t期初持有ts棵Lucas树，价值为bttRL/的债券，数量为itN的风险资产i。那么投资者的t时财富在消费和各个资产之间分配，即
itnibt
t
ttttNRLsPcW1
投资者在1t时的财富等于各个资产的到期价值之和，即
1,1111)(tiitn
itttttRNLsyPW
3
Mehra和Presott（1985）和Abel（1990）等在一般均衡模型中，采用马氏链的方法计算股票和债券的期望收益率，并且这
一方法可以推广到所有行为资产定价中去；而HJ界等局部均衡方法则具有局限性，许多行为资产定价模型无法计算。
4
2 均衡
由于经济中的投资者是同质的，所以容易得到经济中的竞争性均衡。竞争性均衡是值函数(,)ttVWz、Lucas树的价格tP和需求数量ts，以及无风险利率btR，一方面使得投资者效用最大化，即值函数满足如下Bellman方程
11,,(,)max(,)(,)ttit
tttttttLsNVWzuczEVWz
另一方面使得市场出清。
3 均衡定价方程
投资者的控制变量则是所持有的资产数量，状态变量是财富和tz。不同的行为资产定价模型的具体求解过程有所不同，但思路大同小异。一般都是使用预算约束方程将消费替换为状态变量和控制变量，将下一期的财富替换为控制变量，代入Bellman方程。然后对控制变量求取一阶条件，并对状态变量使用Benveniste-Scheinkman公式4，得到如下Euler方程5，
111()tttEMR (1) 此处记号1
tR表示各个资产的收益率，即11()/tttPyy、btR和1,tiR，1()tM称为随机贴现因子（stochastic discount factor，简称SDF）。不同的行为资产定价模型具有不同的随机贴现因子，并且投资者的主观参数向量1(,...,)K不同。
本节虽然是在一般均衡模型基础上提出了行为资产定价理论的基本分析框架，但这个分析框架和以前的模型相比，存在着重要差别，即行为资产定价理论并不否认金融市场参与者的理性，但和传统理论不同，行为资产定价模型给参与者的理性施加了限制。因此，行为资产定价理论可以看作是对传统资产定价理论的延伸，与传统的金融学是兼容的。
首先，行为资产定价理论不排斥理性假定。
早期的资本资产定价模型不仅假定参与者是理性的，而且这种理性是完全的，任何影响投资者行为的因素都可以通过一个统一的简单的未来现金流的贴现方式加以解决。因此，在传统的资本资产定价模型中，不需要考虑投资者的行为限制。但行为资产定价理论并不接受投资者仅仅权衡收益－风险的两分法决策，而是考虑一个现实的投资者的行为本质究竟如何？按照新的理论，投资者在决策时不仅要权衡收益－风险，而且要决策本身收到消费习惯、财富禀赋、对损益的态度等的影响。也就是说，在行为资产定价理论中，参与者的理性受到限制了。这正是西蒙等人所倡导的有限理性的思想。
行为资产定价理论把参与者的限制从单纯的预算约束扩展到效用函数本身所包含的行为约束，这就使得金融学的研究更贴近投资者的真实状态。但和行为金融学中其它理论不同，行为资产定价理论更倾向于承认投资者的受限制的理性，而不是非理性。尽管希勒等人基于投资者非理性的研究对整个金融学理论构成了巨大的挑战。如此看来，行为资产定价理论更接近行为金融学中史莱佛、拉宾等人的研究，前者基于有限套利解释金融市场无效的来源；后者通过自我控制等理性限制来讨论参与者的跨期决策问题。但这些学者的研究始终强调参与人的理性本质，这一点和行为资产定价理论内在一致。
其次，行为资产定价与传统金融学是兼容的。
行为资产定价模型主要采用如下三类定价模型框架：消费－投资组合模型（consumption－portfolio choice mode）、资本资产定价模型和SDF模型。消费－投资组合模型，将投资者的最优消费和最优投资数
4 关于Benveniste-Scheinkman公式, 参见Ljungqvist和Sargent（2001）第31页。
5
投资者的规划问题的最优解除了满足Euler方程外，还必须满足横截性条件。
5
量，表示为其状态变量的函数。资本资产定价模型以及其扩展模型，如CCAPM，给出了资产的风险和收益之间的均衡线性关系。而SDF模型注重于分析资产的价格与回报之间的均衡关系6。
可以证明，上述三类定价框架，是等价的（Cochrane，2000）。比如说，用资产i的SDF模型，减去债券的SDF模型，适当变形，可以得到如资本资产定价模型的定价形式
)
()
,(cov][11,11,
tttittbttitMERMRRE
方程左边给出了资产的超额期望收益率，右边使用资产收益率与SDF的条件协方差来描述资产的风险。
由于所有行为资产定价模型均可表示为SDF模型的形式，而在经典金融学模型的等价性关系的证明过程中，只需要使用Riesz表示定理确保SDF的存在性与唯一性，并不需要SDF的具体表达式，所以行为资产定价理论与传统金融学是兼容的。那么行为资产定价理论与传统的金融学在本质上是一致，并不会破坏整个金融学理论的脉络和发展。最后，如果所有行为资产定价模型都表示为SDF形式，那么行为资产定价理论本身可以统一起来，具有一致的形式，这也方便以后对投资者行为的进一步研究和挖掘，以及在此基础上的行为资产理论的进一步发展。
运用行为资产定价理论的分析框架就能够有效解释金融市场上的各种“异常”。Mehra和Presott（1985）发表了著名的股票溢价之谜（Equity premium puzzle）。他们指出美国S&P500指数从1889年到1978年的平均年收益率约为7个百分点，而90天国库券从1931年到1978年的平均年收益率约为1个百分点。因此，如果投资者愿意购买如此低收益的债券，说明投资者是非常害怕风险的。经计算投资者的相对风险规避系数约为27。但是，一般认为投资者的相对风险规避系数小于2。对相对风险规避系数的如此之大的计算误差，这与现实相违背的。Weil（1989）指出无风险利率之谜（Riskless interest rate puzzle）：如果相对风险规避系数太大，就会导致无风险利率远远超过1个百分点。
下面使用SDF模型来陈述股票溢价之谜和无风险利率之谜。将经济学和金融学中最常用的CRRA型效用函数1()/(1)ucc
，代入SDF模型程，得到
1,10ttstbttcERRc和1
1ttbttcERc
， (2)
其中,1stR＝11()/tttPyy，第一个方程称为溢价方程，第二个方程称为无风险利率方程。
将美国的历史数据（消费增长率，S&P500指数收益率和短期债券收益率），代入溢价方程（2），可以计算出7参数约等于27。而一般认为，普通投资者的相对风险规避系数应该小于3。由于过高的风险溢价，而得到过高的相对风险规避系数，就是股票溢价之谜。
而将过高的相对风险规避系数代入无风险利率方程，用来计算债券的无风险利率，得到的无风险利率远远大于实际的平均水平（1%），这就是Weil（1989）的无风险利率之谜。
事实上，将股票溢价之谜和无风险利率之谜合并在一起，就是说不可能找到同时满足溢价方程和无风险利率方程的参数。
三、行为资产定价模型的具体讨论
虽然行为资产定价理论比传统资产定价理论更加贴近实际，但是也要接受实证的检验。而检验资产定价模型的基本方法是，检验所提出的资产定价模型能否解释股票溢价之谜和无风险利率之谜。如果不能够
6
如果用xt+1/ pt表示该资产的收益率，那么SDF模型也可以记为pt = Et(Mt+1xt+1)，即将任意一种资产当前价格，表示为资产
回报与SDF的乘积的条件期望。 7
计算方法可以参见Ljungqvist和SargentSargent（2000）第263页
即使存在不确定性，投资者所需做的仅仅是确定随机贴现因子（SDF）（Campbell，2000）。即尽管投资是面对未来的，金融产品的核心是平滑风险和收益，只要投资者能够估价金融产品未来的现金流，那么通过合理的SDF估计就能够准确计算这些产品的价格
如前所述，对同质的投资者来说，决定其投资决策差异的唯一变量就是
市场出清: clearing out 不确定性, subjective 效用, etc; = a process of
市场出清: clearing out 不确定性, subjective 效用, etc; = a process of
复旦固体物理讲义-14专题二：单电子近似(12.1)_百度文库
wenku.baidu.com/view/1d1f76eef8c75fbfc77db206
轉為繁體網頁
2010年6月1日 - 本讲目的? 从这一讲开始，我们进入固体物理学最核心的内容?能带理论。本讲介绍它的三个基本近似中的两个：绝热近似和单电子近似* 单电子近似 ...轉為繁體網頁
行为资产定价理论综述1
陈彦斌 周业安
（中国人民大学经济学院 100872）
摘要：如何刻画投资者行为是资产定价理论50年来发展的主要脉络。在消费资本资产定价模型基础上，通过修正投资者的效用函数而发展起来的行为资产定价理论，对投资者行为的认识达到了新的高度。本文构造了行为资产定价的一般均衡研究框架，指出了此框架与行为金融理论的区别，并在此框架下综述了当前流行的行为资产定价模型。文章最后分析了行为资产定价理论的下一步发展方向。
关键词：行为资产定价理论；效用函数；消费资本资产定价模型
一、引言
在实际的市场活动中，理性的经济人面对着偏好、禀赋和时间等方面的不一致，需要寻求各种资源的最优配置，这种配置可以是空间上的，也可以是时间上的。只要每个人能够估计可能存在的各种机会的损益，并就这些估计达成共识（无论通过市场机制还是社会计划者），那么一般均衡实现时也就意味着每个人达到了最优配置状态。因此，一般均衡时市场的资源配置组合必然也是每个人所选择的最优配置组合。早期阿罗－德布鲁－麦肯齐一般均衡模型的思想被运用到金融学中。夏普等人假定，金融市场上每个人均是马克维茨所描述的均值—方差最优化者；每个人对资产的概率分布结构的看法一致，即对每项资产收益的均值，方差，以及协方差的估计都一致；任何人有且仅有一个借贷的无风险利率，而且无交易成本，在这种假定下，每人都购买同样的风险基金——市场组合（market portfolio）。这就是作为现代金融学奠基的资本资产定价模型（CAPM）的核心思想。
CAPM模型实际上就是阿罗－德布鲁－麦肯齐一般均衡模型的一个应用。和后者一样，CAPM模型不否认金融市场上的参与者可能面临的不确定性，但由于假定参与者是完全理性的，所以能够估计出可能发生的事件及其概率，并就此达成协议，结果不确定性转化为可计算的风险，参与者通过最优化均值——方差来寻求给定收益下的最小风险组合和给定风险下的最大收益组合。坎贝尔等人一再强调不确定性在资产定价研究中所起的关键作用（坎贝尔等，2003，第1页），不过这种不确定性的处理实际上背离了早期奥地利学派、凯恩斯及奈特等人所强调的不确定性和风险之差别的思想。在坎贝尔等人看来，只要市场上不存在套利机会（即金融市场是完全竞争的），即使存在不确定性，投资者所需做的仅仅是确定随机贴现因子（SDF）（Campbell，2000）。即尽管投资是面对未来的，金融产品的核心是平滑风险和收益，只要投资者能够估价金融产品未来的现金流，那么通过合理的SDF估计就能够准确计算这些产品的价格。在理论上，SDF和总消费的边际效用有关，即是现期边际效用和未来边际效用的折现率，是度量投资者跨期平滑的相对主观价格。在完全竞争的金融市场上，同质投资者对金融资产的主观估价和社会的估价一致，市场达到均衡。考虑到金融资产的未来现金流对同质的投资者来说是相同的，那么影响投资者决策差异的唯一变量就是SDF。
在夏普等人的早期模型中，投资者需要权衡的仅仅是金融资产的收益和风险，金融资产以外的因素很少被考虑。这种简化分析虽运用了一般均衡思想，严格来说还不是阿罗——德布鲁证券的均衡世界。直到Merton（1973）、Lucas（1978）、Breeden（1979）等提出了消费资本资产定价模型（CCAPM），使用资产收益率与总消费增长率的协方差描述风险，即消费贝塔。通过这种处理，CCAPM不仅引入了投资者的效用函数，使用投资者的相对风险规避系数来刻画投资者行为，而且能够在资本资产定价模型中同时考虑消
1
本文是中国人民大学“十五”“211工程”《中国经济学的建设和发展》子项目“行为和实验经济学学科规划”子报告研究成果。
wk_ad_begin({pid : 21});wk_ad_after(21, function(){$('.ad-hidden').hide();}, function(){$('.ad-hidden').show();});
2
费和投资的决策，这就把产品市场、要素市场和金融市场上的各种变量通过消费和投资的关系联系起来，由此真正获得对资产组合决策的一般均衡分析。CCAPM模型的提出是金融学的一次重大飞跃，将金融学的研究建立在一般均衡基础上，具有巨大的理论价值，在现代资产定价理论中有着巨大的影响。但是CCAPM无法解释股票溢价之谜（Mehra和Prescott，1985）和无风险利率之谜（Weil，1989）所展示的所谓金融市场“异常”现象，说明CCAPM模型有严重理论缺陷。
如前所述，对同质的投资者来说，决定其投资决策差异的唯一变量就是SDF，资产定价理论就是要通过模型精确刻画SDF的决定，引入不同的SDF决定因素，产生了相应的具体的资产定价模型（Campbell，2000）。在卢卡斯等人的早期模型中，投资者的同质假定导致了CCAPM模型尽管引入了效用函数，但无法刻画投资者行为。如同新古典经济学一样，对行为的处理简化为刺激——反应机制，行为的基础消失了。代表性的投资者和代表性的金融产品所构成的完全竞争市场满足了新古典一般均衡的条件，其代价就是在竞争市场均衡时的SDF也从主观因子变成了事实上的一致的客观因子。这种分析的简化和新古典经济学一样，把不确定性转化为基于概率的风险估计，而忽略了投资者对不确定性的主观感受的差别。正因如此，CCAPM模型才无法解释股权溢价之谜、股市波动之谜等金融市场“异常”。如坎贝尔指出的，新的资产定价理论就是寻找SDF的决定因子，寻找的方向就是引入各种异质假定，比如投资者偏好异质、收入异质、类型异质等（Campbell，2000）。
在资产定价理论中，异质假定的引入体现在对投资者效用函数的修正上，由此发展起来的资产定价理论获得了巨大的发展，这些理论模型已经逐步脱离原有模型对投资者行为的简化处理，开始考虑SDF行为层面的决定，以有效解释这些实证难题。从这个角度看，这些资产定价理论可称为“行为资产定价理论”
2
。总体上看，行为资产定价理论认为股票溢价之谜等实证难题来源于使用错误的效用函数来刻画投资者的
行为，从而在此效用函数基础之上构造出来的消费—投资组合模型不能正确地反映投资者的最优行为，最终导致错误地度量投资者的相对风险规避系数。也就是说，过去的理论没有真正理解现实的投资者行为，如果能够把效用函数的构造建立在对决策者心理活动规律的把握上，那么就能够恢复投资者的真实的效用函数，这些实证难题也就迎刃而解。通过吸收卡尼曼等人发展的行为经济学的一些基本原理，行为资产定价理论重新模型化投资者的决策行为，并把这些真实的决策行为嵌入到过去的资本资产定价模型中，获得了巨大的成功。比如，引入投资者的消费习惯因素，不仅能够解决投资者消费和投资的一般均衡问题，而且也能够有效解决投资者的跨期决策问题。行为资产定价理论通过对投资者行为的重新思考和模型化，逐渐替代过去的资本资产定价模型，成为现代金融理论解释金融市场活动的新基石。
行为资产定价理论的研究角度多种多样。一种代表性的角度是从CCAPM模型出发，逐步引入各种行为因素，比如财富偏好、习惯形成、追赶时髦、损失厌恶、嫉妒等，以此来实现更为精确的SDF刻画。大部分行为资产定价模型都是遵循这一研究方向。另一种研究方式是典型的行为金融学的理论的运用，它们直接从投资者行为的心理基础出发，研究投资者心理对资产价格的决定，进而影响金融市场的均衡，比如通过构造投资者的心理账户，来理解投资者对无风险资产和风险资产的组合投资及其定价，就是典型的一种模型方法。这方面的研究由于融入一般均衡框架的困难，使得比较少的人才产生兴趣。两种研究角度的关键差别在于前者一般假定投资者理性预期，而后者一般假定投资者有限理性，或者非理性。不过，通过许多金融学家的努力，两者已经开始逐渐相互融合。
2
国内很多人把行为经济学等同于心理学的经济学，强调当事人的非理性，这实际上是文献掌握过少所产生的误解。行为经济学在早期阶段的研究的确具有浓厚的心理学色彩，比如Kahneman、Thaler、Shiller、Shefrin、Statman等人的研究即是如此。但是，上世纪80年代开始，行为经济学家越来越注意对西蒙有限理性学说的继承，逐步通过有限理性建模来实现和主流经济学的融合，从目前看，这种融合取得了一定的成功。比如史莱佛、拉宾先后获得克拉克奖，卡尼曼、史密斯和阿克洛夫先后获得诺奖就足以说明这一点。新的行为经济学主要集中两个方面的研究——理性限制下行为的后果和偏好内生。本文对行为资产定价的定义遵从西蒙、史密斯、阿克洛夫、史莱佛、拉宾（Rabin）、卡梅瑞（Camerer）等人的行为经济学思想。这些学者认为，行为经济学的分析坚持理性这一出发点，但强调理性的限制，如拉宾所言，行为经济学不过是对主流经济学的修正而已（Rabin, 2002）。从这个角度讲，Shefrin和Statman等人对资产定价的研究在行为经济学中正在被边缘化，或者说至少目前没有追随者，本文关注的是主流经济学中行为资产定价理论的发展。
3
行为资产定价理论，按所采用的均衡框架划分，可以为局部均衡模型和一般均衡模型。在一般均衡模型中，不但投资者效用最大化，而且各个市场都必须达到均衡（商品市场出清和各个资产市场出清）。因此，在一般均衡模型中，投资者的最优决策行为，不但决定了他的消费水平和资产持有的投资组合，而且决定了各个资产的价格。也就是说，在一般均衡模型中，资产的价格（或者收益率）是内生的。而在局部均衡模型中，资产的价格是外生的，投资者将各个资产的价格视为给定的，并依此在效用最大化的过程中决定自己的最优投资组合。由于行为资产定价理论模型众多，即使讨论同一个效用函数，所采用模型基础也不尽相同。因此本文建立行为资产定价模型的一般均衡研究框架，然后在此框架基础之上，统一分析和综述各个行为资产定价模型。
虽然在本质上，研究资产定价理论并不一定需要一般均衡模型，但是出于如下考虑，本文统一采用一般均衡模型来综述行为资产定价理论。第一，大部分行为资产定价文献，特别是离散时间模型，都采用一般均衡模型。第二，局部均衡模型是一般均衡模型的退化情形，在一般均衡模型中，如果放松市场出清的要求，就得到了局部均衡模型。第三，局部均衡模型很难处理带有红利的定价理论，而一般均衡理论却可以十分便利地将股票的价格表示为其红利的价格。第四，一般均衡模型的计算方法和技巧更加丰富3。
本文的结构如下。第二节构造了行为资产定价模型的一般均衡研究框架。第三节介绍了主要的几个行为资产定价模型。第四节是结论和展望。
二、行为资产定价一般均衡框架
本节建立行为资产定价模型的一般均衡框架。考虑一个代表性投资者禀赋经济，经济类似于Lucas（1978），Mehra和Prescott（1985）和Bakshi和Chen（1996b）所研究的经济。
1 经济
考虑一个代表性投资者禀赋经济，代表性的投资者的t时财富为tW，希望使用该财富最大化期望终身总效用
0max(,)j
tjtjtjEucz，
此处tE是条件期望算子，是主观贴现因子，tc是消费。(,)ttucz表示修正后的效用函数，tz是进入效用函数的变量，随着所研究的行为资产定价模型的不同而不同，比如习惯、财富、损失等等。假定效用函数二次连续可微。
经济中有2n种公开交易的资产：Lucas树（股票），债券和n种金融资产。经济中的每一个投资者在初始时刻，都被赋予一棵树，称为Lucas树。如果将Lucas树理解为股票，那么Lucas树的果实则可以理解为股票的红利。每棵Lucas树的价格为tP，红利为ty。经济中的无风险资产是债券，相应的一期无风险利率记为btR。经济中还存在n种金融风险资产，假定每份风险资产i的从t时到1t时的收益率为1,tiR。
设代表性投资者在t期初持有ts棵Lucas树，价值为bttRL/的债券，数量为itN的风险资产i。那么投资者的t时财富在消费和各个资产之间分配，即
itnibt
t
ttttNRLsPcW1
投资者在1t时的财富等于各个资产的到期价值之和，即
1,1111)(tiitn
itttttRNLsyPW
3
Mehra和Presott（1985）和Abel（1990）等在一般均衡模型中，采用马氏链的方法计算股票和债券的期望收益率，并且这
一方法可以推广到所有行为资产定价中去；而HJ界等局部均衡方法则具有局限性，许多行为资产定价模型无法计算。
4
2 均衡
由于经济中的投资者是同质的，所以容易得到经济中的竞争性均衡。竞争性均衡是值函数(,)ttVWz、Lucas树的价格tP和需求数量ts，以及无风险利率btR，一方面使得投资者效用最大化，即值函数满足如下Bellman方程
11,,(,)max(,)(,)ttit
tttttttLsNVWzuczEVWz
另一方面使得市场出清。
3 均衡定价方程
投资者的控制变量则是所持有的资产数量，状态变量是财富和tz。不同的行为资产定价模型的具体求解过程有所不同，但思路大同小异。一般都是使用预算约束方程将消费替换为状态变量和控制变量，将下一期的财富替换为控制变量，代入Bellman方程。然后对控制变量求取一阶条件，并对状态变量使用Benveniste-Scheinkman公式4，得到如下Euler方程5，
111()tttEMR (1) 此处记号1
tR表示各个资产的收益率，即11()/tttPyy、btR和1,tiR，1()tM称为随机贴现因子（stochastic discount factor，简称SDF）。不同的行为资产定价模型具有不同的随机贴现因子，并且投资者的主观参数向量1(,...,)K不同。
本节虽然是在一般均衡模型基础上提出了行为资产定价理论的基本分析框架，但这个分析框架和以前的模型相比，存在着重要差别，即行为资产定价理论并不否认金融市场参与者的理性，但和传统理论不同，行为资产定价模型给参与者的理性施加了限制。因此，行为资产定价理论可以看作是对传统资产定价理论的延伸，与传统的金融学是兼容的。
首先，行为资产定价理论不排斥理性假定。
早期的资本资产定价模型不仅假定参与者是理性的，而且这种理性是完全的，任何影响投资者行为的因素都可以通过一个统一的简单的未来现金流的贴现方式加以解决。因此，在传统的资本资产定价模型中，不需要考虑投资者的行为限制。但行为资产定价理论并不接受投资者仅仅权衡收益－风险的两分法决策，而是考虑一个现实的投资者的行为本质究竟如何？按照新的理论，投资者在决策时不仅要权衡收益－风险，而且要决策本身收到消费习惯、财富禀赋、对损益的态度等的影响。也就是说，在行为资产定价理论中，参与者的理性受到限制了。这正是西蒙等人所倡导的有限理性的思想。
行为资产定价理论把参与者的限制从单纯的预算约束扩展到效用函数本身所包含的行为约束，这就使得金融学的研究更贴近投资者的真实状态。但和行为金融学中其它理论不同，行为资产定价理论更倾向于承认投资者的受限制的理性，而不是非理性。尽管希勒等人基于投资者非理性的研究对整个金融学理论构成了巨大的挑战。如此看来，行为资产定价理论更接近行为金融学中史莱佛、拉宾等人的研究，前者基于有限套利解释金融市场无效的来源；后者通过自我控制等理性限制来讨论参与者的跨期决策问题。但这些学者的研究始终强调参与人的理性本质，这一点和行为资产定价理论内在一致。
其次，行为资产定价与传统金融学是兼容的。
行为资产定价模型主要采用如下三类定价模型框架：消费－投资组合模型（consumption－portfolio choice mode）、资本资产定价模型和SDF模型。消费－投资组合模型，将投资者的最优消费和最优投资数
4 关于Benveniste-Scheinkman公式, 参见Ljungqvist和Sargent（2001）第31页。
5
投资者的规划问题的最优解除了满足Euler方程外，还必须满足横截性条件。
5
量，表示为其状态变量的函数。资本资产定价模型以及其扩展模型，如CCAPM，给出了资产的风险和收益之间的均衡线性关系。而SDF模型注重于分析资产的价格与回报之间的均衡关系6。
可以证明，上述三类定价框架，是等价的（Cochrane，2000）。比如说，用资产i的SDF模型，减去债券的SDF模型，适当变形，可以得到如资本资产定价模型的定价形式
)
()
,(cov][11,11,
tttittbttitMERMRRE
方程左边给出了资产的超额期望收益率，右边使用资产收益率与SDF的条件协方差来描述资产的风险。
由于所有行为资产定价模型均可表示为SDF模型的形式，而在经典金融学模型的等价性关系的证明过程中，只需要使用Riesz表示定理确保SDF的存在性与唯一性，并不需要SDF的具体表达式，所以行为资产定价理论与传统金融学是兼容的。那么行为资产定价理论与传统的金融学在本质上是一致，并不会破坏整个金融学理论的脉络和发展。最后，如果所有行为资产定价模型都表示为SDF形式，那么行为资产定价理论本身可以统一起来，具有一致的形式，这也方便以后对投资者行为的进一步研究和挖掘，以及在此基础上的行为资产理论的进一步发展。
运用行为资产定价理论的分析框架就能够有效解释金融市场上的各种“异常”。Mehra和Presott（1985）发表了著名的股票溢价之谜（Equity premium puzzle）。他们指出美国S&P500指数从1889年到1978年的平均年收益率约为7个百分点，而90天国库券从1931年到1978年的平均年收益率约为1个百分点。因此，如果投资者愿意购买如此低收益的债券，说明投资者是非常害怕风险的。经计算投资者的相对风险规避系数约为27。但是，一般认为投资者的相对风险规避系数小于2。对相对风险规避系数的如此之大的计算误差，这与现实相违背的。Weil（1989）指出无风险利率之谜（Riskless interest rate puzzle）：如果相对风险规避系数太大，就会导致无风险利率远远超过1个百分点。
下面使用SDF模型来陈述股票溢价之谜和无风险利率之谜。将经济学和金融学中最常用的CRRA型效用函数1()/(1)ucc
，代入SDF模型程，得到
1,10ttstbttcERRc和1
1ttbttcERc
， (2)
其中,1stR＝11()/tttPyy，第一个方程称为溢价方程，第二个方程称为无风险利率方程。
将美国的历史数据（消费增长率，S&P500指数收益率和短期债券收益率），代入溢价方程（2），可以计算出7参数约等于27。而一般认为，普通投资者的相对风险规避系数应该小于3。由于过高的风险溢价，而得到过高的相对风险规避系数，就是股票溢价之谜。
而将过高的相对风险规避系数代入无风险利率方程，用来计算债券的无风险利率，得到的无风险利率远远大于实际的平均水平（1%），这就是Weil（1989）的无风险利率之谜。
事实上，将股票溢价之谜和无风险利率之谜合并在一起，就是说不可能找到同时满足溢价方程和无风险利率方程的参数。
三、行为资产定价模型的具体讨论
虽然行为资产定价理论比传统资产定价理论更加贴近实际，但是也要接受实证的检验。而检验资产定价模型的基本方法是，检验所提出的资产定价模型能否解释股票溢价之谜和无风险利率之谜。如果不能够
6
如果用xt+1/ pt表示该资产的收益率，那么SDF模型也可以记为pt = Et(Mt+1xt+1)，即将任意一种资产当前价格，表示为资产
回报与SDF的乘积的条件期望。 7
计算方法可以参见Ljungqvist和SargentSargent（2000）第263页
No comments:
Post a Comment