群速度相速度 相速度：是对个人来说的，队伍中每一个人的行进速度不同；就是说光脉冲中每个光频率(vi)的传播速度不同（因此每个光波的频率不相同），每个频率都有一个自己的相速度

相对速度，群速度相速度，快慢光，超光速，光孤子，飞秒阿秒

已有 3093 次阅读 2013-1-13 02:08 |个人分类:科普|系统分类:科普集锦|关键词:Microsoft 数学题 小学生 相对论 style

一不小心，一道小学生的数学题在科学网上引发一场众人关注的血案（小红花）

先是一篇鲍博主的《相对论---破解一道小学数学题 》，本来就是一个‘相对速度’的问题，被望文生意成爱因斯坦的‘相对论’，于是引来一批人围观，指指点点，岂不知，大多数人的指点都是错误的，因为思维上没有转弯，还不如队伍中的最后那位，跑到最前头就180度的急转弯。

然后来了一篇《补记》，的确，这个和这类问题不应该送给小学生去考虑，至少它用到了根号问题。合适的问题可以是一位博友说的，一位在行进的火车上跑前跑后的问题。

我开始注意到的时候，也就已经血流遍地了，就是程博主的《也谈“相对速度”》。

这个问题的原本就是那头无头的苍蝇来回飞的问题，地地道道的数学上的无穷级数问题：

程博主博文引用为：

(2) 关晴骁问题（见首篇[34]）

两辆自行车A，B间隔100米相向而行，两车都是每秒走一米，他们出发那一刻，一苍蝇每秒2米的速度从A车直线往B车飞，飞到B车后转头又往A车飞，问两车相遇时，苍蝇飞了多少米？ 

据说别人问哪个诺依曼来着，诺依曼立刻回答100米，然后那人很赞叹的说“我本还以为你会用无穷级数来算”，诺依曼说“我就是用那个算的”。。。好像出自《读者》？

这个无穷级数问题的超级简化，只取第一项，就是鲍博主提到的，继续引用如下，

鲍得海问题（见首篇[29]）：一列队伍长M米，向前行驶，队伍中最后一个人，以较快的速度沿着同样的方向前进，当这个人走到队伍的最前头的时候，返回身来再往回走，一直走到队伍的最后，这时，整列队伍恰好向前行走了N米。提问：单独的这个人走了多少距离？

最后演化成为难倒小学生，大学生到一帮博主的问题，

一列队伍长一百米，向前行驶，队伍中最后一个人（二者均为匀速），以较快的速度沿着同样的方向前进，当这个人走到队伍的最前头的时候，返回身来再往回走，一直走到队伍的最后，这时，整列队伍恰好向前行走了100米。提问：单独的这个人走了多少路程？

这些问题的答案上面三篇博文中已经交待得很清楚了。但是，我觉得血流还远远不够，还需要继续大刀阔斧地往下砍，骨头需要劈开，看清楚里面的骨髓脑髓，自道是那白的红的一道露出来了。

关键核心问题是，一列队伍长M米，向前行驶，如果队伍中每一个人，以不同的速度沿着同样的方向前进，结果会怎样？

找到一个非常贴切的例子是，物理学中光学学科的群速度，相速度和相关的超光速，慢光速问题。

对于这个行进中的队伍，就是一个光脉冲，其中包括了很多光的频率，怎样一起向前传播的问题。这里每一个光的频率是v_i，对应一个波长 λ_i。

相速度：是对个人来说的，队伍中每一个人的行进速度不同；就是说光脉冲中每个光频率(v_i)的传播速度不同（因此每个光波的频率不相同），每个频率都有一个自己的相速度。

群速度：就是整个队伍的行进速度，光脉冲中许多不同频率的光波合成在一起在介质中传播的整体速度。不同频率波的振幅和相位不同，在介质中，相速度因此不同，故在不同的空间位置上的合成信号形状会发生变化。群速度是一个代表整体能量的传播速度。

关键一点是，队伍中每个成员的体力和身体素质不同，导致相速度不同，行进中会产成队伍的次序重组现象，有的开始靠前，过一段时间/距离以后就变得靠后，反之亦然，开始时刻靠后的，后来会变得靠前，也有可能更靠后，这样队伍会被缩短，或者拉长，特殊情况也就是理想状况下，各个成员身体素质和体力相同，则队伍形状不变。

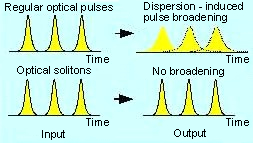
相对应，光脉冲向前传播中的过程完全类似，因为介质（真空除外）都有一定的折射率n，对每个光波长（λ_i，频率v_i)）不同，称为 n_i，导致不同光频率(v_i)的传播速度（相速度）也不同。所以，光脉冲会被介质拉长，这是最普遍情况，甚至缩短，这是极少情况，甚至在特定情况下相对速度不变，叫做光孤子。缩短情况也是相对而言的，因为缩到最短之后再继续向前传播就是拉长了，这就相当于，开始的队伍前头落到了最后头，体力跟不上了，把队伍拉长了，甚至最后掉队了。

这里顺便把快光速（也叫超光速）和慢光速问题也就说明了，这两个术语就是指的是光的相速度相对于群速度问题。还可以比喻说，一列队伍缓慢进行，有队员脚步跳得很快但是实际上没有向前跑很快，极端情况是原地踏步走。也有队伍行进快，但是队员迈步较慢但是步伐很大的情况（完全跟得上队伍），这就是慢光速了，极端的例子是光速为零，这个领域每隔几年 媒体就会热炒，外行吃惊，内行则不以为然。

现在的光速大概是每秒30万公里，托爱因斯坦他老人家引入的这个假设的福，这个极限我不相信在宇宙中我们所处的这一块领地能够被打破。至于2011年的意大利的中微子超光速一说，这里的超光速是指群速度而不是相速度，刚出现的时候真正内行人中大家的直觉就是乌龙，事后证明的确是，因为他们的那一套实验虽然复杂但是原理根本不靠谱。

回到光波的队伍传播话题上来。光纤通讯中这就有一个很现实很重要的关键问题：光脉冲在光纤中传播的时候不管拉长还是缩短，最终结果是拉长，都会造成失真，导致接受到的光脉冲信号和发出去的光脉冲信号混淆乃至分不清，从而达不到传输信号的作用。现在使用的妥协办法就是，让前后发出的光脉冲队伍间隔时间加长，这个就算每个光脉冲拉长了，到达终点的时候还能分得开，没有跟后面的队伍混淆一起。所以，现在的光纤通讯都要有中继站，一则补充传输中信号强度的损失，二者重新注入新的光脉冲，这相当于恢复光脉冲队伍的原有形状。比如，北京到广州的火车（或者上海到拉萨）虽有直达特快，但是中途仍然需要停靠以补充用水食品等，高铁通了，这样的折腾减少了，这就是高技术的进步。但是，北京到广州的光纤通讯，还需要很多中继站，好像是让光脉冲的火车停靠以加水加食品，实际上是换了光脉冲的火车而已，信息需要从一列光火车换乘到另一列。如果我们的光纤通讯技术能做到，光脉冲从北京进去直达广州再出来，中间不停靠不换光火车，那就是特别高的高技术了。 这就需要发展光纤通讯的高铁技术——光孤子通讯技术了。所谓的光孤子通信技术，就是发展出特定的光脉冲，在特定的光纤里面传播特别长一段距离，光脉冲的队伍依然很整齐（参见下图左）。这跟高铁跑在专用轨道上一个道理。这里是高技术，也包含了深刻了科学前沿领域。

  

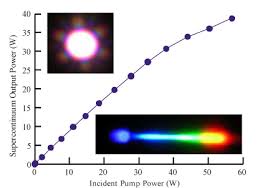
更深刻更科学前沿一点，就再多说一点点本博主的老本行，飞秒激光（femto-second laser）。飞秒激光就是一种非常短的光脉冲，这个光的队伍特别长，就是说对应的光波长（λ_i）很多，越多光波长加进去这个队伍，这个光脉冲时间就很有可能更短（量子测不准原理决定的）。现在同行都知道，把整个可见光都包括进去都已经很容易了，看起来就是白光，跟太阳光谱非常接近，也就是说，很容易展示出一个飞秒光脉冲，用牛顿的三角棱镜散开以后看到从深蓝到深红都有，技术上这一点都不麻烦（见上图右）。关键问题是，如果管理好这个光频率队伍前进中的整齐度问题，因为这个队伍太容易被拉长而变形得不像样，也就是说保持飞秒的传播很困难，顺便，光孤子通讯技术也在这个领域。顺便多说一句，日常照明的荧光灯的那个白光不是真正的白光，里面包含了太阳白光的几个很窄的波段，用以骗过人的眼睛而已。

那么，能不能包含更多更多的光波长（λ_i）进来，从而把这个光脉冲的时间变得比飞秒还短？答案是肯定的，absolutely true! 这个新术语就是阿秒（atto-second）。但是，可见光范围内的光波长（λ_i）还是太长，实现起来特别困难，人们就移到X-射线领域，那里频率非常高就是波长非常短，相对而言可以得到很长的光波队伍，才可能够容易地得到阿秒激光。这个领域是高技术最前沿，也是科学的一大前沿。目前，世界上只有一个课题组宣称得到了阿秒（某西方国家），很多人表示基本认可，但是需要其它课题组重复出来，也就是实验验证。整个世界的主要国家都在努力进行，第二个和后来的结果也许证明第一个结果是对的，那么前两家有可能得到诺奖！如果后来证明第一家的是错误的，那就还需要推倒重来，重新争做世界上第一个阿秒王/阿秒帝。anyway，这个领域需要诺奖，不言而喻！

不好意思，从一个小学生的简单数学问题，扯到了如此的科学和技术前沿，实质就是一个队伍向前行进中的队形问题。 

你也可以倒过来说，科学和高技术的前沿，其实也是小学生级别的问题，这样看，大家都是小学生了，难道不是吗？


Unformatted text preview: 纳并加以发展。 〈 角动量量子化条件 〉原子核外电子所具有的 J m = h 进一步揭示了核外电子呈分立定态存在的事实，丰富了量子化的内 容。但是 Bohr 利用经典轨道概念将量子化条件表达为动量对坐标的 回路积分的形式则是一种不成功的尝试，已被后来诞生的量子力学所 否定。 § 1.2 基本观念 1, 基本图像： de Broglie 关系与波粒二象性 1905 年 Einstein 通过提出下列关系 E h = = ν h ， k e h e c E p v h v v v = = = λ (1.9) （这里 π 2 h = h ），引入光子的概念。这在原先认为光是电磁波的图象 上添加了粒子的图象，这已由上节第一组实验所证实。于是，若知道 等式右边的波动参数 和 k ，便可用这组关系求得它左边的量所相应 的微粒子特性。 经过 18 年之久， de Broglie 克服积习的约束，逆过来 理解这组关系，将上面这组关系从针对 m = 的情况推广到 m ≠ 的情 况，提出原先是微粒的微观粒子也具有波动性 1 ， 1 Louis De Broglie , Waves and Quanta, Nature, Vol .112, 540 (1923) 。 9 ω = E h ， v v h k p = ， ( 1 . 1 ) 就是说，若已知等式右边的粒子参数 E 和 p v ，便可由这组关系式求得 该粒子所具有的波动特性。上面 两组关系式的中间桥梁便是 Planck 常数 h ， 形象地写出便是 ( , ) ( , ) E p k v v h ← → ⎯ 公式（ 1 。 10 ）便是常说的 de Broglie 关系 。 其中关于波长的第二个 公式已为上节第二组实验所证实，而关于频率的第一个公式则被原子 光谱实验所证实。 注意，这组 de Broglie 关系是物质世界的普遍规律。 其中将两种图象联系起来的 Planck 常数 h 数值很小，是波粒二象性可 以显现出来的标度。假如在所研究问题中能够认为 h → ，波和粒子 便截然分开，波粒二象性的现象便可以忽略。 比如，由原先粒子的 ( , ) E p v ，利用 (1.10) 第二式便得到 λ → ，与此粒子相联系的波动性便 可以忽略。于是可以说， 经典力学是量子力学当 h → 时的极限情况。 当然，这里 h → 是相对而言，并非真要 ( 本就是常数的 ) h 变小，而是 要求研究对象的动量 p 足够大 ( 从而波长 足够短 ) ，以及运动涉及的 空间尺度 l 足够大，使得 pl << h 即可。简单些说， 可以按 Planck 常数 h 在所研究的问题里能否忽略， 决定波粒二象性是否表现出来，进而决定经典与量子的界线。于是， 经典力学只不过是其研究对象的能量、动量以及运动的空间尺度如此 之大，使得 h 的作用可忽略情况下的力学。 综上所述，不论静止质量为零和不为零的微观物质，都普遍存在 波粒二象性。这两种截然不同的属性通过 Planck 常数连结成为 de Broglie 关系，统一在所有微观物质上。对初学者而言， 波粒二象性 是理解微观物质普遍属性的基本图象，也是初学者理解量子力学的基...