复色光才可能给细胞折腾吸收
波函数是概率波。其模的平方代表粒子在该处出现的概率密度。
既然是概率波，那么它当然具有归一性。即在全空间的积分。
然而大多数情况下由薛定谔方程求出的波函数并不归一。所以要在前面乘上一个系数N，即，然后把它带入归一化条件,解出N。至此，得到的才是归一化之后的波函数。注意N并不唯一。
波函数
波函数不是买彩票的中奖几率，彩票的中奖几率是线性相加的，买两张彩票，中奖几率就变为2倍，买N张彩票，中奖几率就是N倍。波函数具有相干性，具体地说，两个波函数叠加，概率并非变成12+12=24倍，而是在有的地方变成(1+1)2=4倍，有的地方变成(1-1)2=0，具体取决于两个波函数的相位差。联想一下光学中的杨氏双缝实验，不难理解这个问题
波函数29]nature2014
- [28]陈楷翰
- 尤其是，呃假如而已，假如和拉曼光谱结合的时候，把生物搞不舒服了，拉曼测出来的化学物质中间体的品种啊浓度啊啥的肯定变。。。。。。呃
- [27]陈楷翰
- 弱是弱，对于一个草履虫而言，一束强光过去它立马不自在。。。。。。呃真的
- [26]陈楷翰
- 对，有道理。只有这样才能解释荧光干涉消除，以及彩色的问题；而且途中真的可能还能实现光电倍增，由此降低入射光功率，规避热量与强光对生物体的危害，便于观察活生物的一些细节活动；嗯好玩，真的好玩！好玩！
- 博主回复(2014-10-8 20:48)：光毒作用很弱。
- [25]陈楷翰
- 可能有些明白了：多个波长的荧光照片叠加成像。
有趣，有趣！好玩！ - 博主回复(2014-10-8 20:42)：可以一次拍出来，每个接受器一个颜色，最后用计算机合成。
- [24]陈楷翰
-
哥们，不生气啊，我好奇的时候情商一直就是零的。。。。。。不是有意的。 - 博主回复(2014-10-8 20:35)：给你贴了一幅图片，欣赏下，慢慢体会。
- [23]陈楷翰
- 发出的荧光是有颜色的，通过给不同细胞的染色不同，就是彩色了。
——————————————————很不合理，激发荧光单色，可复色光才可能给细胞折腾吸收啊？ 给不同细胞染色？也不能被吸收啊？不吸收了咋显示出彩色？ - 博主回复(2014-10-8 20:33)：这个是光物理的基本原理：第二束光把荧光灭掉。
不在这个学科，记住就可以了，理解需要时间。
曲率的概念是為了度量空間的彎曲程度所產生的數學量，而在高維度的微分幾何學裡，曲率可以看成是度量向量場二次微分的交換程度(這與空間的彎曲程度有關係)。假設
是向量場，我們定義![R(X,Y)Z=D_{X}D_{Y}Z-D_{Y}D_{X}Z-D_{[X,Y]}Z.](https://s0.wp.com/latex.php?latex=R%28X%2CY%29Z%3DD_%7BX%7DD_%7BY%7DZ-D_%7BY%7DD_%7BX%7DZ-D_%7B%5BX%2CY%5D%7DZ.&bg=FFFFFF&fg=000000&s=0 "R(X,Y)Z=D_{X}D_{Y}Z-D_{Y}D_{X}Z-D_{[X,Y]}Z.")
是光滑向量場，我們很自然的可以得到曲率張量為零。然而在一般的黎曼流形中，空間的彎曲程度會影響著向量場的二次微分項。取局部座標
後，我們把黎曼曲率張量寫成局部座標的形式:
Ricc曲率張量
定義為
(1)first Bianchi:
(2)second Bianchi:
(3)
(換句話說
.)任給
上的向量場
。假設
是
形成的
的二維向量子空間，我們定義截面張量
利用局部座標系，我們還可以把
表示成
的形式:
Cartan的流形微分學
假設
是上的向量場。我們說
是直交的若且唯若
為上的一組活動標架(moving frame)。令
表示的對偶場。(換句話說，
)則我們知道
是2-form。定理:存在one-forms
滿足
使得
我們稱
為connection-one-forms.
為connection-one-forms.
證明:令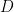
表示上的黎曼聯絡，且定義來自:
表示上的黎曼聯絡，且定義來自:
那麼利用黎曼聯絡的性質，我們可以得到此結果。
定義
則我們稱矩陣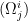
是curvature- 2-form。由於
在每個點
上都是
的基底，因此我們可以把
寫成的表示:
是curvature- 2-form。由於在每個點上都是的基底，因此我們可以把寫成的表示:
其中
為黎曼曲率張量。其中，
為黎曼曲率張量。其中，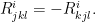
範例:假設
為黎曼曲面，則curvature 2-form為
為黎曼曲面，則curvature 2-form為
其中我們知道曲面的高斯曲率為
註記:所以大家應該可以看到，利用活動標價的方法(Cartan的微分學)可以簡化很多流形上張量的計算。應用的話，大家可以閱讀:曲面的高斯曲率的計算。
2014化学诺奖：超分辩光学显微镜是物理仪器 《微分几何入门与广义相对论（上册·第二版）》的笔记-第三章 黎曼内稟曲率张量
- 章节名：第三章 黎曼内稟曲率张量
- 2014-09-11 20:43:25
本章内容大致与作者老师所作 http://book.douban.com/subject/1768648/ 第三章相同 适合交叉阅读- 几何学的目的是研究单参变换群下的不变量 此过程开发出来的几何语言常用于描述物理世界在欧氏几何中这些不变量通常由 点 矢量 距离 夹角等概念描述欧氏空间是平直的 矢量沿任何轨迹的平移都不会影响夹角 两条平行线永远也不会相交 但经验发现 欧式几何不足以描述物理世界的规律-在微分几何中 空间不再假设为平直的 每一点上都有局部特殊的矢量空间 这些矢量被定义为该点上的泛函 微积分中的导数算子也被推广到这些矢量及相应的张量上 且可以写作偏微分算子与克氏符的形式在某曲线上的平移由以下包含导数算子的微分方程定义 其中 为曲线的切矢
精选
|||
昨天蓝光诺奖参合太多了，化学就不想参合了，谁知道，全慧又及时转来消息：
这下麻烦了，更加落到我的领域范围之内了，不得不说点。
[13]刘全慧
2014 Nobel Prize in Chemistry
The Nobel Prize in Chemistry 2014 was awarded jointly to Eric Betzig, Stefan W. Hell and William E. Moerner "for the development of super-resolved fluorescence microscopy".
获奖原因：他们开发了超分辨荧光显微镜。
去年我在博文中已经明确说了，这个超分辨荧光显微镜肯定获奖，Stefan W. Hell（我还翻译成阎王爷先生）是我看好的。但是，另外两个的技术我也简单评论过，不够靠谱。还有一位华人，庄晓威，我明确说过不行，等她抹鼻涕去吧！
同时明确宣告：双光子显微镜正式出局。
2012-10-4， 我看到的一些诺贝尔奖级别的成果和工作 （http://blog.sciencenet.cn/blog-99360-619316.html）
这里有位博主，北大的席鹏，对这个技术有详细的科普，整个系列。
（看到他的博文了：有感于超分辨获得2014诺贝尔化学奖）
不需要看诺奖委员会的获奖理由了，我简单介绍几句。
光学显微镜有个分辨率的极限问题，大概是半个光学波长，比这个波长更小的物体，就分辨不出来了，比如使用400纳米的光，分辨率就是200纳米左右。这个极限大概19世纪就知道了，最近二十年才被打破，所以意义重大，所用的手段是纯粹的物理学，所以说今年的化学诺奖是物理学的胜利。
以前有双光子显微镜，可以稍微低于这个分辨率极限，但是实际上就在极限上工作。所谓的超分辨率荧光显微镜，就是打破了这个分辨率的极限，比如还用400纳米的光，可以容易分辨200纳米以下的物体，甚至可以达到20纳米。
以前的显微镜总是用一束光，这束光是一根细丝，聚焦到一个很小的小点上，这个小点就是分辨率极限。由于光的衍射效应，这个小点的大小受到光的波长的限制。这也是自从人类发明光学显微镜以来，困扰了200多年的难题。
阎王爷先生的超分辨荧光显微镜叫做STED, 基本原理是用两束光，实际上是两束激光，一束是正常的光聚焦到一个小点上，下图左边，这个就是衍射极限的最大分辨率；另一束激光变成中空的筒子一样，下图中间；两束光聚焦到同一点上，由于第二束光把第一束光给灭了，只有中间那点没有灭掉，所以才能看到，这个更小的小点就是新的分辨率，打破了衍射极限，下图右边。这就是这个项目的重大意义所在。
这样，使用这样的光学显微镜就可以清楚看到更小的物体，比如纳米材料的形貌，更广泛的应用是在生物学领域，比如下图，等待生物学专业人士来科普。
顺便说一句，中国目前是否有这样的超分辨光学显微镜我还不清楚，北大的席锋那里可能有，质量和运性情况不知道，其他单位没有听说过。
比这个显微镜更低档一点是，双光子显微镜，所用的激光就是飞秒激光，国内估计总共有50台左右，价格每台300万到600万元，全部西方制造，只有五家公司：尼康，奥林巴斯，莱卡和蔡斯等。
更低一点档次的显微镜是激光显微镜，每台大概200万元，国内估计200台到300台之间，只有西方制造。
还有电子显微镜，分辨率可以达到0.1纳米或许更小，远远比这个超分辨的光学显微镜高，但是各有优缺点。以后抽空再来评述。
有重要信息，会回来更新。
http://blog.sciencenet.cn/blog-376446-769256.html
周期结构有哪些呢？一维（线性）、二维（平面）和三维（空间）周期结构。关于波我们将它分成三类：标量波（例如电子运动的波函数）、矢量波（电磁波）、张量波（晶格波）。
【高等固体物理 笔记1】
这下麻烦了，更加落到我的领域范围之内了，不得不说点。
[13]刘全慧
2014 Nobel Prize in Chemistry
The Nobel Prize in Chemistry 2014 was awarded jointly to Eric Betzig, Stefan W. Hell and William E. Moerner "for the development of super-resolved fluorescence microscopy".
获奖原因：他们开发了超分辨荧光显微镜。
去年我在博文中已经明确说了，这个超分辨荧光显微镜肯定获奖，Stefan W. Hell（我还翻译成阎王爷先生）是我看好的。但是，另外两个的技术我也简单评论过，不够靠谱。还有一位华人，庄晓威，我明确说过不行，等她抹鼻涕去吧！
同时明确宣告：双光子显微镜正式出局。
2012-10-4， 我看到的一些诺贝尔奖级别的成果和工作 （http://blog.sciencenet.cn/blog-99360-619316.html）
6. 超级分辨光学显微镜
德国马普学会一家研究所的阎王爷先生 Stefan W. Hell 发明的STED 技术（Stimulated Emission Depletion Microscopy），我觉得是板上钉钉要得，不知道是那一年。同时和这个竞争的还有 STORM 和 PALM 技术。个人觉得后面两种以及变种不太靠谱，技术复杂后处理麻烦也不实用，纯粹玩玩而已。但是现在授奖很可能有纠结产生纠纷，因为给了第一个后面两个会有意见。反正大家都年轻，最好等几年，适者生存，如果后面的技术被时间淘汰掉了，诺奖委员会就好办了。
研究实现STED超分辨率光学显微成像，http://paper.sciencenet.cn/htmlpaper/20126281046454225044.shtm
7. 双光子荧光显微镜和非线性光学显微技术
双光子荧光显微镜的分辨率略微低于光学衍射极限，普林斯顿的3W大概1991年发明的，并申请了专利保护。这种显微镜非常实用，目前市场非常好。但是，你3W申请专利保护严重阻碍了市场的开发，后来的超分辨显微镜后来居上，青不是出于兰但是胜于蓝，你估计只有冷板凳了。你也去遗憾擦肩而过吧。
跟这个紧密相关的是著名华人Sunny Xie 的非线性光学显微技术，如果没有超分辨显微镜，可望和3W 分享。现在只能空留遗憾了。
总之，科学的进步不等人。
**********************************************这里有位博主，北大的席鹏，对这个技术有详细的科普，整个系列。
（看到他的博文了：有感于超分辨获得2014诺贝尔化学奖）
不需要看诺奖委员会的获奖理由了，我简单介绍几句。
光学显微镜有个分辨率的极限问题，大概是半个光学波长，比这个波长更小的物体，就分辨不出来了，比如使用400纳米的光，分辨率就是200纳米左右。这个极限大概19世纪就知道了，最近二十年才被打破，所以意义重大，所用的手段是纯粹的物理学，所以说今年的化学诺奖是物理学的胜利。
以前有双光子显微镜，可以稍微低于这个分辨率极限，但是实际上就在极限上工作。所谓的超分辨率荧光显微镜，就是打破了这个分辨率的极限，比如还用400纳米的光，可以容易分辨200纳米以下的物体，甚至可以达到20纳米。
以前的显微镜总是用一束光，这束光是一根细丝，聚焦到一个很小的小点上，这个小点就是分辨率极限。由于光的衍射效应，这个小点的大小受到光的波长的限制。这也是自从人类发明光学显微镜以来，困扰了200多年的难题。
阎王爷先生的超分辨荧光显微镜叫做STED, 基本原理是用两束光，实际上是两束激光，一束是正常的光聚焦到一个小点上，下图左边，这个就是衍射极限的最大分辨率；另一束激光变成中空的筒子一样，下图中间；两束光聚焦到同一点上，由于第二束光把第一束光给灭了，只有中间那点没有灭掉，所以才能看到，这个更小的小点就是新的分辨率，打破了衍射极限，下图右边。这就是这个项目的重大意义所在。
这样，使用这样的光学显微镜就可以清楚看到更小的物体，比如纳米材料的形貌，更广泛的应用是在生物学领域，比如下图，等待生物学专业人士来科普。
顺便说一句，中国目前是否有这样的超分辨光学显微镜我还不清楚，北大的席锋那里可能有，质量和运性情况不知道，其他单位没有听说过。
比这个显微镜更低档一点是，双光子显微镜，所用的激光就是飞秒激光，国内估计总共有50台左右，价格每台300万到600万元，全部西方制造，只有五家公司：尼康，奥林巴斯，莱卡和蔡斯等。
更低一点档次的显微镜是激光显微镜，每台大概200万元，国内估计200台到300台之间，只有西方制造。
还有电子显微镜，分辨率可以达到0.1纳米或许更小，远远比这个超分辨的光学显微镜高，但是各有优缺点。以后抽空再来评述。
有重要信息，会回来更新。
http://blog.sciencenet.cn/blog-376446-769256.html
周期结构有哪些呢？一维（线性）、二维（平面）和三维（空间）周期结构。关于波我们将它分成三类：标量波（例如电子运动的波函数）、矢量波（电磁波）、张量波（晶格波）。
【高等固体物理 笔记1】
||
在总结第一次和第二次上课的笔记之前，让我们思考一个问题：什么是物理学？当然这个问题问不同的人会有不同的答案，那么在这里我给出我自己的答案，供大家参考和拍砖。我认为的物理学是“考察自然界中物质的性质和演化的科学”。既然是物质，就一定会有组成和性质；既然是演化，就一定会有演化的规律。这两个问题基本涵盖了物理学中的绝大部分领域。也是我们下面整理的一个重点。
为什么我们要这么来做呢？毕竟高等固体物理这门课主要研究的是固体物理或者更广泛一点的凝聚态物理中物质的性质以及它们可能发生的演化方法。在物质性质中，我们比较常见的有：力学性质、热学性质、光学性质、电磁性质等等。而演化中往往是在一定条件下所进行的，因此我们要探究物质的演化规律。因此整个高等固体物理讲述的是这么一件事：“在凝聚态物理框架下探究物质的物理性质及系统演化规律的学科”。前面的废话先说到这里，下面让我们一起进入高等固体物理的课堂当中吧。
注1：因为下面所说的是笔记中的重新整理，可能叙述顺序可能与一般书本上的不太一样，当然这也带有了我个人的风格和理解在里面。我尽量把语言变得通俗一点，能不使用公式的地方尽量不适用ugly的大长串公式（一方面是为我个人方面，另一方面也许有些读者可能在手机上观看，并不一定能很好的显示公式。但是如果非要有公式的话，我也会截图放到上面的。）。相关的数学推导会用PDF形式做好放在附录中。欢迎大家下载。不过如果想自己先推导的话，我当然是比较赞赏这种做法的啦！
注2：我自己的理解和感悟都用蓝色表示。正规的叙述用黑色表示。这样如果大家不想看我自己的评论的话，可以只看黑色的部分即可。
第一部分：课程概要
本课程中的老师、助教、如何考试、如何完成作业、project怎么做（BALABALA.......）。没有什么好记录的，因此舍去。
在这里给出老师建议的参考书：
1.阎守胜，固体物理基础，北京大学出版社(2011)
2.冯端、金国钧，凝聚态物理学，高等教育出版社(2013)
3.NRC，90年代物理学---凝聚态物理学，科学出版社(1992)
4.张礼, 近代物理学进展, 清华大学出版社(2009)
5.P.W.Anderson, Basic notions of condensed matter physics, Benjamin/Cummings,Menlo Park (1984)
6.P.M.Chaikin & T.C. Lubensky, Principles of condensed matter physics, Cambridge (1995).
7.Gerald D.Mahan, Condensed Matter in a Nutshell, Princeton (2011)
8.李正中，固体理论，高等教育出版社(2002)
第二部分：范式的建立与固体物理的范式
在科学的发展之中，范式的概念在起着很重要的作用。这一部分也许应该算在科学史当中，但是它对于下面行文的思路会有很大的帮助。因此把它放在这里也未尝不可。范式的概念是Thomas Kuhn在Harvard读理论物理博士的时候所提出的概念，记录在《The Structure of Scientific Revolutions》这本书当中。那么什么是范式呢？范式通俗来讲就是一个学科的结构，一个学科的灵魂性的概念和架构。那么科学在发展的时候避免不了6种情况：前范式阶段、常规科学阶段、反常阶段、危机阶段、科学革命阶段、新范式阶段。理解起来也很容易：当一个学科处于混沌状态的时候，只有只言片语的实验数据和理论，这时为前范式阶段；而当理论发展、实验数据越来越多的时候，有人就开始将理论搭建成一个框架（当然还不完善），并依据这个框架开始进行实验的指导以及理论的进步，这时称为常规科学阶段；当更多的实验现象被发现后，往往可能有一些现象与框架所预计的不相符合，这时可能能用一些策略解释，并没有对框架的根基产生什么影响，因此这时称为反常阶段；而当有决定性的实验事实被发现的时候（例如迈克尔逊莫雷实验），理论框架的根基产生了动摇，这时人们就要寻找新的范式或者在原有框架上进行修修补补，这样就进入了危机阶段；会有很大多数的人在这个时候参与到修修补补的工作当中来，他们中的几个人发现了新的范式或者是给出新的思路的时候，那么科学革命阶段将要开始；当新的范式被建立起来以后，人们又将进入下一个范式转换的轮回当中。科学就在这无穷无尽的范式转换中得到长足的发展。
我们以固体物理为例（毕竟它是我们高等固体物理的基础）：固体物理的范式可以写成下面的样子：
“周期结构中波的传播规律”（1946年Brillouin的著作中有提到）。在这个范式中，我们可以看到两个概念：周期结构以及波。那么周期结构有哪些呢？一维（线性）、二维（平面）和三维（空间）周期结构。关于波我们将它分成三类：标量波（例如电子运动的波函数）、矢量波（电磁波）、张量波（晶格波）。下面就针对这些不同周期结构以及不同种类波进行讨论。Here we go!
Case 1：标量波（电子波函数）
在研究标量波的时候，我们以电子波函数为例。以多原子体系为例，每个原子核都会对电子有吸引作用，而电子之间会有排斥作用。在这个时候如果求解整个体系的准确Hamiltonian将会非常的困难（Hamiltonian写出来将会非常的长，而且其中会有很多的相互作用）。为了解决这个问题，Born和Oppenheimer提出了著名的B-O近似：将电子运动和核运动分离。核运动可看做经典力学，电子可看成外电场。而电子的运动则可以看做是在核所形成的势场当中所得到的薛定谔方程。这将系统的求解大大的简化了。但是依旧我们要处理的是多电子波函数。而这个是不好deal with的。因此我们下面又会用到单电子近似，也就是将单独的电子拿出来，针对它来说的话核对它的作用可看成势场；同样周围其他电子对它的作用也可以看成另外的势场（与核的吸引相反的排斥势能），这样我们就可以将多电子波函数转化成单电子波函数，得到了“单电子近似”。这时可以得到每个电子所处的能级的能量。然而当我们将很多的电子能级结合在一起的时候，它们就会形成一个带状结构，我们称它为“固体能带”。关于固体的性质很大程度上依赖于固体内部的能带结构。因此如何计算固体的能带结构，是固体物理课程的首要重点。（Question：电子波函数能求出来物质的何种性质？）
Case 2：矢量波（电磁波）
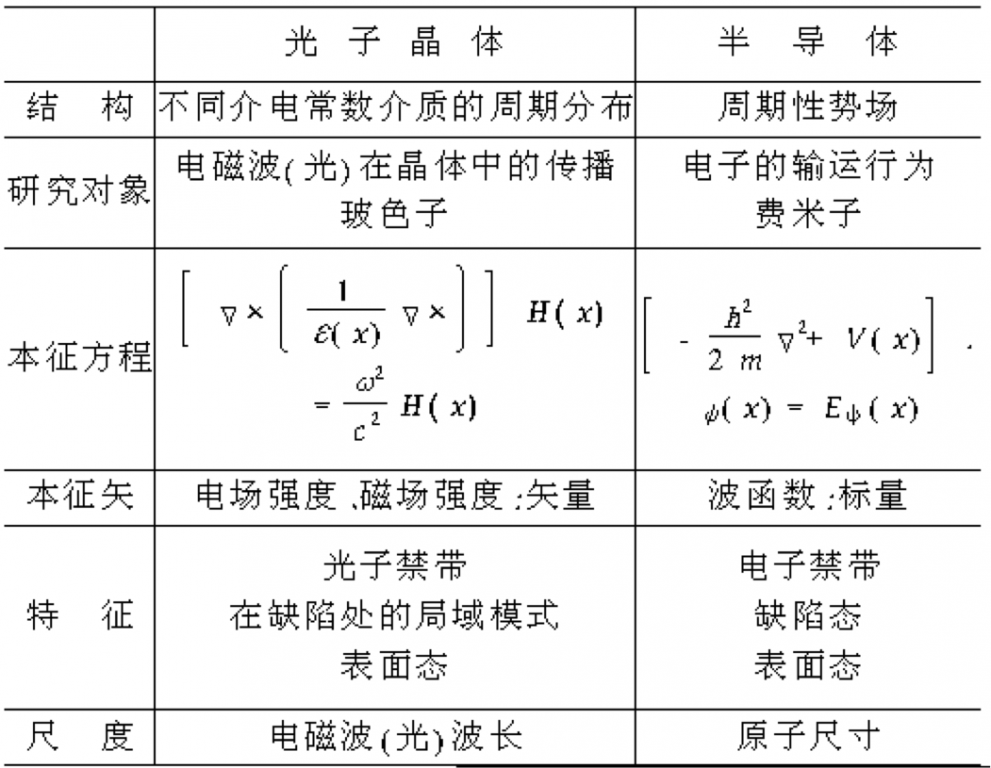
电磁波在固体中的运动可以得到物质的电磁性质或者光学性质。一个很重要的应用就是X衍射动力学。另外一个比较有趣的物质是光子晶体。既然电磁波可以在物质中传播，而光又是一种电磁波，那么能调节光在物质中的传播，那该多好。在1987年E.Yablonovitch在论文（PRL58，2059）中第一次提出了光子晶体的概念。在1990年的另外一篇文章（PRL65，3152）中从理论上预言了第一个有完整光子带隙的三维光子晶体。在1991年第一次在实验室用实验方法制备了有完整光子带隙的三维光子晶体，从而打开了光子晶体研究的大门。现代的光子晶体大多是人工设计、制备的。然而大自然中也有很多的光子晶体：蛋白石与蝴蝶翅膀。电磁波在周期型结构中所遵循的规律仍旧是Maxwell方程组，唯一不同的是加上了Bloch波的概念（周期波）。当一个光子晶体有了带隙以后，那么处在这个带隙频率中的光就无法通过光子晶体。它和半导体有很多的相似之处，下表就说明了它们之间的对比：
光子晶体有着很广泛的应用。例如做光子晶体光纤。我们知道，一般的光纤有如下的缺点：（1）有损耗和色散（2）单模光纤的直径较小（3）单模波长是有限的（4）特定的工作波长才可以使用。而光子晶体在这些方面都有着很大的优势：（1）无损耗、而且色散可根据光子晶体的结构来进行调制（2）已经可以制造大半径的光子晶体光纤（3）在光禁带范围内所有的波长都能进行单模工作。（Questions：（1）为什么单模光纤的直径比较小？（2）如何根据结构来调制色散？具体应该如何做？（3）何为单模工作？）另外可以运用到光子晶体的地方是改变原子的自发辐射速率。因为自发辐射速率是正比于光子态密度的。因此通过光子晶体改变光子的密度就可以改变自发辐射的速率。当处于光子晶体的原子的辐射频率落在完全光子能隙（Question: Explain this）中自发辐射被抑制，而落在不完全能隙中时自发辐射的速率被改变。对于完整的光子晶体来说，它的能隙是连续的。而对于其中有缺陷的（例如点缺陷（光子晶体微腔）和线缺陷（光子晶体波导））来说，会有一个缺陷模的存在，这个缺陷模的存在导致在能隙中的某些波长的光会透过光子晶体。
在普通光纤中，信息的传输如果想要转弯是需要很高成本的，因为普通光纤是运用全反射来进行传输的，而当出现偏转的时候就信息就会有遗失，这样要使得信息完整性得到保证的话，所用的光纤长度将会非常的长，成本会很高。但是光子晶体中可以使用一些缺陷位或者是线缺陷来调制光的行走路线。目前已经有实验进行了验证，效果比较好（PRL1996，77，3787 & Science1998，282：274）。并且也可以调制光子晶体去做门电路：进来频率的光为f1,f2,f3经过光子晶体之后只剩下了f1,f2。f3被吸收掉了。我们可以用这种性质来做“门电路”，因此可以进行逻辑运算，进而做出来光子晶体为主的计算机。当然要准确的计算出来光在光子晶体中的运动的话，需要求解带边界条件的Maxwell方程组，比较成熟的方法是使用时域有限差分方法。光子晶体还可以用来做信息的处理元件。将同一线路的信号进行分流。总而言之它的用处非常的大。
当然，这么好的性质是要付出代价的。上帝对所有人和物都是公平的。光子晶体所存在的问题有：
（1）制备Band Gap在可见光波长范围内的光子晶体还比较困难
（2）在任意位置上引入所需要的缺陷目前的技术还无法达到。（理论上的预期也不会太容易吧？）
（3）解决高效率光子传导材料的技术问题
（4）如何将现在的电流、电压加在光子晶体上的问题：因为我们要做器件的话，还是希望它用电比较的好。当然可以引入光电转换器来进行，不过具体的问题我也不是太清楚。得专门做器件的人才能知道。
在这里也可以谈谈科学与技术的问题。任何技术的发展都离不开基础研究，但是如何正确的对待科学和技术的区别，也是很重要的。在科学上我们只在乎Why和If的问题（为什么会这样？如果那样的话会怎样）而在对于技术的时候，我们需要考虑的就是How和What的问题（要做成什么样？怎么做？有什么用途）。两者的着眼点很有差别，在这里我想提一下。
Case 3：张量波（晶格波）
在这里我们讨论的是晶格的振动。晶格振动影响着固体的热学性质（比热、热导率等等）。最常见的模型就是一维原子链模型，具体的模型计算将会在附录中给出。当我们计算以后会发现有两种性质的色散关系。一种在原点左右的变化状态为线性的，而另外一种的斜率几乎为0。我们称线性部分为“声学支”，而斜率为0的部分为“光学支”。对于一个3维晶格来说，如果有N个原子，那么总的自由度为3N。在这3N个自由度中，能形成声学支的只有3个方向的（x,y,z），因为只有3个声学支。而剩下的3N-3个自由度都是光学支。
在我们讨论完三种case的波在周期性结构中的运动之后。下面我们就要谈论一下如何从固体物理推广到凝聚态物理当中。在固体物理中我们选择的是周期性结构。而在凝聚态物理中我们往往需要考察的体系都是局部无序或者整体无序的（在无序这章中有涉及）。而且研究内容从固体扩展到了非晶、液晶、准晶和液体当中。在性质的研究中也从原来的表观物理性质开始探究量子的相干性（相互作用体系）（例如输运性质）。在以后的课程中还会讲到凝聚态物理的范式：对称性破缺。对称性是一个系统十分重要的整体性质。
第三部分：量子化学的范式
化学从古到今都被人说成是“瓶瓶罐罐+摇摇晃晃”。但是当Kohn和Hohenberg提出来了密度泛函理论之后，化学将从原来的纯实验科学向理论与实验密切结合的科学发展。分子和原子属于量子力学所研究的范畴。而且一般的化学体系都是多粒子体系，因此从理论化学的发展可以看出多粒子体系应该如何处理。下面从价键理论到分子轨道理论分别介绍。
价键理论可以说是最基础也是最有效的化学理论。利用量子力学的观点来看，当一个体系写出了Hamiltonian的时候，下面的事情就是求解本征方程。目前来说价键理论最常用的就是使用变分法来进行求解（针对于H2来说）。变分波函数为电子在不同轨道上的排列。在有机化学当中会有杂化轨道这么一说。当然相信大家对于价键理论以及杂化轨道理论这种东西在高中或者大学化学中都学过了。因此在这里不再赘述。
分子轨道理论的基本思想是：电子在整个分子上有分布，这时的波函数为多电子波函数。而分子轨道是原来原子轨道的线性组合。能有效行程分子轨道的条件：（1）能量相近（2）对称性匹配（3）最大重叠。
第一节课和第二节课的笔记就记录在这里。未完待续，以后还会有更多更精彩的内容奉献给大家。欢迎持续关注。
附录一：一维原子链中晶格振动模型的求解
附录二：用变分法处理H2体系，得到正确的解
本征态都必须满足线性叠加原理
量子计算的最终结果只能由测量给出，因为你没有别的信息来源。所以，既然要完成计算，当然必须要实现通过设计让最终测量得到的结果就是计算的结果。坍缩必然会被考虑，利用它，或者让最终态处于本征态上。
GR的一个特点，就是它的非线性：能动张量决定了度规，但是能动张量本身又是需要由度规来决定的。
在GR与QM的结合过程中，这种非线性就很严重了：QM中系统能量是量子化的，从而存在能级与能态的概念，从而才有量子态，以及定态、本征态等概念。所有的本征态都必须满足线性叠加原理，这是QM的基本要求。但是不同的本征态的能量肯定是不同的（这里不考虑能量简并，而且也不可能所有本征态都简并到一个能量本征值上吧……），从而他们对应不同的时空（能量不同，能动张量不同，那么时空度规肯定不同——能动张量相同的时空度规不一定相同，但能动张量不同的时空度规肯定不同），而时空本身是非线性的，因而不同本征态对应了不同的时空，而且不满足线性叠加原理，从而破坏了量子力学的最基本的假设：线性叠加原理。从而，要么你承认GR放弃QM，要么你承认QM放弃GR。
破裂从此诞生。
相对论与量子力学的矛盾
本征态都必须满足线性叠加原理
量子计算的最终结果只能由测量给出，因为你没有别的信息来源。所以，既然要完成计算，当然必须要实现通过设计让最终测量得到的结果就是计算的结果。坍缩必然会被考虑，利用它，或者让最终态处于本征态上。
GR的一个特点，就是它的非线性：能动张量决定了度规，但是能动张量本身又是需要由度规来决定的。
在GR与QM的结合过程中，这种非线性就很严重了：QM中系统能量是量子化的，从而存在能级与能态的概念，从而才有量子态，以及定态、本征态等概念。所有的本征态都必须满足线性叠加原理，这是QM的基本要求。但是不同的本征态的能量肯定是不同的（这里不考虑能量简并，而且也不可能所有本征态都简并到一个能量本征值上吧……），从而他们对应不同的时空（能量不同，能动张量不同，那么时空度规肯定不同——能动张量相同的时空度规不一定相同，但能动张量不同的时空度规肯定不同），而时空本身是非线性的，因而不同本征态对应了不同的时空，而且不满足线性叠加原理，从而破坏了量子力学的最基本的假设：线性叠加原理。从而，要么你承认GR放弃QM，要么你承认QM放弃GR。
破裂从此诞生。
相对论与量子力学的矛盾
相对论与量子理论的联姻主要分两步：
首先是SR与量子力学的融合，然后是GR与量子力学的融合。 前一步很早就完成了，那就是量子场论。而且我们在融合的过程中发现了自旋的重要性与重要贡献，可以说是让大家喜出望外的一件事情。 但是GR与量子力学的结合却迟迟无法得到实现，让我们非常遗憾。 下面，我就现在GR与量子力学的一些主要矛盾简要地说一下。 GR的一个特点，就是它的非线性：能动张量决定了度规，但是能动张量本身又是需要由度规来决定的。 在GR与QM的结合过程中，这种非线性就很严重了：QM中系统能量是量子化的，从而存在能级与能态的概念，从而才有量子态，以及定态、本征态等概念。所有的本征态都必须满足线性叠加原理，这是QM的基本要求。但是不同的本征态的能量肯定是不同的（这里不考虑能量简并，而且也不可能所有本征态都简并到一个能量本征值上吧……），从而他们对应不同的时空（能量不同，能动张量不同，那么时空度规肯定不同——能动张量相同的时空度规不一定相同，但能动张量不同的时空度规肯定不同），而时空本身是非线性的，因而不同本征态对应了不同的时空，而且不满足线性叠加原理，从而破坏了量子力学的最基本的假设：线性叠加原理。从而，要么你承认GR放弃QM，要么你承认QM放弃GR。 破裂从此诞生。 然后还有一些别的因素。 比如，GR中时空是可以互换的，这就是经典的Lorentz变换。但是在QM中时间与空间是严格区分开的。Schrodinger方程就是如此，对时间是一阶的而对空间是二阶的（当然，场论中并不是如此，不过也有类似问题）。 这个在做量子化的时候就凸显了出来：量子场论中的正则量子化是已经人为地将时空分为了时间与空间的。 虽然我们可以要求这种分割以后的系统依然具有Lorentz对称性——这点在广义相对论的正则表示（Dirac发展出来的）中有过仔细的研究——但是这种分割方法本身还是意味着一种不协调。 当然，我们可以用协变量子化（比如圈量子引力就是如此），但是协变量子化也有自己的问题。 最后来说一下，那就是纯数学上的“暗示”了。 目前所有的引力量子化方案，都被证明在两圈图层面上是发散的，也就是不可重整。不可重整就表明了我们还有很关键的东西不知道，而这个不知道的东西如果继续不知道的话，那说统一GR与QM就有点不可思议了。 当然，可重整也不代表我们什么都知道了…… 超对称等一系列手段可以消除两圈图层面上的发散，但是在更高的全图上大家也一致认为还是会发散的，因而现在的量子引力必然是不可重整化的。当然，可以很自我安慰地认为更高圈的不可重整化只发生在Planck尺度上，但至少就表明了我们对那个区域的物理还有很多不知道。
关于引力在量子场论中的不可重整，这里要多说几句。
在量子场论中，我们知道一般的树图都是非发散的，但是圈图很可能会发散。发散也分两种：一种是表征发散，一种是非表征发散。如果一张图可以通过断掉一根内线而分解为互不联通的两部分，那么这种图称为单粒子可约的（1PR），反之则是单粒子不可约的（1PI）。1PI的表征发散是精准的，因而我们主要可以用1PI图的表征发散来研究整个场论的发散情况。
而1PI表征发散的计算，借助图论知识，我们知道可以约化为（不同粒子的）外线数、圈数和顶角数的代数关系。
在场论中，我们发现，如果跃迁振幅随着图的复杂性的上升，其发散项数量也上升，那么这种场论就是不可重整的；而如果随着复杂性的上升，发散项保持恒定，那么这种场论是可重整的；最后，如果对这图复杂度的上升，发散项的数量反而减少，那么这种场论就是超可重整的。
在场论中，这种图的复杂程度就体现在顶角数和圈数上，其中顶角数可以被证明是最主要的（可以将圈数约去）。
因而，如果1PI图随着自身顶角数的增加，发散项增加，那么这个理论就是不可重整的；保持不变，则是可重整的；发散项减少，就是超可重整的。
对于我们熟知的理论，四维中的Phi4理论和QED都是可重整的，二维Phi4理论是超可重整的。
而对于引力，我们的研究发现，是不可重整的。这是虽然对于0自旋粒子还是1/2自旋粒子，引力作用顶角是2+1型的（两根粒子线一根引力线），但是对于引力本身，顶角是2+2的（四根都是引力线），而这种顶角增加发散项。从而，引力是不可重整的。事实上，在有些模型中，引力与粒子的作用顶角也是2+2的，从而这种顶角也是不可重整的。
由此可见，在现有方案中，量子引力是不可重整的。
white 对于任一个区域上所有点构成的集合,可以定义该点集合的测度为该平面空间区域的面积
二阶方程的初始条件或者边界条件是容易具有明确的物理意义的，零阶是位置，一阶是动量，一般性的物理经 第一章 引论 - 上海交通大学科学史与科学哲学系
shc2000.sjtu.edu.cn/phy/phy1.htm
上述依存关系是每一物体实际上都承受着来自无数个其它物体各个方面的引力这一情况的抽象。古典力学按照把两个物体的抽象的图景向着三个物体的更为具体的 ...轉為繁體網頁 phymath999: 体系对质点的引力,只与这两质点有关,与第三者 ...
phymath999.blogspot.com/2015/03/blog-post_32.html
2015年3月17日 - 牛顿linear: 速度是加速度在时间上的线性叠加作用在一个粒子上的力是其他粒子的轉為繁體網頁 "牛顿把下述规律宣布为宇宙的原理，即两个物体以与其质量成正比与其距离的平方成反比的力相互吸引。上述依存关系是每一物体实际上都承受着来自无数个其它物体各个方面的引力这一情况的抽象" "第9章静电场_百度文库
220.181.112.102/view/6d67692f647d27284b7351f6.html
轉為繁體網頁
应该特别指出，从十九世纪物理学的基本原理中发展出来的，复杂的运动形态不可归结为简单的运动形式的思想，世界的无限复杂性的思想，以及其规律的非线性的思想，这些思想如此鲜明地反映于哲学和十九世纪科学思维的风格中，并且与上个世纪的情况完全不同。对十八世纪的文化来说是以其思想的单义性为特征的，也就是一个现象严格地，精确地依赖于另一个现象的观念。这种观念最高级的表现就是著名的拉普拉斯的最基本的模式，它的意思就是知道宇宙全部质点的位置和速度就可以预言日后自然界的发展过程和人类命运直至历史的和生活习惯的细节[2]科学就是把现象从宇宙间无穷尽的总体联系中人为地抽取出来并安置在原因——结果的链条之中。按照席勒的说法只有“纵的联系”才会使科学发生兴趣，而同时也就抛弃了使单纯的依存关系走样和复杂化的“横的联系”。此时的科学虽然意识到这种“横的联系”，但是依然力图把它分割为单纯的“纵的联系”。牛顿的引力论和摄动论就是一例。牛顿把下述规律宣布为宇宙的原理，即两个物体以与其质量成正比与其距离的平方成反比的力相互吸引。上述依存关系是每一物体实际上都承受着来自无数个其它物体各个方面的引力这一情况的抽象。古典力学按照把两个物体的抽象的图景向着三个物体的更为具体的图景进行过渡，同时把第三个物体认为是使原来的简单的情况变得复杂起来的摄动的根源。需要指出：在真空中就是两个物体也算得上是一种复杂的具体的图景。第一步抽象是一个在真空中运动的孤立的物体。这个物体作匀速直线运动，其坐标是时间的线性函数。在宇宙力学图景的发展过程中每迈出新的一步都要回复到空间量与时间量的线性依存关系上来。那种线性化是以向较小的区域过渡而被实现的。在只有一个孤立的运动物体的最早的图景中（这正是机械论的自然科学的终极抽象），物体的位置是线性地依赖于时间的空间量。后来以牛顿为代表的自然科学考虑到开普勒定律和天体的加速度，并认为此加速度就相似于地球上物体的加速度，这样就从《自然哲学原理》中第一定律过渡到第二定律。但是，用匀加速运动代替加速运动，用现代的术语来说就要处于均匀力场之中，这时速度也就成为时间的线性函数了。这种先把坐标对时间的一阶导数线性化然后二阶导数线性化的意图表征牛顿力学的特点。从坐标开始，以后是速度，加速度等等，都被认为是时间的线性函数，线性化也成为数学分析的基础。科学只对所研究量的线性关系感兴趣，并引入微分的概念（函数增量的线性部分），和导数的概念（包含在无限小区域内增量的比值）。从宇宙间现象的不可胜数的联系中，抽象地提取出所要研究的量，这种抽象过程合理到什么程度，这些有限个量之间的联系特征也就是与实际符合到什么程度。当力场可以忽略时在惯性作用下匀速运动的图景是与物体的实际情况相一致的；在研究均匀力场时，匀加速运动的图景是与实际情况相一致的。数学的概念鲜明地显示出抽象分析的每一步的约定性。当哲学上对自然科学的知识进行概括以后，这样的一种约定性就变得可查觉的了。然而这种经常进行的认识过程一旦被绝对化后，有条件的抽象看起来就像是现实之中无条件精确的等价物了。
量子力学中的谱测度与概率测度 对算符F求平均值：<ψ|F|ψ>，它等于F的本征值f(i)乘以取该本征值的概率P(i)，再求和: <ψ|F|ψ>=∑ f(i)P(i) （1） 但我们可以把这个方程两边同时剥去外衣<ψ|和|ψ>，直接露出赤裸裸的算符F本身，得到 F＝∑ f(i)μ(i) （2） 此时，称μ(i)为算子F的谱测度，上式称为算符F的谱分解。本来，矩阵也好，算子也好，谱分解不过是一个纯粹的数学事实，但是量子力学中，波函数（如果以|ψ>代表Hilbert空间中的矢量，那么通常所说的波函数，即是Hilbert空间中的泛函）代表概率幅，这使得(2)式所表示的谱分解，有更多的含义。例如在（2）式中，F的“算符性”由μ(i)来承载，因为本征值f(i)只是一个c数不是算符，而 <ψ|μ(i)|ψ>=P(i) （3） 从（3）式看，即算符μ(i)的平均值就是概率P(i)。因此谱测度μ(i)相当于一个概率算符！如果前面的求和是连续求和，那么谱测度μ(i)相当于一个概率密度算符。 （为了配合与季候风兄的讨论，我在众数学高手面前班门弄斧，向非数学专业人士科普一下一些基本概念。可能难免会含有诸般错误） 1. 测度 通常的函数是以某个变量为自变量的函数。而测度可以看作是一种以集合为自变量的“函数”（映射，映射是比函数更一般的概念）。即给定一个集合，就让某个量与之对应，这个量就是集合的测度。当然测度的定义域——由集合构成的集合，必须满足某种代数性质(σ代数),这种代数常常作为测度的一种定义方法. 例如,由所有事件集合构成一个集合(因而是集合的集合),它可以作为概率事件的样本空间.此时定义在事件集合上的测度,可以是这个集合中所有互斥的基本事件发生的概率之和.因此概率就是一种测度.此时概率论要求σ代数自然满足. 再如,由一些平面空间区域(相当于点的集合)构成一个集合(要求满足σ代数哈),对于任一个区域上所有点构成的集合,可以定义该点集合的测度为该平面空间区域的面积  . 物理学中,有时把一些积分的微分元直接称做积分测度. 一个点,一根线的面积为零,所以在二维面积测度的意义上,点和线的测度都是零.定义一维区间长度为该区间上点集合的测度.不难看出,此时可数无穷多个点的集合测度为零.那么,不可数无穷多个点的集合测度是不是一定大于零呢?不一定!例如康托分形集合就是测度为零的、包含不可数无穷多个点的集合。 测度理论,是现代公理化概率理论的基础.研究某些比较深入的量子力学问题,还非得用基于测度理论的概率理论才行.测度理论可以使得黎曼积分被推广。可以看到，上面的测度例子都是正定的，这也是概率可以作为测度来描述的一个重要原因。但是有时候，例如我们需要考虑负的积分结果，此时可以引入广义测度的定义。相对论量子力学产生负概率问题，人们选择的办法是避免它。由于负概率来源于正反粒子同时存在，也许可以直接引入负概率概念来描述。例如正电子出现的概率为正，同一情况下让负电子出现的概率为负。问题是，此时概率的归一性不好办（即总概率如何定义？通常为1）。也许还是有办法，但是也许不必了，因为量子场论很成功地替代了相对论量子力学。 2. 量子力学中的谱测度与概率测度 对算符F求平均值：<ψ|F|ψ>，它等于F的本征值f(i)乘以取该本征值的概率P(i)，再求和: <ψ|F|ψ>=∑ f(i)P(i) （1） 但我们可以把这个方程两边同时剥去外衣<ψ|和|ψ>，直接露出赤裸裸的算符F本身，得到 F＝∑ f(i)μ(i) （2） 此时，称μ(i)为算子F的谱测度，上式称为算符F的谱分解。本来，矩阵也好，算子也好，谱分解不过是一个纯粹的数学事实，但是量子力学中，波函数（如果以|ψ>代表Hilbert空间中的矢量，那么通常所说的波函数，即是Hilbert空间中的泛函）代表概率幅，这使得(2)式所表示的谱分解，有更多的含义。例如在（2）式中，F的“算符性”由μ(i)来承载，因为本征值f(i)只是一个c数不是算符，而 <ψ|μ(i)|ψ>=P(i) （3） 从（3）式看，即算符μ(i)的平均值就是概率P(i)。因此谱测度μ(i)相当于一个概率算符！如果前面的求和是连续求和，那么谱测度μ(i)相当于一个概率密度算符。 在通常的量子力学中，谱测度μ(i)被称为投影算符，因为它是幂等的（它的平方等于它自己），而且利用它可以实现将某个矢量向μ(i)中包含的某个矢量上进行投影。与此相应地，传统量子力学中，要求可观察量对应的算符是自共轭的，这类算符的谱分解中，谱测度对应投影算符。 但是传统量子力学存在局限性，需要扩展。比如，我们的测量，不一定对一个系统整体进行测量，而是对一个系统中额达某个子系统进行（严格说来，我们无法把观察者和被观察对象分离开来），此时算符的谱分解中，谱测度不一定对应投影算符。再例如，有些可观察量，例如时间，相位差等等，它们并不对应自共轭算符。 为了推广量子力学可观察量的概念（即不一定对应自共轭算符），我们需要推广算符的谱分解（2），使得其中的谱测度μ(i)不必对应投影算子，而是把投影算子看作它的特例。由（3）式可知，谱测度相当于“概率算子”（或“概率密度算子”），因此，在正统量子力学中它对应投影算子只是一个偶然，这并不表明它直接与投影算子等同，它应该对应更一般意义上的“概率算子”（或“概率密度算子”），从而谱测度μ(i)可以一般地推广到“概率测度”。由于概率测度非负，所以此时的谱测度称为“正算子取值测度”（POVM）。只要谱测度μ(i)对应POVM，（2）式表示的算符，均对应可观察量，此时这样的算符不一定是自共轭的。 但是，为了与传统区分开来，谱测度常常是指可以解释成投影算子的那种。一个算符是谱测度意义上的，还是POVM意义的，关键取决于所取的Hilbert空间（即算符的表示空间）。有一个定理是说：每一个POVM，存在一个谱测度的“膨胀”（dilation）。例如，假定Hilbert空间H(1)是H (2)的子空间，算符F在H(2)中存在谱测度分解，那么它在H(1)上的压缩compression（或限制restriction）记为E，假定E在 H(1)中存在POVM分解，此时F是E在H(2)中的dilation。 需要提醒的是，dilation与扩张extension是两种概念，一个POVM意义上的算符，不一定存在谱测度意义上的extension，除非该算子的正负亏指数deficiency index相等。但是dilation就不存在这个限制：每一个POVM，都存在一个谱测度的dilation。换句话说，当闭对称算子的两个亏指数（deficiency index）相等时，才存在自共轭扩张（extension）。但是，如果这个算子存在POVM分解，则即使亏指数不相等，同样存在自共轭 dilation。
“朗道有序ψ参数”原本是一种适合描述唯象导电固体在极端低温下的波函数。可是，它又能用来描述超导体内部的欧姆电流和超导电流之间的相变。这就意味“朗道有序ψ参数”也能描述各种流体（气体和液体等等）。电流在导电固体内的热力学状态，通常被物理学家描述为“电子气”；而化学家则把它们描述为属于“离域键”性质的“金属键”。对于同一个自然对象，同时掌握物理学家和化学家的两种不同观点，以及不同的研究立场和量化方案，不仅对于自然科学专业的大学生（即本科生、硕士生和博士生的统一称谓）很重要，就是对那些不同专业领域内的职业物理学家和职业工程师，职业化学家和职业化工工程师，同等重要。
在超导物理学上，作为波函数的朗道“有序参量ψ”的平方，才有实验可测的意义。并且这个朗道“有序参量ψ”的平方的物理量纲是单位体积的倒数，这意味着朗道的“波函数ψ的平方”的物理含义是单位体积内的空间密度。
可是，在“薛定谔量子力学”中，“波函数ψ的平方”被大物理学家玻恩解释为发现“粒子位置的分布几率”（即原子核外电子位置的概率分布，俗称为“电子云”）。“波函数ψ的平方”是无量纲的一种函数，相当于数学量，而且是还是一种概率。
我们就是把“波函数ψ的平方”放大、特写，以便职业科学家和工程师，以及高等研究院所的师生，看清楚“波函数ψ的平方”的物理诠释的多样性，明白玻尔旗下举世公认的“哥本哈根学派”的权威释义，并不是唯一的。
为何非要是“波函数ψ的平方”才能获得物理意义呢？这是因为“波函数ψ”本身是一种“椭圆角度测度性的复函数”，而这种“椭圆复函数”在真实自然界中，仅仅基于它的几何性质，一直都被数学家和物理学家视为无法用任何科学实验来证实其存在性。而“椭圆复函数”的平方，即<ψ*|ψ>=|ψ|^2=r=实数，于是获得了科学实验上的可测性。
在自然界中，没有任何科学理由，“波函数ψ”总是一定被预先假定为这种“椭圆复函数”，而不能是别的什么性质的“几何函数ψ”，当然，它也可以是“凯雷-克莱因几何函数”，或者别的什么函数。类似地，在自然界中，“波函数ψ”也未必一定处处都必须被强硬地预先规定为“波函数ψ”，而不能是别的什么性质的“待定函数ψ”！“哥本哈根学派”对“波函数ψ”的权威解释，虽然是正确的，但是这种解释决不是什么“放之四海而皆准”的“普遍诠释”！比如，金兹堡-朗道方程中的“波函数ψ”的诠释，明显不同于“哥本哈根学派”对“波函数ψ”的权威解释。不仅如此，在我们看来金兹堡-朗道方程中的“波函数ψ”的诠释，应用更加广泛，而且<ψ*|ψ>的物理含义是单位体积内的空间密度，具有物理量纲。这种特殊的空间密度量纲，使得它不但可以直接被应用到“麦克斯韦电动力学”，“流体力学”领域中，而且还被直接应用到具有极大普适性的“热力学”中。由于<ψ*|ψ>的物理含义是单位体积内的空间密度，具有物理量纲。这使得“朗道有序函数ψ”本身也获得了一种“分数维度”（3/2维度）性质的空间量纲。这暗示着“金兹堡-朗道方程”代表着一种“物理分形几何学”。所以，种种迹象表明，在自然界中，决没有任何科学理由，只能接受“波函数ψ”一定被预先假定为是“椭圆复函数”，而不能是别的什么性质的“几何函数ψ”。
为了获得最一般意义上的“几何函数ψ”，把<ψ*|ψ>推广为<ψ*|S*ijSjk|ψ>，|ψ>被定义为离散有限维数或者连续无限维数的正变仿射空间，<ψ*|被定义离散有限维数或者连续无限维数的逆变仿射空间，S*ijSjk=Gik ，Gik为对称矩阵，学名为“度规矩阵”，或者“度规张量”。
科学家和工程师必须放弃“哥本哈根学派”对“波函数ψ”那种“唯一性”的权威解释，学会开拓视野，创建更加一般意义上的“普适量子物理学”。“哥本哈根学派”对“波函数ψ”那种“唯一性”的权威解释，在今天事实上不仅已经丧失了推动科学向前发展的动力，反而变成了一种强烈阻碍科学向前发展的阻力！在我们看来，“几何函数ψ”（我们不再使用传统上那种人为狭隘化的“波函数ψ”这个名称了）的物理含义，完全可以按照所研究的自然对象的量纲来约定。尤其是它的平方的量纲，即<ψ*|ψ>的量纲可以被约定为正好符合某个任意、但又是确定的物理量的传统量纲。
尤其是这种单位体积内的空间密度量纲的<ψ*|ψ>，有着极为广泛的直接应用。除了众所周知的电流密度
之外，我们可以随心所欲地定义类似的物理量。比如，一系列的唯象的宏观量子力学方程式：
伽利略量子引力场重力密度：f=<ψ*|mg|ψ>
牛顿量子作用力密度：f=<ψ*|ma|ψ>
洛仑兹电磁量子力密度：f=<ψ*|qE+qu×B|ψ>
量子电能密度：w(q)=<ψ*|qU|ψ>
量子磁能密度：w(Φm)=<ψ*|ΦmI|ψ>
量子理想气体状态方程压强：P=<ψ*|nRT|ψ>
……………………………………………………
诸如此类，我们可把现有的全部经典物理学的所有分支学科量子化！这是一场真正的科学风暴，它将以排山倒海、势不可挡的滚滚科学洪流的形式，彻底冲击涤荡现有全球所有中学和大学的科学教材和科学著作！这就是当人们打碎了“哥本哈根学派”对“波函数ψ”那种“唯一性”的权威解释的枷锁之后，直接获得“科学解放”，赢得“科学自由”，从未来回到现在的简单后果。
伽利略量子引力场重力：F=<ψ*|mg|ψ>
牛顿量子作用力：F=<ψ*|ma|ψ>
洛仑兹电磁量子力：F=<ψ*|qE+qu×B|ψ>
量子电能：w(q)=<ψ*|qU|ψ>
量子磁能：w(Φm)=<ψ*|ΦmI|ψ>
量子理想气体状态方程：<ψ*|PV|ψ>=<ψ*|nRT|ψ>
…………………………………………………………
诸如此类，我们照样能够把现有的全部经典物理学的所有分支学科量子化！彻底刷新升级现有全球所有中学和大学的科学教材和科学著作！这就是当人们打碎了“哥本哈根学派”对“波函数ψ”洞穴之见的“狭隘性”，而继续保留“几率统计诠释”之后，直接从未来回到现在所获得的一种“科学思想解放”和“科学思想自由”的简单后果。
跟弯曲有关的东西貌似都很喜欢空间的四阶导数→_→ 数学期望是一阶原点矩（表示分布重心）、方差是二阶中心距（表示离散程度）、偏态是三阶中心矩（表示分布偏离对称的程度）、峰态是四阶中心距（描述分布的尖峰程度，例如正态分布峰态系数=0） 二阶方程的初始条件或者边界条件是容易具有明确的物理意义的，零阶是位置，一阶是动量，一般性的物理经
统计学上的矩和物理上的矩，都是数学上的矩的特例，英語都是moment。
力矩看似好像和统计没关系，那不妨多加几个力，再看看公式。 设两个力F1和F2分别作用于位置r1和r2，力矩为F1 X r1 + F2 X r2 再看统计的例子，两个量x1和x2，相对权重为w1和w2，加权平均值为x1 w1 + x2 w2 现在看出相同了吧？力矩就是以力为“权”的，位置的加权一阶矩，当然这个权没有归一。 物理里还有一个moment，但是被翻译成了转动惯量[1]。 请自己看定义，统计上这是以质量为"权"的，位置的二阶矩。 现在给出数学上矩的定义[2]， 一个函数f(x)的n阶矩就是对(x-c)^n f(x)积分 简单起见，用了函数举例，其实用测度定义得更一般。 如果f(x)是分布函数，这就是统计矩了； 如果f(x)是力的分布，n=1，就是力矩了； 如果f(x)是质量分布，n=2，就是转动惯量了。 其他物理上的moment还有： 磁矩（电流的矩），角动量（动量的矩），电偶极矩（电荷的矩）等。 [1] http://en.wikipedia.org/wiki/Moment_of_inertia [2] http://en.wikipedia.org/wiki/Moment_(mathematics)
这个问题要从物理学、统计学和语源学三个角度回答。现在第一位的匿名用户认为物理和统计中的m矩都是数学概念的特例，这是对的。但历史上出现的顺序应该是物理moment -> 统计moment -> 数学moment，并且数学moment完全是对此的归纳，并不是起源。
先整理一下历史：力矩这个概念最早是由阿基米德提出的，著名的“给我一个支点，我就能撬动地球”就是关于力矩最著名的名言。 The works of Archimedes including On the Equilibrium of Planes which contains statics and levers, was translated into Latin by Gerard of Cremona (c. 1114–1187 AD). Therefore it seems likely that Archimedes used "moving power" to describe the effect of a lever in moving a mass on the other end, and being proportional to the product of the applied force and its distance from the fulcrum on the other end.最初的时候阿基米德可能是用”moving power“即”移动能量“来描述这一现象，后来在拉丁语被翻译成movimentum，到英语就变成了moment，中文翻译是矩。另一个容易混淆的概念是momentum, 中文一般翻译成动量，拉丁词源是momentum，意思也是"movement, moving power"。所以moment和momentum本来就是同源，只是到近代科学后被用来指代不同的物理量了。 moment更被人熟知的含义是“一瞬间”，这个意思可能是从momentum这个拉丁语来的，也有可能是从古法语里moment这个词来的。这个词汇发展到现在，在物理中和在生活中的含义已经很不一样了，但究其根源，都是”移动“的意思。 统计学里moment这个概念是从物理学引申出来的。前面的回答都给出了很好的定义，读者也可以参考Moments - Definition of Statistics Terms这里的解释。初学统计的人（包括我自己）往往对“moment”特别是中文翻译“矩”感到困惑，这丝毫不奇怪，因为它离原始含义“to move"或者“移动”已经太远了。 至于wikipedia上关于数学moment的概括Moment (mathematics)，我认为并不是太有意义。这个page里的reference和see also基本都是统计学的文献，可以说数学家一般是不会讲moment这个概念的。 参考资料： 1. Torque vs Moment 2. Meaning of the word "Moment"? 3. Online Etymology Dictionary 4. Moments - Definition of Statistics Terms 5. Moment (mathematics)
收起 |
1 yangwencao
发表评论 评论 (4 个评论)
- [3]霍东明
- 龚老师，我想问一下，什么是Majorana Fermion零模呢？
- 博主回复(2014-12-25 09:42)：Majorana fermion has energy = 0, so it also called zero mode.
量子力学中动量的定义是单位距离积累的相位，而不是质量乘以速度
Grotthus（1817）与Drapper（1843）在一个世纪以前提出的：“只有被分子吸收的光，才能有效地在这个分子中引起化学变化”的概括，被称为光化学第一定律。
显然在光化学中，进入反应池中的光必须与吸收此光的反应物或敏化剂的吸收光谱有一定程度的重叠，否则光不能被反应体系吸收，也就不能有效地引起分子的激发并发生光化学变化。而且值得着重指出的是，在严格的定量工作中，应当用这条定律逐个地检查所用光化学系统的各个部分。亦即不仅要知道光源的发射光谱、反应物的吸收光谱，而且应当知道所有的光学元件如透镜、滤光片、反应池窗口等的吸收光谱，还要知道溶剂与可能产物的吸收光谱。
光化学第二定律由Stark（1908—1912）与Einstein（1912—1913）提出。原来的说法是：
“每个由光引发化学反应的分子，从辐照光中吸收1个量子”
其后不久，他们又指出，这条定律只适于辐照后的初级过程。现在的说法是：
“分子对光的吸收是一种单量子过程，因而所有初级过程的量子效率之和为1”。量子效率的定义为：
定律中所指的初级过程可包括解离、异构化、辐射衰变（荧光及磷光）、无辐射衰变等。如以φi表示其i种初级过程的量子效率，则有Σφi=1。一般情况下，量子效率也可叫做量子产率。
这条定律适用于激发态寿命较短和中等强度辐照的情况。在高强度的光（如激光）辐照下，光子的密度可以达到1-102mol/m3。这时分子有可能吸收多个光子。
均匀吸收体系对单色光的吸收，一般用Beer-Lambert定律来描述。光化学中常用的形式是
式中I0-单位时间内入射到盛有浓度为c（mol/dm3）的反应池内壁光柱前端的单色光的强度（或量子数）。I-单位时间内透过长度为l（cm）的物质柱后光的强度。ε-称为摩尔消光系数（dm3/cm·mol）。对于给定的纯吸收物质在给定入射波长下为一常数。它是量子与分子相互作用条件下，对量子吸收几率的一种量度。
严格遵守上述关系式的条件是分子间的相互作用如缔合等，在给定浓度下可以忽略。
当吸收带较窄而照射光的波长范围相对较宽时，在整个分析光的谱带中ε并不保持为常数。对于包含不止一种吸收光的物质的均匀混合系，Beer-Lambert定律可以改写成
式中εi、Ci是与第i种吸收物质相应的摩尔消光系数及浓度。
繞射原理
當光通過一單狹縫時，如縫愈窄則光線會愈向兩旁擴張，此現象即所謂的繞射。如圖
1（A）為光通過一孔洞（孔徑大小遠大於光波長時），在螢幕上呈現出孔的光點（圖中水
平軸顯示出光強度大小），圖1（B）當隨著孔徑變小時，光的繞射現象便明顯呈現在螢幕
上。
A.單狹縫的繞射實驗
實驗目的
觀察光通過單狹縫時所產生的繞射現象，並測量亮、暗紋的位置和理論值相比較。
實驗方法
將雷射光射入單狹縫片，即可在狹縫另一側之螢幕看見繞射圖案。假設令狹縫的寬度
為b，中心點為O 點，狹縫口被均分成若干點，如圖2 所示。
P0 點光程差為零，稱為中央亮區。P1 點至狹縫頂點的距離比到狹縫底點的距離大一波
長λ，亦就是說P1 點到狹縫頂點的距離，比P1 點到O 點的距離大半波長(λ/2)，所以狹縫
頂點發出光波與由O 點發出的光波在P1 點的光程差為λ/2，干涉結果強度為零。同理狹縫
頂點以下第一點和O 點以下第一點的光程差也為半波長，故在P1 點其強度亦為零。如此，
兩兩相對，整個狹縫的二次子波在P1 點皆干涉為零，因此P1 點為一暗點。依此類推，P3
圖1（A） 圖1（B）
No comments:
Post a Comment