闵可夫斯基发展了庞加莱的想法,他用仿射空间来定义4维时空。如此一来,就可以在形式上用对称而统一的方式来处理时间和空间。类似于3维欧几里德空间中的坐标旋转,洛伦茨变换成为这个4维时空中的一个双曲旋转。
相对论与黎曼几何-12-双生子佯谬
|||
12. 双生子佯谬
爱因斯坦幸运地结交了两位犹太人数学家朋友:闵可夫斯基和格罗斯曼。
一开始,爱因斯坦对闵可夫斯基的四维时空不以为然,但当他结合黎曼几何考虑广义相对论的数学模型时,才认识到这个相对论少不了的数学概念的重要性。
尽管物理学家企图将时间和空间统一在一起,但两者物理意义上终有区别,无法将它们完全一视同仁,一定的场合下还必须严格加以区分。于是,天才数学家庞加莱将四维时空中的时间维和空间维分别用实数和虚数来表示。也就是说,将时空用3个实数坐标代表空间和1个虚数坐标描述时间。或者是反过来:用一个实数坐标表示时间和3个虚数坐标表示空间。到底是让空间作为实数唱主角(前者),还是像后面一种情况那样将时间表示为实数,只不过是一种约定或习惯而已。后一种表示方法是本系列文章中将经常使用的。
后来,闵可夫斯基发展了庞加莱的想法,他用仿射空间来定义4维时空。如此一来,就可以在形式上用对称而统一的方式来处理时间和空间。类似于3维欧几里德空间中的坐标旋转,洛伦茨变换成为这个4维时空中的一个双曲旋转。在欧几里德空间中,两个相邻点之间间隔的平方是一个正定二次式:
ds2 = dx2 + dy2 +dz2,
但这点不适用于闵可夫斯基时空,理由很简单,因为时空中的坐标除了实数之外,还有了虚数。根据刚才的约定,闵可夫斯基时空中两个相邻点之间间隔的平方变成了:
dt2 =dt2 - dx2 - dy2 - dz2,
这儿的dt被称为固有时。不同于欧几里德度规,闵可夫斯基时空的度规是“非正定”的。这种非正定性也导致闵氏空间具有了许多不同于欧氏空间的有趣性质。
从物理的角度,时间和空间的最根本不同是时间概念的单向性。你在空间中可以上下左右四面八方随意移动,朝一个方向前进之后可以后退再走回来。但时间却不一样了,它只能向前,不会倒流,否则便会破环因果律,产生许多不合实际情况的荒谬结论。
爱因斯坦的狭义相对论将时间和空间统一起来,彻底改变了经典的时空观,由此也产生了许多“佯谬”,双生子佯谬是其中最著名的一个。
根据相对论,对静止的观测者来说,运动物体的时钟会变慢。而相对论又认为运动是相对的。那么,有人就感到糊涂了:站在地面上的人认为火车上的人的钟更慢,坐在火车上的人认为地面上的人的钟更慢,到底是谁的钟快谁的钟慢啊?之所以问这种问题,说明人们在潜意识中仍然认为时间是“绝对”的。尽管爱因斯坦先生将同时性的概念解释得头头是道,听起来也似乎有他的道理,但是人们总觉得有问题想不通,于是,便总结出来了一个双生子佯谬。最早是由朗之万在1911年提出的。
话说地球上某年某月某日,假设在1997年吧,诞生了一对双胞胎,其中哥哥(刘天)被抱到宇宙飞船送上太空,另一人(弟弟刘地)则留守地球过普通人的日子。宇宙飞船以极快的速度(光速的四分之三)飞行。根据相对论的计算结果,在如此高的速度下,时间变慢的效应很明显,大概是3比2左右。所谓“时钟变慢”,是一种物理效应,不仅仅是时钟,而是所有与时间有关的过程,诸如植物生长、细胞分裂、原子震荡,还有你的心跳,所有的过程都放慢了脚步。总之就是说,当自认为是在“静止”参考系中的人过了3年时,运动的人却只过了2年。按照地球人的计划,1997年发射的那艘宇宙飞船,将于30年之后掉头反向以同样的速度飞回地球。因此,总共经过地球上60年之后,2057年,一对双胞胎能够再见面啦!那时候,地球上的弟弟刘地已经60岁了,但一直生活在高速运动的飞船中的哥哥刘天却只过了40个年头,人到壮年,风华正茂的年月。不过,有人便说:刘天会怎么想呢?爱因斯坦的狭义相对论不是说所有的参考系都是同等的吗?刘天在飞船中一直是静止的,地球上的弟弟却总是相对于他作高速运动,因此,他以为弟弟应该比他还年轻许多才对。但是,事实却不是这样,他看到的弟弟已经是两鬓斑白、老态初现,这便似乎构成了佯谬。无论如何,我们应该如何解释刘天心中的疑惑呢?
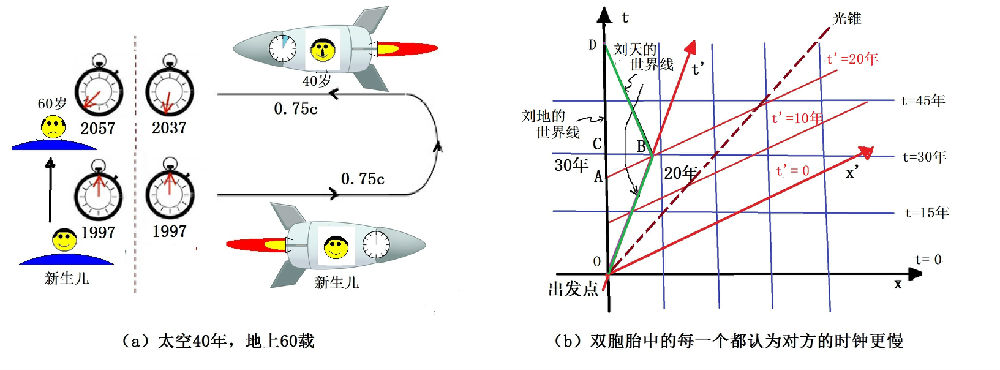
图2-12-1:双生子佯谬和同时性
首先,刘天有关狭义相对论的说法是错误的。狭义相对论并不认为所有的参考系都等同,而是认为只是惯性参考系才是等同的。刘天所在的宇宙飞船的飞行过程分成了飞离地球和飞向地球这两个阶段,每一段过程相对于地球而言都是作匀速运动,都能够分别当作是惯性参考系,但整个过程却不能在一起作为一个统一的惯性参考系。既然出发又再回头的宇宙飞船对整个过程而言并不是一个惯性参考系,刘天便不能以此而得出刘地比他年轻的结论,因而“佯谬”不成立。当刘天返回地球时,的确会发现地球上的弟弟已经比自己老了20岁。如果设想宇宙飞船的速度更快一些,快到接近光速的话,当它再次返回地球时,的确就有可能出现神话故事中描述的“山中方一日,世上已千年”的奇迹了。
我们可以使用刚才介绍的闵可夫斯基时空,更为仔细地分析这个问题。不过,我们并不需要画出4维的图形,只需要像图2-12-1b所示的,画出一个时间轴t加一个空间轴x,就足以说明问题了。
图2-12-1b中用黑线标示的直角坐标系(t,x)是地球参考系中的坐标。在这个坐标系中,两个双生子的时空过程,可以分别用他们的“世界线”来表示。什么是世界线呢?就是某个事件在时空中所走的路径。用这个新名词,以区别于仅仅是空间的“轨迹”或者仅仅时间的流逝。比如说,刘地在地球上一直没有动,所以他的世界线是沿着t轴,从出发点O->A ->C->D,图中是一条垂直向上的直线。而宇宙飞船中的刘天的世界线在图中是从O ->B ->D的一条折线。
也就是说,两个双生子的世界线都是从O到D,这是标志他们交汇见面的两个时空点:分别对应于出生时(O)和地球上60年之后(D)。两人的世界线中的一条是直线,一条是折线,这又说明什么问题呢?读者可能会认为:折线不是比直线要长吗?这点在普通空间是正确的,在“时空”中却未必见得,那是因为在这个2维时空中的距离平方:
dt2=dt2-dx2 (2-12-1)
的原因,而在普通2维坐标空间中:
ds2=dx2+dy2 (2-12-2)。
公式(2-12-1)中时空度规中的负号造成了时空空间的一些奇特性质。
首先,我们用图2-12-1b,观察解释一下时空中同时概念的相对性。对地球参考系(黑线直角坐标)而言,同时的点位于平行于x轴的同一条水平线上。比如说,地球上2012年发生的事件都在标志了“t=15年”的那条水平线上。这段时间内,宇宙飞船相对于地球作匀速运动,可以看作是一个惯性参考系。飞船参考系的坐标相对于地球参考系的坐标来说有一个旋转,如图中红色的斜线所表示。读者务必注意,这儿的所谓“坐标轴旋转”,也不同于普通空间中的旋转,被称之为“双曲旋转”,因为在闵可夫斯基时空中坐标变黄时需要保持光速不变,所以,当时间轴顺时针转动时,空间轴需要逆时针转动。在刘天的飞船参考系中看起来,平行于x’的红色斜线才是等时线。比如说,可以看看图中的A、B、C这三个事件。地球上的刘地看来,C和B是同时发生的,都发生在地球上的2027年,C点对应于自己30岁了。在宇宙飞船上的哥哥刘天呢,本来也应该是30岁,但是他的飞船时间过得慢,所以,哥哥只有20岁。飞船上的刘天怎么说呢?他不认为C和B是同时的。按照他的红线坐标,B和A才是同时的,B点对应于自己20岁,与B同时的是A点,弟弟相对于我,是运动的,时间应该更慢,所以,他还不到20岁。
在图中的这两个坐标系中(黑色和红色的),两个人的说法都是正确的,每一个人都观察到对方坐标系中的时钟比自己的更慢,从而都可以得出对方比自己更年轻的结论。但是,处于这样两个相互作匀速直线运动参考系中的双胞胎,出生且相互分离之后便永远不可能再见面,因而也就不可能构成前面所述的佯谬。不过,读者可能会说:他们虽然不能见面,但是可以通电话呀,在电话中他们互相一问,不就知道对方多少岁了么?然而,狭义相对论认为信息的速度不可能超过光速,当他们以光速通话时,也需要考虑他们之间的距离以及同时性的问题,对此我们就不进一步分析了。
在我们的故事中,地球上过了30年之后,太空船掉头向地球飞来,但这时的飞船参考系,已经不同于原来红线坐标的那一个了。要使太空船掉头达到反方向的速度,加速和减速的过程是必不可少的。在这个过程中的刘天感觉将如何?是不是被压扁或撕裂了啊?还能那么年轻力壮吗?我们且不去考虑这些种种问题,仅仅从狭义相对论时钟变慢的效应来估算他的年龄而已。
那么,既然在双生子佯谬中需要考虑宇宙飞船的加速度,是不是需要广义相对论的知识才能解释清楚它呢?也不是这样的。用地球参考系的2维时空图就可以解释清楚了。这儿,首先需要介绍一下在相对论中很重要的“固有时”概念。
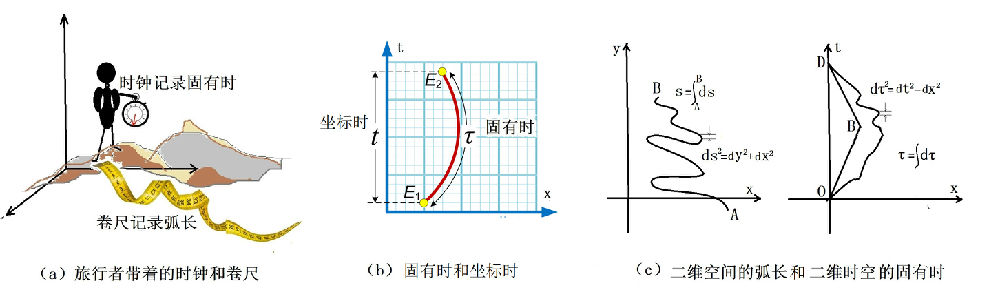
图2-12-2:固有时和坐标时的区别以及与弧长的类比
固有时,或称原时,也就是公式(2-12-1)中的t,在(2-12-1)中表示的是微分形式的dt,一段有限长度的固有时可用积分来计算得到。将公式(2-12-1)和(2-12-2)比较一下可知,固有时t类似于普通空间中弧长s的概念。在普通空间中,弧长s表示一条曲线的长度,或者说是一个人走过的路径的长度。设想如图2-12-2a的旅行者(太空人),带着自己的时钟和卷尺(计步机),一直记录他走过的距离和时间。他的计步机(或卷尺)计算测量他走过的距离,而他的时钟所记录的,就是固有时,见图2-12-2c。从图2-12-2b可以看出固有时和坐标时的区别,坐标时是事件之外的观察者使用某个参考系而记录的事件发生的时间,固有时则是旅行者自己携带的时钟记录的时间。此外,固有时与弧长不同之处是:普通空间的弧长一般比坐标数值更大,但固有时却比坐标时更小,其原因从公式(2-12-1)中显而易见,正是因为度规中空间坐标和时间坐标间的符号差。换言之,固有时用以描述时空中两个事件之间流过的时间,这个时间被赋予事件自身的时钟所测量。因而,测量结果不仅取决于两个事件对应的时空点位置,而且也取决于时钟参与其中的具体过程。再表达得更简要一点,固有时是时钟的世界线长度。
实际上,我们之前学过了黎曼几何,对固有时的概念不难理解,它就是对应于在黎曼几何中经常强调的内蕴几何不变量:弧长s。对广义相对论重要的内蕴性质,在狭义相对论中也很重要。
如何来计算两个双胞胎在重逢时各自度过的真实年龄呢?结论是:计算和比较他们在两次相遇之间的固有时。因为固有时t是内蕴不变的,这个计算可以在任何一个参考系中进行,都将得到同样的结果。每个人的年龄是由他身体的新陈代谢机制决定的,他的身体内有一个生物钟。人体处于各种运动状态(静止或运动、加速或减速)时,他的生物钟便会随着变化,或减慢,或加快,这便可以作为每个人自己带着的“时钟”。下面,我们首先用地球参考系来考察两个双胞胎在两次相遇之间的固有时。刘地一直停留在地球上没有移动,他的世界线是地球参考系中时间轴上的一段,这个参考系中,他的固有时也就等于坐标时,等于60年。而刘天的世界线是图2-12-2c右图中的OBD折线。折线中每一段的长度是20年,两段相加等于40年。所以,两个双生子在D点见面的时候,刘天40岁、刘地60岁。
从以上的分析可以体会到利用“固有时”来计算此类问题的方便之处。我们并不需要仔细考虑每个事件的过程,不需要详细去分析刘天的宇宙飞船哪一段是匀速,哪一段是加速,等等繁琐的细节,比如图2-12-2c右图中的另一条从O到D的弯弯曲曲的曲线,如果那是刘天的宇宙飞船的时空轨迹的话,只需要在地球参考系中计算这条线的固有时,那便就是刘天的年龄了。
如果不用地球参考系,使用宇宙飞船离开地球匀速运动的参考系,或者是返回时的匀速运动参考系,也都可以验证以上结果。三种情形得到同样结果:刘天40岁、刘地60岁。见图2-13-2。
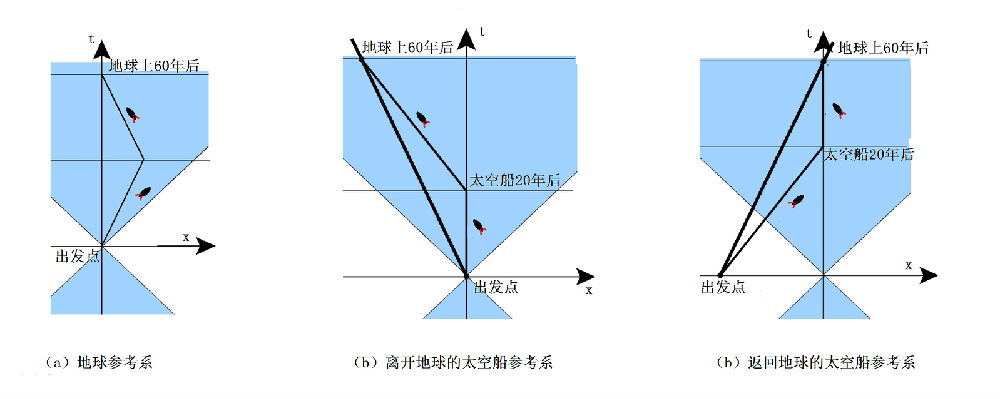
图2-12-3:使用不同的参考系计算双生子的年龄
由虚角三角函数说起,关于闵氏复时空的旋转变换
xiaojun先生在理论物理吧提出了一个问题:
http://tieba.baidu.com/f?kz=999392263
针对1.12式,xiaojun先生提出了一个问题:“式中的余弦怎么会大于1呢?”。
xiaojun认为,“如果把角度φ看做是一个虚角就正确了”
——————————————————————————————
xiaojun先生的意见是对的。即φ应该是个虚角,但是赵展岳的书中对此没有交代是说不过去的。
在φ是纯虚数的情况下,cosφ是个实数,sinφ是个纯虚数,tanφ也是个纯虚数;
而且cosφ>1其值域是大于i的实数,sinφ的值域是全体虚数,而-i<tanφ<i;
这三个虚角三角函数都不再是周期函数。
由此引出的问题是,若是复时空旋转变换,φ是虚角,那赵展岳书中的那个旋转变换的图,即图1-13是完全没有道理的!
关于复时空O(ict,x),洛仑兹变换是个旋转变换,我们能看到的教材涉及到图示,大多都是如上面图1-13的画法,也有个别教材画成O’的两个轴顺时针转动φ。
此贴下,希望能对虚角三角函数的性质引起讨论,进一步讨论闵氏复空间的旋转变换以及应该给出的正确的图示是怎样的。
http://tieba.baidu.com/f?kz=999392263
针对1.12式,xiaojun先生提出了一个问题:“式中的余弦怎么会大于1呢?”。
xiaojun认为,“如果把角度φ看做是一个虚角就正确了”
——————————————————————————————
xiaojun先生的意见是对的。即φ应该是个虚角,但是赵展岳的书中对此没有交代是说不过去的。
在φ是纯虚数的情况下,cosφ是个实数,sinφ是个纯虚数,tanφ也是个纯虚数;
而且cosφ>1其值域是大于i的实数,sinφ的值域是全体虚数,而-i<tanφ<i;
这三个虚角三角函数都不再是周期函数。
由此引出的问题是,若是复时空旋转变换,φ是虚角,那赵展岳书中的那个旋转变换的图,即图1-13是完全没有道理的!
关于复时空O(ict,x),洛仑兹变换是个旋转变换,我们能看到的教材涉及到图示,大多都是如上面图1-13的画法,也有个别教材画成O’的两个轴顺时针转动φ。
此贴下,希望能对虚角三角函数的性质引起讨论,进一步讨论闵氏复空间的旋转变换以及应该给出的正确的图示是怎样的。
上面有错误,该过来,对不起!!!
xiaojun先生的意见是对的。即φ应该是个虚角,但是赵展岳的书中对此没有交代是说不过去的。
在φ是纯虚数的情况下,cosφ是个实数,sinφ是个纯虚数,tanφ也是个纯虚数;
而且cosφ>1其值域是大于1的实数,sinφ的值域是全体虚数,而-i<tanφ<i;
这三个虚角三角函数都不再是周期函数。
xiaojun先生的意见是对的。即φ应该是个虚角,但是赵展岳的书中对此没有交代是说不过去的。
在φ是纯虚数的情况下,cosφ是个实数,sinφ是个纯虚数,tanφ也是个纯虚数;
而且cosφ>1其值域是大于1的实数,sinφ的值域是全体虚数,而-i<tanφ<i;
这三个虚角三角函数都不再是周期函数。
- 推荐 来自 贴吧游戏
教材或者本楼给出的书上的画法是如何得来的呢?
欧氏几何旋转变换大家是熟悉的,即是7楼给出的公式:
x’=xcosα+ysinα
y’=-xsinα+ycosα
而闵氏复时空的旋转变换形式是这样的:
x1=x1cosφ+x4sinφ
x4=-xsinφ+x4cosφ
其中x4=it,(采用c=1的写法)
由于这两种旋转变换有着相同的形式,所以教材给出的闵氏复时空旋转变换的图示与欧氏空间旋转变换的图示完全一样,都画成一个参考系相对另一个参考系逆时针旋转一个角。
例如这个图上的画法。

欧氏几何旋转变换大家是熟悉的,即是7楼给出的公式:
x’=xcosα+ysinα
y’=-xsinα+ycosα
而闵氏复时空的旋转变换形式是这样的:
x1=x1cosφ+x4sinφ
x4=-xsinφ+x4cosφ
其中x4=it,(采用c=1的写法)
由于这两种旋转变换有着相同的形式,所以教材给出的闵氏复时空旋转变换的图示与欧氏空间旋转变换的图示完全一样,都画成一个参考系相对另一个参考系逆时针旋转一个角。
例如这个图上的画法。

赵展岳的书上对φ没有交代,在复时空下,洛仑兹变换的复数形式是:
x1=x1cosφ+x4sinφ
x4=-xsinφ+x4cosφ
其中x4=it,(c=1),
而φ是个纯虚数!
为了引起注意,这里采用这样的写法:
x1=x1cos(iφ)+x4sin(iφ)
x4=-xsin(iφ)+x4cos(iφ)
其中φ是个实数。
既然iφ是个纯虚数,那就要看cos(iφ),sin(iφ),tan(iφ)与cos(φ),sin(φ),tan(φ)的区别是什么。
x1=x1cosφ+x4sinφ
x4=-xsinφ+x4cosφ
其中x4=it,(c=1),
而φ是个纯虚数!
为了引起注意,这里采用这样的写法:
x1=x1cos(iφ)+x4sin(iφ)
x4=-xsin(iφ)+x4cos(iφ)
其中φ是个实数。
既然iφ是个纯虚数,那就要看cos(iφ),sin(iφ),tan(iφ)与cos(φ),sin(φ),tan(φ)的区别是什么。
引入虚数纯粹是为了形式上看起来与欧氏空间相同,旋转变换画成那样也是为了与欧氏空间的旋转变换类比。我个人不太喜欢这种表达方式,闵可夫斯基空间本来就和欧氏空间不一样,没必要非要整得一样。现在比较常用的方法是认为闵可夫斯基空间的度规是g=-dx0^2+dx1^2+dx2^2+dx3^3,其中dx0=cdt,也就是说时间还是取实数,只是算距离的时候前面带上负号。用这种方法表示,前面的三角函数会变成双曲三角函数,用起来也很方便。
虚角三角函数与实角三角函数没有一一对应关系,但是与实角双曲函数却有着一一对应关系:
cos(iφ)=cosh(φ)
sin(iφ)=isinh(φ)
tan(iφ)=itan(φ)
这个结果说明,虚角三角函数和实双曲函数有着一一对应的关系。
cos(iφ)=cosh(φ)
sin(iφ)=isinh(φ)
tan(iφ)=itan(φ)
这个结果说明,虚角三角函数和实双曲函数有着一一对应的关系。
13楼:
确实写成实双曲函数的形式会带来很大的方便,但是,我认为,若是追求数学上的严密性,双曲函数形式的洛仑兹变换也是不严格的。
为什么呢?因为时空间隔一般是用s²的来表示的,若是我们定义s是间隔的线长,即一条几何意义上的长度,那s就会出现虚数。而在实时空上O(t,x)出现虚数是很尴尬的事情。而在复时空O(it,x)上,s为虚数是很自然的事情,虚数表示这个几何线条是个类时间隔的线长。
所以,虚角三角函数或者称为虚参数三角函数形式的洛仑兹变换比实参数双曲函数来的更严格。
确实写成实双曲函数的形式会带来很大的方便,但是,我认为,若是追求数学上的严密性,双曲函数形式的洛仑兹变换也是不严格的。
为什么呢?因为时空间隔一般是用s²的来表示的,若是我们定义s是间隔的线长,即一条几何意义上的长度,那s就会出现虚数。而在实时空上O(t,x)出现虚数是很尴尬的事情。而在复时空O(it,x)上,s为虚数是很自然的事情,虚数表示这个几何线条是个类时间隔的线长。
所以,虚角三角函数或者称为虚参数三角函数形式的洛仑兹变换比实参数双曲函数来的更严格。
其实,深入讨论闵氏复时空的旋转变换,会得到十分严密的结果。也就明白为何一般定义时空间隔采用s²而不直接定义s。有了ict,会带来额外的好处,那就是闵氏时空下任何一条几何意义的曲线可以进行线积分。
若不是这样,对线积分时,要处理虚数,引起数学上的麻烦。当然,物理不是数学,一般也似乎无需较真。
但是,若是较真,例如上面给出的复时空的旋转变换的图示,就可以看出那个图是完全没有道理的。不从数学上说,仅仅从物理上说就是错误的!
若不是这样,对线积分时,要处理虚数,引起数学上的麻烦。当然,物理不是数学,一般也似乎无需较真。
但是,若是较真,例如上面给出的复时空的旋转变换的图示,就可以看出那个图是完全没有道理的。不从数学上说,仅仅从物理上说就是错误的!
12楼带撇的量,忘记写撇了,对不起,应该是:
赵展岳的书上对φ没有交代,在复时空下,洛仑兹变换的复数形式是:
x'1=x1cosφ+x4sinφ
x'4=-xsinφ+x4cosφ
其中x4=it,(c=1),
而φ是个纯虚数!
为了引起注意,这里采用这样的写法:
x'1=x1cos(iφ)+x4sin(iφ)
x'4=-xsin(iφ)+x4cos(iφ)
其中φ是个实数。
既然iφ是个纯虚数,那就要看cos(iφ),sin(iφ),tan(iφ)与cos(φ),sin(φ),tan(φ)的区别是什么。
赵展岳的书上对φ没有交代,在复时空下,洛仑兹变换的复数形式是:
x'1=x1cosφ+x4sinφ
x'4=-xsinφ+x4cosφ
其中x4=it,(c=1),
而φ是个纯虚数!
为了引起注意,这里采用这样的写法:
x'1=x1cos(iφ)+x4sin(iφ)
x'4=-xsin(iφ)+x4cos(iφ)
其中φ是个实数。
既然iφ是个纯虚数,那就要看cos(iφ),sin(iφ),tan(iφ)与cos(φ),sin(φ),tan(φ)的区别是什么。
为什么说这个图上复时空的旋转变换在物理上就是错的呢:
因为:
x'1=x1cosφ+x4sinφ
x'4=-xsinφ+x4cosφ
其中x4=it,(c=1)
这个式子表示的是带撇的参考系是向x正方向运动的参考系,也就是说,x'4轴即it轴应该是顺时针旋转,而绝不可能逆时针旋转。这从物理意义上完全不对!!!
不仅如此,从数学上说,我们按照“描点”做图,给出实际数值在x1,x4坐标下画出x'1,和x'4,那x'4也一定是顺时针转,而不会逆时针转!!!

因为:
x'1=x1cosφ+x4sinφ
x'4=-xsinφ+x4cosφ
其中x4=it,(c=1)
这个式子表示的是带撇的参考系是向x正方向运动的参考系,也就是说,x'4轴即it轴应该是顺时针旋转,而绝不可能逆时针旋转。这从物理意义上完全不对!!!
不仅如此,从数学上说,我们按照“描点”做图,给出实际数值在x1,x4坐标下画出x'1,和x'4,那x'4也一定是顺时针转,而不会逆时针转!!!

你不要想着把它去开个方。如果你学过线性代数,你应该知道,代数中对度规的描述其实是一个对称双线性型。欧氏度规是正定的,所以可以开方,闵可夫斯基空间的度规不是正定的,不可以开方也完全没必要开方。复时空好像坐标都取的复数,它似乎应该是C^4。但它有几个限制,类空坐标必须是实数,类时坐标必须是纯虚数,并且如果一个数要与一个向量做数乘,这个数必须是实数。所以从它的线性结构来说是与R^4完全一样的。所以从代数上来说一般就当成R^4,而不会用一个坐标是虚数三个坐标是实数这种怪异结构。特别是到广义相对论,完全是用伪黎曼流形的理论来处理,这种虚数表达法就更显得无力。

还有,如果要用虚数,你就不要老去想那个图,一个C^2的图根本不可能画在一个平面内,而且如果用了复数,什么叫夹角也显得很不明确。这个还是要完全从代数的角度推出变换的表达式。
这时候我觉得时间用实数反而更好一些,你也画一个图,就会发现空间轴逆时针旋转的时候时间轴会顺时针旋转。可能你会觉得为什么新的空间轴和时间轴不垂直,其实在闵可夫斯基度规下它们就是垂直的。
这时候我觉得时间用实数反而更好一些,你也画一个图,就会发现空间轴逆时针旋转的时候时间轴会顺时针旋转。可能你会觉得为什么新的空间轴和时间轴不垂直,其实在闵可夫斯基度规下它们就是垂直的。
什么叫夹角也显得很不明确。这个还是要完全从代数的角度推出变换的表达式。
+++++++++++++++++++++++++++++
夹角的几何意义十分明确,虚角是用对应的单位双曲线的间隔线长来定义的!
这和实角三角函数的角度用弧度来定义有着一样的几何意义!!!
这个正在写一骗文章,专门讨论这个夹角的几何意义和物理意义。
+++++++++++++++++++++++++++++
夹角的几何意义十分明确,虚角是用对应的单位双曲线的间隔线长来定义的!
这和实角三角函数的角度用弧度来定义有着一样的几何意义!!!
这个正在写一骗文章,专门讨论这个夹角的几何意义和物理意义。
例如我们知道闵氏时空上,匀加速(四加速)粒子的世界线点是双曲线,这个双曲线是粒子的世界线,所以其线长应该是个类时间隔,即积出的结果应该是一个虚数。这个虚数的间隔线长s就是粒子的原时!即it的值。
而这个it即粒子的原时就是虚角三角函数的角度和双曲线到时空原点的间隔线长的乘积。
这和欧氏几何下,弧长的积分有着一样的结果。
这个我曾在本论坛给出过结果,但是是用双曲函数给出的,避免了虚数的出现。但是显然是不严格的。还是虚角三角函数可以给出严格的结果。
而这个it即粒子的原时就是虚角三角函数的角度和双曲线到时空原点的间隔线长的乘积。
这和欧氏几何下,弧长的积分有着一样的结果。
这个我曾在本论坛给出过结果,但是是用双曲函数给出的,避免了虚数的出现。但是显然是不严格的。还是虚角三角函数可以给出严格的结果。


25楼:不管你怎样运用几何,总之都是一句话:因为闵氏时空度规并不是正定的,所以你想用空间旋转的方式做到完全准确的表达洛仑兹变换,那是不可能的。
+++++++++++++++++++++++++++++++++
是不是能准确地反映洛仑兹变换正是这个帖子要讨论的问题。
先把这个虚角的几何意义给出,给一个单位旋转的实例。
我们由此可以看出,在欧氏几何下iφ的几何意义确实很难定义。
但是在闵氏几何下,这个iφ的几何意义是很明确的!!请看这个图,以x轴的旋转为例:

+++++++++++++++++++++++++++++++++
是不是能准确地反映洛仑兹变换正是这个帖子要讨论的问题。
先把这个虚角的几何意义给出,给一个单位旋转的实例。
我们由此可以看出,在欧氏几何下iφ的几何意义确实很难定义。
但是在闵氏几何下,这个iφ的几何意义是很明确的!!请看这个图,以x轴的旋转为例:

这本书我很早以前读过,我想它只是作为一本尽量直观和简单的入门书,所以之所以那样画变换图,也许只能认为是一种比喻,是考虑到读者群而取的权宜之计,想说明的只是这样一点:把二维空间保欧式度规的正交变换取虚角(延拓到虚轴上),则得到我们要的保闵氏度规的洛伦兹变换。

上面的例子说明,闵氏时空下,特别是复闵氏时空下,虚参数三角函数的几何意义和洛仑兹变换是严丝合缝!
例如,cosiφ是个实数,而cosiφ=γ,显然应该是实数!
而且在闵氏时空上,cosiφ要么是类空间隔和类空间隔的比,要么是类时间隔和类时间隔的比,所以一定是实数。不仅如此,cosiφ还是大等于1的正实数,这正和洛仑兹变换相符!
siniφ是个纯虚数,在闵氏时空上正是类时与类空的比,或者类空与类时的比,所以一定是个虚数!
例如,cosiφ是个实数,而cosiφ=γ,显然应该是实数!
而且在闵氏时空上,cosiφ要么是类空间隔和类空间隔的比,要么是类时间隔和类时间隔的比,所以一定是实数。不仅如此,cosiφ还是大等于1的正实数,这正和洛仑兹变换相符!
siniφ是个纯虚数,在闵氏时空上正是类时与类空的比,或者类空与类时的比,所以一定是个虚数!
回复:讨论::由虚角三角函数说起,关于闵氏复时空的旋转变换
这不是钻牛角尖,所有的关系要用数学来说话。若数学的结果与物理意义有冲突,那肯定是不行的。
例如我说教材的那个画法不对,至少在物理意义上是不对的!it轴要顺时针转(对应于洛仑兹正变换),而不能逆时针转!因为逆时针转就表明带撇的参考系沿着x的负方向运动了!与正变换的约定不一致!!!这应该是起码的常识!
例如我说教材的那个画法不对,至少在物理意义上是不对的!it轴要顺时针转(对应于洛仑兹正变换),而不能逆时针转!因为逆时针转就表明带撇的参考系沿着x的负方向运动了!与正变换的约定不一致!!!这应该是起码的常识!
虚角三角函数完全符合闵氏度规的定义:
这个式子就是二维复空间度规的等价表示cos²(iφ)+sin²(iφ)=1
若cos( iφ)>∣sin( iφ)∣则为类空间隔
cos( iφ)<∣sin( iφ)∣,则为类时间隔
(注:cosiφ是大于等于1的实数)
这个式子就是二维复空间度规的等价表示cos²(iφ)+sin²(iφ)=1
若cos( iφ)>∣sin( iφ)∣则为类空间隔
cos( iφ)<∣sin( iφ)∣,则为类时间隔
(注:cosiφ是大于等于1的实数)
采用虚参数三角函数能够准确诠释洛仑兹变换,还有一个令人十分兴奋的结果:
这就是,若旋转角iφ的φ趋于无穷的的话,x轴与it轴都将趋于光的世界线!!!
也就是,若φ趋于无穷大,tan(iφ)趋于i,即:∣tan( iφ)∣趋于1,即光速c!
这也说明复空间的旋转变换的校准线是双曲线,光就是双曲线的渐近线!!!
这正是洛仑兹旋转变换的本意!!得到这个结果你不感到荡气回肠吗?
这就是,若旋转角iφ的φ趋于无穷的的话,x轴与it轴都将趋于光的世界线!!!
也就是,若φ趋于无穷大,tan(iφ)趋于i,即:∣tan( iφ)∣趋于1,即光速c!
这也说明复空间的旋转变换的校准线是双曲线,光就是双曲线的渐近线!!!
这正是洛仑兹旋转变换的本意!!得到这个结果你不感到荡气回肠吗?
从数学上说:
虚参数三角函数和实参数双曲函数有着对应关系,即虚参数三角函数可以和双曲线对应起来;
而虚参数双曲函数和实角三角函数有着对应关系,即虚参数双曲函数可以和园对应起来。
若是洛仑兹变换可以写成虚参数双曲函数,那洛仑兹变换就可以是园旋转不变的,可惜不能!
但是恰恰洛仑兹变换可以写成虚参数三角函数,所以,洛仑兹变换是双曲旋转不变的,无论是写成实形式还是复形式!
虚参数三角函数和实参数双曲函数有着对应关系,即虚参数三角函数可以和双曲线对应起来;
而虚参数双曲函数和实角三角函数有着对应关系,即虚参数双曲函数可以和园对应起来。
若是洛仑兹变换可以写成虚参数双曲函数,那洛仑兹变换就可以是园旋转不变的,可惜不能!
但是恰恰洛仑兹变换可以写成虚参数三角函数,所以,洛仑兹变换是双曲旋转不变的,无论是写成实形式还是复形式!
前面有朋友说,复时空下的旋转角的几何意义不明显。这句话显然是结论下得早了点。
其实闵氏复时空下旋转变换的旋转虚角度,其几何意义是十分明显和确定的。除了前面给出的具体例子,这个虚角度可以由正交的三角形的变长(由间隔来度量,要区分类时与类空)来定义,而且,这个虚角实际也是一种“弧度”,即用单位双曲线的线长s来度量。这与欧氏几何下的单位园的弧长与角度的对应关系完全一样。
下面就给出这个证明。
我们用了一个单位双曲线来考察这个问题,当然对于一般结果也是对的。这个结果还有一个意义,就是可以对匀加速粒子的世界线积分,即求得它的原时。这个原时是类时间隔的线长,所以积出的结果应该是一个虚数。

其实闵氏复时空下旋转变换的旋转虚角度,其几何意义是十分明显和确定的。除了前面给出的具体例子,这个虚角度可以由正交的三角形的变长(由间隔来度量,要区分类时与类空)来定义,而且,这个虚角实际也是一种“弧度”,即用单位双曲线的线长s来度量。这与欧氏几何下的单位园的弧长与角度的对应关系完全一样。
下面就给出这个证明。
我们用了一个单位双曲线来考察这个问题,当然对于一般结果也是对的。这个结果还有一个意义,就是可以对匀加速粒子的世界线积分,即求得它的原时。这个原时是类时间隔的线长,所以积出的结果应该是一个虚数。

35楼给出it轴的旋转时,将虚角改成负的虚角,显然这是恒等变换。没有什么不同。
当然你也可以写成正的虚角的形式,例如一般教材给出的那样,例如这样写:
x'1=x1cos(iφ)+x4sin(iφ)
x4=it,c=1
即便是写成这种形式,可以具体代入数值,采用描点画图法,画出it'轴,结果是一样的!有兴趣的朋友不妨试试。
但是it'轴的旋转写成负虚数的形式更能体现其几何意义,这个对照前面给出的图,我想朋友们会自己得出结论。
当然你也可以写成正的虚角的形式,例如一般教材给出的那样,例如这样写:
x'1=x1cos(iφ)+x4sin(iφ)
x4=it,c=1
即便是写成这种形式,可以具体代入数值,采用描点画图法,画出it'轴,结果是一样的!有兴趣的朋友不妨试试。
但是it'轴的旋转写成负虚数的形式更能体现其几何意义,这个对照前面给出的图,我想朋友们会自己得出结论。
顺便在这个帖子下对坂上中微子先生在理论物理吧的以下观点提出不同意见:
坂上中微子认为:
“
但是时间和空间的属性毕竟是完全不同的,怎么办呢?闵可夫斯基很聪明,他在ct前乘上了一个虚数单位i,变成了复四维时空,以此来表明,时间和空间仍然是不同的!然后,大家在这个基础上又引入了一系列四维量,魔术似乎就变得成功了。
但是这为什么只是个魔术呢?因为这种处理方法并没有体现时间的本质。试想,如果我不让ct与i相乘,而改用空间坐标x,y,z与i相乘,变成(ix,iy,iz,ct),这套坐标不是一样能描述四维运动吗?显然能,而且功能与闵氏复四维时空完全相同,但这里却变成了时间可逆,空间反倒变得不可逆了,这干脆就不符合观测事实,显然是荒谬的,所以复四维时空的荒谬之处就显现出来了。
”
通过上面我们讨论复时空的旋转变换,可以看出坂上中微子先生的以上议论是毫无道理的。复四维也好,实四维也好,没有什么不同!复四维只是一种数学技巧,而且复四维时空的表达能够更严格地讨论四维间隔这个概念,与时间是不是可逆没有任何关系!!!
坂上中微子认为:
“
但是时间和空间的属性毕竟是完全不同的,怎么办呢?闵可夫斯基很聪明,他在ct前乘上了一个虚数单位i,变成了复四维时空,以此来表明,时间和空间仍然是不同的!然后,大家在这个基础上又引入了一系列四维量,魔术似乎就变得成功了。
但是这为什么只是个魔术呢?因为这种处理方法并没有体现时间的本质。试想,如果我不让ct与i相乘,而改用空间坐标x,y,z与i相乘,变成(ix,iy,iz,ct),这套坐标不是一样能描述四维运动吗?显然能,而且功能与闵氏复四维时空完全相同,但这里却变成了时间可逆,空间反倒变得不可逆了,这干脆就不符合观测事实,显然是荒谬的,所以复四维时空的荒谬之处就显现出来了。
”
通过上面我们讨论复时空的旋转变换,可以看出坂上中微子先生的以上议论是毫无道理的。复四维也好,实四维也好,没有什么不同!复四维只是一种数学技巧,而且复四维时空的表达能够更严格地讨论四维间隔这个概念,与时间是不是可逆没有任何关系!!!
两种数学上完全等价的描述,哪有什么谁更严格的问题。
++++++++++++++++++++++++++++++++
嗯,至少能承认是等价的描述,那就是说,实数形式与复数形式的数学表达是等效的。即,意味着既然实时空是双曲旋转不变的,那复时空就也是双曲旋转不变的。也就是说,顶楼给出的书上给出的图示是错的。是不是呢?
更严格是指的复时空可以完全放心的对线,直线和曲线进行积分,类时的积出个虚数,类空积出个实数。
在实时空,会出现线积分为虚数,不是很不严格吗?
++++++++++++++++++++++++++++++++
嗯,至少能承认是等价的描述,那就是说,实数形式与复数形式的数学表达是等效的。即,意味着既然实时空是双曲旋转不变的,那复时空就也是双曲旋转不变的。也就是说,顶楼给出的书上给出的图示是错的。是不是呢?
更严格是指的复时空可以完全放心的对线,直线和曲线进行积分,类时的积出个虚数,类空积出个实数。
在实时空,会出现线积分为虚数,不是很不严格吗?
虽然是坟,但确实忍不住说几句。所谓虚参数三角函数在这里根本就没有任何必要。如果你的数学足够好,你应该会知道Lorentz群和正交几何。Lorentz变换不过是一般正交几何里面的一个特殊的小问题而已,有双曲函数的表示方法也完全不奇怪。总合起来,还是数学学得太少。
这是一个坟贴,被顶起来了。11年我贴出这个帖子时,赞成者不多,批评者不少。3年多过去了,再看到这个帖子,还是有颇多的感触。
本吧有很多屋里专业的学生和先进者,对于主流教科书中的批评,往往不大能得到鼓励与支持。有朋友往往会凭着本能对批评者的意见给予反驳。但是,这些朋友也许并没有认真的读一读批评者的意见。
洛伦兹变换是一种非欧几何下的“特殊”的旋转变换,可以用双曲函数来描述,也可以用虚角三角函数来表述。
这个并不是我的发明,在权威的著作中,就有用双曲函数或虚角三角函数来讨论洛伦兹变换的。例如刘辽的《狭义相对论》第二版。
下面的图就是刘辽《狭义相对论》第二版中的相关页面:

刘辽教授这一节的解析论述是不错的,但是此页图13.1(b)复闵氏空间的旋转变换却是没有道理的!或者说是完全错误的!
这一错误,也反映在本贴提到的赵展岳的《相对论导引》一书中。
本人作为爱好者,或者说是“民科”在我的一本无知无畏的作品《闵氏几何与狭义相对论》中,对这个问题做了详细的讨论,并对权威意见提出了批评。
我的这种批评当然欢迎得到反批评,好在我没有什么负担,一个爱好者而已。
本吧有很多屋里专业的学生和先进者,对于主流教科书中的批评,往往不大能得到鼓励与支持。有朋友往往会凭着本能对批评者的意见给予反驳。但是,这些朋友也许并没有认真的读一读批评者的意见。
洛伦兹变换是一种非欧几何下的“特殊”的旋转变换,可以用双曲函数来描述,也可以用虚角三角函数来表述。
这个并不是我的发明,在权威的著作中,就有用双曲函数或虚角三角函数来讨论洛伦兹变换的。例如刘辽的《狭义相对论》第二版。
下面的图就是刘辽《狭义相对论》第二版中的相关页面:

刘辽教授这一节的解析论述是不错的,但是此页图13.1(b)复闵氏空间的旋转变换却是没有道理的!或者说是完全错误的!
这一错误,也反映在本贴提到的赵展岳的《相对论导引》一书中。
本人作为爱好者,或者说是“民科”在我的一本无知无畏的作品《闵氏几何与狭义相对论》中,对这个问题做了详细的讨论,并对权威意见提出了批评。
我的这种批评当然欢迎得到反批评,好在我没有什么负担,一个爱好者而已。












No comments:
Post a Comment