[代數拓樸]基本群
In 拓樸學 on 05/23/2012 at 8:56 下午
假設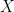 是一個拓樸空間。連續函數
是一個拓樸空間。連續函數![c:[0,1]\to X c:[0,1]\to X](https://s0.wp.com/latex.php?latex=c%3A%5B0%2C1%5D%5Cto+X&bg=FFFFFF&fg=000000&s=0) 稱為
稱為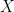 上的一條曲線(或路徑)。如果
上的一條曲線(或路徑)。如果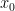 是
是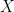 上的一點。任何起點跟終點都在
上的一點。任何起點跟終點都在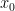 的路徑都叫做迴圈(loop),換句話說,曲線
的路徑都叫做迴圈(loop),換句話說,曲線![c:[0,1]\to X c:[0,1]\to X](https://s0.wp.com/latex.php?latex=c%3A%5B0%2C1%5D%5Cto+X&bg=FFFFFF&fg=000000&s=0) 是一個通過
是一個通過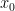 的迴圈的充要條件是
的迴圈的充要條件是 如圖所示:
如圖所示:
![[c]\cdot[d]=[c*d]. [c]\cdot[d]=[c*d].](https://s0.wp.com/latex.php?latex=%5Bc%5D%5Ccdot%5Bd%5D%3D%5Bc%2Ad%5D.&bg=FFFFFF&fg=000000&s=0)

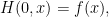
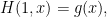
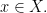
![\pi_{1}(f)[c]=[f\circ c]. \pi_{1}(f)[c]=[f\circ c].](https://s0.wp.com/latex.php?latex=%5Cpi_%7B1%7D%28f%29%5Bc%5D%3D%5Bf%5Ccirc+c%5D.&bg=FFFFFF&fg=000000&s=0)

![\displaystyle\pi_{1}(S)=\langle a_{1},b_{1},\cdots,a_{g},b_{g}|\prod_{i=1}^{g}[a_{i},b_{i}]=1\rangle. \displaystyle\pi_{1}(S)=\langle a_{1},b_{1},\cdots,a_{g},b_{g}|\prod_{i=1}^{g}[a_{i},b_{i}]=1\rangle.](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle%5Cpi_%7B1%7D%28S%29%3D%5Clangle+a_%7B1%7D%2Cb_%7B1%7D%2C%5Ccdots%2Ca_%7Bg%7D%2Cb_%7Bg%7D%7C%5Cprod_%7Bi%3D1%7D%5E%7Bg%7D%5Ba_%7Bi%7D%2Cb_%7Bi%7D%5D%3D1%5Crangle.&bg=FFFFFF&fg=000000&s=0)
如果![c:[0,1]\to X c:[0,1]\to X](https://s0.wp.com/latex.php?latex=c%3A%5B0%2C1%5D%5Cto+X&bg=FFFFFF&fg=000000&s=0) 與
與![d:[0,1]\to X d:[0,1]\to X](https://s0.wp.com/latex.php?latex=d%3A%5B0%2C1%5D%5Cto+X&bg=FFFFFF&fg=000000&s=0) 是兩條
是兩條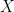 上的曲線,並且
上的曲線,並且 我們可以把這兩條曲線給接合起來,新的曲線就稱為
我們可以把這兩條曲線給接合起來,新的曲線就稱為 的接合曲線,並記為
的接合曲線,並記為 為了讓
為了讓 的定義域是
的定義域是![[0,1] [0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=FFFFFF&fg=000000&s=0) ,我們令:當
,我們令:當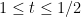 時,
時,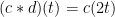 且
且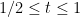 時,
時,
如果![c:[0,1]\to X c:[0,1]\to X](https://s0.wp.com/latex.php?latex=c%3A%5B0%2C1%5D%5Cto+X&bg=FFFFFF&fg=000000&s=0) 是一條曲線,我們可以定義這條曲線的逆曲線
是一條曲線,我們可以定義這條曲線的逆曲線 如下。
如下。![(-c):[0,1]\to X, (-c):[0,1]\to X,](https://s0.wp.com/latex.php?latex=%28-c%29%3A%5B0%2C1%5D%5Cto+X%2C&bg=FFFFFF&fg=000000&s=0) 定義為
定義為 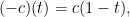
 。換句話說,新曲線的起點為原曲線的終點,新曲線的終點為原曲線的起點。(想成運動路徑的話,就是沿著原來的路徑逆向跑回去原點)
。換句話說,新曲線的起點為原曲線的終點,新曲線的終點為原曲線的起點。(想成運動路徑的話,就是沿著原來的路徑逆向跑回去原點)
假設![c,d:[0,1]\to X c,d:[0,1]\to X](https://s0.wp.com/latex.php?latex=c%2Cd%3A%5B0%2C1%5D%5Cto+X&bg=FFFFFF&fg=000000&s=0) 是
是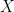 上的兩條曲線,並且
上的兩條曲線,並且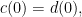
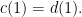 如果
如果 可以透過連續變形(continuous deformation)的方式變成曲線
可以透過連續變形(continuous deformation)的方式變成曲線 則我們稱曲線
則我們稱曲線 (固定端點式)同倫於(homotopic)曲線
(固定端點式)同倫於(homotopic)曲線 並且記為
並且記為
固定觀點的同倫的數學定義如下。如果存在連續映射![F:[0,1]\times [0,1]\to X F:[0,1]\times [0,1]\to X](https://s0.wp.com/latex.php?latex=F%3A%5B0%2C1%5D%5Ctimes+%5B0%2C1%5D%5Cto+X&bg=FFFFFF&fg=000000&s=0) 使得
使得
(1) 且
且

(2) 且
且
我們稱 同倫於
同倫於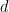 。而我們稱連續函數族
。而我們稱連續函數族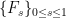 是從
是從 形變至
形變至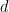 的同倫。
的同倫。
我們定義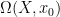 為所有通過
為所有通過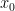 的迴圈所成的集合。則我們可以驗證同倫
的迴圈所成的集合。則我們可以驗證同倫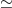 在
在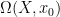 上定義出一個等價關係
上定義出一個等價關係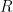 ,如果
,如果 是一個迴圈,我們記
是一個迴圈,我們記![[c] [c]](https://s0.wp.com/latex.php?latex=%5Bc%5D&bg=FFFFFF&fg=000000&s=0) 為
為 的等價類(equivalent class)。這個等價關係所構成的商集合
的等價類(equivalent class)。這個等價關係所構成的商集合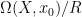 記為
記為 我們可以在這個商集合上面定義一個運算
我們可以在這個商集合上面定義一個運算 如下:
如下:
則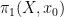 構成一個群,稱為
構成一個群,稱為 的基本群(fundamental group)。其單位元定義如下。令
的基本群(fundamental group)。其單位元定義如下。令 為常數映射,則
為常數映射,則![[e_{x_{0}}] [e_{x_{0}}]](https://s0.wp.com/latex.php?latex=%5Be_%7Bx_%7B0%7D%7D%5D&bg=FFFFFF&fg=000000&s=0) 是基本群的單位元。如果
是基本群的單位元。如果![[c] [c]](https://s0.wp.com/latex.php?latex=%5Bc%5D&bg=FFFFFF&fg=000000&s=0) 是基本群的一個元素,則
是基本群的一個元素,則![[c]^{-1}=[-c]. [c]^{-1}=[-c].](https://s0.wp.com/latex.php?latex=%5Bc%5D%5E%7B-1%7D%3D%5B-c%5D.&bg=FFFFFF&fg=000000&s=0) 如果
如果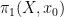 與選取的
與選取的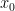 無關,則我們記
無關,則我們記
範例1. 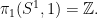
這個證明會等到我引入拓樸空間的universal cover時會介紹。
範例2. 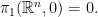
證明:假設![c:[0,1]\to \mathbb{R}^{n} c:[0,1]\to \mathbb{R}^{n}](https://s0.wp.com/latex.php?latex=c%3A%5B0%2C1%5D%5Cto+%5Cmathbb%7BR%7D%5E%7Bn%7D&bg=FFFFFF&fg=000000&s=0) 通過原點的一個迴圈。定義
通過原點的一個迴圈。定義
![(s,t)\in [0,1]^{2}. (s,t)\in [0,1]^{2}.](https://s0.wp.com/latex.php?latex=%28s%2Ct%29%5Cin+%5B0%2C1%5D%5E%7B2%7D.&bg=FFFFFF&fg=000000&s=0) 則
則 定義出從
定義出從 到
到 的同倫。因此,任何的迴圈都同倫於常數迴圈。所以
的同倫。因此,任何的迴圈都同倫於常數迴圈。所以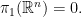
定理:假設 與
與 是兩個具有基點(base point)的拓樸空間。則
是兩個具有基點(base point)的拓樸空間。則
利用上述定理可以立即推出:
範例3. 令 表示輪胎面,則
表示輪胎面,則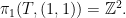
如果兩個連續映射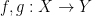 滿足下列關係,則我們稱
滿足下列關係,則我們稱 是同倫的:
是同倫的:
假設存在一連續映射![H:[0,1]\times X\to Y H:[0,1]\times X\to Y](https://s0.wp.com/latex.php?latex=H%3A%5B0%2C1%5D%5Ctimes+X%5Cto+Y&bg=FFFFFF&fg=000000&s=0) 使得
使得
如果 同倫,我們記
同倫,我們記 如果
如果 與
與 是連續映射,並且
是連續映射,並且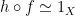 且
且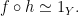 則我們稱
則我們稱 是同倫等價。
是同倫等價。
定理:如果拓樸空間 與拓樸空間
與拓樸空間 是同倫等價的(homotopy equivalent),則
是同倫等價的(homotopy equivalent),則
利用這個定理我們可以推論出,兩個同胚的拓樸空間他們具有相同的基本群。換句話說,基本群是拓樸不變量(topological invariant)。
定理:如果 是一個連續映射,我們定義
是一個連續映射,我們定義
則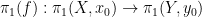 是一個群同態(group homomorphism)。
是一個群同態(group homomorphism)。
令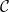 表示所有由具有基點的拓樸空間所成的範疇,並且
表示所有由具有基點的拓樸空間所成的範疇,並且 是所有群所成的範疇。利用上述定理我們可以得到
是所有群所成的範疇。利用上述定理我們可以得到
是一個從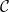 映至
映至 的函子(functor)。
的函子(functor)。
範例4.令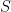 表示一個緊緻可定向的曲面。則存在
表示一個緊緻可定向的曲面。則存在 中的元素
中的元素 使得
使得 是
是 中滿足關係
中滿足關係 的一組生成元。而
的一組生成元。而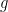 決定於
決定於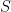 的拓樸,稱為
的拓樸,稱為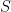 的虧格數(genus)。如果以群論的寫法,我們可以寫
的虧格數(genus)。如果以群論的寫法,我們可以寫
其中![[a,b]=aba^{-1}b^{-1} [a,b]=aba^{-1}b^{-1}](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D%3Daba%5E%7B-1%7Db%5E%7B-1%7D&bg=FFFFFF&fg=000000&s=0) 是
是 的對易子(commutator)。
的對易子(commutator)。
本圖為虧格數為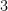 的緊緻可定向曲面。
的緊緻可定向曲面。
本圖虧格數為 的緊緻可定向曲面(也就是輪胎面)。
的緊緻可定向曲面(也就是輪胎面)。
我們可以取迴圈 如上圖。而
如上圖。而![[a,b]=1 [a,b]=1](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D%3D1&bg=FFFFFF&fg=000000&s=0) 等價於
等價於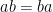 。換句話說,利用這個關係可以知道
。換句話說,利用這個關係可以知道 是一個交換群,並且
是一個交換群,並且 是一組生成元。那麼我們可以知道
是一組生成元。那麼我們可以知道 是由
是由 生成的自由交換群(free abelian group),也就是說
生成的自由交換群(free abelian group),也就是說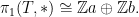 跟我們先前得到的結果相符合。
跟我們先前得到的結果相符合。
附註:拓樸不變量的定義是:給定某個代數量,如果他在同胚映射的作用下不變,那麼,我們就稱他是一個拓樸不變量。






No comments:
Post a Comment