ir.lib.bnu.edu.cn/irp/item.do?handle=123456789/141880
轉為繁體網頁
第六节是对端点固定变分的变分矢量场的“加速度”（横向加速度）的讨论，由于由类光最长线 - 北京师范大学机构库- 检索结果
ir.lib.bnu.edu.cn/irp/search.do?q=(keyword...
轉為繁體網頁
第六节是对端点固定变分的变分矢量场的“加速度”（横向加速度）的讨论，由于由类光[PDF]黑洞与时间的性质
www.cs.wichita.edu/~chou/jian/chou2/BlackHole1.pdf
2015年6月4日 - 这时，类时测地线不是类光测地线变分出来的，也就是. 说，无共辄点的情况，变分参量肯定会随仿射参量增加而增加，这可以从公式中. 看到，即比较 ...变分法建模
· 1 变分法简介 · 2 应用
问题一： 等周问题（古希腊） 1：给定一平面封闭曲线 Γ ，使得所围的平面图形面积最大。 2：延拓到多维时的情形。
空间曲面面积的定义：曲面微元向切平面作投影的微元面积， 作和，求极限
8：变分建模法
变分法建模
· 1 变分法简介 · 2 应用
问题一： 等周问题（古希腊） 1：给定一平面封闭曲线 Γ ，使得所围的平面图形面积最大。 2：延拓到多维时的情形。
Γ
空间曲面面积的定义：曲面微元向切平面作投影的微元面积， 作和，求极限。 以3维空间为例z=z(x,y),
z |·· =Γ = zΓ
s = min ∫∫ 1 + z + z dxdy
2 x 2 y ·
z |·· =Γ = zΓ
二：Euclid问题 A B
水平镜面 选择P点，使得AP+PB最短
推广的问题，折射。 三： 捷线问题（John.Berluli） A
B 找一条从A到B的连续曲线，当小球只受重力作用， 从A到B的时间最短 1 2 mv = mgy, v = 2 gy 2 等时线，旋轮线 ds
ds = (dx) 2 + (dy ) 2 , dt = v
B xB
( xB , y B )
ds T =∫ = v A
∫
0
1 + y '2 2 gy
dx
四： 最短路问题 A(x1,y1)
y(x) B(x2,y2) 求连接AB的最短线。
L = ∫ 1 + y ' dx
2
1: 平面 2：球面
直线 测地线
变分法简介： 变分法简介：
变分法基本概念 1：变分 设S为一函数集，若对于每一个S中的函数x(t)有一个实数 J与之对应，则称J是定义在S上的泛函 记作J(x(t)),S称为容许函数集
对于平面 xy上过定点 A（x 1 , y 1）和B（x 2 , y 2）的每一条光滑曲线 y ( x )， 绕x轴旋转得到一个旋转体 ，如图，旋转体的侧面 积是曲 如图， 线y ( x )的泛函由微分知识有
x2
s=
∫
2πy ( x ) (1 + y' 2 ( x ))dx
x1
容许函数集为 S = {y(x) | y(x) ∈ C 1 [x 1 , x 2 ], y ( x 1 ) = y 1 , y ( x 2 ) = y 2 } ( 2)
最简泛函的形式：
t2
J ( x(t )) = F(t , x, x' )dt
t1
∫
x1 被积函数F包括自变量，未知函数及其导数
x2
泛函的极值 泛函J ( x(t ))在x0 (t ) ∈ S取得极小值是指， 对于任意一个与x0 (t )接近的x(t ) ∈ S，都有J ( x(t ))》J ( x0 (t ))
所谓接近，用距离d ( x(t ), x0 (t )) < ε度量
d[x(t ), x 0 (t )] =
max {| x(t ) · x
t1 ≤ t ≤ t 2
0 ( t ) |, | x' ( t )
· x' 0 (t ) |}
泛函的极大值可类似定义，x0(t)泛函的极值函数或极值曲线
泛函的变分
δx(t ) = x(t ) · x 0 (t )
如同函数的微分是函数增量的线性主部一样，泛函的变分是泛函 增量的线性主部，作为泛函的自变量，函数x(t)在x0(t)的增量记作
(4)
称为函数的变分， 称为函数的变分，由它 引起的泛函的增量记作 · J = J(x 0 (t) + δ x ( t )) · J ( x 0 ( t )) 如果 · J 可以表示为 · J = L ( x 0 (t) , δ x ( t )) + r ( x 0 (t) , δ x ( t )) 的线性项， 其中 L 是 δ x 的线性项，而是 δ J （ x 0 ( t )), δ J （ x ( t )) 的高阶项， δ x 的高阶项， 的变分。 则称 L 为泛函在 x 0 ( t )的变分。记作
泛函的另一个重要形式 是它可以表示为 对参数 α 的导数： · δ J (x(t)) = J ( x (t ) + αδ x (t )) |α = 0 ·α
根据L和r的性质有：
(5)
·J = J ( x(t ) + αδx) · J ( x(t )) = L( x(t ),αδx) + r ( x(t ),αδx)
L( x(t ),αδx) = αL( x(t ),
δx)
α →0
lim
r ( x(t ),αδx)
α
r ( x(t ),αδx) = lim δx = 0 α →0 αδx
J ( x + αδx) · J ( x) · J ( x + αδx) |α =0 = lim ∴ α →0 ·α α J ( x + αδx) + r ( x + αδx) = lim = L ( x , δ x ) = δJ ( x )
α →0
α
极值与变分 利用5式可以得到泛函极值与变分的关系： 5
若J ( x(t ))在x 0 (t )达到极值 则δJ( x 0 (t )) = 0
泛函极值的必要条件——欧拉方程 欧拉方程 泛函极值的必要条件 ）：固定端点条件下取得极值的必要条件 6
d FX · Fx ' = 0 dt Fx · Ftx ' · Fxx ' x'· Fx ' x ' x' ' = 0
推广到含有两个或两个以上未知函数的情况
t2
J ( x ( t ), u ( t )) =
∫ F ( t , x , x ' , u , u ' )dt
t1
的欧拉方程为 d Fx · Fx' = 0 dt d Fu · Fu ' = 0 dt
3）横截条件 如果容许函数x(t)的一个端点t=t2不固定,而是在一条给定的曲线x=g(t) 上变动，讨论泛函J在以上条件下的极值曲线。 1：用欧拉方程得出其通解，用一个端点条件确定一个常数。 2）其次，另一个定解条件用以下式子确定：
[F + (g'· x' )Fx' ] | t = t 2 = 0
称为横截条件 考虑如下两种特殊情况 1）： 当 x = g ( t )垂直于横轴时 , t 2固定但 x ( t 2 )自由 , 称 t 2 为自由端点 ,
dt 2 = 0，所以有 Fx' |t = t 2 = 0
定解条件 2）：
当x = g(t )平行于横轴时 , g' = 0 定解条件为： 定解条件为： F · x' Fx' | t = t 2 = 0
4：条件极值
t
J =
∫
2
F(t,
x(t),
u(t))dt
24 25
t1
x ' ( t ) = f ( t , x ( t ), u ( t ))
引入乘子 λ （ t), 构造泛函
t 21
与函数条件极值一样，采用拉氏乘数法，化为无条件极值。
I(x(t), u(t)) =
∫ [F(t,
x, u) + λ (t)(f(t, x, u) - x' )]dt
26
t1
记 H(t, x, u) = F(t, x, u) + λ (t)f(t, x, u) H 称为哈密尔顿函数，（ 称为哈密尔顿函数，（
t 21
26 ）改写为
I(x(t), u(t)) =
∫ (H
- λ x' )dt
t1
化为含有两个函数x(t),u(t)的无条件极值。用欧拉方程有
d ( H · λx' ) x' = 0 dt d ( H · λx' ) u · ( H · λx' ) u' = 0 dt 将H的表达式代入有 ·H + λ' (t ) = 0 ·x ·H =0 ·u 即 归结为求下列微分方程组 ( H · λx' ) x · ·H = · λ ' (t ) ·x ·H =0 ·u x' = f(t, x, u)
模型五 农作物灭虫药的使用
为了减少虫害给农作物带来的巨大损失，农民们普遍使用农药 冲经济学的角度来看，什麽时候使用灭虫药和使用多少药能让 损失降到最小，是倍受关注的问题，使用一个数学的模型给出 您的解释。 一般地，如果用u(t)表示时刻t的使用灭虫药的数量，用表示x(t) 时刻t害虫的数量，用F[x(t),u(t),t]表示单位时间的总损失，包括被 害虫x(t)毁坏的农作物及灭虫药的费用。设农作物生长季节周期 为T， 则总损失可记作
T
J ( u ( t )) =
F ( x ( t ), u ( t ), t ) dt ∫
(1)
0 又因为害虫数量x(t)极其增长率x’(t)取决于灭虫药的数量u(t)， 所以有
X’(t)=f(x(
t),u(t),t)
(2)
于是（1），（2）构成一个以u(t)为控制函数，x(t)为状态函数 的泛函极值问题。 (参见《实变函数与泛函分析》） 在这里，我们不做一般性的讨论，只就u(t)在特殊情况下的模 型加以考虑,结合实际情况，农名用药的实际情况是：u(t)大体 上成如图的形式: U(t) u2 及隔一段时间用一次药，用药 u1 时间很短（与整个生长季节相比） 于是确定u(t)就转化为确定
τ 1 ,τ ................, u1 , u 2 .............
t 为了进一步简化，在下面的模型中我们假设在整个生长过程中 只使用一次品药。它可以推广到多次的情况。
τ1
τ2
二
模型假设
1。未使用灭虫药时，害虫的自然增长率为r，由于食物丰富 不考虑自身的阻滞作用；害虫的迁移率为常数q>0，表示由外界 向所考察地域迁入；害虫的初始数量为 x0 2.在农作物生长季节内（0 u 0 时才有效， m 是环景保护条 u 例规定的上限。 3.使用单位数量的农药后，害虫减少量与当时数量成正比，比例 系数 α ， 这符合害虫分布较密的情况。 4。农作物被毁坏得数量与当时害虫的数量x(t)成正比，比例系数 为b，农作物的单价为p（时间较短，不考虑折扣因子。） 5:使用灭虫药的固定费用为c 0 ，单位数量灭虫药的费用为c1
τ
三 建立模型 建立模型的目的是确定使用灭虫药的时刻和数量，使整个生 长期间的总损失最小。根据假设4，5总损失应为 T （3）
L(τ , u) = c0 + c1u + pb∫ x(τ , u, t)dt
0
式中
x(τ , u , t ) 表示害虫数量与t,u有关
dx = rx + q, 0 ≤ t < τ dt x ( 0) = x 0
根据假设1，未用灭虫药时（
t <τ
）害虫增长满足
（4）
利用MATHEMATICA 解出它：
In[]=:
DSolve x' t - r x t + q · 0, x t , t
Out[]=:
@D D @D@ @D
0 ≤ t <τ
（5）
q rt x t · +· C 1 r
即：
q rt q x(t ) = ( x0 + )e · r r
根据假设2，3，在 t 满足
= τ 时使用数量的药后害虫的残存量
dx = ·αx, u 0 ≤ u ≤ u m du · x(τ , u 0 ) = x (t )
其中
（6）
x · (τ ) 由（5）式令
t →τ
时得到。
利用MATHEMATICA 解出（6）： In[]=:
DSolve x' u + a x u · 0, x u , u
Out[]:=
x u · ·
即：
-au
C 1
（7）
x(τ,u) = x (t)e
·
·α(u·u0 )
, u0 ≤ u ≤ um
当后害虫又按照方程（4）的规律由初值增长，于是根据（5）式 可以写出
q r ( t ·τ ) q x (t ) = [ x (τ , u ) + ]e · , τ ≤t ≤T r r
（8）
将（6），（7），（8）代入（3）式积分后可得：
·1 e ·1 q e ( x0 + ) + L(τ , u ) = c0 + c1u + pb{ r r r q rτ ·α (u ·u0 ) q qT ·α ( u ·u 0 ) （9） .[( x0 + )e + (1 · e )] · } r r r
rτ
r (T ·τ )
四 模型求解
这实际上是一个求函数极值问题，由高等数学的知识知： 这是一个求二元函数极
值问题，以（u,τ )自变量 在（9）式两边对u求导，并令它等于零有： 可利用MATHEMATIC求偏导
· x f x, y, z
（10）
即： · L = 0
·u
rx 0 1 T τ = · ln( 1 + ) 2 2r q
因为要求 τ 》0，令 τ
（10）
=0
由（10）时可求出
rx 0 q = q c = rT e ·1
所以最佳时刻 τ * 应为
*
（11）
0
（12）
τ =
, q ≤ qc q > qc
rx0 T 1 · ln(1 + ), 2 2r q
（11）式的 令
·L =0 ·u
qc
程临界迁移率 可得
r (T ·τ )
u = u0 +
1
α
ln{
αpb
c1 r
(e
q rτ q · 1)[( x0 + )e · ]} r r
（13）
q < qc
为简化表达式，记
δ (q) =
pbx 0 rT ( e · 1) , r q + rx 0 q 2 pb[ · ] r r
（14） q > qc
则13式可写作
u = u0 +
又因为u 0
1
≤ u ≤ u m ，所以最佳用药量 u *
u0 + um 1
α
ln
αδ
c1
（15） 应为
u =
*
α
ln
αδ
c1
,
,
1<
αδ
c1
< e α ( u m ·u0 )
（16）
αδ
c1
≥e
α ( um ·u0 )
这样，（11），（12），（14），（16）构成了用药佳时刻和 数量的表达式。
五 模型检验
* * 上面所得到的使用灭虫药后的最小损失 L(τ , u ) 应该与不使 用药时的损失小，这时才决定用药。
不使用药的损失是 L(τ ,0) （实际上与 参考三式有
τ
无关）
L(τ ,0) = pb ∫ x(t )dt
0
T
(17)
其中x(t)由（5）式给出，由（17）式计算积分可得
pb q rT L(τ ,0) = [( x0 + )(e · 1) · qT ] r r
将（12），（14），（16）代入（9）式可以算出
（18）
L(τ , u )
* *
经化简后再利用（18）可得：
L (τ , u ) · L (τ ,0 ) =
* *
α
c1
[α u 0 +
αc 0
c1
+ 1 + ln
αδ
c1
·
αδ
c1
]
若记：
（19）
w(q ) = αu 0 +
则可知道仅当条件
αc0
c1
+ 1 + ln
αδ
c1
·
αδ
c1
（20）
W(q)<0 成立时才有：
（21）
L(τ ,0) < c0 + c1u m
（22）
于是在时刻 τ * 使用药量 使用药
是最佳选择。否则，整个生长期应不
模型解释（结果分析） 五 模型解释（结果分析） 在 τ * 的表达式（12）中有一个定值 q ，当实际的害虫迁移率
c
q ≤ qc
时
τ = 0 既生长季节一开始就用药，这是因为q较小
*
害虫的自然增长是虫害主要原因，尽早地用药根除害虫更为有利
q > q c 时外界迁入是虫害的主体，所以要过一段时间用药，并且
q越大灭虫时间越晚，另外，从的 q c 表达式可知，害虫的 初始 值 x 0越大则 q c 越大，增长率r越大则q c 越小。
在
的表达式（16）中规定了
αδ
c1
，因为否则由（20）式 >1
可知 W(q)<0 ，按照（21），（22）式更本不应用药
（16），（14）还表明，衡量药效的系数越大，药的价格越大 则用药量越小；农作物单价越大，衡量农作物损失的系数 越大，害虫的增长率，迁移率，初值越大，则越大。这些都 是与常识相符合。
六 模型评注
模型在适当的假设下得到的结果是合理的，但是由于表达式太 复杂，运用起
来十分不方便。实际上一些农民决定是否用药时 常采用比较简便的准则，比如将不用药的最大损失 与用最大药量的费用 相比较。
L(τ ,0)
当
L(τ ,0) > c0 + c1u m
u m 灭虫，用药时刻另行考虑或按（12）估计
时就用最大药量
当
L(τ ,0) < c0 + c1u m
时就不用药
傅立叶变换在这里的物理意义就是将光的空间分布转换为频率分布（相空间），在靠近原点的部分为图像低频部分，远离原点部分为图像高频部分。
http://blog.csdn.net/yeeman/article/details/6325693
假如空气和水可以给我们的嗅觉味觉以一定程度的刺激，会发生什么
事儿呢？
我们会很悲惨！我们所谓的味觉嗅觉，是我们舌头上和鼻腔粘膜上的感受器
捕捉到了某些特定的分子，触发了神经脉冲；神经脉冲经神经纤维传导至大脑，
触发更多的神经元，产生了感觉——说通俗点，就是放电。如果空气和水能被我
们的嗅味觉器官感知到，那我们的嗅味觉神经通道会永久地处于“放电状态”！
那感觉就像被终身监禁在一个充溢着同一种香水味或臭鸡蛋味的牢房里，永世不
得放风，生不如死
只要打板子的时间间隔很小，每一个板子引起的疼痛都来不及完全衰减，都会对最终的痛苦程度有不同的贡献：
变分法建模
· 1 变分法简介 · 2 应用
问题一： 等周问题（古希腊） 1：给定一平面封闭曲线 Γ ，使得所围的平面图形面积最大。 2：延拓到多维时的情形。
Γ
空间曲面面积的定义：曲面微元向切平面作投影的微元面积， 作和，求极限。 以3维空间为例z=z(x,y),
z |·· =Γ = zΓ
s = min ∫∫ 1 + z + z dxdy
2 x 2 y ·
z |·· =Γ = zΓ
二：Euclid问题 A B
水平镜面 选择P点，使得AP+PB最短
推广的问题，折射。 三： 捷线问题（John.Berluli） A
B 找一条从A到B的连续曲线，当小球只受重力作用， 从A到B的时间最短 1 2 mv = mgy, v = 2 gy 2 等时线，旋轮线 ds
ds = (dx) 2 + (dy ) 2 , dt = v
B xB
( xB , y B )
ds T =∫ = v A
∫
0
1 + y '2 2 gy
dx
四： 最短路问题 A(x1,y1)
y(x) B(x2,y2) 求连接AB的最短线。
L = ∫ 1 + y ' dx
2
1: 平面 2：球面
直线 测地线
变分法简介： 变分法简介：
变分法基本概念 1：变分 设S为一函数集，若对于每一个S中的函数x(t)有一个实数 J与之对应，则称J是定义在S上的泛函 记作J(x(t)),S称为容许函数集
对于平面 xy上过定点 A（x 1 , y 1）和B（x 2 , y 2）的每一条光滑曲线 y ( x )， 绕x轴旋转得到一个旋转体 ，如图，旋转体的侧面 积是曲 如图， 线y ( x )的泛函由微分知识有
x2
s=
∫
2πy ( x ) (1 + y' 2 ( x ))dx
x1
容许函数集为 S = {y(x) | y(x) ∈ C 1 [x 1 , x 2 ], y ( x 1 ) = y 1 , y ( x 2 ) = y 2 } ( 2)
最简泛函的形式：
t2
J ( x(t )) = F(t , x, x' )dt
t1
∫
x1 被积函数F包括自变量，未知函数及其导数
x2
泛函的极值 泛函J ( x(t ))在x0 (t ) ∈ S取得极小值是指， 对于任意一个与x0 (t )接近的x(t ) ∈ S，都有J ( x(t ))》J ( x0 (t ))
所谓接近，用距离d ( x(t ), x0 (t )) < ε度量
d[x(t ), x 0 (t )] =
max {| x(t ) · x
t1 ≤ t ≤ t 2
0 ( t ) |, | x' ( t )
· x' 0 (t ) |}
泛函的极大值可类似定义，x0(t)泛函的极值函数或极值曲线
泛函的变分
δx(t ) = x(t ) · x 0 (t )
如同函数的微分是函数增量的线性主部一样，泛函的变分是泛函 增量的线性主部，作为泛函的自变量，函数x(t)在x0(t)的增量记作
(4)
称为函数的变分， 称为函数的变分，由它 引起的泛函的增量记作 · J = J(x 0 (t) + δ x ( t )) · J ( x 0 ( t )) 如果 · J 可以表示为 · J = L ( x 0 (t) , δ x ( t )) + r ( x 0 (t) , δ x ( t )) 的线性项， 其中 L 是 δ x 的线性项，而是 δ J （ x 0 ( t )), δ J （ x ( t )) 的高阶项， δ x 的高阶项， 的变分。 则称 L 为泛函在 x 0 ( t )的变分。记作
泛函的另一个重要形式 是它可以表示为 对参数 α 的导数： · δ J (x(t)) = J ( x (t ) + αδ x (t )) |α = 0 ·α
根据L和r的性质有：
(5)
·J = J ( x(t ) + αδx) · J ( x(t )) = L( x(t ),αδx) + r ( x(t ),αδx)
L( x(t ),αδx) = αL( x(t ),
δx)
α →0
lim
r ( x(t ),αδx)
α
r ( x(t ),αδx) = lim δx = 0 α →0 αδx
J ( x + αδx) · J ( x) · J ( x + αδx) |α =0 = lim ∴ α →0 ·α α J ( x + αδx) + r ( x + αδx) = lim = L ( x , δ x ) = δJ ( x )
α →0
α
极值与变分 利用5式可以得到泛函极值与变分的关系： 5
若J ( x(t ))在x 0 (t )达到极值 则δJ( x 0 (t )) = 0
泛函极值的必要条件——欧拉方程 欧拉方程 泛函极值的必要条件 ）：固定端点条件下取得极值的必要条件 6
d FX · Fx ' = 0 dt Fx · Ftx ' · Fxx ' x'· Fx ' x ' x' ' = 0
推广到含有两个或两个以上未知函数的情况
t2
J ( x ( t ), u ( t )) =
∫ F ( t , x , x ' , u , u ' )dt
t1
的欧拉方程为 d Fx · Fx' = 0 dt d Fu · Fu ' = 0 dt
3）横截条件 如果容许函数x(t)的一个端点t=t2不固定,而是在一条给定的曲线x=g(t) 上变动，讨论泛函J在以上条件下的极值曲线。 1：用欧拉方程得出其通解，用一个端点条件确定一个常数。 2）其次，另一个定解条件用以下式子确定：
[F + (g'· x' )Fx' ] | t = t 2 = 0
称为横截条件 考虑如下两种特殊情况 1）： 当 x = g ( t )垂直于横轴时 , t 2固定但 x ( t 2 )自由 , 称 t 2 为自由端点 ,
dt 2 = 0，所以有 Fx' |t = t 2 = 0
定解条件 2）：
当x = g(t )平行于横轴时 , g' = 0 定解条件为： 定解条件为： F · x' Fx' | t = t 2 = 0
4：条件极值
t
J =
∫
2
F(t,
x(t),
u(t))dt
24 25
t1
x ' ( t ) = f ( t , x ( t ), u ( t ))
引入乘子 λ （ t), 构造泛函
t 21
与函数条件极值一样，采用拉氏乘数法，化为无条件极值。
I(x(t), u(t)) =
∫ [F(t,
x, u) + λ (t)(f(t, x, u) - x' )]dt
26
t1
记 H(t, x, u) = F(t, x, u) + λ (t)f(t, x, u) H 称为哈密尔顿函数，（ 称为哈密尔顿函数，（
t 21
26 ）改写为
I(x(t), u(t)) =
∫ (H
- λ x' )dt
t1
化为含有两个函数x(t),u(t)的无条件极值。用欧拉方程有
d ( H · λx' ) x' = 0 dt d ( H · λx' ) u · ( H · λx' ) u' = 0 dt 将H的表达式代入有 ·H + λ' (t ) = 0 ·x ·H =0 ·u 即 归结为求下列微分方程组 ( H · λx' ) x · ·H = · λ ' (t ) ·x ·H =0 ·u x' = f(t, x, u)
模型五 农作物灭虫药的使用
为了减少虫害给农作物带来的巨大损失，农民们普遍使用农药 冲经济学的角度来看，什麽时候使用灭虫药和使用多少药能让 损失降到最小，是倍受关注的问题，使用一个数学的模型给出 您的解释。 一般地，如果用u(t)表示时刻t的使用灭虫药的数量，用表示x(t) 时刻t害虫的数量，用F[x(t),u(t),t]表示单位时间的总损失，包括被 害虫x(t)毁坏的农作物及灭虫药的费用。设农作物生长季节周期 为T， 则总损失可记作
T
J ( u ( t )) =
F ( x ( t ), u ( t ), t ) dt ∫
(1)
0 又因为害虫数量x(t)极其增长率x’(t)取决于灭虫药的数量u(t)， 所以有
X’(t)=f(x(
t),u(t),t)
(2)
于是（1），（2）构成一个以u(t)为控制函数，x(t)为状态函数 的泛函极值问题。 (参见《实变函数与泛函分析》） 在这里，我们不做一般性的讨论，只就u(t)在特殊情况下的模 型加以考虑,结合实际情况，农名用药的实际情况是：u(t)大体 上成如图的形式: U(t) u2 及隔一段时间用一次药，用药 u1 时间很短（与整个生长季节相比） 于是确定u(t)就转化为确定
τ 1 ,τ ................, u1 , u 2 .............
t 为了进一步简化，在下面的模型中我们假设在整个生长过程中 只使用一次品药。它可以推广到多次的情况。
τ1
τ2
二
模型假设
1。未使用灭虫药时，害虫的自然增长率为r，由于食物丰富 不考虑自身的阻滞作用；害虫的迁移率为常数q>0，表示由外界 向所考察地域迁入；害虫的初始数量为 x0 2.在农作物生长季节内（0
http://blog.csdn.net/yeeman/article/details/6325693
假如空气和水可以给我们的嗅觉味觉以一定程度的刺激，会发生什么
事儿呢？
我们会很悲惨！我们所谓的味觉嗅觉，是我们舌头上和鼻腔粘膜上的感受器
捕捉到了某些特定的分子，触发了神经脉冲；神经脉冲经神经纤维传导至大脑，
触发更多的神经元，产生了感觉——说通俗点，就是放电。如果空气和水能被我
们的嗅味觉器官感知到，那我们的嗅味觉神经通道会永久地处于“放电状态”！
那感觉就像被终身监禁在一个充溢着同一种香水味或臭鸡蛋味的牢房里，永世不
得放风，生不如死
只要打板子的时间间隔很小，每一个板子引起的疼痛都来不及完全衰减，都会对最终的痛苦程度有不同的贡献：
谈起卷积分当然要先说说冲击函数—-这个倒立的小蝌蚪，卷积其实就是为它诞生的。”冲击函数”是狄拉克为了解决一些瞬间作用的物理现象而提出的符号。
古人曰：”说一堆大道理不如举一个好例子”，冲量这一物理现象很能说明”冲击函数”。在t时间内对一物体作用F的力，我们可以让作用时间t很小，作用力F很大，但让Ft的乘积不变，即冲量不变。于是在用t做横坐标、F做纵坐标的坐标系中，就如同一个面积不变的长方形，底边被挤的窄窄的，高度被挤的高高的，在数学中它可以被挤到无限高，但即使它无限瘦、无限高、但它仍然保持面积不变（它没有被挤没！），为了证实它的存在，可以对它进行积分，积分就是求面积嘛！于是”卷积” 这个数学怪物就这样诞生了。说它是数学怪物是因为追求完美的数学家始终在头脑中转不过来弯，一个能瘦到无限小的家伙，竟能在积分中占有一席之地，必须将这个细高挑清除数学界。但物理学家、工程师们确非常喜欢它，因为它解决了很多当时数学家解决不了的实际问题。最终追求完美的数学家终于想通了，数学是来源于实际的，并最终服务于实际才是真。于是，他们为它量身定做了一套运作规律。于是，妈呀！你我都感觉眩晕的卷积分产生了。
古人曰：”说一堆大道理不如举一个好例子”，冲量这一物理现象很能说明”冲击函数”。在t时间内对一物体作用F的力，我们可以让作用时间t很小，作用力F很大，但让Ft的乘积不变，即冲量不变。于是在用t做横坐标、F做纵坐标的坐标系中，就如同一个面积不变的长方形，底边被挤的窄窄的，高度被挤的高高的，在数学中它可以被挤到无限高，但即使它无限瘦、无限高、但它仍然保持面积不变（它没有被挤没！），为了证实它的存在，可以对它进行积分，积分就是求面积嘛！于是”卷积” 这个数学怪物就这样诞生了。说它是数学怪物是因为追求完美的数学家始终在头脑中转不过来弯，一个能瘦到无限小的家伙，竟能在积分中占有一席之地，必须将这个细高挑清除数学界。但物理学家、工程师们确非常喜欢它，因为它解决了很多当时数学家解决不了的实际问题。最终追求完美的数学家终于想通了，数学是来源于实际的，并最终服务于实际才是真。于是，他们为它量身定做了一套运作规律。于是，妈呀！你我都感觉眩晕的卷积分产生了。
例子：
有一个七品县令，喜欢用打板子来惩戒那些市井无赖，而且有个惯例：如果没犯大罪，只打一板，释放回家，以示爱民如子。
有一个无赖，想出人头地却没啥指望，心想：既然扬不了善名，出恶名也成啊。怎么出恶名？炒作呗！怎么炒作？找名人呀！他自然想到了他的行政长官——县令。
无赖于是光天化日之下，站在县衙门前撒了一泡尿，后果是可想而知地，自然被请进大堂挨了一板子，然后昂首挺胸回家，躺了一天，嘿！身上啥事也没有！第二天如法炮制，全然不顾行政长管的仁慈和衙门的体面，第三天、第四天……每天去县衙门领一个板子回来，还喜气洋洋地，坚持一个月之久！这无赖的名气已经和衙门口的臭气一样，传遍八方了！
县令大人噤着鼻子，呆呆地盯着案子上的惊堂木，拧着眉头思考一个问题：这三十个大板子怎么不好使捏？……想当初，本老爷金榜题名时，数学可是得了满分，今天好歹要解决这个问题：
——人（系统！）挨板子（脉冲！）以后，会有什么表现（输出！）？
——费话，疼呗！
——我问的是：会有什么表现？
——看疼到啥程度。像这无赖的体格，每天挨一个板子啥事都不会有，连哼一下都不可能，你也看到他那得意洋洋的嘴脸了（输出0）；如果一次连揍他十个板子，他可能会皱皱眉头，咬咬牙，硬挺着不哼
（输出1）；揍到二十个板子，他会疼得脸部扭曲，象猪似地哼哼（输出3）；揍到三十个板子，他可能会象驴似地嚎叫，一把鼻涕一把泪地求你饶他一命（输出5）；揍到四十个板子，他会大小便失禁，勉
强哼出声来（输出1）；揍到五十个板子，他连哼一下都不可能（输出0）——死啦！
县令铺开坐标纸，以打板子的个数作为X轴，以哼哼的程度（输出）为Y轴，绘制了一条曲线：
——呜呼呀！这曲线象一座高山，弄不懂弄不懂。为啥那个无赖连挨了三十天大板却不喊绕命呀？
—— 呵呵，你打一次的时间间隔（Δτ=24小时）太长了，所以那个无赖承受的痛苦程度一天一利索，没有叠加，始终是一个常数；如果缩短打板子的时间间隔（建议 Δτ=0.5秒），那他的痛苦程度可就迅速叠加了；等到这无赖挨三十个大板（t=30）时，痛苦程度达到了他能喊叫的极限，会收到最好的惩戒效果，再多打就显示不出您的仁慈了。
——还是不太明白，时间间隔小，为什么痛苦程度会叠加呢？
——这与人（线性时不变系统）对板子（脉冲、输入、激励）的响应有关。什么是响应？人挨一个板子后，疼痛的感觉会在一天（假设的，因人而异）内慢慢消失（衰减），而不可能突然消失。这样一来，只要打板子的时间间隔很小，每一个板子引起的疼痛都来不及完全衰减，都会对最终的痛苦程度有不同的贡献：
t个大板子造成的痛苦程度=Σ(第τ个大板子引起的痛苦*衰减系数)
[衰减系数是（t-τ）的函数，仔细品味]
数学表达为：y(t)=∫T(τ)H(t-τ)
——拿人的痛苦来说卷积的事，太残忍了。除了人以外，其他事物也符合这条规律吗？
——呵呵，县令大人毕竟仁慈。其实除人之外，很多事情也遵循此道。好好想一想，铁丝为什么弯曲一次不折，快速弯曲多次却会轻易折掉呢？
——恩，一时还弄不清，容本官慢慢想来——但有一点是明确地——来人啊，将撒尿的那个无赖抓来，狠打40大板！
有一个七品县令，喜欢用打板子来惩戒那些市井无赖，而且有个惯例：如果没犯大罪，只打一板，释放回家，以示爱民如子。
有一个无赖，想出人头地却没啥指望，心想：既然扬不了善名，出恶名也成啊。怎么出恶名？炒作呗！怎么炒作？找名人呀！他自然想到了他的行政长官——县令。
无赖于是光天化日之下，站在县衙门前撒了一泡尿，后果是可想而知地，自然被请进大堂挨了一板子，然后昂首挺胸回家，躺了一天，嘿！身上啥事也没有！第二天如法炮制，全然不顾行政长管的仁慈和衙门的体面，第三天、第四天……每天去县衙门领一个板子回来，还喜气洋洋地，坚持一个月之久！这无赖的名气已经和衙门口的臭气一样，传遍八方了！
县令大人噤着鼻子，呆呆地盯着案子上的惊堂木，拧着眉头思考一个问题：这三十个大板子怎么不好使捏？……想当初，本老爷金榜题名时，数学可是得了满分，今天好歹要解决这个问题：
——人（系统！）挨板子（脉冲！）以后，会有什么表现（输出！）？
——费话，疼呗！
——我问的是：会有什么表现？
——看疼到啥程度。像这无赖的体格，每天挨一个板子啥事都不会有，连哼一下都不可能，你也看到他那得意洋洋的嘴脸了（输出0）；如果一次连揍他十个板子，他可能会皱皱眉头，咬咬牙，硬挺着不哼
（输出1）；揍到二十个板子，他会疼得脸部扭曲，象猪似地哼哼（输出3）；揍到三十个板子，他可能会象驴似地嚎叫，一把鼻涕一把泪地求你饶他一命（输出5）；揍到四十个板子，他会大小便失禁，勉
强哼出声来（输出1）；揍到五十个板子，他连哼一下都不可能（输出0）——死啦！
县令铺开坐标纸，以打板子的个数作为X轴，以哼哼的程度（输出）为Y轴，绘制了一条曲线：
——呜呼呀！这曲线象一座高山，弄不懂弄不懂。为啥那个无赖连挨了三十天大板却不喊绕命呀？
—— 呵呵，你打一次的时间间隔（Δτ=24小时）太长了，所以那个无赖承受的痛苦程度一天一利索，没有叠加，始终是一个常数；如果缩短打板子的时间间隔（建议 Δτ=0.5秒），那他的痛苦程度可就迅速叠加了；等到这无赖挨三十个大板（t=30）时，痛苦程度达到了他能喊叫的极限，会收到最好的惩戒效果，再多打就显示不出您的仁慈了。
——还是不太明白，时间间隔小，为什么痛苦程度会叠加呢？
——这与人（线性时不变系统）对板子（脉冲、输入、激励）的响应有关。什么是响应？人挨一个板子后，疼痛的感觉会在一天（假设的，因人而异）内慢慢消失（衰减），而不可能突然消失。这样一来，只要打板子的时间间隔很小，每一个板子引起的疼痛都来不及完全衰减，都会对最终的痛苦程度有不同的贡献：
t个大板子造成的痛苦程度=Σ(第τ个大板子引起的痛苦*衰减系数)
[衰减系数是（t-τ）的函数，仔细品味]
数学表达为：y(t)=∫T(τ)H(t-τ)
——拿人的痛苦来说卷积的事，太残忍了。除了人以外，其他事物也符合这条规律吗？
——呵呵，县令大人毕竟仁慈。其实除人之外，很多事情也遵循此道。好好想一想，铁丝为什么弯曲一次不折，快速弯曲多次却会轻易折掉呢？
——恩，一时还弄不清，容本官慢慢想来——但有一点是明确地——来人啊，将撒尿的那个无赖抓来，狠打40大板！
卷积及拉普拉斯变换的通俗解释–对于我这类没学过信号系统的人来说太需要了
卷积(convolution, 另一个通用名称是德文的Faltung)的名称由来，是在于当初定义它时，定义成 integ(f1(v)*f2(t-v))dv，积分区间在0到t之间。举个简单的例子，大家可以看到，为什么叫”卷积”了。比方说在(0，100)间积分，用简单的辛普生积分公式，积分区间分成100等分，那么看到的是f1(0)和f2(100)相乘，f1(1)和f2(99)相乘，f1(2)和f2 (98)相乘，……… 等等等等，就象是在坐标轴上回卷一样。所以人们就叫它”回卷积分”，或者”卷积”了。
为了理解”卷积”的物理意义，不妨将那个问题”相当于它的时域的信号与系统的单位脉冲响应的卷积”略作变化。这个变化纯粹是为了方便表达和理解，不影响任何其它方面。将这个问题表述成这样一个问题：一个信号通过一个系统，系统的响应是频率响应或波谱响应，且看如何理解卷积的物理意义。
假设信号函数为f, 响应函数为g。f不仅是时间的函数(信号时有时无)，还是频率的函数(就算在某一固定时刻，还有的地方大有的地方小)；g也是时间的函数(有时候有反应，有时候没反应)，同时也是频率的函数(不同的波长其响应程度不一样)。那我们要看某一时刻 t 的响应信号，该怎么办呢？
这就需要卷积了。
要看某一时刻 t 的响应信号，自然是看下面两点：
1。你信号来的时候正赶上人家”系统”的响应时间段吗？
2。就算赶上系统响应时间段，响应有多少？
响 应不响应主要是看 f 和 g 两个函数有没有交叠；响应强度的大小不仅取决于所给的信号的强弱，还取决于在某频率处对单位强度响应率。响应强度是信号强弱和对单位强度信号响应率的乘积。”交叠”体现在f(t1)和g(t-t1)上，g之所以是”(t-t1)”就是看两个函数错开多少。
由于 f 和 g 两个函数都有一定的带宽分布(假若不用开头提到的”表述变化”就是都有一定的时间带宽分布)，这个信号响应是在一定”范围”内广泛响应的。算总的响应信号，当然要把所有可能的响应加起来，实际上就是对所有可能t1积分了。积分范围虽然一般在负无穷到正无穷之间；但在没有信号或者没有响应的地方，积也是白积，结果是0，所以往往积分范围可以缩减。
这就是卷积及其物理意义啊。并成一句话来说，就是看一个时有时无(当然作为特例也可以永恒存在)的信号，跟一个响应函数在某一时刻有多大交叠。
, 
，前向差分 forward differencing 
卷积定义上是线性系统分析经常用到的.线性系统就是一个系统的输入和输出的关系是线性关系.就是说整个系统可以分解成N多的无关独立变化,整个系统就是这些变化的累加.
如 x1->y1, x2->y2; 那么A*x1 + B*x2 -> A*y1 + B*y2 这就是线性系统. 表示一个线性系统可以用积分的形式 如 Y = Sf(t,x)g(x)dt S表示积分符号,就是f(t,x)表示的是A B之类的线性系数.
看上去很像卷积呀,,对如果f(t,x) = F(t-x) 不就是了吗.从f(t,x)变成F(t-x)实际上是说明f(t,x)是个线性移不变,就是说 变量的差不变化的时候,那么函数的值不变化. 实际上说明一个事情就是说线性移不变系统的输出可以通过输入和表示系统线性特征的函数卷积得到.
卷积的物理意义？
卷积(convolution, 另一个通用名称是德文的Faltung)的名称由来，是在于当初定义它时，定义成 integ(f1(v)*f2(t-v))dv，积分区间在0到t之间。举个简单的例子，大家可以看到，为什么叫“卷积”了。比方说在(0，100)间积分，用简单的辛普生积分公式，积分区间分成100等分，那么看到的是f1(0)和f2(100)相乘，f1(1)和f2(99)相乘，f1(2)和f2(98)相乘，......... 等等等等，就象是在坐标轴上回卷一样。所以人们就叫它“回卷积分”，或者“卷积”了。
卷积是个啥？我忽然很想从本质上理解它。于是我从抽屉里翻出自己珍藏了许多年，每每下决心阅读却永远都读不完的《应用傅立叶变换》。
3.1 一维卷积的定义
函数f(x)与函数h(x)的卷积，由函参量的无穷积分
定义虽然找到了，但我还是一头雾水。卷积是个无穷积分吗？那它是干啥用的？再往后翻：几何说明、运算举例、基本性质，一堆的公式，就是没有说它是干啥用的。我于是坐在那呆想，忽然第二个困扰我的问题冒了出来：傅立叶变换是个啥？接着就是第三个、第四个、……、第N个问题。
傅立叶变换是个啥？听说能将时域上的东东变到频域上分析？哎？是变到频域上还是空间域上来着？到底啥是时域，频域，空间域？
上网查傅立叶变换的物理意义，没发现明确答案，倒发现了许多和我一样晕着问问题的人。结果又多出了许多名词，能量？功率谱？图像灰度域？……没办法又去翻那本教材。
1.1 一维傅立叶变换的定义与傅立叶积分定理
设f(x)是实变量x的函数，该函数可实可复，称积分
为函数f(x)的傅立叶变换。
吐血，啥是无穷积分来着？积分是啥来着？还能记起三角函数和差化积、积化和差公式吗？我忽然有种想把高中课本寻来重温的冲动。
卷积公式 解释 卷积公式是用来求随机变量和的密度函数(pdf)的计算公式。 定义式： z(t)=x(t)*y(t)= ∫x(m)y(t-m)dm. 已知x,y的pdf,x(t),y(t).现在要求z=x+y的pdf. 我们作变量替显，令 z=x+y,m=x. 雅可比行列式=1.那么,z，m联合密度就是f(z,m)=x(m)y(z-m)*1. 这样，就可以很容易求Z的在（z,m)中边缘分布 即fZ(z)=∫x(m)y(z-m)dm..... 由于这个公式和x(t),y(t)存在一一对应的关系。为了方便，所以记 ∫x(m)y(z-m)dm=x(t)*y(t) 长度为m的向量序列u和长度为n的向量序列v，卷积w的向量序列长度为(m+n-1), u(n)与v(n)的卷积w(n)定义为： w(n)=u(n)@v(n)=sum(v(m)*u(n-m)),m from 负无穷到正无穷； 当m=n时w(1) = u(1)*v(1) w(2) = u(1)*v(2)+u(2)*v(1) w(3) = u(1)*v(3)+u(2)*v(2)+u(3)*v(1) … w(n) = u(1)*v(n)+u(2)*v(n-1)+ … +u(n)*v(1) … w(2*n-1) = u(n)*v(n) 当m≠n时,应以0补齐阶次低的向量的高位后进行计算 这是数学中常用的一个公式，在概率论中，是个重点也是一个难点。
卷积公式是用来求随机变量和的密度函数(pdf)的计算公式。
定义式：
z(t)=x(t)*y(t)= ∫x(m)y(t-m)dm.
已知x,y的pdf,x(t),y(t).现在要求z=x+y的pdf. 我们作变量替显，令
z=x+y,m=x. 雅可比行列式=1.那么,t，m联合密度就是f(z,m)=x(m)y(z-m)*1. 这样，就可以很容易求Z的在（z,m)中边缘分布
即fZ(z)=∫x(m)y(z-m)dm..... 由于这个公式和x(t),y(t)存在一一对应的关系。为了方便，所以记 ∫x(m)y(z-m)dm=x(t)*y(t)
自己平时看了一些论文，但老感觉看完过后就会慢慢的淡忘，某一天重新拾起来的时候又好像没有看过一样。所以想习惯地把一些感觉有用的论文中的知识点总结整理一下，一方面在整理过程中，自己的理解也会更深，另一方面也方便未来自己的勘察。更好的还可以放到博客上面与大家交流。因为基础有限，所以对论文的一些理解可能不太正确，还望大家不吝指正交流，谢谢。
本文的论文来自：
Notes on Convolutional Neural Networks, Jake Bouvrie。
这个主要是CNN的推导和实现的一些笔记，再看懂这个笔记之前，最好具有CNN的一些基础。这里也先列出一个资料供参考：
[1] Deep Learning（深度学习）学习笔记整理系列之（七）
[2] LeNet-5, convolutional neural networks
[3]卷积神经网络
[4] Neural Network for Recognition of Handwritten Digits
[5] Deep learning：三十八(Stacked CNN简单介绍)
[6] Gradient-based learning applied to document recognition.
[7]Imagenet classification with deep convolutional neural networks.
[8] UFLDL中的“卷积特征提取”和“池化”。
另外，这里有个matlab的Deep Learning的toolbox，里面包含了CNN的代码，在下一个博文中，我将会详细注释这个代码。这个笔记对这个代码的理解非常重要。
下面是自己对其中的一些知识点的理解：
这个文档讨论的是CNNs的推导和实现。CNN架构的连接比权值要多很多，这实际上就隐含着实现了某种形式的规则化。这种特别的网络假定了我们希望通过数据驱动的方式学习到一些滤波器，作为提取输入的特征的一种方法。
本文中，我们先对训练全连接网络的经典BP算法做一个描述，然后推导2D CNN网络的卷积层和子采样层的BP权值更新方法。在推导过程中，我们更强调实现的效率，所以会给出一些Matlab代码。最后，我们转向讨论如何自动地学习组合前一层的特征maps，特别地，我们还学习特征maps的稀疏组合。
二、全连接的反向传播算法
典型的CNN中，开始几层都是卷积和下采样的交替，然后在最后一些层（靠近输出层的），都是全连接的一维网络。这时候我们已经将所有两维2D的特征maps转化为全连接的一维网络的输入。这样，当你准备好将最终的2D特征maps输入到1D网络中时，一个非常方便的方法就是把所有输出的特征maps连接成一个长的输入向量。然后我们回到BP算法的讨论。（更详细的基础推导可以参考UFLDL中“反向传导算法”）。
2.1、Feedforward Pass前向传播
在下面的推导中，我们采用平方误差代价函数。我们讨论的是多类问题，共c类，共N个训练样本。
这里
表示第n个样本对应的标签的第k维。
表示第n个样本对应的网络输出的第k个输出。对于多类问题，输出一般组织为“one-of-c”的形式，也就是只有该输入对应的类的输出节点输出为正，其他类的位或者节点为0或者负数，这个取决于你输出层的激活函数。sigmoid就是0，tanh就是-1.
因为在全部训练集上的误差只是每个训练样本的误差的总和，所以这里我们先考虑对于一个样本的BP。对于第n个样本的误差，表示为：
传统的全连接神经网络中，我们需要根据BP规则计算代价函数E关于网络每一个权值的偏导数。我们用l来表示当前层，那么当前层的输出可以表示为：
输出激活函数f(.)可以有很多种，一般是sigmoid函数或者双曲线正切函数。sigmoid将输出压缩到[0, 1]，所以最后的输出平均值一般趋于0 。所以如果将我们的训练数据归一化为零均值和方差为1，可以在梯度下降的过程中增加收敛性。对于归一化的数据集来说，双曲线正切函数也是不错的选择。
2.2、Backpropagation Pass反向传播
反向传播回来的误差可以看做是每个神经元的基的灵敏度sensitivities（灵敏度的意思就是我们的基b变化多少，误差会变化多少，也就是误差对基的变化率，也就是导数了），定义如下：（第二个等号是根据求导的链式法则得到的）
因为∂u/∂b=1，所以∂E/∂b=∂E/∂u=δ，也就是说bias基的灵敏度∂E/∂b=δ和误差E对一个节点全部输入u的导数∂E/∂u是相等的。这个导数就是让高层误差反向传播到底层的神来之笔。反向传播就是用下面这条关系式：（下面这条式子表达的就是第l层的灵敏度，就是）
公式（1）
这里的“◦”表示每个元素相乘。输出层的神经元的灵敏度是不一样的：
最后，对每个神经元运用delta（即δ）规则进行权值更新。具体来说就是，对一个给定的神经元，得到它的输入，然后用这个神经元的delta（即δ）来进行缩放。用向量的形式表述就是，对于第l层，误差对于该层每一个权值（组合为矩阵）的导数是该层的输入（等于上一层的输出）与该层的灵敏度（该层每个神经元的δ组合成一个向量的形式）的叉乘。然后得到的偏导数乘以一个负学习率就是该层的神经元的权值的更新了：
公式（2）
对于bias基的更新表达式差不多。实际上，对于每一个权值(W)ij都有一个特定的学习率ηIj。
三、Convolutional Neural Networks 卷积神经网络
3.1、Convolution Layers 卷积层
我们现在关注网络中卷积层的BP更新。在一个卷积层，上一层的特征maps被一个可学习的卷积核进行卷积，然后通过一个激活函数，就可以得到输出特征map。每一个输出map可能是组合卷积多个输入maps的值：
这里Mj表示选择的输入maps的集合，那么到底选择哪些输入maps呢？有选择一对的或者三个的。但下面我们会讨论如何去自动选择需要组合的特征maps。每一个输出map会给一个额外的偏置b，但是对于一个特定的输出map，卷积每个输入maps的卷积核是不一样的。也就是说，如果输出特征map j和输出特征map k都是从输入map i中卷积求和得到，那么对应的卷积核是不一样的。
3.1.1、Computing the Gradients梯度计算
我们假定每个卷积层l都会接一个下采样层l+1 。对于BP来说，根据上文我们知道，要想求得层l的每个神经元对应的权值的权值更新，就需要先求层l的每一个神经节点的灵敏度δ（也就是权值更新的公式（2））。为了求这个灵敏度我们就需要先对下一层的节点（连接到当前层l的感兴趣节点的第l+1层的节点）的灵敏度求和（得到δl+1），然后乘以这些连接对应的权值（连接第l层感兴趣节点和第l+1层节点的权值）W。再乘以当前层l的该神经元节点的输入u的激活函数f的导数值（也就是那个灵敏度反向传播的公式（1）的δl的求解），这样就可以得到当前层l每个神经节点对应的灵敏度δl了。
然而，因为下采样的存在，采样层的一个像素（神经元节点）对应的灵敏度δ对应于卷积层（上一层）的输出map的一块像素（采样窗口大小）。因此，层l中的一个map的每个节点只与l+1层中相应map的一个节点连接。
为了有效计算层l的灵敏度，我们需要上采样upsample 这个下采样downsample层对应的灵敏度map（特征map中每个像素对应一个灵敏度，所以也组成一个map），这样才使得这个灵敏度map大小与卷积层的map大小一致，然后再将层l的map的激活值的偏导数与从第l+1层的上采样得到的灵敏度map逐元素相乘（也就是公式（1））。
在下采样层map的权值都取一个相同值β，而且是一个常数。所以我们只需要将上一个步骤得到的结果乘以一个β就可以完成第l层灵敏度δ的计算。
我们可以对卷积层中每一个特征map j重复相同的计算过程。但很明显需要匹配相应的子采样层的map（参考公式（1））：
up(.)表示一个上采样操作。如果下采样的采样因子是n的话，它简单的将每个像素水平和垂直方向上拷贝n次。这样就可以恢复原来的大小了。实际上，这个函数可以用Kronecker乘积来实现：
好，到这里，对于一个给定的map，我们就可以计算得到其灵敏度map了。然后我们就可以通过简单的对层l中的灵敏度map中所有节点进行求和快速的计算bias基的梯度了：
公式（3）
最后，对卷积核的权值的梯度就可以用BP算法来计算了（公式（2））。另外，很多连接的权值是共享的，因此，对于一个给定的权值，我们需要对所有与该权值有联系（权值共享的连接）的连接对该点求梯度，然后对这些梯度进行求和，就像上面对bias基的梯度计算一样：
这里，
是
中的在卷积的时候与
逐元素相乘的patch，输出卷积map的(u, v)位置的值是由上一层的(u, v)位置的patch与卷积核k_ij逐元素相乘的结果。
咋一看，好像我们需要煞费苦心地记住输出map（和对应的灵敏度map）每个像素对应于输入map的哪个patch。但实际上，在Matlab中，可以通过一个代码就实现。对于上面的公式，可以用Matlab的卷积函数来实现：
我们先对delta灵敏度map进行旋转，这样就可以进行互相关计算，而不是卷积（在卷积的数学定义中，特征矩阵（卷积核）在传递给conv2时需要先翻转（flipped）一下。也就是颠倒下特征矩阵的行和列）。然后把输出反旋转回来，这样我们在前向传播进行卷积的时候，卷积核才是我们想要的方向。
3.2、Sub-sampling Layers 子采样层
对于子采样层来说，有N个输入maps，就有N个输出maps，只是每个输出map都变小了。
down(.)表示一个下采样函数。典型的操作一般是对输入图像的不同nxn的块的所有像素进行求和。这样输出图像在两个维度上都缩小了n倍。每个输出map都对应一个属于自己的乘性偏置β和一个加性偏置b。
3.2.1、Computing the Gradients 梯度计算
这里最困难的是计算灵敏度map。一旦我们得到这个了，那我们唯一需要更新的偏置参数β和b就可以轻而易举了（公式（3））。如果下一个卷积层与这个子采样层是全连接的，那么就可以通过BP来计算子采样层的灵敏度maps。
我们需要计算卷积核的梯度，所以我们必须找到输入map中哪个patch对应输出map的哪个像素。这里，就是必须找到当前层的灵敏度map中哪个patch对应与下一层的灵敏度map的给定像素，这样才可以利用公式（1）那样的δ递推，也就是灵敏度反向传播回来。另外，需要乘以输入patch与输出像素之间连接的权值，这个权值实际上就是卷积核的权值（已旋转的）。
在这之前，我们需要先将核旋转一下，让卷积函数可以实施互相关计算。另外，我们需要对卷积边界进行处理，但在Matlab里面，就比较容易处理。Matlab中全卷积会对缺少的输入像素补0 。
到这里，我们就可以对b和β计算梯度了。首先，加性基b的计算和上面卷积层的一样，对灵敏度map中所有元素加起来就可以了：
而对于乘性偏置β，因为涉及到了在前向传播过程中下采样map的计算，所以我们最好在前向的过程中保存好这些maps，这样在反向的计算中就不用重新计算了。我们定义：
这样，对β的梯度就可以用下面的方式计算：
3.3、Learning Combinations of Feature Maps 学习特征map的组合
大部分时候，通过卷积多个输入maps，然后再对这些卷积值求和得到一个输出map，这样的效果往往是比较好的。在一些文献中，一般是人工选择哪些输入maps去组合得到一个输出map。但我们这里尝试去让CNN在训练的过程中学习这些组合，也就是让网络自己学习挑选哪些输入maps来计算得到输出map才是最好的。我们用αij表示在得到第j个输出map的其中第i个输入map的权值或者贡献。这样，第j个输出map可以表示为：
需要满足约束：
这些对变量αij的约束可以通过将变量αij表示为一个组无约束的隐含权值cij的softmax函数来加强。（因为softmax的因变量是自变量的指数函数，他们的变化率会不同）。
因为对于一个固定的j来说，每组权值cij都是和其他组的权值独立的，所以为了方面描述，我们把下标j去掉，只考虑一个map的更新，其他map的更新是一样的过程，只是map的索引j不同而已。
Softmax函数的导数表示为：
这里的δ是Kronecker delta。对于误差对于第l层变量αi的导数为：
最后就可以通过链式规则去求得代价函数关于权值ci的偏导数了：
3.3.1、Enforcing Sparse Combinations 加强稀疏性组合
为了限制αi是稀疏的，也就是限制一个输出map只与某些而不是全部的输入maps相连。我们在整体代价函数里增加稀疏约束项Ω(α)。对于单个样本，重写代价函数为：
然后寻找这个规则化约束项对权值ci求导的贡献。规则化项Ω(α)对αi求导是：
然后，通过链式法则，对ci的求导是：
所以，权值ci最后的梯度是：
3.4、Making it Fast with MATLAB
CNN的训练主要是在卷积层和子采样层的交互上，其主要的计算瓶颈是：
1）前向传播过程：下采样每个卷积层的maps；
2）反向传播过程：上采样高层子采样层的灵敏度map，以匹配底层的卷积层输出maps的大小；
3）sigmoid的运用和求导。
对于第一和第二个问题，我们考虑的是如何用Matlab内置的图像处理函数去实现上采样和下采样的操作。对于上采样，imresize函数可以搞定，但需要很大的开销。一个比较快速的版本是使用Kronecker乘积函数kron。通过一个全一矩阵ones来和我们需要上采样的矩阵进行Kronecker乘积，就可以实现上采样的效果。对于前向传播过程中的下采样，imresize并没有提供在缩小图像的过程中还计算nxn块内像素的和的功能，所以没法用。一个比较好和快速的方法是用一个全一的卷积核来卷积图像，然后简单的通过标准的索引方法来采样最后卷积结果。例如，如果下采样的域是2x2的，那么我们可以用2x2的元素全是1的卷积核来卷积图像。然后再卷积后的图像中，我们每个2个点采集一次数据，y=x(1:2:end,1:2:end)，这样就可以得到了两倍下采样，同时执行求和的效果。
对于第三个问题，实际上有些人以为Matlab中对sigmoid函数进行inline的定义会更快，其实不然，Matlab与C/C++等等语言不一样，Matlab的inline反而比普通的函数定义更非时间。所以，我们可以直接在代码中使用计算sigmoid函数及其导数的真实代码。
卷积(convolution, 另一个通用名称是德文的Faltung)的名称由来，是在于当初定义它时，定义成 integ(f1(v)*f2(t-v))dv，积分区间在0到t之间。举个简单的例子，大家可以看到，为什么叫”卷积”了。比方说在(0，100)间积分，用简单的辛普生积分公式，积分区间分成100等分，那么看到的是f1(0)和f2(100)相乘，f1(1)和f2(99)相乘，f1(2)和f2 (98)相乘，……… 等等等等，就象是在坐标轴上回卷一样。所以人们就叫它”回卷积分”，或者”卷积”了。
为了理解”卷积”的物理意义，不妨将那个问题”相当于它的时域的信号与系统的单位脉冲响应的卷积”略作变化。这个变化纯粹是为了方便表达和理解，不影响任何其它方面。将这个问题表述成这样一个问题：一个信号通过一个系统，系统的响应是频率响应或波谱响应，且看如何理解卷积的物理意义。
假设信号函数为f, 响应函数为g。f不仅是时间的函数(信号时有时无)，还是频率的函数(就算在某一固定时刻，还有的地方大有的地方小)；g也是时间的函数(有时候有反应，有时候没反应)，同时也是频率的函数(不同的波长其响应程度不一样)。那我们要看某一时刻 t 的响应信号，该怎么办呢？
这就需要卷积了。
要看某一时刻 t 的响应信号，自然是看下面两点：
1。你信号来的时候正赶上人家”系统”的响应时间段吗？
2。就算赶上系统响应时间段，响应有多少？
响 应不响应主要是看 f 和 g 两个函数有没有交叠；响应强度的大小不仅取决于所给的信号的强弱，还取决于在某频率处对单位强度响应率。响应强度是信号强弱和对单位强度信号响应率的乘积。”交叠”体现在f(t1)和g(t-t1)上，g之所以是”(t-t1)”就是看两个函数错开多少。
由于 f 和 g 两个函数都有一定的带宽分布(假若不用开头提到的”表述变化”就是都有一定的时间带宽分布)，这个信号响应是在一定”范围”内广泛响应的。算总的响应信号，当然要把所有可能的响应加起来，实际上就是对所有可能t1积分了。积分范围虽然一般在负无穷到正无穷之间；但在没有信号或者没有响应的地方，积也是白积，结果是0，所以往往积分范围可以缩减。
这就是卷积及其物理意义啊。并成一句话来说，就是看一个时有时无(当然作为特例也可以永恒存在)的信号，跟一个响应函数在某一时刻有多大交叠。
图像处理－线性滤波－1 基础（相关算子、卷积算子、边缘效应）
这里讨论利用输入图像中像素的小邻域来产生输出图像的方法，在信号处理中这种方法称为滤波（filtering）。其中，最常用的是线性滤波：输出像素是输入邻域像素的加权和。
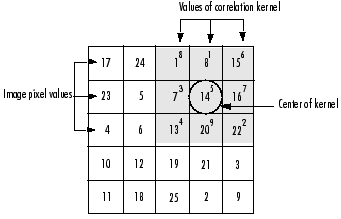
1.相关算子（Correlation Operator)
, 
步骤：
例：
A = [1724 1 8 15 h = [8 1 6
23 5 7 14 16 3 5 7
4 6 13 20 22 4 9 2]
10 12 19 21 3
11 18 25 2 9] 计算输出图像的（2，4）元素=Matlab 函数：imfilter(A,h)
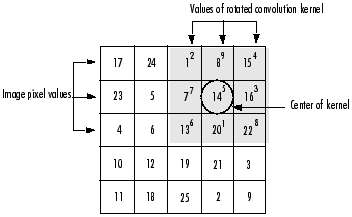
2.卷积算子（Convolution)
定义：
， 
，其中
步骤：
Matlab 函数：Matlab 函数：imfilter(A,h,'conv')% imfilter默认是相关算子，因此当进行卷积计算时需要传入参数'conv'
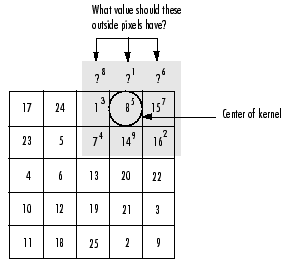
3.边缘效应
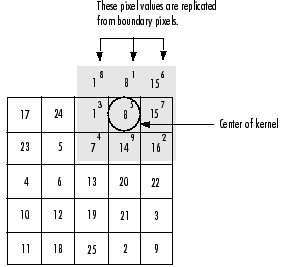
当对图像边缘的进行滤波时，核的一部分会位于图像边缘外面。
常用的策略包括：
1）使用常数填充：imfilter默认用0填充，这会造成处理后的图像边缘是黑色的。2）复制边缘像素：I3 = imfilter(I,h,'replicate');
4.常用滤波
fspecial函数可以生成几种定义好的滤波器的相关算子的核。
例：unsharp masking 滤波
I = imread('moon.tif');h = fspecial('unsharp');I2 = imfilter(I,h);imshow(I), title('Original Image')figure, imshow(I2), title('Filtered Image')
图像处理－线性滤波－2 图像微分（1、2阶导数和拉普拉斯算子）
更复杂些的滤波算子一般是先利用高斯滤波来平滑，然后计算其1阶和2阶微分。由于它们滤除高频和低频，因此称为带通滤波器（band-pass filters）。
在介绍具体的带通滤波器前，先介绍必备的图像微分知识。
1 一阶导数
连续函数，其微分可表达为
对于离散情况（图像），其导数必须用差分方差来近似，有
，前向差分 forward differencing 
1）前向差分的Matlab实现
function dimg = mipforwarddiff(img,direction)% MIPFORWARDDIFFFinite difference calculations %%DIMG = MIPFORWARDDIFF(IMG,DIRECTION) %%Calculates the forward-difference fora given direction%IMG : input image %DIRECTION : 'dx'or'dy'%DIMG : resultant image %%See also MIPCENTRALDIFF MIPBACKWARDDIFF MIPSECONDDERIV %MIPSECONDPARTIALDERIV %Omer Demirkaya, Musa Asyali, Prasana Shaoo, ... 9/1/06 %Medical Image Processing Toolbox imgPad = padarray(img,[1 1],'symmetric','both');%将原图像的边界扩展[row,col] = size(imgPad);dimg = zeros(row,col);switch(direction)case'dx',dimg(:,1:col-1) = imgPad(:,2:col)-imgPad(:,1:col-1);%x方向差分计算，case'dy',dimg(1:row-1,:) = imgPad(2:row,:)-imgPad(1:row-1,:);otherwise, disp('Direction is unknown');end;dimg = dimg(2:end-1,2:end-1);
2）中心差分的Matlab实现
function dimg = mipcentraldiff(img,direction)% MIPCENTRALDIFFFinite difference calculations %%DIMG = MIPCENTRALDIFF(IMG,DIRECTION) %%Calculates the central-difference fora given direction%IMG : input image %DIRECTION : 'dx'or'dy'%DIMG : resultant image %%See also MIPFORWARDDIFF MIPBACKWARDDIFF MIPSECONDDERIV %MIPSECONDPARTIALDERIV %Omer Demirkaya, Musa Asyali, Prasana Shaoo, ... 9/1/06 %Medical Image Processing Toolbox img = padarray(img,[1 1],'symmetric','both');[row,col] = size(img);dimg = zeros(row,col);switch(direction)case'dx',dimg(:,2:col-1) = (img(:,3:col)-img(:,1:col-2))/2;case'dy',dimg(2:row-1,:) = (img(3:row,:)-img(1:row-2,:))/2;otherwise,disp('Direction is unknown');enddimg = dimg(2:end-1,2:end-1);
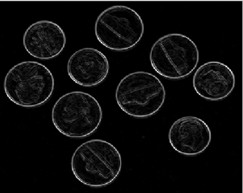
实例：技术图像x方向导数
I = imread('coins.png'); figure; imshow(I);Id = mipforwarddiff(I,'dx'); figure, imshow(Id);
原图像 x方向1阶导数
2 图像梯度（Image Gradient）
图像I的梯度定义为
Matlab函数
1）gradient：梯度计算2）quiver：以箭头形状绘制梯度。注意放大下面最右侧图可看到箭头，由于这里计算横竖两个方向的梯度，因此箭头方向都是水平或垂直的。
实例：仍采用上面的原始图像
I =double(imread('coins.png'));[dx,dy]=gradient(I);magnitudeI=sqrt(dx.^2+dy.^2);figure;imagesc(magnitudeI);colormap(gray);%梯度幅值hold on;quiver(dx,dy);%叠加梯度方向
3 二阶导数
对于一维函数，其二阶导数
3.1 普拉斯算子（laplacian operator）
3.1.2 概念
拉普拉斯算子是n维欧式空间的一个二阶微分算子。它定义为两个梯度向量算子的内积
其在二维空间上的公式为：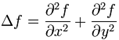 
对于1维离散情况，其二阶导数变为二阶差分
1）首先，其一阶差分为
2）因此，二阶差分为
实现
对于2维离散情况（图像），拉普拉斯算子是2个维上二阶差分的和（见式3.3），其公式为：
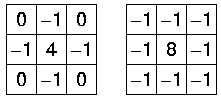
上式对应的卷积核为
常用的拉普拉斯核有：
3.1.2 应用
拉普拉斯算子会突出像素值快速变化的区域，因此常用于边缘检测。
Matlab里有两个函数
1）del2
计算公式：
， 
2）fspecial：图像处理中一般利用Matlab函数fspecial
h = fspecial('laplacian', alpha) returns a 3-by-3 filter approximating the shape of the two-dimensional Laplacian operator.
The parameter alpha controls the shape of the Laplacian and must be in the range 0.0 to 1.0. The default value for alpha is 0.2.
The parameter alpha controls the shape of the Laplacian and must be in the range 0.0 to 1.0. The default value for alpha is 0.2.
3.1.3 资源
http://fourier.eng.hmc.edu/e161/lectures/gradient/node8.html
sift算法
尺度不变特征转换(Scale-invariant feature transform
Sift算法就是用不同尺度（标准差）的高斯函数对图像进行平滑，然后比较平滑后图像的差别，
差别大的像素就是特征明显的点。
差别大的像素就是特征明显的点。
sift可以同时处理亮度，平移，旋转，尺度的变化，利用特征点来提取特征描述符，最后在特征描述符之间寻找匹配
五个步骤
1构建尺度空间，检测极值点，获得尺度不变性
2特征点过滤并进行经确定位，剔除不稳定的特征点
3 在特征点处提取特征描述符，为特征点分配方向直
4声称特征描述子，利用特征描述符寻找匹配点
5计算变换参数
当2幅图像的sift特征向量生成以后，下一步就可以采用关键点特征向量的欧式距离来作为2幅图像中关键点的相似性判定量度
尺度空间：
尺度就是受delta这个参数控制的表示
而不同的L(x,y,delta)就构成了尺度空间，实际上具体计算的时候即使连续的高斯函数，都要被离散为矩阵来和数字图像进行卷积操作
L(x,y,delta)=G(x,y,e)*i(x,y)
尺度空间＝原始图像（卷积）一个可变尺度的2维高斯函数G(x,y,e)
G(x,y,e) = [1/2*pi*e^2] * exp[ -(x^2 + y^2)/2e^2]
为了更有效的在尺度空间检测到稳定的关键点，提出了高斯差分尺度空间，利用不同尺度的高斯差分核与原始图像i(x,y)卷积生成
D(x,y,e)=(G(x,y,ke)-G(x,y,e))*i(x,y)
=L(x,y,ke)-L(x,y,e)
(为避免遍历每个像素点)
高斯卷积：
在组建一组尺度空间后，再组建下一组尺度空间，对上一组尺度空间的最后一幅图像进行二分之一采样，得到下一组尺度空间的第一幅图像，然后进行像建立第一组尺度空间那样的操作，得到第二组尺度空间，公式定义为
高斯差分
图像处理之卷积概念
我们来看一下一维卷积的概念.
连续空间的卷积定义是 f(x)与g(x)的卷积是 f(t-x)g(x) 在t从负无穷到正无穷的积分值.t-x要在f(x)定义域内,所以看上去很大的积分实际上还是在一定范围的.
实际的过程就是f(x) 先做一个Y轴的反转,然后再沿X轴平移t就是f(t-x),然后再把g(x)拿来,两者乘积的值再积分.想象一下如果g(x)或者f(x)是个单位的阶越函数. 那么就是f(t-x)与g(x)相交部分的面积.这就是卷积了.
把积分符号换成求和就是离散空间的卷积定义了.
连续空间的卷积定义是 f(x)与g(x)的卷积是 f(t-x)g(x) 在t从负无穷到正无穷的积分值.t-x要在f(x)定义域内,所以看上去很大的积分实际上还是在一定范围的.
实际的过程就是f(x) 先做一个Y轴的反转,然后再沿X轴平移t就是f(t-x),然后再把g(x)拿来,两者乘积的值再积分.想象一下如果g(x)或者f(x)是个单位的阶越函数. 那么就是f(t-x)与g(x)相交部分的面积.这就是卷积了.
把积分符号换成求和就是离散空间的卷积定义了.
那么在图像中卷积卷积地是什么意思呢,就是图像f(x),模板g(x),然后将模版g(x)在模版中移动,每到一个位置,就把f(x)与g(x)的定义域相交的元素进行乘积并且求和,得出新的图像一点,就是被卷积后的图像. 模版又称为卷积核.卷积核做一个矩阵的形状.
卷积定义上是线性系统分析经常用到的.线性系统就是一个系统的输入和输出的关系是线性关系.就是说整个系统可以分解成N多的无关独立变化,整个系统就是这些变化的累加.
如 x1->y1, x2->y2; 那么A*x1 + B*x2 -> A*y1 + B*y2 这就是线性系统. 表示一个线性系统可以用积分的形式 如 Y = Sf(t,x)g(x)dt S表示积分符号,就是f(t,x)表示的是A B之类的线性系数.
看上去很像卷积呀,,对如果f(t,x) = F(t-x) 不就是了吗.从f(t,x)变成F(t-x)实际上是说明f(t,x)是个线性移不变,就是说 变量的差不变化的时候,那么函数的值不变化. 实际上说明一个事情就是说线性移不变系统的输出可以通过输入和表示系统线性特征的函数卷积得到.
谈起卷积分当然要先说说冲击函数—-这个倒立的小蝌蚪，卷积其实就是为它诞生的。”冲击函数”是狄拉克为了解决一些瞬间作用的物理现象而提出的符号。
古人曰：”说一堆大道理不如举一个好例子”，冲量这一物理现象很能说明”冲击函数”。在t时间内对一物体作用F的力，我们可以让作用时间t很小，作用力F很大，但让Ft的乘积不变，即冲量不变。于是在用t做横坐标、F做纵坐标的坐标系中，就如同一个面积不变的长方形，底边被挤的窄窄的，高度被挤的高高的，在数学中它可以被挤到无限高，但即使它无限瘦、无限高、但它仍然保持面积不变（它没有被挤没！），为了证实它的存在，可以对它进行积分，积分就是求面积嘛！于是”卷积” 这个数学怪物就这样诞生了。说它是数学怪物是因为追求完美的数学家始终在头脑中转不过来弯，一个能瘦到无限小的家伙，竟能在积分中占有一席之地，必须将这个细高挑清除数学界。但物理学家、工程师们确非常喜欢它，因为它解决了很多当时数学家解决不了的实际问题。最终追求完美的数学家终于想通了，数学是来源于实际的，并最终服务于实际才是真。于是，他们为它量身定做了一套运作规律。于是，妈呀！你我都感觉眩晕的卷积分产生了。
古人曰：”说一堆大道理不如举一个好例子”，冲量这一物理现象很能说明”冲击函数”。在t时间内对一物体作用F的力，我们可以让作用时间t很小，作用力F很大，但让Ft的乘积不变，即冲量不变。于是在用t做横坐标、F做纵坐标的坐标系中，就如同一个面积不变的长方形，底边被挤的窄窄的，高度被挤的高高的，在数学中它可以被挤到无限高，但即使它无限瘦、无限高、但它仍然保持面积不变（它没有被挤没！），为了证实它的存在，可以对它进行积分，积分就是求面积嘛！于是”卷积” 这个数学怪物就这样诞生了。说它是数学怪物是因为追求完美的数学家始终在头脑中转不过来弯，一个能瘦到无限小的家伙，竟能在积分中占有一席之地，必须将这个细高挑清除数学界。但物理学家、工程师们确非常喜欢它，因为它解决了很多当时数学家解决不了的实际问题。最终追求完美的数学家终于想通了，数学是来源于实际的，并最终服务于实际才是真。于是，他们为它量身定做了一套运作规律。于是，妈呀！你我都感觉眩晕的卷积分产生了。
例子：
有一个七品县令，喜欢用打板子来惩戒那些市井无赖，而且有个惯例：如果没犯大罪，只打一板，释放回家，以示爱民如子。
有一个无赖，想出人头地却没啥指望，心想：既然扬不了善名，出恶名也成啊。怎么出恶名？炒作呗！怎么炒作？找名人呀！他自然想到了他的行政长官——县令。
无赖于是光天化日之下，站在县衙门前撒了一泡尿，后果是可想而知地，自然被请进大堂挨了一板子，然后昂首挺胸回家，躺了一天，嘿！身上啥事也没有！第二天如法炮制，全然不顾行政长管的仁慈和衙门的体面，第三天、第四天……每天去县衙门领一个板子回来，还喜气洋洋地，坚持一个月之久！这无赖的名气已经和衙门口的臭气一样，传遍八方了！
县令大人噤着鼻子，呆呆地盯着案子上的惊堂木，拧着眉头思考一个问题：这三十个大板子怎么不好使捏？……想当初，本老爷金榜题名时，数学可是得了满分，今天好歹要解决这个问题：
——人（系统！）挨板子（脉冲！）以后，会有什么表现（输出！）？
——费话，疼呗！
——我问的是：会有什么表现？
——看疼到啥程度。像这无赖的体格，每天挨一个板子啥事都不会有，连哼一下都不可能，你也看到他那得意洋洋的嘴脸了（输出0）；如果一次连揍他十个板子，他可能会皱皱眉头，咬咬牙，硬挺着不哼
（输出1）；揍到二十个板子，他会疼得脸部扭曲，象猪似地哼哼（输出3）；揍到三十个板子，他可能会象驴似地嚎叫，一把鼻涕一把泪地求你饶他一命（输出5）；揍到四十个板子，他会大小便失禁，勉
强哼出声来（输出1）；揍到五十个板子，他连哼一下都不可能（输出0）——死啦！
县令铺开坐标纸，以打板子的个数作为X轴，以哼哼的程度（输出）为Y轴，绘制了一条曲线：
——呜呼呀！这曲线象一座高山，弄不懂弄不懂。为啥那个无赖连挨了三十天大板却不喊绕命呀？
—— 呵呵，你打一次的时间间隔（Δτ=24小时）太长了，所以那个无赖承受的痛苦程度一天一利索，没有叠加，始终是一个常数；如果缩短打板子的时间间隔（建议 Δτ=0.5秒），那他的痛苦程度可就迅速叠加了；等到这无赖挨三十个大板（t=30）时，痛苦程度达到了他能喊叫的极限，会收到最好的惩戒效果，再多打就显示不出您的仁慈了。
——还是不太明白，时间间隔小，为什么痛苦程度会叠加呢？
——这与人（线性时不变系统）对板子（脉冲、输入、激励）的响应有关。什么是响应？人挨一个板子后，疼痛的感觉会在一天（假设的，因人而异）内慢慢消失（衰减），而不可能突然消失。这样一来，只要打板子的时间间隔很小，每一个板子引起的疼痛都来不及完全衰减，都会对最终的痛苦程度有不同的贡献：
t个大板子造成的痛苦程度=Σ(第τ个大板子引起的痛苦*衰减系数)
[衰减系数是（t-τ）的函数，仔细品味]
数学表达为：y(t)=∫T(τ)H(t-τ)
——拿人的痛苦来说卷积的事，太残忍了。除了人以外，其他事物也符合这条规律吗？
——呵呵，县令大人毕竟仁慈。其实除人之外，很多事情也遵循此道。好好想一想，铁丝为什么弯曲一次不折，快速弯曲多次却会轻易折掉呢？
——恩，一时还弄不清，容本官慢慢想来——但有一点是明确地——来人啊，将撒尿的那个无赖抓来，狠打40大板！
有一个七品县令，喜欢用打板子来惩戒那些市井无赖，而且有个惯例：如果没犯大罪，只打一板，释放回家，以示爱民如子。
有一个无赖，想出人头地却没啥指望，心想：既然扬不了善名，出恶名也成啊。怎么出恶名？炒作呗！怎么炒作？找名人呀！他自然想到了他的行政长官——县令。
无赖于是光天化日之下，站在县衙门前撒了一泡尿，后果是可想而知地，自然被请进大堂挨了一板子，然后昂首挺胸回家，躺了一天，嘿！身上啥事也没有！第二天如法炮制，全然不顾行政长管的仁慈和衙门的体面，第三天、第四天……每天去县衙门领一个板子回来，还喜气洋洋地，坚持一个月之久！这无赖的名气已经和衙门口的臭气一样，传遍八方了！
县令大人噤着鼻子，呆呆地盯着案子上的惊堂木，拧着眉头思考一个问题：这三十个大板子怎么不好使捏？……想当初，本老爷金榜题名时，数学可是得了满分，今天好歹要解决这个问题：
——人（系统！）挨板子（脉冲！）以后，会有什么表现（输出！）？
——费话，疼呗！
——我问的是：会有什么表现？
——看疼到啥程度。像这无赖的体格，每天挨一个板子啥事都不会有，连哼一下都不可能，你也看到他那得意洋洋的嘴脸了（输出0）；如果一次连揍他十个板子，他可能会皱皱眉头，咬咬牙，硬挺着不哼
（输出1）；揍到二十个板子，他会疼得脸部扭曲，象猪似地哼哼（输出3）；揍到三十个板子，他可能会象驴似地嚎叫，一把鼻涕一把泪地求你饶他一命（输出5）；揍到四十个板子，他会大小便失禁，勉
强哼出声来（输出1）；揍到五十个板子，他连哼一下都不可能（输出0）——死啦！
县令铺开坐标纸，以打板子的个数作为X轴，以哼哼的程度（输出）为Y轴，绘制了一条曲线：
——呜呼呀！这曲线象一座高山，弄不懂弄不懂。为啥那个无赖连挨了三十天大板却不喊绕命呀？
—— 呵呵，你打一次的时间间隔（Δτ=24小时）太长了，所以那个无赖承受的痛苦程度一天一利索，没有叠加，始终是一个常数；如果缩短打板子的时间间隔（建议 Δτ=0.5秒），那他的痛苦程度可就迅速叠加了；等到这无赖挨三十个大板（t=30）时，痛苦程度达到了他能喊叫的极限，会收到最好的惩戒效果，再多打就显示不出您的仁慈了。
——还是不太明白，时间间隔小，为什么痛苦程度会叠加呢？
——这与人（线性时不变系统）对板子（脉冲、输入、激励）的响应有关。什么是响应？人挨一个板子后，疼痛的感觉会在一天（假设的，因人而异）内慢慢消失（衰减），而不可能突然消失。这样一来，只要打板子的时间间隔很小，每一个板子引起的疼痛都来不及完全衰减，都会对最终的痛苦程度有不同的贡献：
t个大板子造成的痛苦程度=Σ(第τ个大板子引起的痛苦*衰减系数)
[衰减系数是（t-τ）的函数，仔细品味]
数学表达为：y(t)=∫T(τ)H(t-τ)
——拿人的痛苦来说卷积的事，太残忍了。除了人以外，其他事物也符合这条规律吗？
——呵呵，县令大人毕竟仁慈。其实除人之外，很多事情也遵循此道。好好想一想，铁丝为什么弯曲一次不折，快速弯曲多次却会轻易折掉呢？
——恩，一时还弄不清，容本官慢慢想来——但有一点是明确地——来人啊，将撒尿的那个无赖抓来，狠打40大板！
卷积及拉普拉斯变换的通俗解释–对于我这类没学过信号系统的人来说太需要了
卷积(convolution, 另一个通用名称是德文的Faltung)的名称由来，是在于当初定义它时，定义成 integ(f1(v)*f2(t-v))dv，积分区间在0到t之间。举个简单的例子，大家可以看到，为什么叫”卷积”了。比方说在(0，100)间积分，用简单的辛普生积分公式，积分区间分成100等分，那么看到的是f1(0)和f2(100)相乘，f1(1)和f2(99)相乘，f1(2)和f2 (98)相乘，……… 等等等等，就象是在坐标轴上回卷一样。所以人们就叫它”回卷积分”，或者”卷积”了。
为了理解”卷积”的物理意义，不妨将那个问题”相当于它的时域的信号与系统的单位脉冲响应的卷积”略作变化。这个变化纯粹是为了方便表达和理解，不影响任何其它方面。将这个问题表述成这样一个问题：一个信号通过一个系统，系统的响应是频率响应或波谱响应，且看如何理解卷积的物理意义。
假设信号函数为f, 响应函数为g。f不仅是时间的函数(信号时有时无)，还是频率的函数(就算在某一固定时刻，还有的地方大有的地方小)；g也是时间的函数(有时候有反应，有时候没反应)，同时也是频率的函数(不同的波长其响应程度不一样)。那我们要看某一时刻 t 的响应信号，该怎么办呢？
这就需要卷积了。
要看某一时刻 t 的响应信号，自然是看下面两点：
1。你信号来的时候正赶上人家”系统”的响应时间段吗？
2。就算赶上系统响应时间段，响应有多少？
响 应不响应主要是看 f 和 g 两个函数有没有交叠；响应强度的大小不仅取决于所给的信号的强弱，还取决于在某频率处对单位强度响应率。响应强度是信号强弱和对单位强度信号响应率的乘积。”交叠”体现在f(t1)和g(t-t1)上，g之所以是”(t-t1)”就是看两个函数错开多少。
由于 f 和 g 两个函数都有一定的带宽分布(假若不用开头提到的”表述变化”就是都有一定的时间带宽分布)，这个信号响应是在一定”范围”内广泛响应的。算总的响应信号，当然要把所有可能的响应加起来，实际上就是对所有可能t1积分了。积分范围虽然一般在负无穷到正无穷之间；但在没有信号或者没有响应的地方，积也是白积，结果是0，所以往往积分范围可以缩减。
这就是卷积及其物理意义啊。并成一句话来说，就是看一个时有时无(当然作为特例也可以永恒存在)的信号，跟一个响应函数在某一时刻有多大交叠。
*********拉普拉斯*********
拉普拉斯(1729-1827) 是法国数学家，天文学家，物理学家。他提出拉普拉斯变换(Laplace Transform) 的目的是想要解决他当时研究的牛顿引力场和太阳系的问题中涉及的积分微分方程。
拉普拉斯变换其实是一个数学上的简便算法；想要了解其”物理”意义 — 如果有的话 — 请看我举这样一个例子：
问题：请计算十万乘以一千万。
对于没学过指数的人，就只会直接相乘；对于学过指数的人，知道不过是把乘数和被乘数表达成指数形式后，两个指数相加就行了；如果要问究竟是多少，把指数转回来就是。
“拉 普拉斯变换” 就相当于上述例子中把数转换成”指数” 的过程；进行了拉普拉斯变换之后，复杂的微分方程(对应于上例中”复杂”的乘法) 就变成了简单的代数方程，就象上例中”复杂”的乘法变成了简单的加减法。再把简单的代数方程的解反变换回去(就象把指数重新转换会一般的数一样)，就解决了原来那个复杂的微分方程。
所以要说拉普拉斯变换真有” 物理意义”的话，其物理意义就相当于人们把一般的有理数用指数形式表达一样。
另外说两句题外话：
1 。拉普拉斯变换之所以现在在电路中广泛应有，根本原因是电路中也广泛涉及了微分方程。
2。拉普拉斯变换与Z变换当然有紧密联系；其本质区别在于拉氏变换处理的是时间上连续的问题，Z变换处理的是时间上分立的问题。
卷积(convolution, 另一个通用名称是德文的Faltung)的名称由来，是在于当初定义它时，定义成 integ(f1(v)*f2(t-v))dv，积分区间在0到t之间。举个简单的例子，大家可以看到，为什么叫”卷积”了。比方说在(0，100)间积分，用简单的辛普生积分公式，积分区间分成100等分，那么看到的是f1(0)和f2(100)相乘，f1(1)和f2(99)相乘，f1(2)和f2 (98)相乘，……… 等等等等，就象是在坐标轴上回卷一样。所以人们就叫它”回卷积分”，或者”卷积”了。
为了理解”卷积”的物理意义，不妨将那个问题”相当于它的时域的信号与系统的单位脉冲响应的卷积”略作变化。这个变化纯粹是为了方便表达和理解，不影响任何其它方面。将这个问题表述成这样一个问题：一个信号通过一个系统，系统的响应是频率响应或波谱响应，且看如何理解卷积的物理意义。
假设信号函数为f, 响应函数为g。f不仅是时间的函数(信号时有时无)，还是频率的函数(就算在某一固定时刻，还有的地方大有的地方小)；g也是时间的函数(有时候有反应，有时候没反应)，同时也是频率的函数(不同的波长其响应程度不一样)。那我们要看某一时刻 t 的响应信号，该怎么办呢？
这就需要卷积了。
要看某一时刻 t 的响应信号，自然是看下面两点：
1。你信号来的时候正赶上人家”系统”的响应时间段吗？
2。就算赶上系统响应时间段，响应有多少？
响 应不响应主要是看 f 和 g 两个函数有没有交叠；响应强度的大小不仅取决于所给的信号的强弱，还取决于在某频率处对单位强度响应率。响应强度是信号强弱和对单位强度信号响应率的乘积。”交叠”体现在f(t1)和g(t-t1)上，g之所以是”(t-t1)”就是看两个函数错开多少。
由于 f 和 g 两个函数都有一定的带宽分布(假若不用开头提到的”表述变化”就是都有一定的时间带宽分布)，这个信号响应是在一定”范围”内广泛响应的。算总的响应信号，当然要把所有可能的响应加起来，实际上就是对所有可能t1积分了。积分范围虽然一般在负无穷到正无穷之间；但在没有信号或者没有响应的地方，积也是白积，结果是0，所以往往积分范围可以缩减。
这就是卷积及其物理意义啊。并成一句话来说，就是看一个时有时无(当然作为特例也可以永恒存在)的信号，跟一个响应函数在某一时刻有多大交叠。
*********拉普拉斯*********
拉普拉斯(1729-1827) 是法国数学家，天文学家，物理学家。他提出拉普拉斯变换(Laplace Transform) 的目的是想要解决他当时研究的牛顿引力场和太阳系的问题中涉及的积分微分方程。
拉普拉斯变换其实是一个数学上的简便算法；想要了解其”物理”意义 — 如果有的话 — 请看我举这样一个例子：
问题：请计算十万乘以一千万。
对于没学过指数的人，就只会直接相乘；对于学过指数的人，知道不过是把乘数和被乘数表达成指数形式后，两个指数相加就行了；如果要问究竟是多少，把指数转回来就是。
“拉 普拉斯变换” 就相当于上述例子中把数转换成”指数” 的过程；进行了拉普拉斯变换之后，复杂的微分方程(对应于上例中”复杂”的乘法) 就变成了简单的代数方程，就象上例中”复杂”的乘法变成了简单的加减法。再把简单的代数方程的解反变换回去(就象把指数重新转换会一般的数一样)，就解决了原来那个复杂的微分方程。
所以要说拉普拉斯变换真有” 物理意义”的话，其物理意义就相当于人们把一般的有理数用指数形式表达一样。
另外说两句题外话：
1 。拉普拉斯变换之所以现在在电路中广泛应有，根本原因是电路中也广泛涉及了微分方程。
2。拉普拉斯变换与Z变换当然有紧密联系；其本质区别在于拉氏变换处理的是时间上连续的问题，Z变换处理的是时间上分立的问题。
Signals, Linear Systems, and Convolution
Download from here
Download from here
我们都知道卷积公式，但是它有什么物理意义呢？平时我们用卷积做过很多事情，信号处理时，输出函数是输入函数和系统函数的卷积；在图像处理时，两组幅分辨率不同的图卷积之后得到的互相平滑的图像可以方便处理。卷积甚至可以用在考试作弊中，为了让照片同时像两个人，只要把两人的图像卷积处理即可，这就是一种平滑的过程，可是我们怎么才能真正把公式和实际建立起一种联系呢？生活中就有实例：
卷积的物理意义？
在信号与系统中，两个函数所要表达的物理含义是什么？例如，一个系统，其单位冲激响应为h(t)，当输入信号为f(t)时，该系统的输出为y(t)。为什么y(t)是f(t)和h(t)的卷积？（从数学推导我明白，但其物理意义不明白。）y(t)是f(t)和h(t)的卷积表达了一个什么意思？
卷积(convolution, 另一个通用名称是德文的Faltung)的名称由来，是在于当初定义它时，定义成 integ(f1(v)*f2(t-v))dv，积分区间在0到t之间。举个简单的例子，大家可以看到，为什么叫“卷积”了。比方说在(0，100)间积分，用简单的辛普生积分公式，积分区间分成100等分，那么看到的是f1(0)和f2(100)相乘，f1(1)和f2(99)相乘，f1(2)和f2(98)相乘，......... 等等等等，就象是在坐标轴上回卷一样。所以人们就叫它“回卷积分”，或者“卷积”了。
为了理解“卷积”的物理意义，不妨将那个问题“相当于它的时域的信号与系统的单位脉冲响应的卷积”略作变化。这个变化纯粹是为了方便表达和理解，不影响任何其它方面。将这个问题表述成这样一个问题：一个信号通过一个系统，系统的响应是频率响应或波谱响应，且看如何理解卷积的物理意义。
假设信号函数为f, 响应函数为g。f不仅是时间的函数(信号时有时无)，还是频率的函数(就算在某一固定时刻，还有的地方大有的地方小)；g也是时间的函数(有时候有反应，有时候没反应)，同时也是频率的函数(不同的波长其响应程度不一样)。那我们要看某一时刻 t 的响应信号，该怎么办呢？
这就需要卷积了。
其实卷积积分应用广泛用在信号里面，一个是频域一个是时域
卷积是个啥？我忽然很想从本质上理解它。于是我从抽屉里翻出自己珍藏了许多年，每每下决心阅读却永远都读不完的《应用傅立叶变换》。
3.1 一维卷积的定义
函数f(x)与函数h(x)的卷积，由函参量的无穷积分
定义虽然找到了，但我还是一头雾水。卷积是个无穷积分吗？那它是干啥用的？再往后翻：几何说明、运算举例、基本性质，一堆的公式，就是没有说它是干啥用的。我于是坐在那呆想，忽然第二个困扰我的问题冒了出来：傅立叶变换是个啥？接着就是第三个、第四个、……、第N个问题。
傅立叶变换是个啥？听说能将时域上的东东变到频域上分析？哎？是变到频域上还是空间域上来着？到底啥是时域，频域，空间域？
上网查傅立叶变换的物理意义，没发现明确答案，倒发现了许多和我一样晕着问问题的人。结果又多出了许多名词，能量？功率谱？图像灰度域？……没办法又去翻那本教材。
1.1 一维傅立叶变换的定义与傅立叶积分定理
设f(x)是实变量x的函数，该函数可实可复，称积分
为函数f(x)的傅立叶变换。
吐血，啥是无穷积分来着？积分是啥来着？还能记起三角函数和差化积、积化和差公式吗？我忽然有种想把高中课本寻来重温的冲动。
卷积主要是为了将信号运算从时域转换为频域。
信号的时域的卷积等于频域的乘积。
利用这个性质以及特殊的δ函数可以通过抽样构造简单的调制电路
信号的时域的卷积等于频域的乘积。
利用这个性质以及特殊的δ函数可以通过抽样构造简单的调制电路
我比较赞同卷积的相关性的作用
匹配滤波器最简单的形式就是原信号反转移位相乘积分得到的近似＝相关
相关性越好得到的信号越强
还有解调中一些东西本质就是相关
匹配滤波器最简单的形式就是原信号反转移位相乘积分得到的近似＝相关
相关性越好得到的信号越强
还有解调中一些东西本质就是相关
卷积公式 解释 卷积公式是用来求随机变量和的密度函数(pdf)的计算公式。 定义式： z(t)=x(t)*y(t)= ∫x(m)y(t-m)dm. 已知x,y的pdf,x(t),y(t).现在要求z=x+y的pdf. 我们作变量替显，令 z=x+y,m=x. 雅可比行列式=1.那么,z，m联合密度就是f(z,m)=x(m)y(z-m)*1. 这样，就可以很容易求Z的在（z,m)中边缘分布 即fZ(z)=∫x(m)y(z-m)dm..... 由于这个公式和x(t),y(t)存在一一对应的关系。为了方便，所以记 ∫x(m)y(z-m)dm=x(t)*y(t) 长度为m的向量序列u和长度为n的向量序列v，卷积w的向量序列长度为(m+n-1), u(n)与v(n)的卷积w(n)定义为： w(n)=u(n)@v(n)=sum(v(m)*u(n-m)),m from 负无穷到正无穷； 当m=n时w(1) = u(1)*v(1) w(2) = u(1)*v(2)+u(2)*v(1) w(3) = u(1)*v(3)+u(2)*v(2)+u(3)*v(1) … w(n) = u(1)*v(n)+u(2)*v(n-1)+ … +u(n)*v(1) … w(2*n-1) = u(n)*v(n) 当m≠n时,应以0补齐阶次低的向量的高位后进行计算 这是数学中常用的一个公式，在概率论中，是个重点也是一个难点。
卷积公式是用来求随机变量和的密度函数(pdf)的计算公式。
定义式：
z(t)=x(t)*y(t)= ∫x(m)y(t-m)dm.
已知x,y的pdf,x(t),y(t).现在要求z=x+y的pdf. 我们作变量替显，令
z=x+y,m=x. 雅可比行列式=1.那么,t，m联合密度就是f(z,m)=x(m)y(z-m)*1. 这样，就可以很容易求Z的在（z,m)中边缘分布
即fZ(z)=∫x(m)y(z-m)dm..... 由于这个公式和x(t),y(t)存在一一对应的关系。为了方便，所以记 ∫x(m)y(z-m)dm=x(t)*y(t)
卷积是一种线性运算,图像处理中常见的mask运算都是卷积，广泛应用于图像滤波。castlman的书对卷积讲得很详细。
高斯变换就是用高斯函数对图像进行卷积。高斯算子可以直接从离散高斯函数得到：
for(i=0; i<N; i++)
{
for(j=0; j<N; j++)
{
g[i*N+j]=exp(-((i-(N-1)/2)^2+(j-(N-1)/2)^2))/(2*delta^2));
sum += g[i*N+j];
}
}
再除以 sum 得到归一化算子
N是滤波器的大小，delta自选
高斯变换就是用高斯函数对图像进行卷积。高斯算子可以直接从离散高斯函数得到：
for(i=0; i<N; i++)
{
for(j=0; j<N; j++)
{
g[i*N+j]=exp(-((i-(N-1)/2)^2+(j-(N-1)/2)^2))/(2*delta^2));
sum += g[i*N+j];
}
}
再除以 sum 得到归一化算子
N是滤波器的大小，delta自选
首先，再提到卷积之前，必须提到卷积出现的背景。卷积是在信号与线性系统的基础上或背景中出现的，脱离这个背景单独谈卷积是没有任何意义的，除了那个所谓褶反公式上的数学意义和积分（或求和，离散情况下）。
信号与线性系统，讨论的就是信号经过一个线性系统以后发生的变化（就是输入输出和所经过的所谓系统，这三者之间的数学关系）。所谓线性系统的含义，就是，这个所谓的系统，带来的输出信号与输入信号的数学关系式之间是线性的运算关系。
因此，实际上，都是要根据我们需要待处理的信号形式，来设计所谓的系统传递函数，那么这个系统的传递函数和输入信号，在数学上的形式就是所谓的卷积关系。
卷积关系最重要的一种情况，就是在信号与线性系统或数字信号处理中的卷积定理。利用该定理，可以将时间域或空间域中的卷积运算等价为频率域的相乘运算，从而利用FFT等快速算法，实现有效的计算，节省运算代价。
信号与线性系统，讨论的就是信号经过一个线性系统以后发生的变化（就是输入输出和所经过的所谓系统，这三者之间的数学关系）。所谓线性系统的含义，就是，这个所谓的系统，带来的输出信号与输入信号的数学关系式之间是线性的运算关系。
因此，实际上，都是要根据我们需要待处理的信号形式，来设计所谓的系统传递函数，那么这个系统的传递函数和输入信号，在数学上的形式就是所谓的卷积关系。
卷积关系最重要的一种情况，就是在信号与线性系统或数字信号处理中的卷积定理。利用该定理，可以将时间域或空间域中的卷积运算等价为频率域的相乘运算，从而利用FFT等快速算法，实现有效的计算，节省运算代价。
Deep Learning论文笔记之（四）CNN卷积神经网络推导和实现
自己平时看了一些论文，但老感觉看完过后就会慢慢的淡忘，某一天重新拾起来的时候又好像没有看过一样。所以想习惯地把一些感觉有用的论文中的知识点总结整理一下，一方面在整理过程中，自己的理解也会更深，另一方面也方便未来自己的勘察。更好的还可以放到博客上面与大家交流。因为基础有限，所以对论文的一些理解可能不太正确，还望大家不吝指正交流，谢谢。
本文的论文来自：
Notes on Convolutional Neural Networks, Jake Bouvrie。
这个主要是CNN的推导和实现的一些笔记，再看懂这个笔记之前，最好具有CNN的一些基础。这里也先列出一个资料供参考：
[1] Deep Learning（深度学习）学习笔记整理系列之（七）
[2] LeNet-5, convolutional neural networks
[3]卷积神经网络
[4] Neural Network for Recognition of Handwritten Digits
[5] Deep learning：三十八(Stacked CNN简单介绍)
[6] Gradient-based learning applied to document recognition.
[7]Imagenet classification with deep convolutional neural networks.
[8] UFLDL中的“卷积特征提取”和“池化”。
另外，这里有个matlab的Deep Learning的toolbox，里面包含了CNN的代码，在下一个博文中，我将会详细注释这个代码。这个笔记对这个代码的理解非常重要。
下面是自己对其中的一些知识点的理解：
《Notes on Convolutional Neural Networks》
一、介绍这个文档讨论的是CNNs的推导和实现。CNN架构的连接比权值要多很多，这实际上就隐含着实现了某种形式的规则化。这种特别的网络假定了我们希望通过数据驱动的方式学习到一些滤波器，作为提取输入的特征的一种方法。
本文中，我们先对训练全连接网络的经典BP算法做一个描述，然后推导2D CNN网络的卷积层和子采样层的BP权值更新方法。在推导过程中，我们更强调实现的效率，所以会给出一些Matlab代码。最后，我们转向讨论如何自动地学习组合前一层的特征maps，特别地，我们还学习特征maps的稀疏组合。
二、全连接的反向传播算法
典型的CNN中，开始几层都是卷积和下采样的交替，然后在最后一些层（靠近输出层的），都是全连接的一维网络。这时候我们已经将所有两维2D的特征maps转化为全连接的一维网络的输入。这样，当你准备好将最终的2D特征maps输入到1D网络中时，一个非常方便的方法就是把所有输出的特征maps连接成一个长的输入向量。然后我们回到BP算法的讨论。（更详细的基础推导可以参考UFLDL中“反向传导算法”）。
2.1、Feedforward Pass前向传播
在下面的推导中，我们采用平方误差代价函数。我们讨论的是多类问题，共c类，共N个训练样本。
表示第n个样本对应的标签的第k维。表示第n个样本对应的网络输出的第k个输出。对于多类问题，输出一般组织为“one-of-c”的形式，也就是只有该输入对应的类的输出节点输出为正，其他类的位或者节点为0或者负数，这个取决于你输出层的激活函数。sigmoid就是0，tanh就是-1.因为在全部训练集上的误差只是每个训练样本的误差的总和，所以这里我们先考虑对于一个样本的BP。对于第n个样本的误差，表示为：
2.2、Backpropagation Pass反向传播
反向传播回来的误差可以看做是每个神经元的基的灵敏度sensitivities（灵敏度的意思就是我们的基b变化多少，误差会变化多少，也就是误差对基的变化率，也就是导数了），定义如下：（第二个等号是根据求导的链式法则得到的）
公式（1）公式（2）三、Convolutional Neural Networks 卷积神经网络
3.1、Convolution Layers 卷积层
我们现在关注网络中卷积层的BP更新。在一个卷积层，上一层的特征maps被一个可学习的卷积核进行卷积，然后通过一个激活函数，就可以得到输出特征map。每一个输出map可能是组合卷积多个输入maps的值：
3.1.1、Computing the Gradients梯度计算
我们假定每个卷积层l都会接一个下采样层l+1 。对于BP来说，根据上文我们知道，要想求得层l的每个神经元对应的权值的权值更新，就需要先求层l的每一个神经节点的灵敏度δ（也就是权值更新的公式（2））。为了求这个灵敏度我们就需要先对下一层的节点（连接到当前层l的感兴趣节点的第l+1层的节点）的灵敏度求和（得到δl+1），然后乘以这些连接对应的权值（连接第l层感兴趣节点和第l+1层节点的权值）W。再乘以当前层l的该神经元节点的输入u的激活函数f的导数值（也就是那个灵敏度反向传播的公式（1）的δl的求解），这样就可以得到当前层l每个神经节点对应的灵敏度δl了。
然而，因为下采样的存在，采样层的一个像素（神经元节点）对应的灵敏度δ对应于卷积层（上一层）的输出map的一块像素（采样窗口大小）。因此，层l中的一个map的每个节点只与l+1层中相应map的一个节点连接。
为了有效计算层l的灵敏度，我们需要上采样upsample 这个下采样downsample层对应的灵敏度map（特征map中每个像素对应一个灵敏度，所以也组成一个map），这样才使得这个灵敏度map大小与卷积层的map大小一致，然后再将层l的map的激活值的偏导数与从第l+1层的上采样得到的灵敏度map逐元素相乘（也就是公式（1））。
在下采样层map的权值都取一个相同值β，而且是一个常数。所以我们只需要将上一个步骤得到的结果乘以一个β就可以完成第l层灵敏度δ的计算。
我们可以对卷积层中每一个特征map j重复相同的计算过程。但很明显需要匹配相应的子采样层的map（参考公式（1））：
公式（3）是中的在卷积的时候与逐元素相乘的patch，输出卷积map的(u, v)位置的值是由上一层的(u, v)位置的patch与卷积核k_ij逐元素相乘的结果。咋一看，好像我们需要煞费苦心地记住输出map（和对应的灵敏度map）每个像素对应于输入map的哪个patch。但实际上，在Matlab中，可以通过一个代码就实现。对于上面的公式，可以用Matlab的卷积函数来实现：
我们先对delta灵敏度map进行旋转，这样就可以进行互相关计算，而不是卷积（在卷积的数学定义中，特征矩阵（卷积核）在传递给conv2时需要先翻转（flipped）一下。也就是颠倒下特征矩阵的行和列）。然后把输出反旋转回来，这样我们在前向传播进行卷积的时候，卷积核才是我们想要的方向。
3.2、Sub-sampling Layers 子采样层
对于子采样层来说，有N个输入maps，就有N个输出maps，只是每个输出map都变小了。
3.2.1、Computing the Gradients 梯度计算
这里最困难的是计算灵敏度map。一旦我们得到这个了，那我们唯一需要更新的偏置参数β和b就可以轻而易举了（公式（3））。如果下一个卷积层与这个子采样层是全连接的，那么就可以通过BP来计算子采样层的灵敏度maps。
我们需要计算卷积核的梯度，所以我们必须找到输入map中哪个patch对应输出map的哪个像素。这里，就是必须找到当前层的灵敏度map中哪个patch对应与下一层的灵敏度map的给定像素，这样才可以利用公式（1）那样的δ递推，也就是灵敏度反向传播回来。另外，需要乘以输入patch与输出像素之间连接的权值，这个权值实际上就是卷积核的权值（已旋转的）。
到这里，我们就可以对b和β计算梯度了。首先，加性基b的计算和上面卷积层的一样，对灵敏度map中所有元素加起来就可以了：
3.3、Learning Combinations of Feature Maps 学习特征map的组合
大部分时候，通过卷积多个输入maps，然后再对这些卷积值求和得到一个输出map，这样的效果往往是比较好的。在一些文献中，一般是人工选择哪些输入maps去组合得到一个输出map。但我们这里尝试去让CNN在训练的过程中学习这些组合，也就是让网络自己学习挑选哪些输入maps来计算得到输出map才是最好的。我们用αij表示在得到第j个输出map的其中第i个输入map的权值或者贡献。这样，第j个输出map可以表示为：
Softmax函数的导数表示为：
3.3.1、Enforcing Sparse Combinations 加强稀疏性组合
为了限制αi是稀疏的，也就是限制一个输出map只与某些而不是全部的输入maps相连。我们在整体代价函数里增加稀疏约束项Ω(α)。对于单个样本，重写代价函数为：
3.4、Making it Fast with MATLAB
CNN的训练主要是在卷积层和子采样层的交互上，其主要的计算瓶颈是：
1）前向传播过程：下采样每个卷积层的maps；
2）反向传播过程：上采样高层子采样层的灵敏度map，以匹配底层的卷积层输出maps的大小；
3）sigmoid的运用和求导。
对于第一和第二个问题，我们考虑的是如何用Matlab内置的图像处理函数去实现上采样和下采样的操作。对于上采样，imresize函数可以搞定，但需要很大的开销。一个比较快速的版本是使用Kronecker乘积函数kron。通过一个全一矩阵ones来和我们需要上采样的矩阵进行Kronecker乘积，就可以实现上采样的效果。对于前向传播过程中的下采样，imresize并没有提供在缩小图像的过程中还计算nxn块内像素的和的功能，所以没法用。一个比较好和快速的方法是用一个全一的卷积核来卷积图像，然后简单的通过标准的索引方法来采样最后卷积结果。例如，如果下采样的域是2x2的，那么我们可以用2x2的元素全是1的卷积核来卷积图像。然后再卷积后的图像中，我们每个2个点采集一次数据，y=x(1:2:end,1:2:end)，这样就可以得到了两倍下采样，同时执行求和的效果。
对于第三个问题，实际上有些人以为Matlab中对sigmoid函数进行inline的定义会更快，其实不然，Matlab与C/C++等等语言不一样，Matlab的inline反而比普通的函数定义更非时间。所以，我们可以直接在代码中使用计算sigmoid函数及其导数的真实代码。
版权声明：本文为博主原创文章，未经博主允许不得转载。
◇◇新语丝(www.xys.org)(xys.dxiong.com)(xys.dropin.org)(xys-reader.org)◇◇
人类随想——自私基因的生存机器
作者：太簇
人类一直自视颇高。在日心说出现之前，人类认为自己居住的地球是太阳系
的中心。在进化论出现之前，人类认为自己是造物主着意创造出来主宰世界的，
是万物之灵，与其它动物有本质区别，所以才有“禽兽不如”之类骂人的话。在
社会生物学被接受为理解人类行为的科学基础之前，人类认为自己的思想、行为、
道德、文化等是无法用自然科学的方法研究的——即便到了现在，仍有人文学者
顽固地抵抗着科学方法的侵入，并挥舞着“科学主义”的大帽子扣在任何一个试
图用科学方法研究人文的人的头上。中华民族的祖先，在这方面也不落后于任何
其它民族。中国的“中”字就赤裸裸地暴露了自以为世界中心的狭隘的自信与偏
见。这狭隘扩展开去，就是用“鬼子”称呼异族人，以及当今仍然泛滥的认为可
以有中国特色的科学或医学的想法。
中华民族与世界所有其他民族的这种自大自恋心理，其实有更深层的生物根
源——那就是，人类做为一个物种，象地球上所有其它生命一样，不过是自私的
基因的生存机器。自私的基因驱使着我们本能地以自我为中心，最大限度地保护
自己和获得生存资源，以保证生存质量，最终完成自私的基因赋予我们的复制使
命。
从地球上出现生命至今，已有36亿年。生命进化之树自此生根发芽，伸枝吐
杈，茁壮成长，直至大约50万年前，早期人类出现。在大约13万年前，现代人类
走出非洲，散向各个适合人类居住的世界角落。千山万水和十余万年的隔离，并
没有把我们人类分成几个不同的物种。但长久的地理上的隔离，使得我们这些拥
有共同祖先的后代彼此生疏了，用不具有生物学意义的所谓种族或民族画地为牢、
自设樊篱，出现了“非我族类，其心必异”或者“鬼子”之类的说法。
现代科技改变了这种危险狭隘的趋势。今日，我们乘喷气式客机，在一天之
内可以跨越任何天然障碍，到达地球任何一个角落。各个“种族”的人类相互通
商、文化交流，通过移民到另外一片大陆上安居生息，乃至通婚，使得“种族”
逐渐成了一个历史概念。在“种族”大融合上，美国做为一个移民国家，做得最
好。美国在经济文化上的成功，其实是世界各族人民的共同成果。美国向我们展
示了“种族”融合不仅可能，而且对人类的共同进步与发展可以有重大的促进作
用。那些夜郎自大的所谓纯正“种族”，在今天世界上的地位并不高。
现代科技还向我们揭示了，做为30多亿年进化的产物之一，人类是一架多么
精巧的生存机器，以及我们的生存环境对这架机器今天拥有的结构与功能起了怎
样的塑造作用。
空气与水，是我们生命之必须。停止呼吸空气，我们几分钟内就会死亡。没
有水，我们会在一星期左右离开这个世界。令人惊奇的是，这两种对我们生命如
此重要的物质，竟是无嗅无味的。说它们无嗅无味，当然是相对我们的感官而言。
我们能闻到香味臭味，能尝到酸甜苦辣咸鲜，但却对空气和水无动于衷。为什么
我们的感官没有进化出对空气和水的嗅味觉呢？为解答这个问题，我们可以逆向
思维一下：假如空气和水可以给我们的嗅觉味觉以一定程度的刺激，会发生什么
事儿呢？
我们会很悲惨！我们所谓的味觉嗅觉，是我们舌头上和鼻腔粘膜上的感受器
捕捉到了某些特定的分子，触发了神经脉冲；神经脉冲经神经纤维传导至大脑，
触发更多的神经元，产生了感觉——说通俗点，就是放电。如果空气和水能被我
们的嗅味觉器官感知到，那我们的嗅味觉神经通道会永久地处于“放电状态”！
那感觉就像被终身监禁在一个充溢着同一种香水味或臭鸡蛋味的牢房里，永世不
得放风，生不如死。
对空气和水有嗅味觉，如上所述，是有进化劣势的。而对空气和水无嗅味觉，
除了让我们不受持久神经放电的折磨外，还可以有其它的进化优势，那就是对空
气和水的大部分污染，我们马上就可以靠嗅味觉察觉到，从而逃避危害。洁净的
空气和水，就像一张洁白无暇的画纸，在其上的任何油彩都会被轻易发现。
水占了人体体重的62%左右。人体的细胞其实就是一个个被细胞膜包起来以
水为主要成分的液体环境，在其中进行着各种各样维持生命的物理化学过程。我
们的眼睛中，晶状体后面的玻璃体占了绝大部分的体积。玻璃体的主要成分，便
是水。我们知道，眼睛的功能是感受光线，而地球上的光线，主要由太阳来。太
阳光如我们的手机信号和互联网上时刻在奔流的数字信号一样，都是电磁波。太
阳光的波长范围大概从150纳米到2、3000纳米，其中400纳米到700纳米一段为最
强，500纳米（绿光）处为峰值。太阳光经反射折射后，进入我们的眼睛，穿越
玻璃体，到达视网膜，被接收和转化为视觉神经信号。物理学告诉我们，光线在
液体中穿行时，强度要衰减，或者说亮度要变暗；在以水为主要成分的玻璃体中
穿行，也不例外。物理学还告诉我们，水这种液体，在衰减或吸收太阳光时，并
不是对所有波长（或颜色）都一视同仁的。对太阳光的亮度最强的波长范围
（400纳米到700纳米），水的吸收反而最少！
这是很有趣的一个事实：太阳光最强的一段颜色，正是水吸收最少的一段，
也正是——鼓点敲起——我们人类能感知到一段阳光——可见光。如果说太阳最
强的波段与水吸收最弱的波段重合，是个巧合的话，那么我们人类偏偏来感知这
一波段，就不是巧合了。这应该是进化这个盲目的钟表匠的又一个杰作——感知
这一段是最省事的，从利用光源的强度分布到感光器官眼睛的内部材料选择，均
是如此。
还有一个很有趣的巧合：太阳光谱中亮度峰值的波长，如上所说，在500纳
米（也即绿光处）左右；而水吸收曲线的谷底，也恰巧是500纳米左右；人眼中
主要用来感受弱光的柱状细胞，对505纳米的光最敏感。前两者当然还是巧合，
但柱状细胞的的感光波长峰值与它们的吻合，应该还是进化的产物。
说到绿色，没有很多物理学知识的朋友会联想到郁郁葱葱的草地和茂密的森
林。人类对绿色有一种天然的喜好，认为它是生命的象征。在初春，看到小草发
芽，树木吐绿，生活在温带的人类摆脱了漫长冬天的压抑，心情也会象小草绿树
一样，充满了生机。这并不完全是个文学的比喻，而更是揭示了人类的动物本性，
因为在我们的祖先还远未进化为现代人的时候，我们就依赖草地树木，从中得到
食物，包括草食动物和果实。绿色，就意味着食物、生命。没有现代科学知识，
我们的祖先当然不知道，我们须臾不能停止的呼吸，也与这绿色息息相关。绿色
的植物、我们、空气、水以及土壤，构成了一个可持续发展的稳定生态圈。在这
个生物圈里，茂盛的树木和葱葱的小草的根深扎在坚实的土壤里，吸吮着那里的
水和养分。树叶、草叶吸收着由距我们1亿五千万公里远的一座天然核电站发射
的电磁波和空气里的二氧化碳，释放出氧气——那可以使我们血红细胞重新变得
鲜红、令我们体内的发电站运转的生命分子。满眼悦目的绿色，我的科学脑袋告
诉我，实际上是生命的弃色——被叶片中的叶绿素排斥掉的颜色。做为进化产物
的人类眼睛最敏感最愉悦的颜色，竟是被光合作用排斥掉的弃物，而同时由光合
作用释放出的废气，又竟是人类不可离弃的生命之气。
这个认识给我带来的愉悦，比哲学、文学、宗教都要深沉、宏大。
人类随想——自私基因的生存机器
作者：太簇
人类一直自视颇高。在日心说出现之前，人类认为自己居住的地球是太阳系
的中心。在进化论出现之前，人类认为自己是造物主着意创造出来主宰世界的，
是万物之灵，与其它动物有本质区别，所以才有“禽兽不如”之类骂人的话。在
社会生物学被接受为理解人类行为的科学基础之前，人类认为自己的思想、行为、
道德、文化等是无法用自然科学的方法研究的——即便到了现在，仍有人文学者
顽固地抵抗着科学方法的侵入，并挥舞着“科学主义”的大帽子扣在任何一个试
图用科学方法研究人文的人的头上。中华民族的祖先，在这方面也不落后于任何
其它民族。中国的“中”字就赤裸裸地暴露了自以为世界中心的狭隘的自信与偏
见。这狭隘扩展开去，就是用“鬼子”称呼异族人，以及当今仍然泛滥的认为可
以有中国特色的科学或医学的想法。
中华民族与世界所有其他民族的这种自大自恋心理，其实有更深层的生物根
源——那就是，人类做为一个物种，象地球上所有其它生命一样，不过是自私的
基因的生存机器。自私的基因驱使着我们本能地以自我为中心，最大限度地保护
自己和获得生存资源，以保证生存质量，最终完成自私的基因赋予我们的复制使
命。
从地球上出现生命至今，已有36亿年。生命进化之树自此生根发芽，伸枝吐
杈，茁壮成长，直至大约50万年前，早期人类出现。在大约13万年前，现代人类
走出非洲，散向各个适合人类居住的世界角落。千山万水和十余万年的隔离，并
没有把我们人类分成几个不同的物种。但长久的地理上的隔离，使得我们这些拥
有共同祖先的后代彼此生疏了，用不具有生物学意义的所谓种族或民族画地为牢、
自设樊篱，出现了“非我族类，其心必异”或者“鬼子”之类的说法。
现代科技改变了这种危险狭隘的趋势。今日，我们乘喷气式客机，在一天之
内可以跨越任何天然障碍，到达地球任何一个角落。各个“种族”的人类相互通
商、文化交流，通过移民到另外一片大陆上安居生息，乃至通婚，使得“种族”
逐渐成了一个历史概念。在“种族”大融合上，美国做为一个移民国家，做得最
好。美国在经济文化上的成功，其实是世界各族人民的共同成果。美国向我们展
示了“种族”融合不仅可能，而且对人类的共同进步与发展可以有重大的促进作
用。那些夜郎自大的所谓纯正“种族”，在今天世界上的地位并不高。
现代科技还向我们揭示了，做为30多亿年进化的产物之一，人类是一架多么
精巧的生存机器，以及我们的生存环境对这架机器今天拥有的结构与功能起了怎
样的塑造作用。
空气与水，是我们生命之必须。停止呼吸空气，我们几分钟内就会死亡。没
有水，我们会在一星期左右离开这个世界。令人惊奇的是，这两种对我们生命如
此重要的物质，竟是无嗅无味的。说它们无嗅无味，当然是相对我们的感官而言。
我们能闻到香味臭味，能尝到酸甜苦辣咸鲜，但却对空气和水无动于衷。为什么
我们的感官没有进化出对空气和水的嗅味觉呢？为解答这个问题，我们可以逆向
思维一下：假如空气和水可以给我们的嗅觉味觉以一定程度的刺激，会发生什么
事儿呢？
我们会很悲惨！我们所谓的味觉嗅觉，是我们舌头上和鼻腔粘膜上的感受器
捕捉到了某些特定的分子，触发了神经脉冲；神经脉冲经神经纤维传导至大脑，
触发更多的神经元，产生了感觉——说通俗点，就是放电。如果空气和水能被我
们的嗅味觉器官感知到，那我们的嗅味觉神经通道会永久地处于“放电状态”！
那感觉就像被终身监禁在一个充溢着同一种香水味或臭鸡蛋味的牢房里，永世不
得放风，生不如死。
对空气和水有嗅味觉，如上所述，是有进化劣势的。而对空气和水无嗅味觉，
除了让我们不受持久神经放电的折磨外，还可以有其它的进化优势，那就是对空
气和水的大部分污染，我们马上就可以靠嗅味觉察觉到，从而逃避危害。洁净的
空气和水，就像一张洁白无暇的画纸，在其上的任何油彩都会被轻易发现。
水占了人体体重的62%左右。人体的细胞其实就是一个个被细胞膜包起来以
水为主要成分的液体环境，在其中进行着各种各样维持生命的物理化学过程。我
们的眼睛中，晶状体后面的玻璃体占了绝大部分的体积。玻璃体的主要成分，便
是水。我们知道，眼睛的功能是感受光线，而地球上的光线，主要由太阳来。太
阳光如我们的手机信号和互联网上时刻在奔流的数字信号一样，都是电磁波。太
阳光的波长范围大概从150纳米到2、3000纳米，其中400纳米到700纳米一段为最
强，500纳米（绿光）处为峰值。太阳光经反射折射后，进入我们的眼睛，穿越
玻璃体，到达视网膜，被接收和转化为视觉神经信号。物理学告诉我们，光线在
液体中穿行时，强度要衰减，或者说亮度要变暗；在以水为主要成分的玻璃体中
穿行，也不例外。物理学还告诉我们，水这种液体，在衰减或吸收太阳光时，并
不是对所有波长（或颜色）都一视同仁的。对太阳光的亮度最强的波长范围
（400纳米到700纳米），水的吸收反而最少！
这是很有趣的一个事实：太阳光最强的一段颜色，正是水吸收最少的一段，
也正是——鼓点敲起——我们人类能感知到一段阳光——可见光。如果说太阳最
强的波段与水吸收最弱的波段重合，是个巧合的话，那么我们人类偏偏来感知这
一波段，就不是巧合了。这应该是进化这个盲目的钟表匠的又一个杰作——感知
这一段是最省事的，从利用光源的强度分布到感光器官眼睛的内部材料选择，均
是如此。
还有一个很有趣的巧合：太阳光谱中亮度峰值的波长，如上所说，在500纳
米（也即绿光处）左右；而水吸收曲线的谷底，也恰巧是500纳米左右；人眼中
主要用来感受弱光的柱状细胞，对505纳米的光最敏感。前两者当然还是巧合，
但柱状细胞的的感光波长峰值与它们的吻合，应该还是进化的产物。
说到绿色，没有很多物理学知识的朋友会联想到郁郁葱葱的草地和茂密的森
林。人类对绿色有一种天然的喜好，认为它是生命的象征。在初春，看到小草发
芽，树木吐绿，生活在温带的人类摆脱了漫长冬天的压抑，心情也会象小草绿树
一样，充满了生机。这并不完全是个文学的比喻，而更是揭示了人类的动物本性，
因为在我们的祖先还远未进化为现代人的时候，我们就依赖草地树木，从中得到
食物，包括草食动物和果实。绿色，就意味着食物、生命。没有现代科学知识，
我们的祖先当然不知道，我们须臾不能停止的呼吸，也与这绿色息息相关。绿色
的植物、我们、空气、水以及土壤，构成了一个可持续发展的稳定生态圈。在这
个生物圈里，茂盛的树木和葱葱的小草的根深扎在坚实的土壤里，吸吮着那里的
水和养分。树叶、草叶吸收着由距我们1亿五千万公里远的一座天然核电站发射
的电磁波和空气里的二氧化碳，释放出氧气——那可以使我们血红细胞重新变得
鲜红、令我们体内的发电站运转的生命分子。满眼悦目的绿色，我的科学脑袋告
诉我，实际上是生命的弃色——被叶片中的叶绿素排斥掉的颜色。做为进化产物
的人类眼睛最敏感最愉悦的颜色，竟是被光合作用排斥掉的弃物，而同时由光合
作用释放出的废气，又竟是人类不可离弃的生命之气。
这个认识给我带来的愉悦，比哲学、文学、宗教都要深沉、宏大。
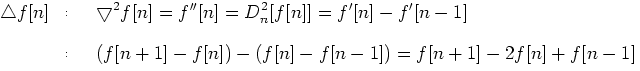
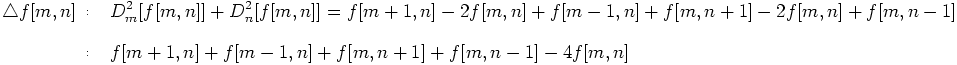
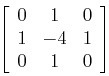
No comments:
Post a Comment