1、数学发展简史:初等数学; - 佛山科学技术学院
Talk:Minkowski space - Wikipedia, the free encyclopedia
... only works in complex Minkowski space. Affine space was essential to Minkowski's 2nd presentation (the 'Space and Time' one usual nowadays) because he ...
What happens when light hits light? | Page 2 - Physics Forums
www.physicsforums.com › Physics › General Physics
Dec 31, 2012 - ... from the book of feynman lectures itself.I don't know what you mean by linear space here.Some vector space,minkowski space,affine space?The 2-dimensional plane, well-known from elementary Euclidean geometry, is an example of an affine space. Remember that in elementary geometry none of the points in the plane is special—there is no origin. A real n-dimensional affine space is distinguished from the vector space
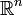 by having no special point, no fixed origin.[1]
by having no special point, no fixed origin.[1] From elementary geometry we know that any two points in a plane (a collection of infinitely many points) can be connected by a line segment. If the points P and Q in a plane are ordered with P before Q, the line segment connecting the two becomes an arrow pointing from P to Q. This arrow can be mapped onto a vector, the difference vector, denoted by
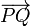 .[2] If all arrows in a plane can be mapped onto vectors of a 2-dimensional vector space V2, called the difference space, the plane is an affine space of dimension 2, denoted by A2. Arrows that are mapped onto the same vector in the difference space are said to be parallel, they differ from each other by translation.
.[2] If all arrows in a plane can be mapped onto vectors of a 2-dimensional vector space V2, called the difference space, the plane is an affine space of dimension 2, denoted by A2. Arrows that are mapped onto the same vector in the difference space are said to be parallel, they differ from each other by translation. In elementary analytic geometry, the map of arrows onto vectors is almost always defined by the choice of an origin O, which is a point somewhere in the plane. Clearly, an arbitrary point P is the head of an arrow with tail in the origin and corresponding with the unique difference vector
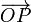 . All arrows with tail in O are mapped one-to-one onto a 2-dimensional difference space V2, with the vector addition in V2 in one-to-one correspondence with the parallelogram rule for the addition of arrows in the plane.
. All arrows with tail in O are mapped one-to-one onto a 2-dimensional difference space V2, with the vector addition in V2 in one-to-one correspondence with the parallelogram rule for the addition of arrows in the plane. Usually one equips the difference space with an inner product, turning it into an inner product space. Its elements have well-defined length, namely, the square root of the inner product of the vector with itself. The distance between any two points P and Q may now be defined as the length of
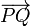 in V2. A two-dimensional affine space, with this distance defined between the points, is the Euclidean plane known from high-school geometry.
in V2. A two-dimensional affine space, with this distance defined between the points, is the Euclidean plane known from high-school geometry. Upon formalizing and generalizing the definition of an affine space, we replace the dimension 2 by an arbitrary finite dimension n and replace arrows by ordered pairs of points ("head" and "tail") in a given point space A. Briefly, A is an affine space of dimension n if there exists a map of the Cartesian product, A × A onto a vector space of dimension n. This map must satisfy certain axioms that are treated in the next section. If the dimension needs to be exhibited, we may write An for the affine space of dimension n.
[相對論]十九、向量與張量的協變微分、向量平移、聯絡
臺大科學教育發展中心 影音平台 .NTU CAStudio
当问题涉及空间中无限多个方向时,将它们用固定球面上的点来表示是有利益的。这些点是该球面上与这些方向平行的半径的端点。这一从属球面(auxiliary sphere)的球心和半径可以任取,比如半径可选为单位长。这与天文学中常用的做法不约而同,在那里,所有方向由一个设想的半径无穷大的球形天体上的点表示。从而球面三角学以及其它一些定理(其中包含作者得到的一个利用很广的定理)可以用来处置涉及不同方向上几何量比拟的问题。
如果我们用上述办法来表示球面上各点的法方向,即:曲面上任一点对应于附属球面上一点,则一般地,曲面上的一条曲线将对应从属球面上一条曲线;曲面的一部分对应附属球面的一部分,并且曲面这一部分和平面差异越小时,附属球面上相应的面积就越小。由此,一个十分自然的设法是以附属球面上相应部份的面积作为曲面给定部分的全曲率的度量。因而作者称它为曲面上该部分的总曲率。
当问题涉及空间中无限多个方向时,将它们用固定球面上的点来表示是有利益的。这些点是该球面上与这些方向平行的半径的端点。这一从属球面(auxiliary sphere)的球心和半径可以任取,比如半径可选为单位长。这与天文学中常用的做法不约而同,在那里,所有方向由一个设想的半径无穷大的球形天体上的点表示。从而球面三角学以及其它一些定理(其中包含作者得到的一个利用很广的定理)可以用来处置涉及不同方向上几何量比拟的问题。
如果我们用上述办法来表示球面上各点的法方向,即:曲面上任一点对应于附属球面上一点,则一般地,曲面上的一条曲线将对应从属球面上一条曲线;曲面的一部分对应附属球面的一部分,并且曲面这一部分和平面差异越小时,附属球面上相应的面积就越小。由此,一个十分自然的设法是以附属球面上相应部份的面积作为曲面给定部分的全曲率的度量。因而作者称它为曲面上该部分的总曲率。
Nature of spacetime 4-vector and tangent space?
An entry level confusion about spacetime. I understand that a 4-vector describes a point or event in spacetime. But I've also read (Bertschinger, 1999) that re spacetime "we are discussing tangent vectors that lie in the tangent space of the manifold at each point". If a point/event is described by a single 4-vector, what are all these tangent vectors that lie on the same point? Do they have different co-ordinates to the 'point/event' 4-vector? Could I also ask how a 4-vector 'contains' any sense of direction (I'm thinking here of a vector having direction and magnitude)?
| |||
Your confusion comes from the difference between special and general relativity. In special relativity, the space-time manifold is assumed to carry the structure of 4-dimensional Minkowski space, which has the nice property that it is canonically identified with its own tangent space at the origin (since it is a vector space). So in special relativity you can speak of a space-time event as a 4-vector, and you can also speak of global Lorentz transformations (by doing the local Lorentz transformation in the tangent space and propagating the transformation to the whole space-time using the canonical identification).
In general relativity, however, the space-time is allowed to be an arbitrary Lorentzian manifold (what we do is break the global Lorentz symmetry of Minkowski space and require it to only hold infinitesimally, i.e. on the tangent space), and you don't have a canonical way of identifying the entire space-time with the tangent space of a fixed point. Therefore you cannot speak of a space-time event (now just a point in your space-time manifold) as a 4-vector! Edit Let me try to make the difference between an affine and non-affine space more apparent. Let us start by considering a two dimensional manifold. In fact, we'll just compare the usual flat plane and the sphere. On the plane, we can fix an arbitrary point and call it the origin. Starting from this origin, pick a direction, and call it the
On the sphere, however, you can again fix an arbitrary point and call it the "origin", and a direction which we call "
Now, going back to the plane, if instead you start by going "face But on the sphere, if you start by "face What does this mean? On a flat plane, from the above demonstration, after fixing an origin and a direction On the surface of the sphere (a curved manifold), however, the above example shows that the intuition we learned from studying classical mechanics about using vector addition for the "displacement vector" cannot hold for the positions of points. So you shouldn't think about space-time events in general relativity (which is a point on some possibly curved manifold), as vectors relative to a fixed origin. (Because with vectors you would be tempted to add them and so forth.) | |||||||||||||||||||||
|
Think of a liquid that is flowing in two dimensions on a flat surface. At every point we can draw a vector that points in the direction that the fluid is flowing in at that point. That is a vector in the vector space at that point, the tangent space. There is a tangent space at every point, because at every point the fluid could be flowing in any direction, although an equation of motion might require, for example, continuity from point to point. An example of a vector flow (found through Google images for "fluid flow") is http://www.dstu.univ-montp2.fr/geofracnet/Images/connollyflownet2.jpg. Graphically, of course, the tangent vectors to the flow can only be displayed at a finite number of points, but from the point of view of a differential equation there's a flow vector at every point. All the tangent spaces are exactly the same as all the others.
The "vectors" used to describe the points are vectors in the vector space at one particular point, the center of the coordinate system, with the vector describing the location of the other point relative to the center of the coordinate system as distances in two directions that aren't parallel. The four-dimensional case is no different provided we concern ourselves only with vector spaces, but the idea of a Lorentzian distance is of course different from the idea of a Euclidean distance. In coordinate terms, we could talk of two functions, A vector in 2 or in 4 dimensions can of course represent something other than a velocity field. In due course you will get straight what can be represented by vectors and what requires tensors. Now imagine a fluid flowing on the surface of a sphere. Again there is a tangent space at every point on the surface of the sphere, and all the tangent spaces are exactly the same as the others, but now it's harder to describe explicitly the way in which the many tangent spaces are the same as each other. Saying which point is which by using vectors in a tangent space at a specific point is also more problematic. | |||||||||||||
|
三民網路書店>X射線脈衝星導航系統原理與方法(簡體書)-帥平
www.m.sanmin.com.tw/Product/Index/001060483
2.1.1 矢量空間、歐氏空間和仿射空間的內涵 2.1.2 矢量的代數 ... 2.2.6 仿射空間的測地線微分方程 2.3 黎曼空間 ... 2.4 狹義相對論與廣義相對論的基本概念 2.4.1 牛頓 ...广义相对论_第3章_0x94文档库
www.0x94.com/doc/0tsXLuzUHoQ2mgRA8.html - 轉為繁體網頁
狭义相对论的四维Minkowski时空中,最常用的一种坐标变换就是代表惯性系之 ... 本章我们将在仿射空间中建立张量的定义和运算,并利用它来讨论空间的几何性质。引力論: - 第 191 頁 - Google 圖書結果
https://books.google.com.hk/books?isbn=9570911336 - 轉為繁體網頁
1997 - Astrophysics
一種是從狹義相對論度 ... Schild 的論證已經指出(沒有直接應用等效原理) ,狹義