偏微分方程的数值解
直线数值方法
引言
直线数值方法是一种求解偏微分方程的方法,它是通过将问题在除一个方向外的所有方向上离散化,并将该半离散问题作为常微分方程组或微分代数方程组进行积分来实现. 该方法的一个显著优点是,它可利用针对常微分方程和微分代数方程已经开发的成熟的一般用途方法和软件的优点来求解. 对于可用直线方法求解的偏微分方程,通常可以证明该方法是非常高效的.
偏微分方程问题必须在至少一个方向上是适定的初始值(柯西)的问题,因为所用的常微分方程和微分代数方程积分程序是初识值问题求解器. 这就排除了纯椭圆方程,如拉普拉斯方程等,但留下了一大类演化方程,可以相当有效地加以解决.
一个简单的例子可以更好地说明该方法的基本思想. 考虑下面的问题(一个土壤热量随季节变化的简单模型):
这个问题可用直线方法求解,因为存在初识值
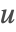
.
问题(1)将使用二阶有限差分,尤其利用了下面的逼近,对变量

进行离散化:
尽管有限差分离散是最常见的,但对于直线方法进行的离散并不一定要求用有限差分完成;有限体积甚至是有限元离散也可以使用.
要使用刚介绍的离散方法,选择一个均匀网格

,间距为
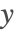
,使得
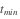
. 令

为

的值. 为了演示问题的建立,选定了
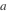
的一个特别值.
这里定义

的一个特别值,以及接下来的命令中用到的
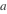
的对应值. 这可以改变,以进行更精细或更粗糙的空间逼近.
定义
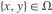
的向量.
| Out[2]= |  |
对于
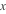
,可以使用中心的差公式(2),以获取一个常微分方程组. 但是,在这样做之前,纳入边界条件是非常有用的.
在

处的狄利克雷边界条件可以通过将

简单定义为

的函数来轻松处理. 另一种方法是将边界条件对时间进行微分,并把其加入边界条件. 这个例子将使用后一种方法.
在

处的 Neumann 边界条件稍微有点复杂. 关于二阶差分,一个处置这种问题的方法是通过反射:设想在区间

上使用在

和

处相同的边界条件对问题求解. 由于初始条件和边界条件关于

对称,解应该始终关于

对称,因此对称性质与在

处的 Neumann 边界条件等价. 因此

,

.
| Out[4]= | 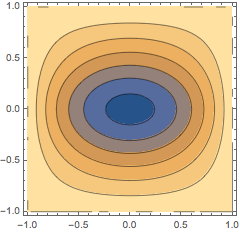 |
| Out[4]= | 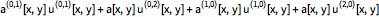 |
现在偏微分方程已部分离散成常微分方程初值问题,可以在
NDSolve 中通过常微分方程积分程序求解.
| Out[5]= | 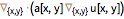 |
| Out[7]= | 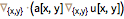 |
该图形暗示出将这种方法称作数值"直线方法"的原因.
直线之间的解可以通过插值法找到. 当
NDSolve 计算偏微分方程的解时,结果是一个二维
InterpolatingFunction.
| Out[7]= | 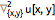 |
| Out[8]= |  |
所用设置

并没有给出一个非常准确的解. 当
NDSolve 计算解时,它使用初始条件下的空间误差估计来确定网格间距. 时间(或至少是类时间)变量的误差通过自适应常微分方程积分程序处理.
在例(1)中,时间和空间的区别很明显. 即使在没有明显区别的时候,本教程也将用"空间"和"时间"变量. "空间"变量是那些要离散化的变量. "时间"变量是在常微分方程组中所剩下的一个有待积分的变量.
|
|
| |
| TemporalVariable | Automatic | 哪个针对导出的常微分方程组或微分代数方程组,哪个变量将保留导数项. |
| Method | Automatic | 使用何种方法对常微分方程或微分代数方程进行积分 |
| SpatialDiscretization | TensorProductGrid | 使用何种方法进行空间离散 |
| DifferentiateBoundaryConditions | True | 是否对边界条件进行关于时间变量的微分 |
| ExpandFunctionSymbolically | False | 是否对有效函数进行符号式扩展 |
| DiscretizedMonitorVariables | False | 是否要把由 WhenEvent、诸如 StepMonitor 的监视器,或者如 Projection 等方法的方法选项给出的变量解释为空间变量的函数或者表示空间离散值向量 |

的选项.
部分选项的应用需要进一步了解直线方法的工作方式,这将在接下来的章节中解释.
当前,对空间离散所执行的唯一方法是

方法,它使用的是一个空间维度上的离散方法,并使用一个张量外积来推导矩形区域多个空间维度上的方法.

具有自己的选项集合,供您用来控制网格选择过程. 下面的各节提供了充分的背景信息,以便您能在必要时使用这些选项.
空间导数逼近
有限差分
中,有限差分与导数的区别在于导数值是

无限趋向于零时得到的极限值,而有限差分使用的是与相邻点

的有限间距,因此得到的是一个近似值.
推导得到,这种方式更为有用,因为它提供了一个误差估计(假设足够平滑)
该公式的重要一点是,

必须位于

和

之间,以使误差局限于包含采样点的区间内部. 对于有限差分公式,误差对与模板或样本点集具有局域性这一点在通常情况下是正确的. 对于收敛性或其它分析,误差通常表达为渐近形式:
这个公式通常被称为一阶向前差分. 向后差分使用的是

.
并求解

,可得到一阶导数的二阶中心差分公式
如果把刚才的泰勒公式再多扩展一阶并进行相加,然后结合刚才给出的公式,不难得到二阶导数的中心公式.
注意尽管两点之间为均匀步长

使得公式的便于推导,这并不是必需的. 比如,一般地,二阶导数的近似式为
其中

对应于最大的局部网格间距. 请注意三点公式的渐近阶已降至一阶;在均匀网格上是二阶的原因是来自偶然相消.
一般地,只要样本点的数量足够,渐进误差为任意阶的任何阶导数公式都可由泰勒公式推导得到. 然而,该方法如果用于比以上所示更为复杂的问题的求解,则会变得繁琐低效. 另外一种方法基于多项式插值:泰勒公式对于足够低阶的多项式来说是精确形式(无误差项),有限差分公式也是如此. 不难证明有限差分公式等价于插值多项式的导数. 例如,推导刚才所示的二阶导数公式的一个简单方法是进行一个二次式插值并找到它的二阶导数(其实就是逐项系数).
这里对三个点

,

和

进行多项式插值,并通过求导,得到了二阶导数的三点有限差分公式.
| Out[9]= |  |
通过公式的这种形式,容易看出它实际上是向前和向后一阶导数逼近之差. 有时,用这种方式使用有限差分是有时是有其优点的,尤其对于导数内部含有系数的项,如通常出现在偏微分方程中的

.
通过考虑插值公式,另外一个性质可以显而易见,那就是得到导数逼近值的点不一定要在网格上. 这个性质的一个常见用途是交错网格,这种情况下,想要的导数可能在网格点的中点处.
在一个均匀交错的网格

上,生成一个一阶导数的四阶逼近,其中主网格点

在

处,

为奇数.
| Out[10]= |  |
该式的四阶误差公式为

,而对于下面导出的标准四阶公式,则是

. 误差的减少大部分归结于模板尺寸的减小.
| Out[11]= | 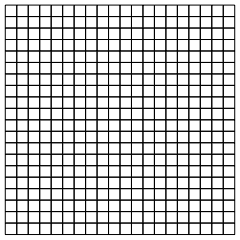 |
一般地,使用

个点的有限差分公式在函数为

次多项式,且渐进阶至少为

时是准确的. 在均匀网格上,可以期望得到更高的渐进阶数,尤其是对于中心差分而言.
使用高效的多项式插值法是生成系数的一个适当途径,但 B. Fornberg 开发了一种快速算法用于有限差分权重生成 [
F92], [
F98],这种方法明显要快得多.
在 [
F98] 中,Fornberg 展示了一种用于显式有限差分的一行
Mathematica 公式.
这是在一个均匀网格上生成权重的 Fornberg 的简单公式. 这里,该式稍微有所改变,将其变成一个函数定义.
这里,

是导数的阶,

包含在模板内的网格区间数,

是导数逼近所在的点与模板最左边的点之间的网格区间数.

不必是整数;非整数值仅会导致交错网格近似. 设置

为

总会生成一个中心公式.
| Out[13]= |  |
这个表格中要注意的一点是,公式与中心偏离越远,误差项系数越大,有时大几百倍. 有鉴于此,有时在需要单边的导数公式时(例如在边界处),将使用较高阶的公式来抵消额外的误差.
NDSolve`FiniteDifferenceDerivative
Fornberg [
F92],[
F98] 还给出了一个算法,尽管不是非常简单与优良,但更具有一般性,尤其适用于非均匀网格. 在
Mathematica 中对它编程并不困难,但为了尽可能使之高效,我们提供了一个新的内核函数作为一个更简单的接口(还有一些其它性能).
| NDSolve`FiniteDifferenceDerivative[Derivative[m],grid,values] |
| 求在网格上取值的函数的 m 阶导数的逼近 |
| NDSolve`FiniteDifferenceDerivative[Derivative[m1,m2,...,mn],{grid1,grid2,...,gridn},values] |
| 求含有 n 个变量的函数的 ( , ,  , ..., , ...,  ) 阶偏导数的近似,函数在张量积网格上取值,网格由 ( ) 阶偏导数的近似,函数在张量积网格上取值,网格由 ( , ,  , ..., , ...,  ) 的外积定义 ) 的外积定义 |
| NDSolve`FiniteDifferenceDerivative[Derivative[m1,m2,...,mn],{grid1,grid2,...,gridn}] |
| 计算所需的有限差分权重,以求含有 n 个变量的函数的 ( , ,  , ..., , ...,  ) 阶偏导数的近似,函数在张量积网格上取值,网格由 ( ) 阶偏导数的近似,函数在张量积网格上取值,网格由 ( , ,  , ..., , ...,  ) 的外积定义;结果以 ) 的外积定义;结果以  返回,它可以重复应用于网格上的值 返回,它可以重复应用于网格上的值 |
定义一个均匀网格,各点通过符号距离

分开.
| Out[14]= |  |
给出一个符号表示的函数

在网格上的一阶导数式.
| Out[15]= |  |
端点处的导数值通过单边公式计算. 前面一个例子中所示的公式精确到四阶,这是系统的默认设置. 一般地,如果使用符号网格和/或数据,得到的将是符号式. 这对于方法的分析非常有用;然而对于实际的数值网格,给

以数值网格而不使用符号式通常会更快、更准确.
定义一个

到

之间的随机间距网格.
| Out[16]= | 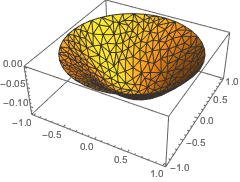 |
| Out[17]= |  |
| Out[18]= | 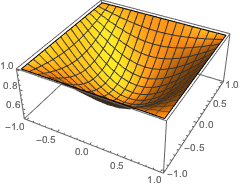 |
在多维情况下,

适用于张量积网格,您只需指定每个维度上的网格点.
定义在

和

方向上的网格

和

,得到高斯式在

和

的张量积上的混合型

偏导数的逼近,并绘制误差的曲面图.
| Out[23]= | 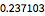 |

不计算导数和的权重. 这意味着对于一般的算符如拉普拉斯算符,您需要将两个逼近值组合.
使用该函数对在前面一个例子中所用的同一网格和高斯函数求拉普拉斯算符的逼近.
| Out[25]= | 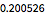 |
|
|
| |
| "DifferenceOrder" | 4 | 误差的渐进阶 |
| PeriodicInterpolation | False | 是否考虑为周期等于网格所包含的区间的周期函数的值 |
用于

的选项.
假设函数周期性重复,在前面定义的随机网格上求正弦函数的导数的逼近值.
| Out[26]= | 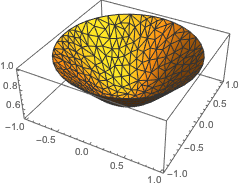 |
当使用
PeriodicInterpolation->True 时,可以忽略值中的最后一个点,因为它总是与第一个点相同. 这个特征在求解周期性边界条件的偏微分方程时很有用.
| Out[27]= |  |
四阶差分通常能够均衡机器精度的截断(逼近)误差和舍入误差. 然而,在一些场合下,四阶差分会产生过度振荡(Gibb 现象),因此二阶差分更为理想. 另外,在高精度时,高阶差分可能会更合适.

的偶数值使用中心公式,这时的误差系数通常比非中心公式时要小,因此若情况允许,推荐使用偶数值.
NDSolve`FiniteDifferenceDerivativeFunction
在计算一个偏微分方程的解时,通常需要将同一个有限差分逼近值重复应用于相同网格上的不同值. 通过存储必要的权重计算并将其应用于变化的数值,可以显著节省计算量. 如果在

中忽略带有函数值的(第三个)参数,结果将是一个

,这是一个以高效形式存储权重计算以便将来重复利用的数据对象.
| NDSolve`FiniteDifferenceDerivative[{m1,m2,...},{grid1,grid2,...}] |
| 计算对偏导数进行逼近所需的有限差分权重,函数是由 ( , ,  , ...)的外积定义的张量积网格上的 n 个变量的函数,偏导数的阶依次为 ( , ...)的外积定义的张量积网格上的 n 个变量的函数,偏导数的阶依次为 ( , ,  , ...) ;返回的结果是一个 , ...) ;返回的结果是一个 对象 对象 |
| NDSolve`FiniteDifferenceDerivativeFunction[Derivative[m],data] |
| 包含快速逼近函数的 m 阶导数所需的权重及其它数据的数据对象;在标准输出形式中,仅显示它所逼近的 Derivative[m] 算符 阶导数所需的权重及其它数据的数据对象;在标准输出形式中,仅显示它所逼近的 Derivative[m] 算符 |
| NDSolve`FiniteDifferenceDerivativeFunction[data][values] |
| 计算函数的导数逼近值,函数在用于确定数据的网格上取值 |
定义一个在单位区间上带有25个点的均匀网格,并计算网格上一个周期的正弦函数值.
| Out[4]= |  |
定义一个

,它可以重复应用于网格上的不同值以逼近二阶导数.
| Out[5]= |  |
注意标准输出形式被缩写了,仅显示被逼近的导数算符.
| Out[6]= |  |
该函数仅适用于在构建函数的特定网格上定义的值. 如果问题要求改变网格,您需要使用

来生成对应于每次网格变化的权重. 然而,如果您使用

对象,计算速度将显著加快.
比较用刚才定义的函数和用
前面一节的函数计算拉普拉斯算符所需的时间. 因为速度过快,不能通过
Timing 来显示时间的不同,因此在每个情形下都使用了一个循环来重复计算.
| Out[10]= |  |
一个

可重复用于多种情形. 作为一个简单的例子,请考虑一个在单位区间上求解边值问题
的配置法. (这个简单的方法并不一定是求解该特定问题的最佳途径,但作为示例而言却是非常有用的.)
定义一个函数,该函数的所有分量在边界值问题的逼近解处将为零. 使用中间向量

并将其端点设置为零(

部分)是一个快速且简单的强制实行边界条件的技巧. 除了数值

以外的所有计算被阻止,因为这在其它情况下不可行. (另外,由于
Times 的属性为
Listable,
Sin[2 Pi grid] u 将串起分量.)
使用
FindRoot 找到一个近似特征函数并显示其图形,该特征函数的初始值利用的是常系数情形.
| Out[14]= |  |
由于该问题设置得非常简单,很容易比较各种不同方案. 例如,要将上面的解(该解使用的是默认的四阶差分)与通常使用的二阶差分相比,只需要改变

.
这里使用二阶差分求解该边界值问题,并将它与四阶解的差异绘成图形显示出来.
| Out[41]= |  |
确定哪一个解更好的一种方式是研究随网格改善的收敛性. 这在"
微分矩阵"子节中进行了一定程度的讨论.
尽管

对象的最关键信息——导数的阶——在输出形式中得以显示, 将该信息及其它信息从

中提取有时是很有用的,例如在一个程序中使用. 数据存储方式的结构随
Mathematica 版本的不同可能有所变化,因此不推荐使用部分表达式来提取信息. 一种较好的替代方式是使用任何一种为此目的提供的方法函数.
令
FDDF 代表一个
NDSolve`FiniteDifferenceDerivativeFunction[data] 对象.
| FDDF@"DerivativeOrder" | 得到 FDDF 所逼近的导数阶 |
| FDDF@"DifferenceOrder" | 得到每个维度上进行逼近的带有差分阶数的列表 |
| FDDF@"PeriodicInterpolation" | 得到带有元素 True 或 False 的列表,指示周期性插值是否用于每个维度 |
| FDDF@"Coordinates" | 得到带有每个维度的网格坐标的列表 |
| FDDF@"Grid" | 形成网格点的张量;这是网格坐标的外积 |
| FDDF@"DifferentiationMatrix" | 计算稀疏微分矩阵 mat,使得 mat.Flatten[values] 等价于Flatten[FDDF[values]] |
从一个
NDSolve`FiniteDifferenceDerivativeFunction[data] 对象提取信息的方法函数.
任何一种方法函数,只要它返回的是带有每个维度的元素的列表,都可以结合一个整数参数
dim 使用,它将仅返回那个特定维度上的值,使得

.
这是一个

对象,由在每个维度上具有10到16个点的随机网格创建.
| Out[15]= |  |
| Out[20]= |  |
注意网格点张量的秩比张量积的维数多1. 这是由于定义每个点的三个坐标自身在一个列表中. 如果您有一个由网格变量决定的函数,您可以使用
Apply[f, fddf["Grid"], {n}],其中
n=Length[fddf["DerivativeOrder"]] 是您所要进行导数逼近的空间维数.
定义一个三变量高斯函数,并将其应用于定义

的网格上.
这里显示一个网格点的三维图形,网格点根据导数的按比例调整值进行上色.
| Out[23]= |  |
对于类如这个例子的中等大小的张量积网格,使用
Apply 还算快. 当网格尺寸变大时,这种方法可能不会是最快的,原因在于
Apply 与
Mathematica 编译器结合使用只有有限几种方式,因此与压缩数组结合使用的方式也有限. 如果您能够将函数定义为能够使用
Map 而不是
Apply,您可能能够使用
CompiledFunction,因为在
Mathematica 编译器内部,
Map 比
Apply 具有更广的应用性.
| Out[24]= |  |
如果可能的话,还有一种更好的方法,就是利用可列表性,这要求您的函数由具有
Listable 属性的函数和运算组成. 技巧是将

、

和

在张量积网格上各点处的值分离. 要做到这一点,最快的方式是使用
Transpose[fddf["Grid"]], RotateLeft[Range[n+1]]],其中
n=Length[fddf["DerivativeOrder"]] 是您所要逼近的导数所在的空间维数. 它将返回一个长度为
n 的列表,该列表对于每一个分量维度都具有网格上的值. 由于具有
Listable 属性,应用到该列表上的函数将遍布整个网格.
比较三种方法所用的时间. 指令被多次重复以得到更准确的计时.
| Out[26]= |  |
这些示例表明,使用
CompiledFunction 通常比使用
Apply 要快得多,利用列表属性(listability)也可以使速度有所加快.
拟谱导数
差分阶可取的最大值由网格点数决定. 如果超过极限,将给出一个提示信息,并且阶数自动降低.
使用最大阶数来逼近一个随机网格上正弦函数的一阶导数.

| Out[50]= |  |
使用一个极限阶数通常被称作拟谱导数. 一个常见问题是人为振荡(Runge 现象)会非常大. 然而有两种情形除外:具有周期重复性的均匀网格,和格点在切比雪夫多项式

零点或称 Chebyshev-Gauss-Lobatto 点的网格[
F96a], [
QV94]. 这两种情况均可以使用一种快速傅立叶变换进行计算,这种变换非常有效并且能够减小舍入误差.
| "DifferenceOrder"->n | 使用 n |
| "DifferenceOrder"->Length[grid] | 使用最高阶数有限差分在 grid 上逼近导数(一般不推荐使用) |
| "DifferenceOrder"->"Pseudospectral" | 使用拟谱导数逼近;仅适用于网格点间距与 Chebyshev-Gauss-Lobatto 点对应,或网格均匀且 PeriodicInterpolation->True |
| "DifferenceOrder"->{n1,n2,...} | 分别在维数 1, 2 ... 上使用差分阶  , , ... ... |
选项

的设置.
| Out[28]= |  |
计算每一个点处的误差. 逼近精确到舍入误差,因为一个周期函数在均匀网格上的拟谱导数的有效基是三角函数.
| Out[29]= |  |
Chebyshev-Gauss-Lobatto 点是

的零点. 利用性质

,可以看出它们在

处.
定义一个简单的函数,生成一个由

个点组成的网格,最左边的点在

处,区间长度

具有Chebyshev-Gauss-Lobatto 点的间距.
| Out[31]= |  |
| Out[32]= |  |
这里是导数的图形,使用一个相同点数的均匀网格在最大差分阶数下进行计算.
| Out[36]= |  |
尽管在中心处的逼近效果较好(因为在均匀网格上中心处点较密集),该图形还是很清楚地显示出阶数过高时有限差分逼近所常见的灾难性振荡. 利用 Chebyshev-Gauss-Lobatto 间距可以使这一问题最小化.
这幅图形显示的是利用周期性重复的均匀网格计算得到的拟谱导数逼近.
| Out[71]= |  |
周期性假设使逼近得以显著改善. 周期性拟谱逼近的准确性非常高,这使得在某些情况下有充分的理由来使用一个较大的域模拟计算周期,比如像这个例子一样的脉冲. 尽管这些逼近具有高度准确性,但并非没有缺陷:最严重的一种是重叠误差,即一个频率过高的振荡函数分量可能被错误逼近或完全消失.
有限差分逼近的精确性和收敛性
在使用有限差分时,重要的一点是要记住截断误差,即由截断泰勒级数逼近导致的渐近逼近误差,并不是误差的唯一来源. 在有限差分公式时误差还有两个其它来源;条件误差和舍入误差[
GMW81]. 舍入误差来自算术运算要求的四舍五入. 条件误差来自函数值任何误差的成倍放大,通常来自与步长的幂相除,因此随步长减小而增大. 这意味着,在实践中,即使截断误差随

趋近于零而趋近于零,实际误差将在超越某个点后开始增长. 下面的图形表示的是一个平滑函数在

变小时的典型行为.
这个对数图形表示的是,在机器精度下,高斯函数

在覆盖区间

的网格上各点处的一阶导数逼近的最大误差与网格点数的函数关系. 在均匀网格上阶数为2,4,6和8的有限差分分别用红、绿、蓝和紫红色表示. 均匀(周期性)间距及切比雪夫间距的拟谱导数分别用黑色和灰色表示.
这个对数图形表示的是,高斯函数

在覆盖区间

的网格上各点处的一阶导数逼近的截断误差(虚线)以及条件和舍入误差(实线)与网格点数

的函数关系. 在均匀网格上阶数为2,4,6和8的有限差分分别用红、绿、蓝和紫红色表示. 均匀(周期性)间距及切比雪夫间距的拟谱导数分别用黑色和灰色表示. 截断误差通过计算非常高精度的逼近得到. 舍入和条件误差的估计值通过高精度逼近值减去机器精度逼近值得到. 舍入和条件误差倾向于线性增长(由于一阶导数有限差分公式常见的

因子),对于较高阶导数往往也有所增大. 拟谱导数表现出更多的变化,这是因为FFT计算的误差随长度变化而变化. 注意均匀(周期性)拟谱导数的截断误差不会降低到

以下. 这是因为从数学角度而言,高斯函数并不是一个周期函数;这个误差在本质上给出了与周期性的偏离.
一个半对数图形,表示的是高斯函数

在覆盖区间

的45点网格上各点处的一阶导数逼近误差与

的函数关系. 在均匀网格上阶数为2,4,6和8的有限差分分别用红、绿、蓝和紫红色表示. 均匀(周期性)间距及切比雪夫间距的拟谱导数分别用黑色和灰色表示. 除了带有切比雪夫间距的拟谱导数外,其它全部利用均匀间距

计算. 很明显拟谱导数的误差并不是局域性的;这不足为奇,因为在任何点上的逼近都基于整个网格上的值. 有限差分的误差是局域性的,并且误差的大小随高斯函数的大小而变化(在半对数图形中是抛物线型).
从第二个图形可以明显看出,有一个得到最佳导数逼近的尺寸;对于较大的

,截断误差起主导作用,对于较小的

,条件和舍入误差起主导作用. 对于较高阶差分,优化的

往往能给出较好的逼近. 对于偏微分方程的空间离散化,这通常不是问题,因为精确度达到那个水平代价将会非常耗费资源. 然而,当使用较低阶的差分来逼近, 比如,雅克比矩阵时,这种误差均衡将是至关重要的. 为避免额外的函数计算,通常使用一阶向前差分,误差均衡与单位舍入的平方根成正比,所以挑选一个优良的

值非常重要 [
GMW81].
这些图形说明的是不存在真正的边界效应的平滑函数的典型情况. 如果改变高斯函数的参数,使函数变得更平,边界效应将开始出现.
一个半对数图形,表示的是高斯函数

在覆盖区间

的45点网格上各点处的一阶导数逼近误差与

的函数关系. 在均匀网格上阶数为2,4,6和8的有限差分分别用红、绿、蓝和紫红色表示. 均匀(非周期)间距及切比雪夫间距的拟谱导数分别用黑色和灰色表示. 除了带有切比雪夫间距的拟谱导数外,其它全部利用均匀间距

计算. 有限差分逼近的误差是局域性的,并且误差的大小随高斯函数一阶导数的大小变化而变化. 均匀间距拟谱(45阶多项式)逼近在边界附近的误差变得巨大;随着

减小,该误差是无界的. 另一方面,切比雪夫间距拟谱的误差更均匀,整体相当小.
到目前为止,所展示的例子似乎可以说明,逼近时阶数越要越好来越高的逼近阶越好. 然而,还有两个问题需要考虑. 逼近的阶数越高,函数计算越昂贵,如果需要隐式迭代(例如对于刚性问题),不仅计算雅克比式的代价高昂,矩阵的特征值也趋向于更大,从而导致更大的刚性,以及在迭代求解时的更大困难. 这是拟谱方法的一个极端,其中雅可比式基本上没有非零项 [
F96a]. 当然,这些问题对于较小的系统(以及矩阵)是一个折衷.
另一个问题与不连续性有关. 通常,多项式逼近的阶数越高,逼近的效果越差. 对于一个真正的不连续,更糟糕的是误差随网格间距减小而放大.
这个图形表示的是,不连续的单位阶跃函数
f(x)=UnitStep(x - 1/2) 在覆盖区间

的128点网格上各点处的一阶导数逼近与

的函数关系. 在均匀网格上阶数为2、4、6和8的有限差分分别用红、绿、蓝和紫红色表示. 均匀(周期性)间距及切比雪夫间距的拟谱导数分别用黑色和灰色表示. 除了带有切比雪夫间距的拟谱导数外,其它全部利用均匀间距

计算. 它们全部显示出振荡行为,但很明显,切比雪夫拟谱导数在这方面做得更好.
有众多替代方式可用于已知的不连续点周围,例如前端跟踪. 一阶向前差分能够减少振荡,但却引入了人为的粘性项. 一个较好的替代是所谓的实质不振荡方案(ENO),它偏离间断点用完全的阶,但在部连续点附近引入界限,限制了逼近阶数及振荡行为. 目前,ENO 方案不在
NDSolve 中执行.
总之,选择合适的差分阶数在很大程度上取决于问题的结构. 默认的4阶的选择一般是适合的,因为它适用于各种偏微分方程,但针对特定问题,您可能想尝试其它设置,以获得更好的效果.
微分矩阵
由于微分以及,自然地,有限差分逼近均是线性运算,表示

行为的一种替代方式是用矩阵. 表示微分算符近似的矩阵被称作微分矩阵 [
F96a]. 尽管微分矩阵并不总是应用有限差分逼近的最佳方式(尤其是当可以使用一个 FFT 来简化问题和减小误差时),它们对于辅助分析以及在线性求解程序中的应用是非常宝贵的,后者常常是求解偏微分方程时所需要的.
令
FDDF 代表一个
NDSolve`FiniteDifferenceDerivativeFunction[data] 对象.
| FDDF@"DifferentiationMatrix" | 将 FDDF 作为代表线性算子的矩阵,重新进行线性运算 |
这里创建了一个

对象.
| Out[37]= |  |
| Out[38]= |  |
矩阵是以稀疏形式给出,原因是微分矩阵一般具有相对较少的非零项.
Out[39]//MatrixForm=
|
|  |
这里说明,这三种表示方法就其对于数据的作用而言,基本上是等价的.
| Out[41]= |  |
正如前面所提到的,矩阵形式有利于分析. 例如,它可以用于直接求解程序,或者用于找寻特征值,从而可以在线性稳定性分析中使用.
| Out[42]= |  |
对于可通过快速傅立叶变换计算得到的拟谱导数,如果规模较小,使用微分矩阵可能较快,但在较大的网格上,FFT 由于其较好的复杂度及数值性能而成为更理想的选择.
对于多维导数,矩阵的形成使其在平面化的数据,即一维导数矩阵的
KroneckerProduct 上运算. 通过一个例子来理解这一点是最容易的.
计算网格上的一个高斯函数,该网格是在

和

方向上网格的外积.
定义一个

,利用四阶差分计算该函数的

-

混合偏导数.
| Out[7]= |  |
| Out[8]= |  |
注意该微分矩阵是一个1353×1353矩阵. 数字1353是在张量积网格上的总点数;当然也就是在

和

网格上的点数之积. 微分矩阵在一个数据向量上运算,该向量来自于张量积网格上的平面化数据. 该矩阵非常稀疏;非零项大概只有一个百分点的一半. 这在具有非零值的位置图中是显而易见的.
| Out[15]= |  |
对计算

-

混合偏导数的两种方法进行比较.
| Out[53]= |  |
| Out[17]= |  |
微分矩阵的使用会导致机器数值的略有不同,原因在于运算的顺序是不同的,进而导致了不同的舍入误差.
当想要得到的是导数的线性组合时,微分矩阵是非常有优势的. 例如,拉普拉斯算子的计算可以被放入单个矩阵中.
定义一个函数,在张量积网格上对拉普拉斯算子进行逼近.
| Out[18]= |  |
计算与在

和

方向上的导数相关的微分矩阵.
| Out[19]= |  |
将两个稀疏矩阵相加,得到拉普拉斯算子的一个单一矩阵.
| Out[68]= |  |
| Out[69]= |  |
比较对拉普拉斯算子进行逼近的这两种方法所得到的值和计算时间.
| Out[64]= |  |
离散化因变量的解释
当
WhenEvent 中给出的一个因变量在一个监视选项(如
StepMonitor)或在一个需要对该因变量进行解释的方法(如
Projection)中给出时,对于常微分方程,解释一般是清晰的:在时间(或该因变量)的某一个特定值,使用因变量所对应的那一部分解的值.
对于偏微分方程,解释却并不是这样明确. 从数学角度而言,在一个特定时刻的因变量是一个空间的函数. 这导致了默认的解释,它使用一个
InterpolatingFunction,作为空间区域上的逼近函数来代表因变量.
对于偏微分方程的另一种可能的解释是把在一个特定时刻的因变量看成是在那个时刻空间上离散化的值的表示——也就是说,既在时间也在空间上离散化. 您可以通过使用

选项
DiscretizedMonitorVariables->True 来要求监视程序和方法使用这种完全离散化的解释.
| Out[8]= |  |
在执行上述指令时,
StepMonitor 中的

实质上是关于

的函数,因此它可以用
Plot 来绘制. 也可以对它进行其它运算,例如数值积分.
| Out[11]= |  |
此时,

在每一步作为一个向量给出,向量由空间网格上的解的离散值组成. 在这个例子中,离散点的显示使之成为一个信息更丰富的监控,因为它使您可以看到前端在形成时的分辨情况.
值向量不含关于网格自身的信息;在这个例子中,图形是相对于指标值绘制,显示了一个均匀网格的正确间距. 注意当

被解释为一个函数时,网格将包含在用于表示空间解的
InterpolatingFunction 中,因此如果您需要网格,得到网格最简单的方法是从表示

的
InterpolatingFunction 中提取.
最后注意的是,使用离散化表示速度明显加快. 如果你正在使用诸如
Projection 或

的
WhenEvent 或者求解方法的表示时,这可能是很重要的. 使用事件检测防止解集超越计算区域的一个
例子,通过使用离散化解释使计算能更快进行.
边界条件
对于偏微分方程往往有可能决定一个良好的数值方法来对一个特定的方程和边界条件应用边界条件. 前面在
"直线数值方法"的引言中给出的例子就是如此. 然而,找到一个一般算法要困难得多,并且边界条件对刚度和整体稳定性的影响加剧了问题的复杂程度.
周期性边界条件特别易于处理:周期性插值用于有限差分. 由于均匀网格的拟谱逼近是准确的,通常可以很有效找到解.
| NDSolve[{eqn1,eqn2,...,u1[t,xmin]==u1[t,xmax],u2[t,xmin]==u2[t,xmax],...},{u1[t,x],u2[t,x],...},{t,tmin,tmax},{x,xmin,xmax}] |
| 求解函数  , , ... 的一个偏微分方程组,其中空间变量 x 具有周期性边界条件(假设 t 是一个时间变量) ... 的一个偏微分方程组,其中空间变量 x 具有周期性边界条件(假设 t 是一个时间变量) |
| NDSolve[{eqn1,eqn2,...,u1[t,x1min,x2,...]==u1[t,x1max x2,...],u2[t,x1min,x2,...]==u2[t,x1max x2,...],...},{u1[t,x1,x2,...],u2[t,x1,x2,...],...}, {t,tmin,tmax},{x,xmin,xmax}] |
| 求解函数  , , ... 的一个偏微分方程组,其中空间变量 ... 的一个偏微分方程组,其中空间变量  具有周期性边界条件(假设 t 是一个时间变量) 具有周期性边界条件(假设 t 是一个时间变量) |
如果您正在求解几个函数

,

...,如果任何函数具有周期性边界条件,则它们全部都必须有(仅需对一个函数指定条件). 如果空间维数大于1,则在某些自变量维度上具有周期性边界条件而其它没有是可行的.
这里利用拟谱法解出了一个广义Sine-Gordon 方程,该方程在两个空间维度上具有周期性边界条件. 如果不用周期性所允许的拟谱法,问题会要更长的时间来解决.
| Out[2]= |  |
在以解的形式返回的
InterpolatingFunction 对象中,

中的省略号用于表示这一维度的周期性重复.
这里将部分解绘制成一个曲面图,解从

处的周期性延续中推导得到.
| Out[3]= |  |
对于非周期性边界条件,
NDSolve 使用两种方法. 两者都有其优点和缺点. 第一种方法是相对于时间变量对边界条件进行微分,并对由此产生的微分方程(组)在边界处求解. 第二种方法是将每一个边界条件进行离散. 这通常会生成一个边界解的分量的代数方程,因此必须通过一个 DAE 求解程序求解. 这是通过

选项

控制的.
要了解微分法的工作原理,再次考虑直线法引言部分中的简单例子. 在第一个表达式中,在

处的 Dirichlet 边界条件是通过对

的微分来处置的. Neumann 边界条件利用反射思想来处置,该思想对于一个二阶有限差分逼近来说是可行的,但随阶数的升高,并不易于推广(尽管对于这个问题通过计算整个反射可以轻松完成). 但是,微分法却可以用于在

处Neumann 边界条件的任意阶的差分. 作为一个例子,该问题的一个解将使用四阶差分来得到.
这是对空间点数量和空间点之间间距的一种设置. 故意设置很小是为了使您可以看到结果方程式. 您可以以后进行更改,以提高逼近的准确性.

是边界条件的比例因子.
以下定义了

的向量.
| Out[5]= |  |
在

时,离散边界条件很简单,是

. 微分该方程并加入到条件中产生下式:
微分该方程并加上比例因子

乘以离散边界方程,可以得到一个新的方程.
| Out[7]= |  |
该方程的好处是通过包含导数,您将对该显式

求解,这样就可以把离散系统作为一组常微分方程来处理. 通过增加离散边界条件,该方程的解本身就渐进收敛于正确的边界条件,虽然有暂时的偏离或初始条件不一致. 这个可以从它的精确解中看到.
找到在

的导出边界方程的精确通解.
| Out[8]= |  |
比例因子的值将决定实际边界条件的解的收敛率. 该因子可以由
NDSolve 中选项
"DifferentiateBoundaryConditions"->{True, "ScaleFactor"->sf} 来控制.

的默认值是
Automatic,缩放因子

用于狄利克雷边界条件,在其他情况下,使用缩放因子

.
以下离散了在空间方向上

处的 Neumann 边界条件.
| Out[9]= |  |
以下求离散边界条件关于

的微分,并用来替代离散边界条件.
| Out[10]= |  |
从技术上讲,对边界条件进行离散不必使用与其余的微分方程相同的差分阶;事实上,因为单面导数的误差项要大得多,在边界处附近增加阶数往往是有必要的.
NDSolve 并没有这样做,因为差分阶数与
InterpolatingFunction 的插值阶数在空间方向上保持一致是可取的.
这是使用

来生成方程的另一种方法. 第一个和最后一个方程将被替换为源于边界条件的适当方程.
| Out[11]= |  |
| Out[14]= |  |
NDSolve 能够如同求解适当的导数一样求解该方程组,因此现在可以求解常微分方程.
| Out[16]= |  |
这幅图形显示的是边界条件在

处的满足程度.
| Out[16]= |  |
将边界条件当作代数条件处理,可以在使用 DAE求解程序为代价的前提下,节省好几步处理过程.
这里用对应于边界条件的代数条件替换(前面的)第一个和最后一个方程.
| Out[19]= |  |
| Out[20]= |  |
这里显示边界条件在

的的满足程度.
| Out[21]= |  |
对于这个例子,边界条件在两种情况下的容差范围内均得到很好的满足,但微分法做得稍好一点. 但并非总是如此;当边界条件被微分时,解可能会局部地漂离实际的边界条件.
绘制图形比较两种方法中狄利克雷边界条件在

处的满足程度. 由微分边界条件得到的解用黑色表示.
| Out[22]= |  |
当使用
NDSolve 时,通过选项

可以很方便地在两种方法之间切换. 应该记住的是,使用
DifferentiateBoundaryConditions->False 并不意味着您可以自由选择积分方法;所需方法必须是一个微分代数方程求解程序.
对于边界条件更加复杂的偏微分方程组或具有高阶导数的方程,可以调整两种方法使之适用于一般情况.当在一端有多个边界条件时,可能需要将某些条件附加到内部点上. 这个例子中的偏微分方程在空间区间的每一端都具有两个边界条件.
对在空间区间的每一端都具有两个边界条件的偏微分方程进行求解. 使用积分方法

是为了避免四阶导数稳定性的潜在问题.
| Out[23]= |  |
关于如何理解空间误差的提示信息将在下一节中介绍. 现在请暂时忽略该信息,只考虑边界条件.
| Out[21]= |  |
这里绘制一个对数图形,通过由
NDSolve 求解关于

的函数得到的解来说明这四个边界条件的满足程度.
| Out[25]= |  |
可以明显看出,边界条件在选项
AccuracyGoal 和
PrecisionGoal 允许的公差范围内得到了很好的满足. 通常,具有高阶导数的条件的满足程度要低于具有低阶导数的条件.
对于带有空间导数的边界条件,乘以原始边界条件的比例因子为零的原因有两个:首先,强加条件到离散方程只是一个空间近似,所以任何时候都让它尽可能精确没有意义;其次,尤其是高阶空间导数,当包括条件时,单边有限差分的大系数可能是潜在的不稳定源. 上面的例子在

的边界条件上就是这样的情况.

| Out[26]= |  |
以下的对数图,通过由
NDSolve 计算的作为

的函数的解,绘制了四个边界条件中每个条件的满足程度. 请注意最后一个的指数增长是一个不稳定的迹象.
| Out[28]= |  |
不一致的边界条件
有一点非常重要,即您所指定的边界条件既要与初始条件一致,也要与偏微分方程一致. 否则,
NDSolve 将发出一则警告信息来告知这种不一致性. 这种情况下,解可能不满足边界条件,更糟糕的是,可能会出现不稳定性.
在这个热方程例子中,在

处的边界条件明显与初始条件不一致.

| Out[2]= |  |
这里是在

处作为

的函数的解的图形. 边界条件

没有满足.
| Out[3]= |  |
边界条件没有满足的原因是因为常微分方程的积分起始于给定的初始条件. 在边界的微分方程一旦被微分,就变成

,因此解接近正确的边界条件,但在积分间隔中并不是很接近.
如果边界条件不被微分,微分代数方程求解程序实际上修改了初始条件使得边界条件得以满足.
DAE 求解器并不是总能找到产生像这样高效的正确解的一致初始条件. 改善用 ODE 方法求解的一个办法是使用
"DifferentiateBoundaryConditions"->{True, "ScaleFactor"->sf} 中高于默认值1的更高的边界条件比例因子值.
在这个热导方程中,在

的边界条件很明显与初始条件不一致.
以下绘制了作为

的函数的解在

处和边界条件

的值的不同. 很明显,随着比例因子的增加,在允许误差内,边界条件能更快地得到满足.
| Out[7]= |  |
| Out[8]= |  |
当比例因子很大时,求解器更难对方程进行积分,因为它引入一个可能的刚度源. 在比例因子为100的解中,就有一个变化很快的初始瞬间.
| Out[9]= |  |
处理这个问题的一个更保险的方法是给出一个与边界条件一致的初始条件,即使它不连续也行. 这种情况下,单位阶跃函数可以胜任此项任务.
这里使用一个不连续的初始条件来匹配边界条件,给出的解相对于空间离散化的分辨率而言是正确的.
| Out[13]= |  |
一般地,如果存在不连续的初始条件,空间误差估计是不能被满足的. 由于它们是根据平滑度估计的,因此一般情况下,最好是对您所希望模拟的不连续性效果进行选择,具体方法是,给出逼近不连续性的平滑函数,或者显式指定空间离散化所用的点的数目. 关于空间误差估计和离散化的更多细节在
"空间误差估计"中提供.
一种更微妙的不一致情况出现在当时间变量具有高阶导数且边界条件可能被多次微分时.
初始条件

满足边界条件,因此您可能会对
NDSolve 发出
NDSolve::ibcinc 信息很惊讶.
在这个例子中,边界和初始条件乍一看是一致的,但实际上在微分时会表现出不一致性.

| Out[8]= |  |
不一致性出现在您对第二个初始条件进行关于

的微分,给出

以及对第二个边界条件进行关于

的微分,给出

时. 两者在

时出现不一致.
偶然地,
NDSolve 会在边界条件实际上一致时发出不一致的提示信息
NDSolve::ibcinc. 这种情况来自于逼近 Neumann 边界条件或任何涉及到空间导数的边界条件时的离散化误差. 原因是,用于确定离散化点数的空间误差估计(见
"空间误差估计")基于偏微分方程和初始条件,而不是边界条件. 此外,用于近似边界条件的单边有限差分式比相同阶数的中心公式误差要大,从而导致边界处的附加的离散化误差. 这通常不是一个问题,但构造问题确实已经发生的例子是可能的.
在该例中,由于离散化误差,
NDSolve 错误地发出不一致边界条件的警告信息.

| Out[9]= |  |
边界条件图形表明,误差尽管不大,但却在默认的公差范围以外.
| Out[10]= |  |
当边界条件一致时,一种修正该错误的方法是指定
NDSolve 使用更精细的空间离散.
通过一种更精细的空间离散,提示信息不再出现,边界条件得以更好的满足.
| Out[14]= |  |
空间误差估计
概述
当
NDSolve 求解一个偏微分方程时,除非您已通过显式指定或给

和

选项相等的值来指定了空间网格,否则
NDSolve 需要进行空间误差估计.
理想情况下,空间误差估计会随着时间的推移得到监测,空间网格根据解的演变而更新. 网格自适应性的问题对于特定类型的偏微分方程是一个难题,当然也没有以任何一般性的方式解决. 此外,诸如局部细化等技术对于直线法存在一定问题,因为改变网格点的数量,需要完全重新启动常微分方程方法. 移动网格技术给这种办法带来了希望,但目前,
NDSolve 使用的是一个静态网格. 所用网格由一个基于初始条件的先验误差估计来确定. 在时间区间的结束,将进行一个事后检查来考察其一致性是否合理,如果检查没有通过,则发出警告信息. 这一点当然可以被愚弄,但实际上它提供了一个可接受的折衷. 失败的最常见的原因是当初始条件没有多大变化时,所以估计基本上是没有意义的. 在这种情况下,您可能需要自行选择适当的网格设置.
先验误差估计
当
NDSolve 利用直线法求解一个偏微分方程时,将需要就一个适当的空间网格上作出决定. 要完成这项任务,
NDSolve 利用的是一个基于初始条件(也就是先验条件)的误差估计.
最简单的是通过一个实例来说明其工作原理. 出于演示目的,可以考虑具有周期性边界条件的一维Sine-Gordon 方程.
这里对高斯初始条件下的 Sine-Gordon 方程求解.
| Out[59]= |  |
| Out[60]= |  |
时间点是由常微分方程方法基于局部误差控制而适应性做出选择的.
NDSolve 采用97(如果包括周期性端点则是98)个空间点. 这一选择将通过随后的步骤作一说明.
在
NDSolve 的方程处理阶段,首先发生的事件之一是具有二阶(或高阶)时间导数的方程被只有一阶时间导数的方程组所替代.
这是一个与前面的 Sine-Gordon 方程等价的一阶方程组.
| Out[61]= |  |
这是时间导数的解,方程右端是正则(常微分方程)形式.
| Out[62]= |  |
现在的问题是选择一个均匀网格来逼近导数,局部误差的容差由
AccuracyGoal 和
PrecisionGoal 指定. 对于这个例子,使用默认设置的

(4) 及默认设置的
AccuracyGoal 和
PrecisionGoal (对于偏微分方程均为4). 对离散得到的常微分方程组进行积分所用的方法,其自身的误差估计是建立在函数值足够精确的假设基础之上的. 此处估计的目的在于寻找一个空间网格,使得空间误差与局部时间误差(至少在初始条件下)能够保持平衡.
该误差估计基于 Richardson 外推法. 如果您知道误差是

,并且在

的两个不同值

和

处有两个逼近

和

,则事实上您可以外推至极限

从而得到一个误差估计
因此

的误差估计为
这里,

和

是长度不同的向量,而

是一个函数,因此您需要选择一个适当的范数. 如果选择

,那么您可以在两个向量公有的分量上简单地使用一个缩放后的范数,即所有的

和

的所有的间隔点. 这是一个很好的选择,因为它不需要任何网格之间的插值.
如果您想要在一个给定区间上设置一个均匀网格,您可以定义一个函数

,其中

为使得网格为

的区间长度,

.
为 Sine-Gordon 方程定义函数,返回步长

和一列网格点作为

的函数.
如果网格给定,可以利用有限差分对该方程进行离散化. 这可以通过

轻松实现.
这里定义 Sine-Gordon 方程右端的一个符号式离散化作为网格的函数. 它返回的是一个关于

和

的函数,以列表形式给出

和

的逼近值. (请注意,尽管下面仅使用了均匀网格,但原则上讲这对于任何网格均适用,不论其均匀与否.)
对于一个给定步长和网格,您也可以对

和

的初始条件进行离散.
这里定义一个函数,来将

和

的初始条件进行离散. 最后一个网格点被丢弃,这是因为由于周期性延续,它被认为与第一个网格点相同.
所感兴趣的量是在该初始条件下,

取一特定值时方程右端的逼近.
定义一个函数,在给定步长和网格的初始条件下,返回一个由方程右端逼近值组成的向量. 向量被展平以简化后继分析.
以

的一个特定值开始,通过生成

和

个点的右端,您可以获得误差估计.
| Out[72]= |  |
| Out[73]= |  |
如前所述,在

点网格上每隔一个点都在

点网格上. 因此,为简便起见,您可以使用一个范数,仅比较两个网格的公共点. 由于最终目标是满足绝对和相对公差标准,使用一个缩放的范数是合理的. 缩放时,除了考虑右边的大小,还必须包括网格上

和

相应组分量的大小,因为右边的误差最终包括在

和

中.
| Out[75]= |  |
根据 Richardson 外推公式 (3),要得到误差估计,只需将该值除以

.
这里计算

时的误差估计. 由于它基于一个缩放后的范数,如果结果小于1即满足公差标准.
| Out[76]= |  |
这里创建一个函数,将前面的函数组合在一起,以

的函数形式给出一个误差估计.
目标是要找到

的最小值,使得误差估计小于或等于1(因为它基于一个缩放后的范数). 原则上,将有可能使用求根算法,但由于

只能是整数,这将由过于复杂而且不得不调整停止条件. 一个较为简单的解决方案是使用 Richardson 外推公式来预测什么样的

值是恰当的,并重复预测过程,直到得到适当的

.
这里计算预测的最佳

值,依据的是先前计算的

时的误差估计.
| Out[78]= |  |
计算

取新值时的误差估计.
| Out[79]= |  |
通常情况下,以非常粗糙的网格为基础的预测将是不够的. 粗糙的网格可能会完全遗漏解的某些特征,这些特征可能会在一个更精细的网格上导致误差. 此外,由于误差估计基于渐近公式,因此对于粗糙间距,估计本身可能不是很好,即使所有解的特征在一定程度上得到分辨的情况下也是如此.
在实践中,计算这些误差估计可能相当耗费资源. 此外,没有必要非找到最优化的

,只要能够满足误差估计即可. 请记住,一切都可以随偏微分方程的演变而改变,因此根本不值得付出过多努力只为初始时间来寻找最佳间隔. 一个简单的解决办法是在新的

的预测公式中包括一个额外的大于1的因数. 即使有一个额外的因数,还是可能需要一些迭代来得到一个可接受的值. 但是,它通常使该进程加快.
定义一个函数,可给出网格点数目的预测值,它应满足误差估计.
| Out[81]= |  |
重要的是要注意,此过程必须有一个限制值,因为它可能无法满足误差的公差,例如在初始函数不连续时. 在
NDSolve 中,
MaxSteps 选项提供了这一限制;对于空间离散,这在所有空间维度上的默认值为10000.
拟谱导数不能使用该误差估计,原因是它们具有指数收敛而不是多项式收敛. 根据前面用到的公式,在极限
p->Infinity 时可以对误差作出一个估计. 这样做实际上是认为结果在更精细的网格上是准确的,并依据它们的差进行误差估计,因为

趋近于

. 一种更好的方法是利用这样一个事实:在一个给定的

点网格上,拟谱方法为

. 比较两个网格时,对于

使用较小的

是合理的. 就确定网格大小这一目的而言,这种做法提供了一种不完美但却充分的估计.
相似地,也可以对预测公式进行修改,启用

而不是

.
修改函数,使其能够用于拟谱导数,对

的适当值进行预测. 这种公式化并不试图挑选一个高效率的 FFT 长度.
在最终确定拟谱方法的

时,还要考虑的是,这个值不仅要满足公差条件,还要是计算 FFT 的一个高效率的长度. 在
Mathematica 中,高效率的 FFT 不需要二的幂的个长度,因为
Fourier 命令具有一个内置素因子算法.
通常,差分阶对满足误差估计所要求的点数有深远的影响.
创建一个表格,表示满足先验误差估计所要求的点数与差分阶的函数关系.
Out[84]//TableForm=
|
|  |
所要求的点数与差分阶的函数关系表格对解释为何直线法的默认设置是

大有帮助. 从2到4的改进通常是最显著的,并且在默认的公差范围内,四阶差分一般不会产生像在更高阶数时所可能出现的大的舍入误差. 拟谱差分往往是一个不错的选择,尤其在具有周期性边界条件时,但如果将它们作为默认设置并不好,原因是它们导致雅克比满矩阵,对于刚性方程生成和求解都可能会非常耗费资源.
对于非周期性网格,仅利用内部点即可完成误差估计. 原因是导数在边界附近处的误差系数是不同的. 这虽然可能会遗漏边界附近的特征,但主要思想是使估计保持简单易行,因为不管怎样,偏微分方程的发展可能会改变一切.
对于多个空间维度,则逐个维度逐次地作出决定. 由于在一个维度上的较好的分辨率可能会改变对另一个维度的要求,该过程逆序重复,以改善选择.
后验误差估计
通过
NDSolve 计算一个偏微分方程的解时,最后一步是对演化后的解进行一个空间误差估计,如果误差过大,将发出警告消息.
这些错误估计的方式与前面描述的先验估计类似. 唯一真正的区别是,估计错误所用的不是

和

点网格,而是

和

点网格. 这是因为,在

点网格上值的生成离不开差值法,而差值法自身会导致误差,但是在

点网格上的值是现成的,只需间隔取值即可. 这在 Richardson 外推公式中是很容易做的,利用

,得到
定义一个函数(基于前面一节所定义的函数),由以向量方式表示的

和

的解,计算关于 Sine-Gordon 方程的解的误差估. 由于该函数应用于一个已经构建好的网格上,因此已被定义为一个网格的函数. (注意,正如此处所定义的,这仅适用于偶数长度的网格. 处理奇数长度并不困难,但那样会使函数更加复杂.)
求解高斯初始条件下的 Sine-Gordon 方程.
| Out[98]= |  |
| Out[93]= |  |
创建一个函数,给出

取某一特定数值的后验误差估计.
绘制后验误差估计与

的函数关系图形.
| Out[99]= |  |
在这个函数中所看到的大量局部差异是典型的. (在本例中,这个大的峰值正好出现在原来的单峰分裂成分立的波的时候.)由于这个原因,除非这一估计超过10(而不是1,1用来选择基于初始条件的网格),
NDSolve 不会对过度的误差发出警告. 后验误差估计不如先验误差估计准确这一事实进一步证明了额外因子10的合理性. 因此,当
NDSolve 基于后验误差估计发出警告信息时,通常是因为解的新的特征已经出现,或者因为在求解过程中的不稳定性.
这个例子使用的是与前面的例子相同的初始条件,但
NDSolve 基于后验误差估计给出一个警告信息.

| Out[46]= |  |
这里显示的是解在

时的图形. 很明显,警告信息是适当的,因为临近峰值处的振荡是非物理的.
| Out[47]= |  |
如果不出现
NDSolve::eerr 信息,则可能有必要通过使用选项来控制网格选择过程,原因是默认设置有可能并没有找到一个准确解.
控制空间网格选择
直线法的
NDSolve 实现有几种方式来控制空间网格的选择.
所有用于张量积网格离散化的选项可以用一个列表给出,列表长度等于空间维数,在这种情况下,各个空间维度的参数由列表中相应的组成部分确定.
除了非周期性问题的拟谱方法外,离散通过均匀网格实现,所以当在一个区间长度

上求解问题时,在

和

选项之间有一个直接对应.
选项

被有效地转化为等价的

值. 这样只是为了提供方便,因为有时问题的设定与步长能更自然的联系在一起,而不是与离散点的个数. 当给

和对应的

选项指定除了
Automatic 以外的值时,使用的限制条件一般更严格.
在
前面一节所示的一个例子中,由于解的图线逐渐变陡,解的分辨并不充分. 接下来的示例将展示一些修改网格参数的不同方法,以便接近激波的解能更好地分辨.
一种避免这种解随图线变陡而出现的振荡的方法是要确保在图线最陡在的地方使用的点数足够多来分辨解解. Burgers 方程
的单峰解中,可以证明 [
W76],在

时,激波宽度与

成正比. 超过95%的变化包含在一个宽度为

的层内. 因此,如果您选择一半激波宽度的最大步长,总是会有一点在激波的陡峭部分,因而有希望在没有显著振荡的条件下对其进行分辨.
此处计算 Burgers 方程的解,使得有足够多的点求来分辨激波.

| Out[49]= |  |
注意单单分辨波形绝不足以满足
NDSolve 的默认公差,这需要一个

的精确度. 然而,一旦您有足够的点来分辨基本图线,根据
NDSolve::eerr 提示信息中所示的后验误差估计进行预测并非不妥(可再增加10%,因为,说到底它只是一个预测).
这里计算 Burgers 方程的解,最大步长的选择足够小,以满足基于由先前计算的误差所得预测的默认公差.
| Out[51]= |  |
要比较这样的解,有必要来观察一个只包含空间网格点处解的图形. 由于网格点作为
InterpolatingFunction 的一部分存储,定义一个实现这种功能的函数相当简单.
定义一个函数,仅绘制

时刻在空间网格上的点.
绘制一个图形,比较在

处得到的三个解.
| Out[53]= |  |
在这个例子中,区域的左端实在不需要这么多点. 点需要在图线陡峭的地方群集,因此显式指定一个网格使之在这种地方有较多的点,或许是一种明智的考虑.
在一个预先指定的网格上求解 Burgers 方程,网格的大部分点聚集在

的右边.
| Out[56]= |  |
| Out[57]= |  |
许多同样的原则适用于多个空间维度. 在两个维度上各向异性的 Burgers 方程提供了一个很好的例子.
这里求解一个在

和

方向上具有不同速度的二维 Burgers 方程的变体.

| Out[59]= |  |
这是解在

处的前缘曲面图.
| Out[60]= |  |
与一维情形相似,前缘变得陡峭. 由于速度项 (

) 较大,陡峭显得并不怎么极端,这个默认的解实际上对前端分辨得相当不错. 因此,应该可以从误差估计来预测,以满足默认公差. 一个简单的缩放参数表明,图线宽度在

方向上会比在

方向上窄

倍. 因此,

方向的步长比

方向的步长大这样一个因数是有道理的,或者最小点数可以相应地小上

个因数.
这里求解 Burgers 方程的二维变体. 该方程在

和

方向具有由前面计算中的后验误差估计预测的适当步长限制,前面的计算中在

方向上是69个点.
| Out[62]= |  |
这个解用了大量的时间来计算,这并不奇怪,因为该过程涉及到对超过18000个常微分方程组成的系统求解. 在许多情况下,特别是在一个以上的空间维度上,满足默认公差可能是不切实际的,所以你可能需要适当使用
AccuracyGoal 和/或
PrecisionGoal 来降低公差要求. 有时,特别是当网格由于不太严格的公差而较粗糙时,该系统不是刚性的,有可能使用显式方法避免数值线性代数. 数值线性代数可能会有问题,尤其在处理高维问题时. 在这个例子中,使用方法
Method->ExplicitRungeKutta 得到解仅用了大约一半的时间.
网格的其他任何选项都可以以列表形式指定,来给出每个维度上的值. 当只给出一个单值时,该值将用于所有的空间维度. 有两种情况除外,一个是

,取单值作为外积网格的总点数,另一个是

,它的网格必须在每个维度上显式指定.
这里选择前面解的部分网格,在前端较陡峭的部分网格更密集.
| Out[65]= |  |
记住这样一点很重要,即空间的后验误差估计只是在计算空间导数时对局部误差的估计,可能无法反映一个给定解实际的空间累积误差. 获得实际空间误差估计的一种方法是计算在非常严格的时间容差下不同空间网格上的解. 为了说明这一工作原理,重新考虑较简单的一维 Burgers 方程.
这里计算一个解的列表,利用

的空间网格点,计算 Burgers 方程在差分阶数为2、4、6和拟谱时的解. 时间准确性和精度公差设定得非常高,所以基本上全部误差均来自空间离散化. 请注意,通过在
NDSolve 中指定

,只有在

的解被保存. 如果没有这种预防措施,更精细的网格(这需要更多的时间步)上的某些解可能用尽可用内存. 即便如此,解的列表还是需要的大量时间来计算.
鉴于存在两个解,需要在两者之间进行比较. 为了去除解自身以外的所有误差来源,最好是使用创建
InterpolatingFunction 所用的插值数据. 这可以通过使用两个解的公共点来完成.
定义一个函数,通过在公共点上比较这两个不同的解来估计误差. 参数

和

应分别是在粗糙和精细网格上的解. 这适用于先前网格间距以2的幂变化时所生成的解.
为了得到一个误差的一般趋势的指标(在不稳定的情况下,解不收敛,所以这种情况不予考虑),您可以比较相连的一对解的差异.
这里定义一个函数,将对给定差分阶数时得到的连续的解的误差估计序列绘制图形,并用它作出估计误差作为网格点数量的函数的对数坐标图.
| Out[71]= |  |
这里是一个 Burgers 方程在

处的逼近解的最大空间误差作为网格点数函数的对数坐标图. 在均匀的网格上阶数为2、4和6的有限差分分别显示为红色、绿色和蓝色. 均匀(周期性)间距的拟谱倒数显示为黑色.
在图形左上角部分是图线没有充分分辨的网格,所以差别只是数量级1(如果有不稳定性,情况将更加糟糕). 然而,一旦有足够数量的点来分辨没有振荡的波形,收敛将变得很迅速. 对数直线的斜率为

毫不奇怪,它对应于
NDSolve 默认使用的差分阶数. 如果网格足够精细从而进入渐近收敛的部分,可能像在前面两节中那样通过使用 Richardson 外推法进行一个简单的误差估计,但这是在整体解上,而不是局部误差. 另一方面,计算更多的值并观察图形能够指示您是否在渐近部分.
从图形中显见的是,最好的解是2049个点的拟谱解(具有更多点数的解没有计算,因为它的空间准确度远远超过了规定的时间公差). 这种解实际上几乎可视为一个确切的解,至少大致在

的公差以内如此.
要判断如何最佳的解决这个问题,有必要进行以下操作:对于得到的每个解,如果至少是一个合理的逼近,则重新对其计算,其中时间准确性公差的设定要与解可能的空间准确性相当,并将得到的准确度作为求解时间的函数绘制图形. 以下(有点复杂)的命令可实现这一目的.
这确定了将被使用的"最佳"解,它实际作为后面计算的精确解. 它被从要与它进行比较的解列表中去除,因为它自身的比较是没有意义的.
定义一个函数,在给定一个差分阶

和一个用该差分阶计算得到的解

的前提下,重新计算该解,其中局部时间公差比所得到的实际空间准确度稍微严格一些,如果该准确度已足够的话. 该函数输出是这样一个列表{网格点数,差分阶,计算所用秒数,重新计算所得解的实际误差}.
将该函数应用于先前计算的每一个解. (差分阶数要适当!)
| Out[75]= |  |
将没有重新计算的情形去除,并绘制准确度与计算时间的函数关系对数图.
| Out[76]= |  |
一个表示 Burgers 方程在

处的逼近解误差与计算时间的函数关系的对数图. 显示的每个点标明了用于计算解所用的空间网格点的数量. 在均匀网格上阶数为2、4和6的有限差分分别显示为红色,蓝色和绿色. 具有均匀(周期性)间距的拟谱导数用黑色显示. 注意拟谱方法的成本从513到1025大幅跳跃. 这是因为该方法已切换到刚性求解算法,该算法因离散化产生的密集雅可比矩阵而变得非常昂贵.
所得到的图形非常有力地表明,如果适用(比如这种情形),周期性拟谱逼近具有惊人的效率. 否则,在一定程度上,差分阶越高,一般逼近效果越好. 这些都是平滑问题的特征,该 Burgers 方程就是这样一个特例. 但一般在趋向极限

时,高阶解相当差.
最后要注意的一点是,上图在时间方向上的计算使用的是
Automatic 方法. 这用到了 LSODA,它根据解的演变方式在刚性和非刚性方法之间切换. 对于粗网格,严格显式的方法通常稍快,并且除了拟谱情况,隐式 BDF 的方法对于较精细的网格较快. 在
NDSolve 中有多种常微分方程的替代方法可用.
边界处的误差
该先验误差估计是在计算区域内部计算的,原因是在这里所用的差分都具有相容的误差项,可以用来有效地估计要用的点数. 将边界包括在误差估计内将使进程变得更为复杂,超出了这种先验估计所能保证的合理性. 通常情况下,这种方法能成功地将误差合理控制. 然而,有一些情况下可导致困难.
有时可能会因为边界处所用单边导数的误差项较大,
NDSolve 将检测到边界条件和初始条件之间的一种不一致性,这是离散误差的假缺陷.
这里求解左端恒温、右端向自由空间辐射的一维热传导方程.

| Out[2]= |  |
在这种情况下,
NDSolve::ibcinc 提示信息的发出完全是因为在右边界的较大离散误差. 对于这个特定的例子,额外的误差并不是一个问题,因为它由于方程的性质而逐渐减弱并消失. 然而,通过多用几个空间点就可以使这则消息消除.
计算与上面相同的方程的解,不同的是在

方向上使用了至少50个点.
| Out[3]= |  |
边界处的误差问题会意外影响到离散的另一种情形发生在周期性边界条件由一个并不具有真正周期性的函数给出时,这样一个无意识的不连续被引入到计算中.

| Out[5]= |  |
这里的问题是,当考虑周期性计算时,初始条件实际上是不连续的.
| Out[6]= |  |
由于在尖点处总是有一个大的导数误差,
NDSolve 被迫使用最大点数,试图满足先验误差界限. 更糟糕的是,极端的变化使求解由此产生的常微分方程更加困难,导致求解时间很长,使用大量的内存.
如果不连续性是确实想要的,您通常要指定空间网格中一定数目的点或间距,使之足以处理您所感兴趣的不连续性的各个方面. 模拟高精度的不连续性通常需要专门的方法,这超出了
NDSolve 所提供的一般方法的范围.
另一方面,如果不连续性是不想要的,例如这个例子中不连续只是由于选择的计算域过小而无意造成,这时问题通常可以通过延长区域或增加项使周期之间平滑过渡而轻松解决.
求解 Sine-Gordon 问题,计算域足够大以至初始条件中的不连续性与默认公差所允许的误差相比是可以忽略不计的.
| Out[8]= |  |
 处的 Neumann 边界条件稍微有点复杂. 关于二阶差分,一个处置这种问题的方法是通过反射:设想在区间
处的 Neumann 边界条件稍微有点复杂. 关于二阶差分,一个处置这种问题的方法是通过反射:设想在区间  上使用在
上使用在  和
和  处相同的边界条件对问题求解. 由于初始条件和边界条件关于
处相同的边界条件对问题求解. 由于初始条件和边界条件关于  对称,解应该始终关于
对称,解应该始终关于  对称,因此对称性质与在
对称,因此对称性质与在  处的 Neumann 边界条件等价. 因此
处的 Neumann 边界条件等价. 因此  ,
, .
.
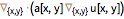
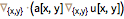
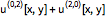
 方法,它使用的是一个空间维度上的离散方法,并使用一个张量外积来推导矩形区域多个空间维度上的方法.
方法,它使用的是一个空间维度上的离散方法,并使用一个张量外积来推导矩形区域多个空间维度上的方法.  具有自己的选项集合,供您用来控制网格选择过程. 下面的各节提供了充分的背景信息,以便您能在必要时使用这些选项.
具有自己的选项集合,供您用来控制网格选择过程. 下面的各节提供了充分的背景信息,以便您能在必要时使用这些选项. 必须位于
必须位于  和
和  之间,以使误差局限于包含采样点的区间内部. 对于有限差分公式,误差对与模板或样本点集具有局域性这一点在通常情况下是正确的. 对于收敛性或其它分析,误差通常表达为渐近形式:
之间,以使误差局限于包含采样点的区间内部. 对于有限差分公式,误差对与模板或样本点集具有局域性这一点在通常情况下是正确的. 对于收敛性或其它分析,误差通常表达为渐近形式:

 以数值网格而不使用符号式通常会更快、更准确.
以数值网格而不使用符号式通常会更快、更准确.
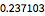
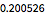

 的偶数值使用中心公式,这时的误差系数通常比非中心公式时要小,因此若情况允许,推荐使用偶数值.
的偶数值使用中心公式,这时的误差系数通常比非中心公式时要小,因此若情况允许,推荐使用偶数值. 中忽略带有函数值的(第三个)参数,结果将是一个
中忽略带有函数值的(第三个)参数,结果将是一个  ,这是一个以高效形式存储权重计算以便将来重复利用的数据对象.
,这是一个以高效形式存储权重计算以便将来重复利用的数据对象.

 并将其端点设置为零(
并将其端点设置为零( 部分)是一个快速且简单的强制实行边界条件的技巧. 除了数值
部分)是一个快速且简单的强制实行边界条件的技巧. 除了数值  以外的所有计算被阻止,因为这在其它情况下不可行. (另外,由于 Times 的属性为 Listable,Sin[2 Pi grid] u 将串起分量.)
以外的所有计算被阻止,因为这在其它情况下不可行. (另外,由于 Times 的属性为 Listable,Sin[2 Pi grid] u 将串起分量.)

 对象的最关键信息——导数的阶——在输出形式中得以显示, 将该信息及其它信息从
对象的最关键信息——导数的阶——在输出形式中得以显示, 将该信息及其它信息从  中提取有时是很有用的,例如在一个程序中使用. 数据存储方式的结构随 Mathematica 版本的不同可能有所变化,因此不推荐使用部分表达式来提取信息. 一种较好的替代方式是使用任何一种为此目的提供的方法函数.
中提取有时是很有用的,例如在一个程序中使用. 数据存储方式的结构随 Mathematica 版本的不同可能有所变化,因此不推荐使用部分表达式来提取信息. 一种较好的替代方式是使用任何一种为此目的提供的方法函数. 
 ,则不必构建 CompiledFunction,因为如果网格是一个压缩数组则编译将自动进行.)
,则不必构建 CompiledFunction,因为如果网格是一个压缩数组则编译将自动进行.) 、
、 和
和  在张量积网格上各点处的值分离. 要做到这一点,最快的方式是使用Transpose[fddf["Grid"]], RotateLeft[Range[n+1]]],其中 n=Length[fddf["DerivativeOrder"]] 是您所要逼近的导数所在的空间维数. 它将返回一个长度为 n 的列表,该列表对于每一个分量维度都具有网格上的值. 由于具有 Listable 属性,应用到该列表上的函数将遍布整个网格.
在张量积网格上各点处的值分离. 要做到这一点,最快的方式是使用Transpose[fddf["Grid"]], RotateLeft[Range[n+1]]],其中 n=Length[fddf["DerivativeOrder"]] 是您所要逼近的导数所在的空间维数. 它将返回一个长度为 n 的列表,该列表对于每一个分量维度都具有网格上的值. 由于具有 Listable 属性,应用到该列表上的函数将遍布整个网格. 零点或称 Chebyshev-Gauss-Lobatto 点的网格[F96a], [QV94]. 这两种情况均可以使用一种快速傅立叶变换进行计算,这种变换非常有效并且能够减小舍入误差.
零点或称 Chebyshev-Gauss-Lobatto 点的网格[F96a], [QV94]. 这两种情况均可以使用一种快速傅立叶变换进行计算,这种变换非常有效并且能够减小舍入误差.




 趋近于零而趋近于零,实际误差将在超越某个点后开始增长. 下面的图形表示的是一个平滑函数在
趋近于零而趋近于零,实际误差将在超越某个点后开始增长. 下面的图形表示的是一个平滑函数在  变小时的典型行为.
变小时的典型行为. 在覆盖区间
在覆盖区间  的网格上各点处的一阶导数逼近的最大误差与网格点数的函数关系. 在均匀网格上阶数为2,4,6和8的有限差分分别用红、绿、蓝和紫红色表示. 均匀(周期性)间距及切比雪夫间距的拟谱导数分别用黑色和灰色表示.
的网格上各点处的一阶导数逼近的最大误差与网格点数的函数关系. 在均匀网格上阶数为2,4,6和8的有限差分分别用红、绿、蓝和紫红色表示. 均匀(周期性)间距及切比雪夫间距的拟谱导数分别用黑色和灰色表示.  在覆盖区间
在覆盖区间  的网格上各点处的一阶导数逼近的截断误差(虚线)以及条件和舍入误差(实线)与网格点数
的网格上各点处的一阶导数逼近的截断误差(虚线)以及条件和舍入误差(实线)与网格点数  的函数关系. 在均匀网格上阶数为2,4,6和8的有限差分分别用红、绿、蓝和紫红色表示. 均匀(周期性)间距及切比雪夫间距的拟谱导数分别用黑色和灰色表示. 截断误差通过计算非常高精度的逼近得到. 舍入和条件误差的估计值通过高精度逼近值减去机器精度逼近值得到. 舍入和条件误差倾向于线性增长(由于一阶导数有限差分公式常见的
的函数关系. 在均匀网格上阶数为2,4,6和8的有限差分分别用红、绿、蓝和紫红色表示. 均匀(周期性)间距及切比雪夫间距的拟谱导数分别用黑色和灰色表示. 截断误差通过计算非常高精度的逼近得到. 舍入和条件误差的估计值通过高精度逼近值减去机器精度逼近值得到. 舍入和条件误差倾向于线性增长(由于一阶导数有限差分公式常见的  因子),对于较高阶导数往往也有所增大. 拟谱导数表现出更多的变化,这是因为FFT计算的误差随长度变化而变化. 注意均匀(周期性)拟谱导数的截断误差不会降低到
因子),对于较高阶导数往往也有所增大. 拟谱导数表现出更多的变化,这是因为FFT计算的误差随长度变化而变化. 注意均匀(周期性)拟谱导数的截断误差不会降低到  以下. 这是因为从数学角度而言,高斯函数并不是一个周期函数;这个误差在本质上给出了与周期性的偏离.
以下. 这是因为从数学角度而言,高斯函数并不是一个周期函数;这个误差在本质上给出了与周期性的偏离. 在覆盖区间
在覆盖区间  的45点网格上各点处的一阶导数逼近误差与
的45点网格上各点处的一阶导数逼近误差与  的函数关系. 在均匀网格上阶数为2,4,6和8的有限差分分别用红、绿、蓝和紫红色表示. 均匀(周期性)间距及切比雪夫间距的拟谱导数分别用黑色和灰色表示. 除了带有切比雪夫间距的拟谱导数外,其它全部利用均匀间距
的函数关系. 在均匀网格上阶数为2,4,6和8的有限差分分别用红、绿、蓝和紫红色表示. 均匀(周期性)间距及切比雪夫间距的拟谱导数分别用黑色和灰色表示. 除了带有切比雪夫间距的拟谱导数外,其它全部利用均匀间距  计算. 很明显拟谱导数的误差并不是局域性的;这不足为奇,因为在任何点上的逼近都基于整个网格上的值. 有限差分的误差是局域性的,并且误差的大小随高斯函数的大小而变化(在半对数图形中是抛物线型).
计算. 很明显拟谱导数的误差并不是局域性的;这不足为奇,因为在任何点上的逼近都基于整个网格上的值. 有限差分的误差是局域性的,并且误差的大小随高斯函数的大小而变化(在半对数图形中是抛物线型). ,截断误差起主导作用,对于较小的
,截断误差起主导作用,对于较小的  ,条件和舍入误差起主导作用. 对于较高阶差分,优化的
,条件和舍入误差起主导作用. 对于较高阶差分,优化的  往往能给出较好的逼近. 对于偏微分方程的空间离散化,这通常不是问题,因为精确度达到那个水平代价将会非常耗费资源. 然而,当使用较低阶的差分来逼近, 比如,雅克比矩阵时,这种误差均衡将是至关重要的. 为避免额外的函数计算,通常使用一阶向前差分,误差均衡与单位舍入的平方根成正比,所以挑选一个优良的
往往能给出较好的逼近. 对于偏微分方程的空间离散化,这通常不是问题,因为精确度达到那个水平代价将会非常耗费资源. 然而,当使用较低阶的差分来逼近, 比如,雅克比矩阵时,这种误差均衡将是至关重要的. 为避免额外的函数计算,通常使用一阶向前差分,误差均衡与单位舍入的平方根成正比,所以挑选一个优良的  值非常重要 [GMW81].
值非常重要 [GMW81].  在覆盖区间
在覆盖区间  的45点网格上各点处的一阶导数逼近误差与
的45点网格上各点处的一阶导数逼近误差与  的函数关系. 在均匀网格上阶数为2,4,6和8的有限差分分别用红、绿、蓝和紫红色表示. 均匀(非周期)间距及切比雪夫间距的拟谱导数分别用黑色和灰色表示. 除了带有切比雪夫间距的拟谱导数外,其它全部利用均匀间距
的函数关系. 在均匀网格上阶数为2,4,6和8的有限差分分别用红、绿、蓝和紫红色表示. 均匀(非周期)间距及切比雪夫间距的拟谱导数分别用黑色和灰色表示. 除了带有切比雪夫间距的拟谱导数外,其它全部利用均匀间距  计算. 有限差分逼近的误差是局域性的,并且误差的大小随高斯函数一阶导数的大小变化而变化. 均匀间距拟谱(45阶多项式)逼近在边界附近的误差变得巨大;随着
计算. 有限差分逼近的误差是局域性的,并且误差的大小随高斯函数一阶导数的大小变化而变化. 均匀间距拟谱(45阶多项式)逼近在边界附近的误差变得巨大;随着  减小,该误差是无界的. 另一方面,切比雪夫间距拟谱的误差更均匀,整体相当小.
减小,该误差是无界的. 另一方面,切比雪夫间距拟谱的误差更均匀,整体相当小. 的128点网格上各点处的一阶导数逼近与
的128点网格上各点处的一阶导数逼近与  的函数关系. 在均匀网格上阶数为2、4、6和8的有限差分分别用红、绿、蓝和紫红色表示. 均匀(周期性)间距及切比雪夫间距的拟谱导数分别用黑色和灰色表示. 除了带有切比雪夫间距的拟谱导数外,其它全部利用均匀间距
的函数关系. 在均匀网格上阶数为2、4、6和8的有限差分分别用红、绿、蓝和紫红色表示. 均匀(周期性)间距及切比雪夫间距的拟谱导数分别用黑色和灰色表示. 除了带有切比雪夫间距的拟谱导数外,其它全部利用均匀间距  计算. 它们全部显示出振荡行为,但很明显,切比雪夫拟谱导数在这方面做得更好.
计算. 它们全部显示出振荡行为,但很明显,切比雪夫拟谱导数在这方面做得更好. 行为的一种替代方式是用矩阵. 表示微分算符近似的矩阵被称作微分矩阵 [F96a]. 尽管微分矩阵并不总是应用有限差分逼近的最佳方式(尤其是当可以使用一个 FFT 来简化问题和减小误差时),它们对于辅助分析以及在线性求解程序中的应用是非常宝贵的,后者常常是求解偏微分方程时所需要的.
行为的一种替代方式是用矩阵. 表示微分算符近似的矩阵被称作微分矩阵 [F96a]. 尽管微分矩阵并不总是应用有限差分逼近的最佳方式(尤其是当可以使用一个 FFT 来简化问题和减小误差时),它们对于辅助分析以及在线性求解程序中的应用是非常宝贵的,后者常常是求解偏微分方程时所需要的. 


 和
和  网格上的点数之积. 微分矩阵在一个数据向量上运算,该向量来自于张量积网格上的平面化数据. 该矩阵非常稀疏;非零项大概只有一个百分点的一半. 这在具有非零值的位置图中是显而易见的.
网格上的点数之积. 微分矩阵在一个数据向量上运算,该向量来自于张量积网格上的平面化数据. 该矩阵非常稀疏;非零项大概只有一个百分点的一半. 这在具有非零值的位置图中是显而易见的.

 选项DiscretizedMonitorVariables->True 来要求监视程序和方法使用这种完全离散化的解释.
选项DiscretizedMonitorVariables->True 来要求监视程序和方法使用这种完全离散化的解释.

 被解释为一个函数时,网格将包含在用于表示空间解的InterpolatingFunction 中,因此如果您需要网格,得到网格最简单的方法是从表示
被解释为一个函数时,网格将包含在用于表示空间解的InterpolatingFunction 中,因此如果您需要网格,得到网格最简单的方法是从表示  的 InterpolatingFunction 中提取.
的 InterpolatingFunction 中提取.  的 WhenEvent 或者求解方法的表示时,这可能是很重要的. 使用事件检测防止解集超越计算区域的一个例子,通过使用离散化解释使计算能更快进行.
的 WhenEvent 或者求解方法的表示时,这可能是很重要的. 使用事件检测防止解集超越计算区域的一个例子,通过使用离散化解释使计算能更快进行.
 选项
选项  控制的.
控制的. 处的 Dirichlet 边界条件是通过对
处的 Dirichlet 边界条件是通过对  的微分来处置的. Neumann 边界条件利用反射思想来处置,该思想对于一个二阶有限差分逼近来说是可行的,但随阶数的升高,并不易于推广(尽管对于这个问题通过计算整个反射可以轻松完成). 但是,微分法却可以用于在
的微分来处置的. Neumann 边界条件利用反射思想来处置,该思想对于一个二阶有限差分逼近来说是可行的,但随阶数的升高,并不易于推广(尽管对于这个问题通过计算整个反射可以轻松完成). 但是,微分法却可以用于在  处Neumann 边界条件的任意阶的差分. 作为一个例子,该问题的一个解将使用四阶差分来得到.
处Neumann 边界条件的任意阶的差分. 作为一个例子,该问题的一个解将使用四阶差分来得到. 求解,这样就可以把离散系统作为一组常微分方程来处理. 通过增加离散边界条件,该方程的解本身就渐进收敛于正确的边界条件,虽然有暂时的偏离或初始条件不一致. 这个可以从它的精确解中看到.
求解,这样就可以把离散系统作为一组常微分方程来处理. 通过增加离散边界条件,该方程的解本身就渐进收敛于正确的边界条件,虽然有暂时的偏离或初始条件不一致. 这个可以从它的精确解中看到. 的默认值是 Automatic,缩放因子
的默认值是 Automatic,缩放因子  用于狄利克雷边界条件,在其他情况下,使用缩放因子
用于狄利克雷边界条件,在其他情况下,使用缩放因子  .
.







 可以很方便地在两种方法之间切换. 应该记住的是,使用 DifferentiateBoundaryConditions->False 并不意味着您可以自由选择积分方法;所需方法必须是一个微分代数方程求解程序.
可以很方便地在两种方法之间切换. 应该记住的是,使用 DifferentiateBoundaryConditions->False 并不意味着您可以自由选择积分方法;所需方法必须是一个微分代数方程求解程序.

 的边界条件上就是这样的情况.
的边界条件上就是这样的情况.







 (4) 及默认设置的 AccuracyGoal 和 PrecisionGoal (对于偏微分方程均为4). 对离散得到的常微分方程组进行积分所用的方法,其自身的误差估计是建立在函数值足够精确的假设基础之上的. 此处估计的目的在于寻找一个空间网格,使得空间误差与局部时间误差(至少在初始条件下)能够保持平衡.
(4) 及默认设置的 AccuracyGoal 和 PrecisionGoal (对于偏微分方程均为4). 对离散得到的常微分方程组进行积分所用的方法,其自身的误差估计是建立在函数值足够精确的假设基础之上的. 此处估计的目的在于寻找一个空间网格,使得空间误差与局部时间误差(至少在初始条件下)能够保持平衡. 和
和  是长度不同的向量,而
是长度不同的向量,而  是一个函数,因此您需要选择一个适当的范数. 如果选择
是一个函数,因此您需要选择一个适当的范数. 如果选择  ,那么您可以在两个向量公有的分量上简单地使用一个缩放后的范数,即所有的
,那么您可以在两个向量公有的分量上简单地使用一个缩放后的范数,即所有的  和
和  的所有的间隔点. 这是一个很好的选择,因为它不需要任何网格之间的插值.
的所有的间隔点. 这是一个很好的选择,因为它不需要任何网格之间的插值. 和
和  的函数,以列表形式给出
的函数,以列表形式给出  和
和  的逼近值. (请注意,尽管下面仅使用了均匀网格,但原则上讲这对于任何网格均适用,不论其均匀与否.)
的逼近值. (请注意,尽管下面仅使用了均匀网格,但原则上讲这对于任何网格均适用,不论其均匀与否.)
 点网格上每隔一个点都在
点网格上每隔一个点都在  点网格上. 因此,为简便起见,您可以使用一个范数,仅比较两个网格的公共点. 由于最终目标是满足绝对和相对公差标准,使用一个缩放的范数是合理的. 缩放时,除了考虑右边的大小,还必须包括网格上
点网格上. 因此,为简便起见,您可以使用一个范数,仅比较两个网格的公共点. 由于最终目标是满足绝对和相对公差标准,使用一个缩放的范数是合理的. 缩放时,除了考虑右边的大小,还必须包括网格上  和
和  相应组分量的大小,因为右边的误差最终包括在
相应组分量的大小,因为右边的误差最终包括在  和
和  中.
中. 的最小值,使得误差估计小于或等于1(因为它基于一个缩放后的范数). 原则上,将有可能使用求根算法,但由于
的最小值,使得误差估计小于或等于1(因为它基于一个缩放后的范数). 原则上,将有可能使用求根算法,但由于  只能是整数,这将由过于复杂而且不得不调整停止条件. 一个较为简单的解决方案是使用 Richardson 外推公式来预测什么样的
只能是整数,这将由过于复杂而且不得不调整停止条件. 一个较为简单的解决方案是使用 Richardson 外推公式来预测什么样的  值是恰当的,并重复预测过程,直到得到适当的
值是恰当的,并重复预测过程,直到得到适当的  .
. ,只要能够满足误差估计即可. 请记住,一切都可以随偏微分方程的演变而改变,因此根本不值得付出过多努力只为初始时间来寻找最佳间隔. 一个简单的解决办法是在新的
,只要能够满足误差估计即可. 请记住,一切都可以随偏微分方程的演变而改变,因此根本不值得付出过多努力只为初始时间来寻找最佳间隔. 一个简单的解决办法是在新的  的预测公式中包括一个额外的大于1的因数. 即使有一个额外的因数,还是可能需要一些迭代来得到一个可接受的值. 但是,它通常使该进程加快.
的预测公式中包括一个额外的大于1的因数. 即使有一个额外的因数,还是可能需要一些迭代来得到一个可接受的值. 但是,它通常使该进程加快. 趋近于
趋近于  . 一种更好的方法是利用这样一个事实:在一个给定的
. 一种更好的方法是利用这样一个事实:在一个给定的  点网格上,拟谱方法为
点网格上,拟谱方法为  . 比较两个网格时,对于
. 比较两个网格时,对于  使用较小的
使用较小的  是合理的. 就确定网格大小这一目的而言,这种做法提供了一种不完美但却充分的估计.
是合理的. 就确定网格大小这一目的而言,这种做法提供了一种不完美但却充分的估计.  时,还要考虑的是,这个值不仅要满足公差条件,还要是计算 FFT 的一个高效率的长度. 在 Mathematica 中,高效率的 FFT 不需要二的幂的个长度,因为 Fourier 命令具有一个内置素因子算法.
时,还要考虑的是,这个值不仅要满足公差条件,还要是计算 FFT 的一个高效率的长度. 在 Mathematica 中,高效率的 FFT 不需要二的幂的个长度,因为 Fourier 命令具有一个内置素因子算法.
 大有帮助. 从2到4的改进通常是最显著的,并且在默认的公差范围内,四阶差分一般不会产生像在更高阶数时所可能出现的大的舍入误差. 拟谱差分往往是一个不错的选择,尤其在具有周期性边界条件时,但如果将它们作为默认设置并不好,原因是它们导致雅克比满矩阵,对于刚性方程生成和求解都可能会非常耗费资源.
大有帮助. 从2到4的改进通常是最显著的,并且在默认的公差范围内,四阶差分一般不会产生像在更高阶数时所可能出现的大的舍入误差. 拟谱差分往往是一个不错的选择,尤其在具有周期性边界条件时,但如果将它们作为默认设置并不好,原因是它们导致雅克比满矩阵,对于刚性方程生成和求解都可能会非常耗费资源. 和
和  点网格,而是
点网格,而是  和
和  点网格. 这是因为,在
点网格. 这是因为,在  点网格上值的生成离不开差值法,而差值法自身会导致误差,但是在
点网格上值的生成离不开差值法,而差值法自身会导致误差,但是在  点网格上的值是现成的,只需间隔取值即可. 这在 Richardson 外推公式中是很容易做的,利用
点网格上的值是现成的,只需间隔取值即可. 这在 Richardson 外推公式中是很容易做的,利用  ,得到
,得到 和
和  的解,计算关于 Sine-Gordon 方程的解的误差估. 由于该函数应用于一个已经构建好的网格上,因此已被定义为一个网格的函数. (注意,正如此处所定义的,这仅适用于偶数长度的网格. 处理奇数长度并不困难,但那样会使函数更加复杂.)
的解,计算关于 Sine-Gordon 方程的解的误差估. 由于该函数应用于一个已经构建好的网格上,因此已被定义为一个网格的函数. (注意,正如此处所定义的,这仅适用于偶数长度的网格. 处理奇数长度并不困难,但那样会使函数更加复杂.)


 被有效地转化为等价的
被有效地转化为等价的  值. 这样只是为了提供方便,因为有时问题的设定与步长能更自然的联系在一起,而不是与离散点的个数. 当给
值. 这样只是为了提供方便,因为有时问题的设定与步长能更自然的联系在一起,而不是与离散点的个数. 当给  和对应的
和对应的  选项指定除了 Automatic 以外的值时,使用的限制条件一般更严格.
选项指定除了 Automatic 以外的值时,使用的限制条件一般更严格. 时,激波宽度与
时,激波宽度与  成正比. 超过95%的变化包含在一个宽度为
成正比. 超过95%的变化包含在一个宽度为  的层内. 因此,如果您选择一半激波宽度的最大步长,总是会有一点在激波的陡峭部分,因而有希望在没有显著振荡的条件下对其进行分辨.
的层内. 因此,如果您选择一半激波宽度的最大步长,总是会有一点在激波的陡峭部分,因而有希望在没有显著振荡的条件下对其进行分辨. 的精确度. 然而,一旦您有足够的点来分辨基本图线,根据 NDSolve::eerr 提示信息中所示的后验误差估计进行预测并非不妥(可再增加10%,因为,说到底它只是一个预测).
的精确度. 然而,一旦您有足够的点来分辨基本图线,根据 NDSolve::eerr 提示信息中所示的后验误差估计进行预测并非不妥(可再增加10%,因为,说到底它只是一个预测).


 ) 较大,陡峭显得并不怎么极端,这个默认的解实际上对前端分辨得相当不错. 因此,应该可以从误差估计来预测,以满足默认公差. 一个简单的缩放参数表明,图线宽度在
) 较大,陡峭显得并不怎么极端,这个默认的解实际上对前端分辨得相当不错. 因此,应该可以从误差估计来预测,以满足默认公差. 一个简单的缩放参数表明,图线宽度在  方向上会比在
方向上会比在  方向上窄
方向上窄  倍. 因此,
倍. 因此, 方向的步长比
方向的步长比  方向的步长大这样一个因数是有道理的,或者最小点数可以相应地小上
方向的步长大这样一个因数是有道理的,或者最小点数可以相应地小上  个因数.
个因数. ,取单值作为外积网格的总点数,另一个是
,取单值作为外积网格的总点数,另一个是  ,它的网格必须在每个维度上显式指定.
,它的网格必须在每个维度上显式指定.  的空间网格点,计算 Burgers 方程在差分阶数为2、4、6和拟谱时的解. 时间准确性和精度公差设定得非常高,所以基本上全部误差均来自空间离散化. 请注意,通过在 NDSolve 中指定
的空间网格点,计算 Burgers 方程在差分阶数为2、4、6和拟谱时的解. 时间准确性和精度公差设定得非常高,所以基本上全部误差均来自空间离散化. 请注意,通过在 NDSolve 中指定  ,只有在
,只有在  的解被保存. 如果没有这种预防措施,更精细的网格(这需要更多的时间步)上的某些解可能用尽可用内存. 即便如此,解的列表还是需要的大量时间来计算.
的解被保存. 如果没有这种预防措施,更精细的网格(这需要更多的时间步)上的某些解可能用尽可用内存. 即便如此,解的列表还是需要的大量时间来计算. 
 处的逼近解的最大空间误差作为网格点数函数的对数坐标图. 在均匀的网格上阶数为2、4和6的有限差分分别显示为红色、绿色和蓝色. 均匀(周期性)间距的拟谱倒数显示为黑色.
处的逼近解的最大空间误差作为网格点数函数的对数坐标图. 在均匀的网格上阶数为2、4和6的有限差分分别显示为红色、绿色和蓝色. 均匀(周期性)间距的拟谱倒数显示为黑色.  毫不奇怪,它对应于NDSolve 默认使用的差分阶数. 如果网格足够精细从而进入渐近收敛的部分,可能像在前面两节中那样通过使用 Richardson 外推法进行一个简单的误差估计,但这是在整体解上,而不是局部误差. 另一方面,计算更多的值并观察图形能够指示您是否在渐近部分.
毫不奇怪,它对应于NDSolve 默认使用的差分阶数. 如果网格足够精细从而进入渐近收敛的部分,可能像在前面两节中那样通过使用 Richardson 外推法进行一个简单的误差估计,但这是在整体解上,而不是局部误差. 另一方面,计算更多的值并观察图形能够指示您是否在渐近部分. 和一个用该差分阶计算得到的解
和一个用该差分阶计算得到的解  的前提下,重新计算该解,其中局部时间公差比所得到的实际空间准确度稍微严格一些,如果该准确度已足够的话. 该函数输出是这样一个列表{网格点数,差分阶,计算所用秒数,重新计算所得解的实际误差}.
的前提下,重新计算该解,其中局部时间公差比所得到的实际空间准确度稍微严格一些,如果该准确度已足够的话. 该函数输出是这样一个列表{网格点数,差分阶,计算所用秒数,重新计算所得解的实际误差}. 

 处的逼近解误差与计算时间的函数关系的对数图. 显示的每个点标明了用于计算解所用的空间网格点的数量. 在均匀网格上阶数为2、4和6的有限差分分别显示为红色,蓝色和绿色. 具有均匀(周期性)间距的拟谱导数用黑色显示. 注意拟谱方法的成本从513到1025大幅跳跃. 这是因为该方法已切换到刚性求解算法,该算法因离散化产生的密集雅可比矩阵而变得非常昂贵.
处的逼近解误差与计算时间的函数关系的对数图. 显示的每个点标明了用于计算解所用的空间网格点的数量. 在均匀网格上阶数为2、4和6的有限差分分别显示为红色,蓝色和绿色. 具有均匀(周期性)间距的拟谱导数用黑色显示. 注意拟谱方法的成本从513到1025大幅跳跃. 这是因为该方法已切换到刚性求解算法,该算法因离散化产生的密集雅可比矩阵而变得非常昂贵. 时,高阶解相当差.
时,高阶解相当差.
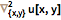
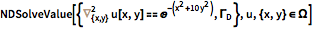

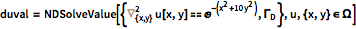









































































No comments:
Post a Comment