漫談不動點定理@ 數學:: 五夢網
www.fivedream.com/page1.aspx?no=221249&step=1&newsno...
漫談不動點定理 江銘輝 五夢網
登山與下山
在未談不動點定理前，我們先談下面一個故事：
有一個數學系的張學生去登山，他從山腳下的一個涼亭出發，沿著一條狹窄的小路，一路觀賞風景，爬到山頂，住在一家旅館裡，假設他從早上七點出發，晚上八點抵達山頂住宿。他的路線是沿者狹窄蜿蜒的小徑，途中的步伐時快、時慢，不一定，中間還有好多次停下來留休息，第二天早上，他開始動身下山，沿著相同的路線，也是早上七時出發，並於晚上八點回到山腳的涼亭，休息。在涼亭休息時，他碰到他的拓樸學教授，梁教授。二人開始閒聊。
登山與下山必有一點時間是相同
梁教授說：「你好，張同學，你這樣昨天上山，今天下山，來回走一趟，你知道在這個行經路線的途中，一定存在一點，洽好是上山的時刻和下山的時刻（譬如5時5分），完全一樣。但我不知道這點在何處，以及是什麼時候？」
張同學：「梁教授，你在跟我開完笑，這絕對不可能的。我二次走路的方式都不一樣，而且有時走快，有時走慢，中間還停下來休閒，吃口糧充飢，或喝飲料解渴。」
梁教授：「儘管你否認，但是站在拓樸學教授的立場，我還是要向你說清楚，講明白。」
梁教授的解釋
於是梁教授拿起筆來畫了如下的圖：
然後梁教授說：「這是一個你昨天登山和今天下山的路徑行程圖，藍色是你從涼亭爬到山頂的路線，紅色是你從山頂下山到涼亭的路徑。你看，你上山與下山的路徑交會於路途中的某一點。雖然我對交會點的時間不清楚，但一定有交會點是無庸置疑。」
梁教授又說：「我們現在換一個方式來講，假設有兩位登山者，同一時間（早上七時），一個往上爬到山頂，另一個往下走到山腳的涼亭。不管他們的速度如何，以及兩人各在途中休息的次數，兩人勢必在某點相會。這個點就是我所說的時間和地點。」
拓樸學的不動點定理
這個故事為拓樸學家所稱的"不動點定理"提供了一個很簡單的例證。它告訴我們至少存在一個這樣的點，並沒告訴我們這個點在什麼地方。
同學們一定對下面這個不動點定理感興趣。這個定理可以這樣來說明:
取一個盒子和一張紙，紙張恰好蓋住盒內的底面。可想而知此時紙上的每個點與正在它下面的盒底上的點配成對。把這張紙拿起來，隨機地揉成一個小球。再把小球扔進盒裡。拓撲學家己經證明，不管小球是怎樣揉成的，也不管它落在盒底的什麼地方，在揉成小球的紙上至少有一個這樣的點，它恰好處在它盒底原來配對點的正上方！
這個定理首先為荷蘭數學家L．E．J．布勞爾在1912年所證明。它具有許多奇妙的應用。例如，由這個定理可以斷言:在任一時刻，在地球上至少有一個地點沒有風。
本文的參考資料：
1. Leonnardo’s Mirror & Other Puzzles Ivan Moscovich 著
Quod Erat Demonstrandum
2008/03/30
從握手到不動點（一）
從握手到不動點（一）
上年，應同學的邀請，我講了一個所謂的數學講座。今年，趁數學周將至，讓我在此也講一些數學。因我希望中一至中七的同學也能看明白，我會盡量詳盡（長氣）地說。
（一）握手定理（Handshaking lemma）
在空間中隨便點一些點，如下
隨意在點與點之間連起線段，如下
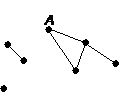
這樣，我們得出一個簡單的圖（graph）。對於圖中的每一點，我們可以定義該點的度數（degree），就是有多少條線由該點引出。參考上圖，因有 2 條線段由 A 點引出，故A 點的度數是 2。把上圖每點的度數寫出來，情況如下：
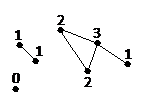
把上圖所有點的度數加起，就是上圖的總度數，即 0 + 1 + 1 + 2+ 3 + 1 + 2 = 10，得到一個偶數（even number）。小習題，試計算下圖的總度數。
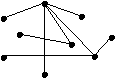
答案是16，也是偶數。現在問：能否畫出一個圖，其總度數是奇數（odd number）？告訴你：不能。這就是所謂的『握手引理』（Hand-Shaking Lemma）：圖的總度數一定是偶數。（換一個講法：奇度數的點之數目必然是偶數。）
這個定理的證明相當簡單，想像圖中的點代表某宴會的出席者，他們在會中彼此握手。如果 A 君和 B 君握手，我們便把對應的 A 點和 B 點連起。所以 A 點的度數，就是 A 君握手的次數。由於 A 君和 B 君握手的同時，B 君和 A 君也在握手，所以數算會中的總握手次數時，必然是算了兩次（double counting），亦即是說，會中的總握手次數必然是偶數，即圖的總度數是偶數。
要欣賞數學之美，其中一個方向是：一些有趣而不直觀的結果，原來可以從一些看來不起眼，非常簡單的原理得到。如此簡單的握手定理，可以推論一個有趣的結果：Sperner 引理。
（二）Sperner 引理
考慮一個大三角形 △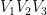
，在三條邊上隨意加點，見下圖。
現在為那些點標號，規則是，
在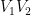
上的點,只能標號 1 或 2；
在
上的點,只能標號 2 或 3；
在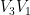
上的點,只能標號 3 或 1。
比如，我們可以有：
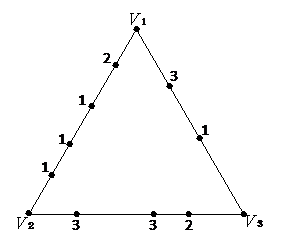
好了，現在大三角形內也隨意加點，亦隨意地為那些點標上 1，2 或 3 的其中一個號碼。同時，頂點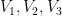
也分別標上 1，2 及 3 三個號碼，見下：
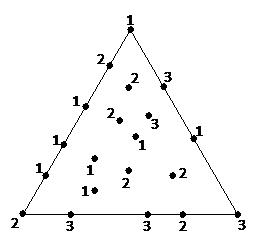
這時，我們可以利用大三角形內的點作頂點，把大三角形劃分為細小的三角形（這過程有稱為三角化 triangulation），見下：
頗亂的圖啊！但原來圖中是隱含『玄機』：就是無論你如何標上號碼，總會出現以『123』為頂點的小三角形，見下：
＂必然存在以『123』為頂點的小三角形＂此之謂 Sperner 引理也。為何會出現這個現象？原來是握手定理。
考慮已細分為若干小三角形的圖，在每個小三角形面上加上一個紅點，見下：
在大三角形外，也補加一個紅點（即上圖的 A 點）。現在把紅點按以下規定連起：若兩相鄰小三角形的公共邊的頂點是『12』，則連起該兩個三角形上的紅點。另外，外點 A 也連到鄰近的紅點，如果 A 和該紅點以頂點是『12』的線段分隔，見下圖。
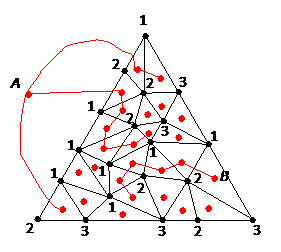
紅色部分，形成了下面的一個圖（graph）
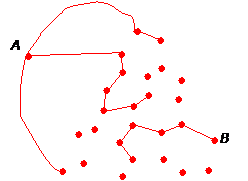
圖中，除 A 點外，紅點的度數只能夠是 0，1 或 2。特別看看 B 點，其度數是 1。看看再上一個圖，B 點是落在以『123』為頂點的小三角形中。不難想出，度數是 1 的點，必然落在以『123』為頂點的小三角形中。換句話說，要證明存在以『123』為頂點的小三角形，即要證明存在度數為 1 的點。
如何證明？看看 A 點，其度數是 3，是奇數。其實，無論如何標號，A 點的度數一定是奇數。因為，在線段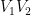 中，以『12』為端點的線段（姑且稱它做＂『12』線段＂）之數目必然是奇數。為何？我們只要想想，在線段 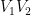上每加多一點，則『12』線段之數目有何改變？我們只能出現以下兩種情況：
(情況A) 該點加在某條『12』線段中，即
這樣，無論加上去的（藍色）點的標號是 1 或 2，我們也沒有增加線段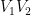 上『12』線段之數目。
(情況B) 該點加在某條頂點標號相同的線段（即『11』線段或『22』線段）中，如果加上去的（藍色）點的標號和線段開端的標號相同，見下圖，則我們也沒有增加線段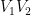 上『12』線段之數目。
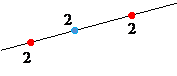
如果加上去的（藍色）點的標號和線段開端的標號不同，見下圖，則我們增加了兩條『12』線段，即線段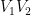 上『12』線段之數目增加了兩條。
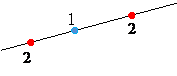
總結上述兩個情況：在線段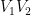 上每加多一點，『12』線段之數目或無增加，或增加兩條。但一開始，未加點的時候，線段 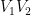其實是一條『12』線段，即『12』線段的數目是1；那麼，無論怎麼加點，『12』線段的數目必然是奇數。
好了，握手定理出場！由剛剛的討論，下圖（是之前出現過的紅色圖）中， A 點的度數是奇數。
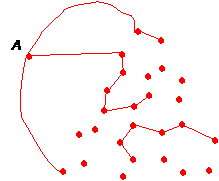
如果圖中沒有一點的度數是 1，則圖的總度數也是奇數（因為除 A 點外，其他點的度數是 0 或 2），這就有違握手定理所指：圖的總度數必是偶數這個事實。亦即是說，度數是 1 的點必然存在；亦即是說，『123』小三角形也必然存在。
想多了解 Sperner 引理，請參考：
http://en.wikipedia.org/wiki/Sperner’s_lemma
好了，我們已經過了兩大關：由握手到 Sperner，還有第三關，我們就看到一個非常漂亮的不動點定理，不過都是下次再談。
P.S. 好想問初中的同學，上面一篇，你看得明嗎？
上年，應同學的邀請，我講了一個所謂的數學講座。今年，趁數學周將至，讓我在此也講一些數學。因我希望中一至中七的同學也能看明白，我會盡量詳盡（長氣）地說。
（一）握手定理（Handshaking lemma）
在空間中隨便點一些點，如下
隨意在點與點之間連起線段，如下
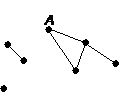
這樣，我們得出一個簡單的圖（graph）。對於圖中的每一點，我們可以定義該點的度數（degree），就是有多少條線由該點引出。參考上圖，因有 2 條線段由 A 點引出，故A 點的度數是 2。把上圖每點的度數寫出來，情況如下：
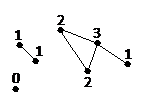
把上圖所有點的度數加起，就是上圖的總度數，即 0 + 1 + 1 + 2+ 3 + 1 + 2 = 10，得到一個偶數（even number）。小習題，試計算下圖的總度數。
答案是16，也是偶數。現在問：能否畫出一個圖，其總度數是奇數（odd number）？告訴你：不能。這就是所謂的『握手引理』（Hand-Shaking Lemma）：圖的總度數一定是偶數。（換一個講法：奇度數的點之數目必然是偶數。）
這個定理的證明相當簡單，想像圖中的點代表某宴會的出席者，他們在會中彼此握手。如果 A 君和 B 君握手，我們便把對應的 A 點和 B 點連起。所以 A 點的度數，就是 A 君握手的次數。由於 A 君和 B 君握手的同時，B 君和 A 君也在握手，所以數算會中的總握手次數時，必然是算了兩次（double counting），亦即是說，會中的總握手次數必然是偶數，即圖的總度數是偶數。
要欣賞數學之美，其中一個方向是：一些有趣而不直觀的結果，原來可以從一些看來不起眼，非常簡單的原理得到。如此簡單的握手定理，可以推論一個有趣的結果：Sperner 引理。
（二）Sperner 引理
考慮一個大三角形 △
，在三條邊上隨意加點，見下圖。現在為那些點標號，規則是，
在
上的點,只能標號 1 或 2；在
上的點,只能標號 2 或 3；在
上的點,只能標號 3 或 1。比如，我們可以有：
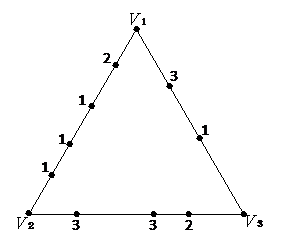
好了，現在大三角形內也隨意加點，亦隨意地為那些點標上 1，2 或 3 的其中一個號碼。同時，頂點
也分別標上 1，2 及 3 三個號碼，見下：這時，我們可以利用大三角形內的點作頂點，把大三角形劃分為細小的三角形（這過程有稱為三角化 triangulation），見下：
頗亂的圖啊！但原來圖中是隱含『玄機』：就是無論你如何標上號碼，總會出現以『123』為頂點的小三角形，見下：
＂必然存在以『123』為頂點的小三角形＂此之謂 Sperner 引理也。為何會出現這個現象？原來是握手定理。
考慮已細分為若干小三角形的圖，在每個小三角形面上加上一個紅點，見下：
在大三角形外，也補加一個紅點（即上圖的 A 點）。現在把紅點按以下規定連起：若兩相鄰小三角形的公共邊的頂點是『12』，則連起該兩個三角形上的紅點。另外，外點 A 也連到鄰近的紅點，如果 A 和該紅點以頂點是『12』的線段分隔，見下圖。
紅色部分，形成了下面的一個圖（graph）
圖中，除 A 點外，紅點的度數只能夠是 0，1 或 2。特別看看 B 點，其度數是 1。看看再上一個圖，B 點是落在以『123』為頂點的小三角形中。不難想出，度數是 1 的點，必然落在以『123』為頂點的小三角形中。換句話說，要證明存在以『123』為頂點的小三角形，即要證明存在度數為 1 的點。
如何證明？看看 A 點，其度數是 3，是奇數。其實，無論如何標號，A 點的度數一定是奇數。因為，在線段
中，以『12』為端點的線段（姑且稱它做＂『12』線段＂）之數目必然是奇數。為何？我們只要想想，在線段 上每加多一點，則『12』線段之數目有何改變？我們只能出現以下兩種情況：(情況A) 該點加在某條『12』線段中，即
這樣，無論加上去的（藍色）點的標號是 1 或 2，我們也沒有增加線段
上『12』線段之數目。(情況B) 該點加在某條頂點標號相同的線段（即『11』線段或『22』線段）中，如果加上去的（藍色）點的標號和線段開端的標號相同，見下圖，則我們也沒有增加線段
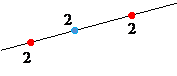
上『12』線段之數目。如果加上去的（藍色）點的標號和線段開端的標號不同，見下圖，則我們增加了兩條『12』線段，即線段
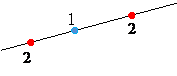
上『12』線段之數目增加了兩條。總結上述兩個情況：在線段
上每加多一點，『12』線段之數目或無增加，或增加兩條。但一開始，未加點的時候，線段 其實是一條『12』線段，即『12』線段的數目是1；那麼，無論怎麼加點，『12』線段的數目必然是奇數。好了，握手定理出場！由剛剛的討論，下圖（是之前出現過的紅色圖）中， A 點的度數是奇數。
如果圖中沒有一點的度數是 1，則圖的總度數也是奇數（因為除 A 點外，其他點的度數是 0 或 2），這就有違握手定理所指：圖的總度數必是偶數這個事實。亦即是說，度數是 1 的點必然存在；亦即是說，『123』小三角形也必然存在。
想多了解 Sperner 引理，請參考：
http://en.wikipedia.org/wiki/Sperner’s_lemma
好了，我們已經過了兩大關：由握手到 Sperner，還有第三關，我們就看到一個非常漂亮的不動點定理，不過都是下次再談。
P.S. 好想問初中的同學，上面一篇，你看得明嗎？
不動點定理與 Hopf 定理 May 16, 2005
Brouwer 不動點定理與 Hopf 定理
- THANXmm -
我個人比較鍾情于拓撲和幾何。 因爲現代的數學研究的是不變量的數學，不變量的性質，而拓撲最能夠體現出不變量的性質，所以拓撲是很美妙的。而Brouwer定理，Hopf定理是我所接觸的結論中非常漂亮的兩個。
兩個光滑流行M,N,如果存在從M到N的光滑映射f，那麽映射的Jacobi矩陣的rank就定義爲映射的rank. 現在，若存在M上一點P,使得對于P點，rank(f)=dim(M),我們說P爲regular point(正則點），並且若q=f(p),則稱q爲映射f的正則值（regular value); 令df(q)爲過q點的切映射，引入符號sign(df(q)),使得若df(q)保定向，sign(df)=1；若df(q)反定向，sign(df) =-1； 定義deg(f;y)爲sign(df(x))的和，x是正則值y的所有逆像點。
現在我首先敘述一下Morse-Sard,Brown定理(符號如前）： Morse-Sard定理：令C爲映射f的不是正則點的點所構成的集合，則f(C)的Lebesgue測度爲 零。 Brown定理：N中的正則值在N中是處處稠密的。
我感覺這兩個定理都是經典分析學中的經典定理，但是現在基本上都是用微分拓撲的方法來證明的。微分拓撲在數學的很多分支中有廣泛的應用，比如代數學基本定理，這個定理雖說是單數學中提出來的，但是在各種證明方法中，竟然沒有一個是純代數性質的。這其實是一個很有趣的事情，同時也說明了，數學的各種分支，本質上是密不可分的。
通過Morse-Sard定理，我們可以證明Brouwer不動點定理：任意從單位圓到自身的光滑映射（實際上條件可以降爲連續映射）都存在不動點。 而且，這個定理有一個深刻的推論，那就是：任意從緊致凸集到自身的光滑映射都存在不動點。
下面再來介紹Hopf定理，先來一些准備工作：令M是一個光滑流行，用X(P)來表示過P點的光滑切向量場，如果X(P)=0,我們稱P點是奇點。 如果還存在P點的鄰域U,使得對于U內任意的q點，都有X(q)!=0,我們稱P點爲孤立奇點。 Hopf定理：如果M是一個緊致定向流行（就是閉流行），X是M上的光滑切向量場，且X僅有孤立奇點，則：1）X至多有有限個奇點，記作：p1,p2,.....,pk 2) deg(f;pk)=E(M);(E爲M的Euler數）；
Hopf定理將拓撲性質與流行的度相聯系，也算是微分拓撲中的一個深刻而經典的定理了。
符號滿天飛，想必大家看到這兒已經暈菜了；所以我想介紹一下上面提到的那些定理的兩個有趣的應用。我們知道RP(n)(n維射影空間）可以寫作S(n)的對徑點粘合f，不妨令f=e(f');其中f':S(n)->S(n),e:S(n)- >RP(n)是對徑點粘合的映射。因爲S(n)是緊致凸集，那麽f'一定有不懂點。而在e的作用下，e(x)=e(-x); 這樣，我們可以證明，一定存在S(n)上的p點，令f(p)=f(-p);
如果我們將地球表面的水平風速看作地球球面上的切向量場X；由于E(球面）=2，于是球面上的連續切向量場有奇點，于是一定存在球面上的P點，使得X(p)=0; 于是我們得到這樣的結論：任何時刻地球上存在一處水平風速爲零。 呵呵呵呵，很有趣的結論吧！！！！(王朝網路 wangchao.net.cn)
No comments:
Post a Comment