 守恆
守恆類氫原子[编辑]
维基百科,自由的百科全书
稱滿足上述系統的薛丁格方程式的波函數為單電子波函數,或類氫原子波函數。類氫原子波函數是單電子角動量算符
 與其 z-軸分量算符
與其 z-軸分量算符  的本徵函數。由於能量本徵值
的本徵函數。由於能量本徵值 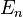 跟量子數
跟量子數  ,
, 無關,而只跟主量子數
無關,而只跟主量子數  有關。所以,類氫原子波函數可以由主量子數
有關。所以,類氫原子波函數可以由主量子數  、角量子數
、角量子數  、磁量子數
、磁量子數  ,獨特地決定。因為構造原理,還必須加上自旋量子數
,獨特地決定。因為構造原理,還必須加上自旋量子數 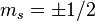 。對於多電子原子,這原理限制了電子構型的四個量子數。對於類氫原子,所有簡併的軌域形成了一個電子層;每一個電子層都有其獨特的主量子數
。對於多電子原子,這原理限制了電子構型的四個量子數。對於類氫原子,所有簡併的軌域形成了一個電子層;每一個電子層都有其獨特的主量子數  .這主量子數決定了電子層的能量。主量子數也限制了角量子數
.這主量子數決定了電子層的能量。主量子數也限制了角量子數  、磁量子數
、磁量子數  、自旋量子數
、自旋量子數  的值域。
的值域。除了氫原子(電中性)以外,類氫原子都是離子,都帶有正電荷量
 ;其中,
;其中, 是單位電荷量,
是單位電荷量, 是原子序數。離子像He+、Li2+、Be3+、B4+、等等,都是類氫原子。
是原子序數。離子像He+、Li2+、Be3+、B4+、等等,都是類氫原子。在元素周期表中,第 IA 族的鹼金屬元素,其原子的最外電子層都有一個電子,而第二外層電子層的亞層,不論是 s 亞層或 p 亞層,凡是內中有電子的亞層.都已被填滿。例如,鈉元素有11個電子。電子排佈為
 。最外層只有一個電子。第二外層的
。最外層只有一個電子。第二外層的  與
與  亞層都已填滿。鉀元素有19個電子。電子排佈為
亞層都已填滿。鉀元素有19個電子。電子排佈為 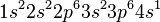 。第二外層的
。第二外層的  與
與  亞層都已填滿。由於
亞層都已填滿。由於  亞層的軌域的能量較高,最外層唯一的一個電子的軌域是
亞層的軌域的能量較高,最外層唯一的一個電子的軌域是  。受到內層電子的緊密屏蔽,這最外層的電子只能感受到大約為一個質子的存在。有效原子序數是 1 。所以,這鹼金屬的單電子系統可以視為一個類氫原子系統。可以用原子序數為 1 的類氫原子波函數,來近似地表達這電子的量子態。
。受到內層電子的緊密屏蔽,這最外層的電子只能感受到大約為一個質子的存在。有效原子序數是 1 。所以,這鹼金屬的單電子系統可以視為一個類氫原子系統。可以用原子序數為 1 的類氫原子波函數,來近似地表達這電子的量子態。因為電子與電子之間的庫侖相互作用,擁有多個電子的原子或離子沒有解析解,必須用數值法來做量子力學計算,才能求得近似的波函數以及其它有關性質。由於哈密頓量的球對稱性,一個原子的角動量
 守恆。許多數值程序,開始於單電子算符
守恆。許多數值程序,開始於單電子算符 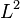 與
與  的本徵函數的乘積。所計算出來的波函數的徑向部分 有時會是數值列表或斯萊特軌域 (Slater orbitals) 。應用角動量偶合方法 (angular momentum coupling) ,可以設定
的本徵函數的乘積。所計算出來的波函數的徑向部分 有時會是數值列表或斯萊特軌域 (Slater orbitals) 。應用角動量偶合方法 (angular momentum coupling) ,可以設定  (或許也可以設定
(或許也可以設定  )的多電子本徵函數。
)的多電子本徵函數。薛丁格方程式解答[编辑]
類氫原子問題的薛丁格方程式為 ;
;
 是約化普朗克常數,
是約化普朗克常數, 是電子與原子核的約化質量,
是電子與原子核的約化質量, 是量子態的波函數,
是量子態的波函數, 是能量,
是能量, 是庫侖位勢:
是庫侖位勢: ;
;
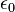 是真空電容率,
是真空電容率, 是原子序,
是原子序, 是單位電荷量,
是單位電荷量, 是電子離原子核的距離。
是電子離原子核的距離。採用球坐標
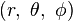 ,將拉普拉斯算子展開:
,將拉普拉斯算子展開:![-\frac{\hbar^2}{2\mu r^2}\left \{ \frac{\partial}{\partial r}\left(r^2 \frac{\partial}{\partial r}\right)+\frac{1}{\sin^2\theta}\left[\sin\theta\frac{\partial}{\partial \theta}\left(\sin\theta \frac{\partial}{\partial \theta}\right)+\frac{\partial^2}{\partial \phi^2}\right]\right \}\psi - \frac{Ze^2}{4 \pi \epsilon_0 r}\psi= E\psi](http://upload.wikimedia.org/math/1/7/4/17419a133f1568d83cc8b8e98b740e65.png) 。
。
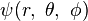 是徑向函數
是徑向函數  與球諧函數
與球諧函數 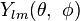 的乘積:
的乘積: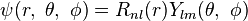 。
。
角部分解答[编辑]
參數為天頂角和方位角的球諧函數,滿足角部分方程式![-\frac{1}{\sin^2\theta} \left[
\sin\theta\frac{\partial}{\partial\theta} \Big(\sin\theta\frac{\partial}{\partial\theta}\Big)
+\frac{\partial^2}{\partial \phi^2}\right] Y_{lm}(\theta,\phi)
= l(l+1)Y_{lm}(\theta,\phi)](http://upload.wikimedia.org/math/4/1/7/4172d3c0d96864ea7d60b8505fb77bcc.png) ;
;
 是軌角動量的角量子數。磁量子數
是軌角動量的角量子數。磁量子數  (滿足
(滿足  )是軌角動量對於 z-軸的(量子化的)投影。不同的
)是軌角動量對於 z-軸的(量子化的)投影。不同的  與
與  給予不同的軌角動量函數解答
給予不同的軌角動量函數解答  :
: ;
;
 是虛數單位,
是虛數單位, 是伴隨勒讓德多項式,用方程式定義為
是伴隨勒讓德多項式,用方程式定義為 ;
;
 是
是  階勒讓德多項式,可用羅德里格公式表示為
階勒讓德多項式,可用羅德里格公式表示為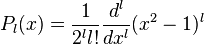 。
。
徑向部分解答[编辑]
徑向函數滿足一個一維薛丁格方程式:![\left[ - {\hbar^2 \over 2\mu r^2} {d\over dr}\left(r^2{d\over dr}\right) +{\hbar^2 l(l+1)\over 2\mu r^2} - \frac{Ze^2}{4 \pi \epsilon_0 r} \right] R_{nl}(r)=ER_{nl}(r)](http://upload.wikimedia.org/math/9/8/4/98457a4d7ff7f64f4508f91d948f824b.png) 。
。
除了量子數
 與
與  以外,還有一個主量子數
以外,還有一個主量子數  。為了滿足
。為了滿足  的邊界條件,
的邊界條件, 必須是正值整數,能量也離散為能級
必須是正值整數,能量也離散為能級  。隨著量子數的不同,函數
。隨著量子數的不同,函數  與
與  都會有對應的改變。按照慣例,規定用波函數的下標符號來表示這些量子數。這樣,徑向函數可以表達為
都會有對應的改變。按照慣例,規定用波函數的下標符號來表示這些量子數。這樣,徑向函數可以表達為![R_{nl} (r) = \sqrt {{\left ( \frac{2 Z}{n a_{\mu}} \right ) }^3\frac{(n-l-1)!}{2n[(n+l)!]^3} } e^{- Z r / {n a_{\mu}}} \left ( \frac{2 Z r}{n a_{\mu}} \right )^{l} L_{n-l-1}^{2l+1} \left ( \frac{2 Z r}{n a_{\mu}} \right )](http://upload.wikimedia.org/math/e/1/8/e18eeb1dbba683e3e9a8880415f247b4.png) ;
;
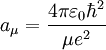 。
。  近似於波耳半徑
近似於波耳半徑 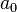 。假若,原子核的質量是無限大的,則
。假若,原子核的質量是無限大的,則 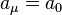 ,並且,約化質量等於電子的質量,
,並且,約化質量等於電子的質量,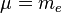 。
。 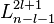 是廣義拉格耳多項式,定義為
是廣義拉格耳多項式,定義為 ;
;
 是拉格耳多項式,可用羅德里格公式表示為
是拉格耳多項式,可用羅德里格公式表示為 。
。
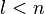 。
。知道徑向函數
 與球諧函數
與球諧函數  的形式,可以寫出整個量子態的波函數,也就是薛丁格方程式的整個解答:
的形式,可以寫出整個量子態的波函數,也就是薛丁格方程式的整個解答: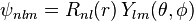 。
。
量子數[编辑]
量子數 ,
, ,
, 都是整數,容許下述值:
都是整數,容許下述值: ,
,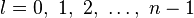 ,
,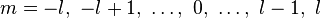 。
。
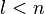 ?為什麼
?為什麼  ?若想進一步知道關於這些量子數的群理論,敬請參閱氫原子量子力學。
?若想進一步知道關於這些量子數的群理論,敬請參閱氫原子量子力學。角動量[编辑]
每一個原子軌域都有特定的角動量向量 。它對應的算符是一個向量算符
。它對應的算符是一個向量算符  。角動量算符的平方
。角動量算符的平方  的本徵值是
的本徵值是 。
。
 。
。
![[\hat{L}^2,\ \hat{L}_z]=0](http://upload.wikimedia.org/math/e/4/8/e4816d7026563c2279a3eec30b995d8c.png) ,
, 與
與  是對易的,
是對易的,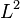 與
與  彼此是相容可觀察量,這兩個算符有共同的本徵態。根據不確定性原理,以同時地測量到
彼此是相容可觀察量,這兩個算符有共同的本徵態。根據不確定性原理,以同時地測量到 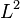 與
與  的同樣的本徵值。
的同樣的本徵值。由於
![[\hat{L}_x,\ \hat{L}_y]=i\hbar \hat{L}_z](http://upload.wikimedia.org/math/3/1/3/313d2413ca14d37ba6a42fc8a8f98157.png) ,
, 與
與  互相不對易,
互相不對易, 與
與 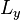 彼此是不相容可觀察量,這兩個算符絕對不會有共同的基底量子態。一般而言,
彼此是不相容可觀察量,這兩個算符絕對不會有共同的基底量子態。一般而言, 的本徵態與
的本徵態與  的本徵態不同。
的本徵態不同。給予一個量子系統,量子態為
 。對於可觀察量算符
。對於可觀察量算符  ,所有本徵值為
,所有本徵值為 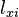 的本徵態
的本徵態 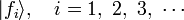 ,形成了一組基底量子態。量子態
,形成了一組基底量子態。量子態  可以表達為這基底量子態的線性組合:
可以表達為這基底量子態的線性組合: 。對於可觀察量算符
。對於可觀察量算符  ,所有本徵值為
,所有本徵值為  的本徵態
的本徵態 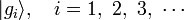 ,形成了另外一組基底量子態。量子態
,形成了另外一組基底量子態。量子態  可以表達為這基底量子態的線性組合:
可以表達為這基底量子態的線性組合: 。
。假若,測量可觀察量
 ,得到的測量值為其本徵值
,得到的測量值為其本徵值 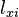 ,則量子態機率地塌縮為本徵態
,則量子態機率地塌縮為本徵態  。假若,立刻再測量可觀察量
。假若,立刻再測量可觀察量  ,得到的答案必定是
,得到的答案必定是 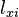 ,在很短的時間內,量子態仍舊處於
,在很短的時間內,量子態仍舊處於  。可是,假若改為立刻測量可觀察量
。可是,假若改為立刻測量可觀察量 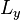 ,則量子態不會停留於本徵態
,則量子態不會停留於本徵態  ,而會機率地塌縮為
,而會機率地塌縮為  本徵值是
本徵值是 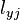 的本徵態
的本徵態  。這是量子力學裏,關於測量的一個很重要的特性。
。這是量子力學裏,關於測量的一個很重要的特性。根據不確定性原理,
![\Delta L_x\ \Delta L_y \ge \left|\frac{\langle[\hat{L}_x,\ \hat{L}_y]\rangle}{2i}\right|=\frac{\hbar |\langle \hat{L}_z\rangle|}{2}](http://upload.wikimedia.org/math/7/b/7/7b7c71d9785f3bb6e7038d889479413a.png) 。
。
 的不確定性與
的不確定性與 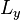 的不確定性的乘積
的不確定性的乘積  ,必定大於或等於
,必定大於或等於 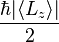 。
。類似地,
 與
與  之間,
之間,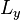 與
與  之間,也有同樣的特性。
之間,也有同樣的特性。自旋-軌道作用[编辑]
電子的總角動量必須包括電子的自旋。在一個真實的原子裏,因為電子環繞著原子核移動,會感受到磁場。電子的自旋與磁場產生作用 ,這現象稱為自旋-軌道作用。當將這現象納入計算,自旋與角動量不再是保守的,可以將此想像為電子的進動。為了維持保守性,必須取代量子數 、
、 與自旋的投影
與自旋的投影  ,而以量子數
,而以量子數  ,
,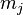 來計算總角動量。
來計算總角動量。精細結構[编辑]
在原子物理學裏,因為一階相對論性效應,與自旋-軌道耦合,而產生的原子譜線分裂,稱為精細結構。非相對論性,無自旋的電子產生的譜線稱為粗略結構。類氫原子的粗略結構只跟主量子數
 有關。可是,更精確的模型,考慮到相對論效應與自旋-軌道效應,能夠分解能級的簡併,使譜線能更精細地分裂。相對於粗略結構,精細結構是一個
有關。可是,更精確的模型,考慮到相對論效應與自旋-軌道效應,能夠分解能級的簡併,使譜線能更精細地分裂。相對於粗略結構,精細結構是一個  效應;其中,
效應;其中, 是原子序數,
是原子序數, 是精細結構常數。
是精細結構常數。在相對論量子力學裏,狄拉克方程式可以用來計算電子的波函數。用這方法,能階跟主量子數
 、總量子數
、總量子數  有關[1][2],容許的能量為
有關[1][2],容許的能量為![E_{nj} = E_n\left[1+\left(\frac{Z\alpha}{n}\right)^2\left(\frac{1}{j+\frac{1}{2}} - \frac{3}{4n}\right)\right]](http://upload.wikimedia.org/math/b/0/4/b04eb0ff22b8c99e00ccf11ca5cc8e52.png) 。
。
參閱[编辑]
參考文獻[编辑]
- ^ French, A.P.. Introduction to Quantum Physics. en:W.W. Norton & Company. 1978: pp. 542.
- ^ 狄拉克方程式關於氫原子的解答
- Tipler, Paul & Ralph Llewellyn (2003). Modern Physics (4th ed.). New York: W. H. Freeman and Company. ISBN 0-7167-4345-0
- Griffiths, David J. Introduction to Quantum Mechanics. Upper Saddle River, NJ: Prentice Hall. 1995: 131–200. ISBN 0-13-111892-7.
No comments:
Post a Comment