维基百科,自由的百科全书
高斯函数的形式为
c2 = 2 的高斯函数是傅立叶变换的特征函数。这就意味着高斯函数的傅立叶变换不仅仅是另一个高斯函数,而且是进行傅立叶变换的函数的标量倍。
高斯函数属于初等函数,但它没有初等不定积分。但是仍然可以在整个实数轴上计算它的广义积分(参见高斯积分):
应用[编辑]
高斯函数的不定积分是误差函数。在自然科学、社会科学、数学以及工程学等领域都有高斯函数的身影,这方面的例子包括:- 在统计学与概率论中,高斯函数是正态分布的密度函数,根据中心极限定理它是复杂总和的有限概率分布。
- 高斯函数是量子谐振子基态的波函数。
- 计算化学中所用的分子轨道是名为高斯轨道的高斯函数的线性组合(参见量子化学中的基组)。
- 在数学领域,高斯函数在埃尔米特多项式的定义中起着重要作用。
- 高斯函数与量子场论中的真空态相关。
- 在光学以及微波系统中有高斯波束的应用。
- 高斯函数在图像处理中用作预平滑核(参见尺度空间表示)。
维基百科,自由的百科全书
原子轨域线性组合,或者简写为LCAO,是量子化学中用于求解分子轨域的一种方法,这种方法是通过对原子轨域进行线性叠加来构造分子轨域。因为它属于分子轨域方法的一种,所以又称原子轨域线性组合的分子轨域方法,或者叫LCAO-MO。它于1929年由Sir John Lennard-Jones引入用于描述元素周期表第一行上原子构成的双原子分子的成键,并且经由Ugo Fano进行了扩展。
在量子力学里,原子的电子组态由波函数来描述。从数学上来看,这些波函数构成了函数基组。在化学反应过程中,轨道波函数会发生改变,根据原子所参与形成的化学键的类型,电子云的形状会相应改变。
LCAO的数学形式为:
 为第
为第 条分子轨道,它被表示为
条分子轨道,它被表示为 个原子基函数(原子轨道)
个原子基函数(原子轨道) 的线性叠加。系数
的线性叠加。系数 表示了第
表示了第 条原子轨道对该分子轨道
条原子轨道对该分子轨道 的贡献大小。
的贡献大小。
作为基函数的原子轨道 通常是在(核)中心场作用下的单电子波函数。所使用的基函数通常是类氢原子,因为类氢原子波函数已知有解析的表达式。当然,基函数也可以选择如高斯函数的其他形式。
通常是在(核)中心场作用下的单电子波函数。所使用的基函数通常是类氢原子,因为类氢原子波函数已知有解析的表达式。当然,基函数也可以选择如高斯函数的其他形式。
通过变分法求系统总能量的最低值,人们可以获得线性展开式前每项的系数 。这种定量方法称为Hartee-Fock方法。但随着计算化学的发展,人们一般不用LCAO做波函数的实际优化,只用其作定性估测,以衡量或预测其他计算方法的结果。
。这种定量方法称为Hartee-Fock方法。但随着计算化学的发展,人们一般不用LCAO做波函数的实际优化,只用其作定性估测,以衡量或预测其他计算方法的结果。
在量子力学里,原子的电子组态由波函数来描述。从数学上来看,这些波函数构成了函数基组。在化学反应过程中,轨道波函数会发生改变,根据原子所参与形成的化学键的类型,电子云的形状会相应改变。
LCAO的数学形式为:
 为第
为第 条分子轨道,它被表示为
条分子轨道,它被表示为 个原子基函数(原子轨道)
个原子基函数(原子轨道) 的线性叠加。系数
的线性叠加。系数 表示了第
表示了第 条原子轨道对该分子轨道
条原子轨道对该分子轨道 的贡献大小。
的贡献大小。作为基函数的原子轨道
 通常是在(核)中心场作用下的单电子波函数。所使用的基函数通常是类氢原子,因为类氢原子波函数已知有解析的表达式。当然,基函数也可以选择如高斯函数的其他形式。
通常是在(核)中心场作用下的单电子波函数。所使用的基函数通常是类氢原子,因为类氢原子波函数已知有解析的表达式。当然,基函数也可以选择如高斯函数的其他形式。通过变分法求系统总能量的最低值,人们可以获得线性展开式前每项的系数
 。这种定量方法称为Hartee-Fock方法。但随着计算化学的发展,人们一般不用LCAO做波函数的实际优化,只用其作定性估测,以衡量或预测其他计算方法的结果。
。这种定量方法称为Hartee-Fock方法。但随着计算化学的发展,人们一般不用LCAO做波函数的实际优化,只用其作定性估测,以衡量或预测其他计算方法的结果。
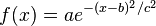


No comments:
Post a Comment