||
费米子和波色子服从完全不同的统计发布, 所以波色子在很低的温度下会占据同一个能级,但是费米子不会,它会像爬楼梯一样由低到高占据所有可能的能级,如下面左图:
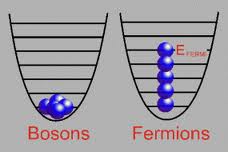
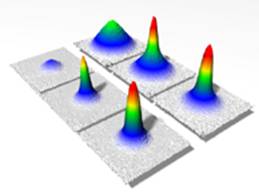
那么为什么费米子会凝聚呢, 如上边右图?所以必须要有相互作用,而且是吸引的相互作用,才能让费米子配对。这是BCS超导理论的核心, 如下图:

大家都玩过这个东西,”飞去来“丢出去以后,它会跑回来。所以在很多情况下,我们用这个原来向初学者或者外行解释BCS超导理论的机理。电子放出一个声子,然后又被另外一个遥远的电子(和原来的电子有相反的动量和自旋)吸收,所以连个没有直接相互作用的电子通过这样的相互作用降低了能量(等价于有了相互作用,或者形成复合子)。我没有办法讲述得更加严格,毕竟是科普类文章。
我接触过一些人,其中有相当一部份人认为,复合子就是波色子,其实不是的。我们定义复合子的算子c=a ks a −ks ′
, 那么我们可以证明[c,c † ]=1−n ks −n −ks ′ ≠1
, 其中,k
, −k
为动量,s
, s ′
为自旋。所以我们看到,其实它不是严格的波色子, 但是它有一些类似波色子的性质。这种复合子的总自旋为s+s ′ =0
(spin is additive), 或者1,从这点来说,它又是一种波色子。
这个问题在BCS理论的原文中解释得非常清楚,如下:

这里有一个概念问题: 自旋为半整数(1/2,3/2…)的粒子统称为费米子,服从费米-狄拉克统计, 整数自旋为波色子,http://baike.baidu.com/view/2447.htm
所以费米子的凝聚也和普通的波色子的凝聚也有所不同。波色子的凝聚是说所有的粒子的波函数完全一样,但是费米子的凝聚是说,复合子的两个费米子的动量k
都不一样,但是它们总的动量都是一样的, 所以凝聚是总动量的凝聚。这也可以从它们的波函数上看出来。
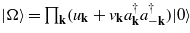
这个也说明,任何两个费米子,只要形成了复合子,都有可能形成凝聚。这个相互作用可以是散射(冷原子中), 电子-声子相互作用(固体中),电子-空穴相互作用(激子)等等。这种费米子凝聚态有些时候也叫做第6态,
http://news.xinhuanet.com/world/2004-12/17/content_2347736.htm
http://ienjoychem.blogspot.hk/2012/07/the-6th-state-of-matter-fermionic.html
(固体液体气体为主要额三态,等粒子体为第四态,波色爱因斯坦凝聚为第五态,费米子凝聚为第六态)。


那么为什么费米子会凝聚呢, 如上边右图?所以必须要有相互作用,而且是吸引的相互作用,才能让费米子配对。这是BCS超导理论的核心, 如下图:

大家都玩过这个东西,”飞去来“丢出去以后,它会跑回来。所以在很多情况下,我们用这个原来向初学者或者外行解释BCS超导理论的机理。电子放出一个声子,然后又被另外一个遥远的电子(和原来的电子有相反的动量和自旋)吸收,所以连个没有直接相互作用的电子通过这样的相互作用降低了能量(等价于有了相互作用,或者形成复合子)。我没有办法讲述得更加严格,毕竟是科普类文章。
我接触过一些人,其中有相当一部份人认为,复合子就是波色子,其实不是的。我们定义复合子的算子
这个问题在BCS理论的原文中解释得非常清楚,如下:

这里有一个概念问题: 自旋为半整数(1/2,3/2…)的粒子统称为费米子,服从费米-狄拉克统计, 整数自旋为波色子,http://baike.baidu.com/view/2447.htm
所以费米子的凝聚也和普通的波色子的凝聚也有所不同。波色子的凝聚是说所有的粒子的波函数完全一样,但是费米子的凝聚是说,复合子的两个费米子的动量
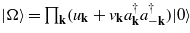
这个也说明,任何两个费米子,只要形成了复合子,都有可能形成凝聚。这个相互作用可以是散射(冷原子中), 电子-声子相互作用(固体中),电子-空穴相互作用(激子)等等。这种费米子凝聚态有些时候也叫做第6态,
http://news.xinhuanet.com/world/2004-12/17/content_2347736.htm
http://ienjoychem.blogspot.hk/2012/07/the-6th-state-of-matter-fermionic.html
(固体液体气体为主要额三态,等粒子体为第四态,波色爱因斯坦凝聚为第五态,费米子凝聚为第六态)。
No comments:
Post a Comment