自爱因斯坦的论动体的电动力在1905年发表以来,在过去的近110年里,科学思想革命性变化的主线条是:
广义相对论引起的科学思想革命
||
自爱因斯坦的论动体的电动力在1905年发表以来,在过去的近110年里,科学思想革命性变化的主线条是:
1. 四维空间(1维时间+三维空间)的偏导数运算【作为联系两点之间的客体变化量(单位长度上的函数变化量),忽略高价小量】,被升级为度规张量变换【作为联系两相邻线段之间的空间客体量】条件下的协变导数运算。而这种升级的客观物理基础就是:时空尺度的变化受到世界线长度客体不变性的制约。
从科学哲学上看,把四维空间的偏导数运算分为两类:一类是满足特定度规张量变换条件的,被看成是反映物理真实性的运算;其它的被划入第二类,不是物理真实的而是纯粹数学上的。这样就压缩了偏导数运算有效性的范畴。
出于这样的一个要点,物理量必须为张量就成为一条科学原理(协变性原理)。质点运动的概念被抛弃,而代之于运动轨迹概念。
2. 度规张量变换既然是客体(或运动),那么不同类别的客体(或运动)就有不同类别的度规张量变换(群变换),由此引出:度规张量变换(群变换)就是物质场(或物质运动),从而,用规范场论重新表达出的物理学就是用普通偏导数表达出的经典物理的升级版本。
引力场理论提供了一个典范,从而也开启了天体科学研究的新时代。由运动轨迹概念升级为流形演化概念。坐标概念被参考流形概念替代。
从科学哲学上看,数学上的流形映射就是物质运动的自然表达方式,从而,对流形映射的属性分类就是对物质运动属性的分类。从此,在科学思想上,摆脱了用直观表象进行物质运动属性分类的束缚,也因此而深入到了物质运动的更深层次。这是革命性的进步,从而也就在原则上能渗入任意学科。
3. 在近半个世纪以来,发现度规张量变换过于狭隘,无法把量子力学包括进来,在经历李代数这个中间环节后,在本世纪初,终于发现,把度规张量变换拓展为群变换后,再限定为超代数下的Clifford几何代数张量,也就可以把量子力学、色动力学也包含进来。而原来用的度规张量变换只是一个特例。
具体的超代数运算法则成为具体的物质抽象运动表述。
由此,又把物质运动的概念拓展为更大的类别,从而为处理复杂运动(复合性的物质运动)提供了理论工具。量子物理的新时代被开启了。
从科学哲学上看,它对流形映射概念加上了更多的限定(同时也扩充了映射的类别),复合属性成为物质运动复杂性的对应描述。原则上,可以完全的实现跨学科的高度抽象性的理论建构。
这就开启了现代物理的大门,也开启了物理学大小统吃的大门。一场科学革命的高潮期似乎是即将到来。
如果一个人无视这一百年来物理学家(作为整体)取得的物理学成就,那么他就只能生活在经典物理的世界里。
如果一个人还在度规张量变换水平上研究物理,发现广义相对论(物理学)的缺陷,他只不过是重复“1.”的线条,而且未必是正确的重复。
如果一个人还在群变换水平上研究物理,发现大量的原理是不足为奇的,他推翻这个原理也好,那个原理也好,总是可能的。但是,那是徒劳无功的。因为,他未必能给自身脱僵的思绪加上必要的束缚,就是加了,也未必加的正确。顶多是在“2.”圈内转来转去而已。
如果不能进入“3.”时代,无论如何叫喊,也是在现代物理的大门之外。
现实就是如此的不以人们的主观愿望而转移。
无论是批广义相对论也好,保广义相对论也好,作为现代物理学革命的导火线,也作为第一个成功的经典型范例,广义相对论作为最重要的环节的历史地位是任何理论和任何人所无法否定的
石墨烯理论(上) | 日志| 果壳网科技有意思
www.guokr.com/blog/768273/
轉為繁體網頁
2014年6月18日 - 在二次量子化的哈密顿量,有如下形式. 这里我们以 ... 此外我们假定近邻原子轨道波函数之间不存在重叠, 也就是说 (紧束缚近似)。格点模型哈密顿 ...轉為繁體網頁
"聲子的二次量子化 "
"我們知道,金屬的電子能帶結構和半導體或絕緣體不一樣,因為電子可以自由運動的導帶和電子參與鍵結的價帶是重疊的,也就是說,金屬內參與鍵結的電子是可以自由運動的導電電子。而金屬內的電子能帶結構有二個重要的物理參數,費米能 (Fermi energy) 和真空能階 (vacuum level),真空能階和費米能的能量差就是所謂的功函數 (work function) 能量。簡單的說,在溫度0K時,費米能是指金屬內的電子佔據的最高能階。也就是說,在溫度0K時,費米能以下,填滿電子,費米能以上,沒有電子。功函數則是金屬內的正電背景離子對電子的淨束縛能,若電子脫離金屬的束縛而躍升至真空能階,自然是變成真空中的自由電子。通常有二種方式可以讓電子獲得額外的能量,脫離金屬的束縛,而躍升至真空能階。一是加熱,電子吸收聲子的能量,產生熱離子放射(thermoionic emission),或是照光,電子吸收光子的能量,產生光電效應。"
欲將固體內的原子的運動處理到二階的近似(即能量對位移的變化是二階),則寫下的 Hamiltonian 具 (13.36) 的形式。為了找出這個 Hamiltonian 所有本徵值的解,
線性彈性學的應用範圍雖然很廣,但還是有不少地方它並不適用。非均勻質材料的問題倒不是什麼根本的困難,因為只要讓(12.2)中 Eabgd 隨空間變化就可以了。然而,連續介質的彈性學在處理波長相當於原子間距的情況時就會發生定性上、本質上的錯誤,即便是在振幅很小的時候也是如此。這種微觀情況下的形變,可藉由考慮晶體子的振動來獲得定量而準確的了解。而聲子的研究則是關於如何分類與命名這些振動模式、如何計算它們的頻率、以及它們如何與機械、電磁或其他力來作用。聲子是晶體中的行進波,許多我們在第七章所學到之處理電子波函數的技術,都可以被直接套用在聲子上。 Born 與 van Karman 所首先提出的關於晶格動力學的第一篇研究結果,事實上比 Laue、Friedrich、Knipping 所獲得的X-光繞射實驗結果更早證明固體乃是由晶格所構成。Bron 回憶大致提到,他們的第一篇文章發表在 Laue 的發現之前。他們之所以對晶格的存在深信不移,是基於有人用格子點的群論分析來解釋晶體的幾何特性,以及稍早有人從晶格理論導出晶體之紅外線振動光譜與其彈性性質的關係。即便是到了 Born 的第二篇文章,仍舊沒有把繞射的結果引入。Born 解釋說晶格的觀念深植在他們心中,因此在當時才把 Laue 的重大的發現僅當作是一個額外的確認。13.2 古典晶格的振動
聲子的研究承續凝集能的研究,這是很自然的,因為兩者都是想知道“想把離子及伴隨的電子在空間中排列成特定的組態,需要花費怎樣的能量代價”。凝集能當然只是要找出能量最小的一個組態,而聲子則是要問把離子自平衡位置作微小的移開需要什麼樣的能量代價。 試想今天我們要決定最低能量組態所會遇到的困難度,想算出 (寫出) 任意離子擺置下的能量 e(u1,u2 ... uN),是相當困難的。有別於像 11.8 節所採取之猜測能量泛函形式的作法,聲子的研究則有賴於假設離子僅偏離了其平衡位置很小的距離,因此能量(13.1)式可泰勒展開成由 u 的次方所組成。 在這樣的條件下, 晶格振動所造成的位能是(13.2),現在符號是假設理想晶體的情況(全整數指標),每個離子由位置 Rl 來標定,且自其偏離的位移向量由 ul 表示,基本上就是要用 u 的次方來表示能量。其中第一項恰是凝集能,可用第 11 章介紹過的方法來算得,但是在本章的討論它是個無關緊要的常數,可以予以忽略。因為這式子是對著最低能量的平衡位置展開,因此 u 的一次項不能存在這式中,最低要從二次開始。式(13.2)裏的 3x3 矩陣 Fll' 則是直接來自能量泰勒展開, 它的表示式是(13.3),這本章非常非常重要的量,又它永遠是個對稱矩陣(想想看為什麼)。週期性邊界條件
我們在電子態研究用了週期性邊條件來簡化推導的工作,同樣的假設與作法也要用來簡化晶格振動的計算。 Fll'ab 只與 Rl-Rl' 有關。整個運動方程式可簡化為(13.14)。 大部分聲子的理論的推導都不需要知道 Fll' 的實際數值大小,因此稍後再介紹如何計算它們。事實上,想從實驗得到這些 Fll' 是不太可能的。 當所有原子都共同移動同一個距離,晶體能量不變,因此 Sl Fll' = 0(13.5)必須滿足。13.2.1 Normal Modes
Normal mode 最重要的特徵是它具有明確的時間週期,它的狀態在一個週期之後會回到原狀。Normal mode 也振動問題的通解(見 (13.6)),將通解代入微分方程式,可以使導數符號消失而獲得相關未知參數的代數關係。例如,(13.6)的通式代入(13.4)之後,可得(13.7a)、(13.7b)。注意這裏出現了 F(k) 的定義,並且形成了由偏振向量 e 與頻率 w 的本徵值問題 [F(k)]e = Mw2e。要不是因為前式是一個三維的問題,(13.7)只要移項一下就解出來了。對每個 k 值而言,因為 F(k) 是實數對稱矩陣(故它是 Hermitian),,它都會有三個互相正交本徵向量 e(即後面提到圖 13.1 時的 e1、e2、e3)。若 ekn (其中 n = 1, 2, 3)是會使 F(k) 對角化的偏振向量,且 Fn 是相對應的本徵值(即對角元素),則馬上可得(13.8) w2ke = Fn(k)/M ,這和一條彈簧的振動頻率等於彈簧常數除以質量是一樣的。大體上來說,三個偏振向量 ekn 分別對應了兩個橫波與一個縱波的振動位向(細節請見課本)。
由於週期性邊界條件的關係,k 所允許的值與 p.137 (6.7) 式所獲得的結果是完全一樣的。除此之外,大家要注意到 (13.7) 式裏所定義 F(k) 的情況下,若 k 再加上任一個倒空間晶格向量 K,只是指數上多了 2pi 的整數倍,因此 (13.9) 式 F(k+K) = F(k) 一定成立。也因此 k 永遠可以被表示成在第一布里淵區之中。晶格震動也就跟電子一樣是通行於週期性位勢的波,同一組波向量可以用來描述或分類兩種波動。
聲子問題與電子問題的其中一個主要差異則是在他們的振動模式的數目。對個別的單電子態而言,一個 晶格所能存在的本徵態的數目是多得沒有限制的,相反的,聲子就有限制,精確地講,只需要在第一個布里淵區內就可以完全窮盡地描述所有可能的聲子態了(回憶對於電子而言,對每一特定 k 值都還有不同能帶“band”n 的差別,而在 reduce zone scheme 就折入到更高的 zone 之中。)此一差異的理由是:電子的波函數在空間中的各點都是有定義的,格子點上與格子點間任意處的波函數都是一樣重要的。然而,聲子態由晶格點上的原子位置就可以完整描述,在兩個原子位置之間,不管如何任意去想像什麼曲線可以把兩個點連起來,其實物理上而言都是沒有區別的。(也就是說,電子態擁有的自由度真的比聲子態的多很多。)範例:一維鏈
考慮一個一維的晶格且原子間交互作用僅達於最鄰近者,則 (13.4) 可簡化成 (13.10),其中 K 相當於彈簧常數。(同學們自己一定要會能導出 (13.10) 式。)把 normal mode 的通解代進入 (13.10) 即得 (13.11) 並可以求出 w,見 (13.12)。若把此結果畫出會看到圖 13.2 的樣子。 圖13.2 有兩個重要的特性之呈現,在更複雜的格子振動也會出現:13.2.2 有 basis 的晶格
(1) 對於小的 k 值,w 正比於 k。這並不意外,只是回複到波長遠大於原子間距離的 (線性) 彈性學而已,而定這條 w(k)線在原點附近的斜率就是聲速。從基本原理來想,對稱性會要求若所有原子都同步位移則晶體能量不變,也因此隨著波長趨於非常長波長的極限,能量 (頻率) 會隨著波數 (k) 的減少而遞減。極長的波長在原子的尺度看來與同步位移差不了多少,因此有較低的能量與振動頻率。(這種類型的激發狀態也叫做 Goldstone mode。) (2) 在接近 zone 的邊界的時候,色散關係(即 w(k) 圖)會彎平下來準備與另一個 zone 相接來滿足週期性的變化。而此一週期性的變化是源自當所有位置位移都被一齊轉換到相距某晶格向量 R0 的格子點上,則因為對稱性的關係此時能量也不會改變的。也就是說這個對稱性可以看成是來自 (13.9),即整個數學問題在 k 超過一個 K 之後就因週期性開始重覆。
範例:有 basis 的一維鏈
前面例子的圖像固然解釋了,在趨近 (線性) 彈性學的極限下,固體的色散關係在小 k 時呈 c |k| 的線性變化(聲速),但這並沒有排除了其他種解 w(k) 的可能性。額外的解會來自當晶胞不再只是簡單的 Bravais 格子,而是裏面還有其他的原子(回顧什麼是 Bravais Lattice,請見第二章。) 有新的原子加入到晶胞內,則格子的自由度就會增加,我們因此可預期要去考慮相對更多的 normal mode 來描述這些額外的自由度。舉例來說,在一個晶胞內有 4 個原子的三維晶體,其每一個 k 值就具有 3 x 4 個normal mode。 低能量的 mode 表現出當 k 小時其頻率正比於 |k| 的行為,被叫做是聲學 mode,這是因為他們隨著 k 值線性增加頻率,且可以被一般的聲音所激發。另有其他的模式存在,當它 k→0,是對應於晶胞內的原子之間互相有接近或遠離的相對變化,而並未跨越晶胞的範圍到下一個鄰近的晶胞。這種振動模式經常是對應到可以被光所激發的能量,因此被叫做是光學 mode。聲學 mode 與光學 mode 的比較可見圖 13.3。 要計算推導有 basis 晶格的 mode,最正規的方法是寫下式 (13.13),我們看到該公式化 (13.4) 多了 n 這個指標,這是用來描述晶胞裏面的 basis 原子(因為現在每個晶胞不只僅有一個原子了)。若我們依循從 (13.4) 導到 (13.7) 的方法,則可得到 (13.14) 與 (13.15) 。以 (13.15) 式的形式乍看之下,要解的數學問題似乎比較模糊不清,然而,只要另定一個指標 p 來把單位晶胞裏的自由度吸收進來,形式就變得清楚了。例如,4 個原子的單胞其 p 就會取值從 1 到 12,其中最前面三個值是第一個原子的 x, y, z 座標,而下三個值則是第二顆的三個座標分量,以此類推。在此一新指標寫法下,(13.15) 式便被改寫成為 (13.16) 的形式,則其作為一個矩陣方程式本徵值問題的數學本質又再度鮮明可解了。
當一個一維鏈有兩種原子,各其質量 M1,M2 ,交替排開。假設每個原子只與最鄰近的原子有交互作用,則運動方程式(對M1與M2 兩種不同的原子)各為如 (13.17a)、(13.17b) 之形式。以 normal mode 的通解形式代入即得 (13.18a)、(13.18b)。這一組聯立微分方程式裏,我們不知道的是 w、e1、e2,而 k 則是一組參數(不同的 k 定出不同的解),k 並不是需要求解的未知數。對 (13.18) 這樣的問題求解,作法是先把它看作是一個線性方程組,未知數是 e1 , e2 。這個線性方程組要有有意義的解(即不是無解或無限解),則其作用在未知向量上的係數矩陣之行列式值要為零(整個問題可先寫成矩陣方程 Ae = 0,而 e 並非零向量,只有 det(A) = 0 一途)。如此要求下會得到一個 w 四次方程式,若只取正解,則可得兩種 w 解,見 (13.19)。 (13.19) 式的兩個解對應於聲子的兩個 branch 的色散關係,畫出來像是圖 13.5 的樣子。隨著 k 值變小頻率變為零的那個是聲學 branch,而另一個頻率比較高的那個叫光學 branch。在 k 很小的情形下,兩個 branch 的解 w(k) , e1 , e2,各具 (13.20a)、(13.20b) 的形式,這驗證了前面所提過了,在聲學模式下,相鄰原子一齊同相移動,而在光學模式下,相鄰原子間作反向相互運動的圖像。範例:鑽石晶格
自己看。結果在圖 13.6。13.3 量子力學晶格的振動
到目前為止的晶格振動都用古典的力學處理。這樣做還能可行的原因是由於量子力學與古典力學在簡諧振子這個系統的結果幾乎是完全一致的,例如它們有相同的頻率。然而,古典力學的振動可有任意振幅,量子力學的則量子化而離散的。對一個波向量 k、偏極化 n 的振動模式,它只能被允許有聲子的二次量子化hwkn(n+1/2) 這樣不連續的能量,見式子 (13.31),其中 n是大於或等於 0 的整數值。當 n=1,則我們說有一個波數是 k 的聲子被激發了。由於任意 n 個聲子可存在 k 這個態,晶格的激發可被看作是滿足 Bose 統計的合群粒子。 雖然古典與量子在分析的結果其形式上只有極小的差異,但量子力學也在好幾個地方對系統的物理性質有關鍵性的影響。例如,在低溫時,晶格振動的振幅可能小於 (13.31) 式所描述的最小值門檻,在那樣的情況下聲子完全不會被激發,則系統的比熱就會與古典所預測的有極大的不同。基於這個理由與其他原因,我們有需要回顧振動的量子力學理論。 對單一個簡諧振子,由 Hamiltonian(13.32)所描述的,我們可以定義上升及下降算子 (13.33a) 及 (13.33b),又叫做創生及湮滅算子。(13.32) 式所 Hamiltonian 可簡化其形式為 (13.34)。另外,原來的“粒子的位置”算子則可以被表示為(13.35)。
欲將固體內的原子的運動處理到二階的近似(即能量對位移的變化是二階),則寫下的 Hamiltonian 具 (13.36) 的形式。為了找出這個 Hamiltonian 所有本徵值的解,我們定義類似 (13.33) 式的 (13.37a) 及 (13.37b)。從這裏可簡單地反推出(見習題 4)如何用這些新定的產生及湮滅算子來表達第 l 顆粒子位移向量 Ul 與其動量 Pl 的關係式,如 (13.38a) 及 (13.38b)。從動量算符與位置算符所具有的對易關係 [Pl, Rl] = -ih作出發,我們可以知道這些湮滅算符滿足 (13.39) 式 [akn, a+kn] = 1 的關係。 再從 (13.37) 推導到 (13.38) 的過程中,頻率 ωkn 與偏極單位向量εkn 原則上是可以任意選取的,只要每個 k 的三個單位向量εkn 自己要正交歸一即可。(大家要深入思考一下這是什麼圖像)然而,最好最理想的選擇當然是要選那些能使 Hamiltonian (13.36) 對角化的方向,也就是這選取 dynamical matrix F 的本徵向量來作 εkn 並且選擇像滿足 (13.8) 關係式中的本徵值來作為 ωkn。另外注意從 (13.7) 我們只知道 Φ(k)=Φ(-k)(這是因為它們兩者只是差一個加總時的次序不同),因此,我們有ωkn =ω-kn 這個 (13.40) 式。 使用 (13.40) 式會給出 (13.41a) 及 (13.41b),為了要得到 (13.41),我們必須用到εkn‧εkn =δnn' 以及εkn‧ε-kn = 0 除非 n=n' 的這兩個關係式。雖然吾人也有完全的自由度來定義εkn 使其具有ε*kn=ε-kn' 的關係,但這會在探索縱波形式的振動時產生混淆,在那種情況(縱波)下,ε*kn= -εkn 才是比較自然的表示法,也因此,在此我們並不假設ε*kn 與ε-kn' 有任何關係。 把 (13.41a) 與 (13.41b) 兩式加起來,這恰好就是 (13.36) 的 Hamiltonian,大家注意到 (13.41a) 與 (13.41b) 各自的第二項會因為此一組合而相消,則 Hamiltonian 竟可成為 (13.42) 這樣的簡單形式。(就像是同時存在的很多振子一樣,而固體的複雜度則是隱藏到 wkn 之 ω與 k 的色散關係裡頭以及各式各樣的本徵振動方向 n 裡面。) 對於單位晶胞內有 basis 原子的晶體,(13.42) 式依舊成立,只不過求和的指標多了對應不同 branch 者,範圍是單位晶胞內所有的原子個數。其實,branch、波向量 k、偏極化 n 可以一起再被吸收到一個指標之內,而有 (13.43) 式之最簡單形式。
什么是二次量子化? - 新华博客- News Blog - 宇宙之父 - 新华网
yzzf.home.news.cn/.../01010047E9640D07F61BDFF7.ht...2014年11月25日 - 二次量子化就是将薛定谔方程或克莱茵-戈登-薛定谔方程、狄拉克方程 ... 它在计算高阶近似项时将出现无穷大,采用重整化技术可以解决这个问题。
轉為繁體網頁[PPT]“高等量子力学”补充专题: 二次量子化简介
staff.ustc.edu.cn/~zjlin/15.01.12.ppt二、量子力学基本理论 ... 全同粒子与交换对称,对称性假设,二次量子化; 混合系综、
轉為繁體網頁密度算符及其时间演化、量子统计 ... 若; |1>和|2>正交,b1和b2是实数,A为厄米算符,且 。 ... 近似方法. 1. 定态微扰理论:非兼并微扰展开(能级不交叉、波函数归一化)、 兼并微扰、变分法(电子结构理论计算); Stark(电场)效应(一级、二级),精细结构(旋 ... 理论物理基础_百度百科
baike.baidu.com/view/4789464.htm2目录编辑. 第1章牛顿力学. 1.1运动律. 1.2行星绕日和万有引力. 1.2.1开普勒定律. 1.2.2 ... 5.3.1玻尔兹曼方程的逐级近似求解. 5.3.2零级 .... 13.4.1二次量子化. 13.4.2
轉為繁體網頁... 现代物理基础丛书:高等量子力学_百度百科
baike.baidu.com/item/现代物理基础丛书:高等量子力学《高等量子力学》共分八章,介绍了二次量子化、相对论量子理论方程、角动量、动力 ... 非自由粒子传播子的近似解法4.2.2两点推论4.2.3非自由粒子传播子的路径积分 ...
轉為繁體網頁石墨烯理论(上) | 日志| 果壳网科技有意思
www.guokr.com/blog/768273/2014年6月18日 - 在二次量子化的哈密顿量,有如下形式. 这里我们以 ... 此外我们假定近邻原子轨道波函数之间不存在重叠, 也就是说 (紧束缚近似)。格点模型哈密顿 ...
轉為繁體網頁量子理论 - 电子信息材料精品课程 - 北京工业大学
qmlab.bjut.edu.cn/edu/syllabus.asp?classid=5量子跃迁:一级近似下的跃迁几率和跃迁率。 ... 主要讲述二次量子化方法定义及基本物理思想、二次量子化后的Hamiltonian表述形式、多体波函数和场算符、自由 ...
轉為繁體網頁什么是二次量子化? - 国科社区 - 国家科技成果网
blog.tech110.net › 王为民的博客 › 日志2014年11月25日 - 这套办法,就是二次量子化。它在计算高阶近似项时将出现无穷大,采用重整化技术可以解决这个问题。由这套方法计算的电子自旋磁矩在小数点 ...
轉為繁體網頁算符二次量子化形式的一种导出方式--《大学物理》2015年01期
www.cnki.com.cn/.../CJFDTotal-DXWL201501003.htm
轉為繁體網頁由 任政学 著作 - 2015二次量子化粒子数表象力学量算符跃迁算符. ... 1, 魏义永;简并微扰论的二级近似公式[J];安徽教育学院学报;2003年03期. 2, 魏健文;多电子原子Thomas修正探讨[J]; ... phymath999: 经二次量子化后得到声子(phonon)的概念二次 ...
phymath999.blogspot.com/2015/03/phonon.html2015年3月23日 - 科学网—二次量子化- 殷桂琴的博文- 科学网—博客 .... 薛定谔方程其实是狄拉克方程在光速无限大时的近似,所以狄拉克方程才 ...... 即在P点附近的的二级小量可忽略的小区域内近似为常数,我们已经知道, 为常数的区域是平坦的。
轉為繁體網頁
n态的(无穷小)空间平移:动量是平移的生成元+量纲考虑à坐标与动量的对易关系,坐标表象、动量表象
n态的(无穷小)时间演化:H是时间演化的生成元+量纲考虑à时间演化算符与含时薛定谔方程(能量本征态à定态薛定谔方程);薛定谔/海森堡绘景à海森堡运动方程;传播子与经典作用量的路径积分à费曼路径积分方法
n态的(无穷小)转动:角动量是转动的生成元+量纲考虑+转动算符的群性质à角动量对易关系,角动量的本征值与本征态
n力学量随时间的变化、能量守恒(能量表象)、对称性与守恒律
n全同粒子与交换对称,对称性假设,二次量子化
n混合系综、密度算符及其时间演化、量子统计力学
n电子的相对论运动方程:狄拉克方程
X
Table I. Some Trends in Path Integration
豆瓣小组
石墨烯理论(上)
Author:
 二维石墨烯
二维石墨烯
石墨烯是由碳原子排列成六边形结构而形成,可以看作每个晶胞中有一个以两个原子为基础的三角结构。晶格向量可以写成


*石墨烯晶体简化结构,石墨烯一个原胞中包含两个不等价的碳原子 ,
, 。其中
。其中 为原胞基矢;
为原胞基矢;
 是晶格常数。下边给出晶格的倒格矢
是晶格常数。下边给出晶格的倒格矢


石墨烯特别重要的物理性质是 ,
, 两个点在石墨烯Brillouin区(
两个点在石墨烯Brillouin区( )顶点处。这些点之所以会被命名为Dirac点的原因,后面将会给予解释。它们在动量空间中位置(倒格矢)为石墨烯第一Brillouin区示意图,其中
)顶点处。这些点之所以会被命名为Dirac点的原因,后面将会给予解释。它们在动量空间中位置(倒格矢)为石墨烯第一Brillouin区示意图,其中  为倒格矢量,
为倒格矢量, ,
,  和
和 是高对称点。
是高对称点。

实空间中三个最邻近矢量

六个次邻近点距离矢量为

对石墨烯的周期六角格点系统采用电子紧束缚模型,只考虑到最近邻原子之间的相互作用,电子可以跳到的最邻近原子。在二次量子化的哈密顿量,有如下形式

这里我们以最低准粒子激发能量 为能量参照点扣除掉它归入本底,即选取
为能量参照点扣除掉它归入本底,即选取 。此外我们假定近邻原子轨道波函数之间不存在重叠, 也就是说
。此外我们假定近邻原子轨道波函数之间不存在重叠, 也就是说 (紧束缚近似)。格点模型哈密顿量便写为
(紧束缚近似)。格点模型哈密顿量便写为

Nambu表象下可写出BdG矩阵:

在晶格A 上 处有自旋
处有自旋 ,
, (
( )将会湮灭(产生)一个电子(对于点B处等价定义也适用),
)将会湮灭(产生)一个电子(对于点B处等价定义也适用), 是最邻近跃迁能量(不同晶格之间的跃迁),
是最邻近跃迁能量(不同晶格之间的跃迁), 表示只对邻近格点原子求和。实际上哈密顿量中
表示只对邻近格点原子求和。实际上哈密顿量中 ,根据上图所示近邻原子之间的相对坐标,计算相邻两个原子的波函数对哈密顿量的重叠积分
,根据上图所示近邻原子之间的相对坐标,计算相邻两个原子的波函数对哈密顿量的重叠积分 可得到
可得到 :
:

则动量表象中哈密顿量为

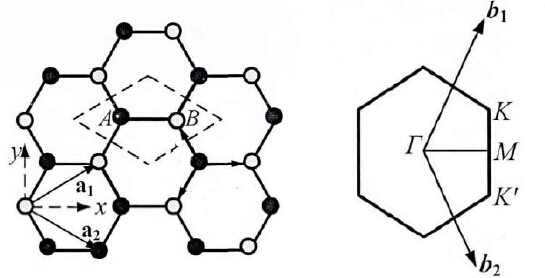
由此可以算出色散关系为:


加号对应较高频能谱 ( ),减号对应较低频能谱(
),减号对应较低频能谱( )。从能谱可以明确看到石墨烯沿着高对称点的色散关系。我们可以看到导带和价带是对称的并且导带和价带在布里渊区的顶角
)。从能谱可以明确看到石墨烯沿着高对称点的色散关系。我们可以看到导带和价带是对称的并且导带和价带在布里渊区的顶角 处是简并的。由于每一个晶胞中有两个碳原子,每一个碳原子都贡献一个
处是简并的。由于每一个晶胞中有两个碳原子,每一个碳原子都贡献一个 电子,因此石墨烯的价带刚好填满同时导带全空,也就是说Fermi面刚好要处在导带和价带之间,由于导带底和价带顶刚好交于
电子,因此石墨烯的价带刚好填满同时导带全空,也就是说Fermi面刚好要处在导带和价带之间,由于导带底和价带顶刚好交于 点,Fermi面应穿过
点,Fermi面应穿过 点,因此我们可以认为石墨烯是一个零带隙的半导体。这主要是对称性的要求,因为晶格格点处
点,因此我们可以认为石墨烯是一个零带隙的半导体。这主要是对称性的要求,因为晶格格点处 和
和 都占据着碳原子,有相同的轨道能级。如果零温,在零能周围能谱是对称的;对于有限温度
都占据着碳原子,有相同的轨道能级。如果零温,在零能周围能谱是对称的;对于有限温度 ,电子-空穴对称性被破坏,
,电子-空穴对称性被破坏, 和
和 带变得不对称。要了解这个高度对称的
带变得不对称。要了解这个高度对称的 附近电子行为,我们不妨靠近一个Dirac点去观察能带结构(在Brillouin区
附近电子行为,我们不妨靠近一个Dirac点去观察能带结构(在Brillouin区 ,
, 点)。也就是说将色散关系围绕
点)。也就是说将色散关系围绕 点展开:在
点展开:在 和
和 附近,且
附近,且

其中 是相对于Dirac点的动量,
是相对于Dirac点的动量, 是Fermi速度,
是Fermi速度,  。这与通常情况
。这与通常情况  ,的区别在于(m 是电子质量)石墨烯中的Fermi速度不取决于能量或动量;而通常情况下我们有
,的区别在于(m 是电子质量)石墨烯中的Fermi速度不取决于能量或动量;而通常情况下我们有 ,即速度的变化取决于能量。这些特点与介质中的光子或者是声子类似,在这些高度对称的点处附近载流子的有效静质量为零,Fermi速度可以和光速相比较,呈现出相对论特性,需要通过Dirac方程来处理(此内容作为重点稍后介绍)。因此我们把这些高度对称的
,即速度的变化取决于能量。这些特点与介质中的光子或者是声子类似,在这些高度对称的点处附近载流子的有效静质量为零,Fermi速度可以和光速相比较,呈现出相对论特性,需要通过Dirac方程来处理(此内容作为重点稍后介绍)。因此我们把这些高度对称的 点称之为Dirac点。
点称之为Dirac点。
同理,假如要考虑次近邻原子的相互作用,定义以 原子为中心的六个最近邻的
原子为中心的六个最近邻的 原子的坐标为
原子的坐标为 ,通过上述类似方法计入次邻近跃迁
,通过上述类似方法计入次邻近跃迁  代入的能量本征方程,我们可以得到能带色散关系
代入的能量本征方程,我们可以得到能带色散关系


我们发现次近邻原子的引入,破坏了能带结构的对称,此时导带和价带不再对称,主要是因为次近邻原子的引入相当于引入了晶格格点轨道能级,因此近邻格点的引入使得Dirac点发生移动。
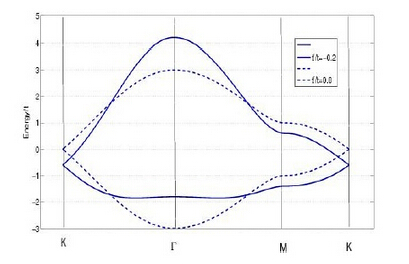
从色散关系我们能够看到次近邻原子的引入改变了Dirac点位置,破坏了电子空穴对称。另外我们发现,能量简并度与动量在动量空间的夹角有关(注意,展开直到 阶,色散关系都取决于动量空间的方向),引入次近邻格点后,Dirac点附近形成三重简并,这就是所谓电子光谱的三角形变。从图中可以看到,次近邻格点的引入并没有破坏Dirac点,也就是说在这些Dirac点处导带低和价带顶仍然简并。很明显考虑次近邻原子相互作用之后Dirac点有向下移动的趋势,即Dirac点处存在能量上
阶,色散关系都取决于动量空间的方向),引入次近邻格点后,Dirac点附近形成三重简并,这就是所谓电子光谱的三角形变。从图中可以看到,次近邻格点的引入并没有破坏Dirac点,也就是说在这些Dirac点处导带低和价带顶仍然简并。很明显考虑次近邻原子相互作用之后Dirac点有向下移动的趋势,即Dirac点处存在能量上 的转移,这是因为我们认为次近邻原子之间电子的跃迁能量是负的原因。一如前面的条件,将方程绕着Dirac点展开,精确到二级项,Dirac点K附近处能带色散关系为
的转移,这是因为我们认为次近邻原子之间电子的跃迁能量是负的原因。一如前面的条件,将方程绕着Dirac点展开,精确到二级项,Dirac点K附近处能带色散关系为
其中 是动量分量间夹角。
是动量分量间夹角。

 无质量Dirac费米子
无质量Dirac费米子
 时电子算符作Fourier级数展开如下:
时电子算符作Fourier级数展开如下:

其中 是单元晶格的数量。我们把
是单元晶格的数量。我们把 由
由 和
和 点电子算符Fourier级数线性组合表示。这产生了一个
点电子算符Fourier级数线性组合表示。这产生了一个 的近似表示,写作:
的近似表示,写作:


 这些新的区域是在假设晶胞绝热变化的情况下,其中指标
这些新的区域是在假设晶胞绝热变化的情况下,其中指标 是指
是指 和
和 点。
点。
简明起见,我们先根据之前在动量表象下的哈密顿量来推导,在 点附近小动量展开
点附近小动量展开


去除一个无关紧要的相位因子 即可得到Dirac电子的有效哈密顿量
即可得到Dirac电子的有效哈密顿量 。
。
在紧束缚时,有效哈密顿量为:




二维Pauli矩阵向量 ,同样抹除无关相位因子就得到标准形式:
,同样抹除无关相位因子就得到标准形式:

有效哈密顿量由两个无质量Dirac粒子(一个在 附近带动量
附近带动量 ,另一个则是
,另一个则是 附近动量
附近动量 )的哈密顿量组成。
)的哈密顿量组成。
二分量旋量电子波函数在 点附近,遵守二维Dirac方程
点附近,遵守二维Dirac方程

在动量空间中, 附近的动量的波函数具有如下形式
附近的动量的波函数具有如下形式

 ,
, 表示对应的本征能量
表示对应的本征能量  ,分别为
,分别为 和
和 带。
带。
 附近动量波函数则有如下形式
附近动量波函数则有如下形式

 ,
, 和
和 点处波函数与时间反演对称性有关:如果
点处波函数与时间反演对称性有关:如果
我们把坐标原点定在 的
的 点处,时间反演变为一个沿着
点处,时间反演变为一个沿着 轴的反射,就是
轴的反射,就是 。还需要注意的是,如果相位
。还需要注意的是,如果相位 的旋转周期是
的旋转周期是 (Berry相位)。相在
(Berry相位)。相在 下的旋转是旋量的特性,事实上,波函数是二分量自旋波函数。一个用来描述本征函数的相关量是他们沿旋转方向的螺旋度,定义为动量算符的投影。量子力学的螺旋度算符有如下形式:
下的旋转是旋量的特性,事实上,波函数是二分量自旋波函数。一个用来描述本征函数的相关量是他们沿旋转方向的螺旋度,定义为动量算符的投影。量子力学的螺旋度算符有如下形式:
现在对于 的定义很明确了,因为
的定义很明确了,因为 也是
也是 的本征态,
的本征态,
 ;
; 的本征方程也类似。
的本征方程也类似。
 双层石墨烯
双层石墨烯
由紧束缚近似方法可将单层石墨烯推广到多层石墨烯系统,乃至叠堆成三维石墨结构。最简单的是双层石墨烯结构,这种结构可以在导带和价带间打开一个能隙。

紧束缚近似哈密顿量写为


 表示在
表示在 平面层晶格
平面层晶格 (
( )中
)中 处消灭一个自旋为
处消灭一个自旋为 的电子。跃迁参数为:
的电子。跃迁参数为: 是面内跃迁能量,
是面内跃迁能量, 是原子
是原子 间的跃迁能量,
间的跃迁能量, 是原子
是原子 间的跃迁能量,
间的跃迁能量, 连接
连接 。
。
在扩大Brillouin区中考察动量接近 点,并忽略
点,并忽略 ,获得有效哈密顿量。
,获得有效哈密顿量。


其中 ;这里引入外场
;这里引入外场 ,大小是两层间化学势位移的一半(相当于在两层之间加一个偏置势场),Nambu四分量旋量为
,大小是两层间化学势位移的一半(相当于在两层之间加一个偏置势场),Nambu四分量旋量为
求解可得到对称能谱图

若 ,
, ,则可以消除高能微扰得到有效哈密顿量
,则可以消除高能微扰得到有效哈密顿量

哈密顿量中 时,有与
时,有与  处比较,
处比较, 为两个抛物线能带
为两个抛物线能带
,能谱是电子-空穴对称的。有两个额外的能带在 处。此处态密度近似恒定,双层石墨烯表现出金属性。由于引入了三角失真,
处。此处态密度近似恒定,双层石墨烯表现出金属性。由于引入了三角失真, 能谱在低能处发生质的变化(注意这个三角失真并不像前面介绍的产生在低能处的较大的动量)。电子-空穴的对称性是保留的,但是我们获得了三条类似Dirac线性能带(并非是
能谱在低能处发生质的变化(注意这个三角失真并不像前面介绍的产生在低能处的较大的动量)。电子-空穴的对称性是保留的,但是我们获得了三条类似Dirac线性能带(并非是 处两个交叉的能带)。一个Dirac点在
处两个交叉的能带)。一个Dirac点在 和
和  处,其他三个点也在
处,其他三个点也在  处,以有限的动量排列在三个等价点。在稳定点处,用拓扑数来看,能带交叉是可以理解的。在一个平面上,一个点周围的封闭曲线的圈数是一个整数,代表总的次数,曲线围绕着这个点逆时针旋转,所以波函数保持不变。在两个抛物线能带接近处 (
处,以有限的动量排列在三个等价点。在稳定点处,用拓扑数来看,能带交叉是可以理解的。在一个平面上,一个点周围的封闭曲线的圈数是一个整数,代表总的次数,曲线围绕着这个点逆时针旋转,所以波函数保持不变。在两个抛物线能带接近处 ( ),这个点的缠绕数为
),这个点的缠绕数为 ;在
;在 ,缠绕数为
,缠绕数为 处和三个Dirac点在
处和三个Dirac点在 ,缠绕数为
,缠绕数为 处,三角扭曲量
处,三角扭曲量 分割成一个Dirac点。一个平面内的旋转或者单层内与其他有关的小旋转,当缠绕数为
分割成一个Dirac点。一个平面内的旋转或者单层内与其他有关的小旋转,当缠绕数为 时,分割了
时,分割了 并且简并入两个Dirac点。外场
并且简并入两个Dirac点。外场 打破了双层的等价、反演对称。这种情形下,色散关系变为
打破了双层的等价、反演对称。这种情形下,色散关系变为

所引起的色散关系如前面的能谱图,和打开的能隙接近,但是并不直接在 点。对于较小的动量,
点。对于较小的动量, ,导带可以扩大
,导带可以扩大
将 换成
换成 可以获得价带色散,双层的在
可以获得价带色散,双层的在 处有能隙。
处有能隙。
 量子Hall效应
量子Hall效应
1.石墨烯中的整数量子Hall效应
人们最开始着研究的量子Hall效应有效能带理论,是从石墨烯晶格开始。对于IQHE,Haldane于1988年发表的PRL中构造的模型是石墨烯晶格加上均匀磁场。石墨烯是个二维晶格,经过上面的介绍,我们知道了石墨烯能带是Dirac锥,可以产生无能隙激发——无质量Dirac费米子。在低能有效理论中,哈密顿量是Dirac形的,解出两条能带:价带和导带,它在Dirac点接触,能谱是线性的。我们在这里对Dirac哈密顿量用另一种形式重新表述——Bloch矢量;因为我们知道对于二能级系统,其Bloch矢可以画出一个Bloch球面(类比于自旋系统,这种矢量可以称为“赝自旋”)。这里Dirac点附近二能带模型的Bloch也可以类似地用这种办法写出来:

其中Pauli矩阵 ,Bloch矢
,Bloch矢  ,由于不加外场时石墨烯具有时间反演对称性
,由于不加外场时石墨烯具有时间反演对称性 :
:  以及结构反演对称性
以及结构反演对称性 :
: ,因此
,因此 。我们熟悉这个情况下的准粒子激发态是无能隙的,也就是有效质量为零 。而在加入磁场项时候,时间反演对称破坏,
。我们熟悉这个情况下的准粒子激发态是无能隙的,也就是有效质量为零 。而在加入磁场项时候,时间反演对称破坏, ,产生非零的质量项。
,产生非零的质量项。
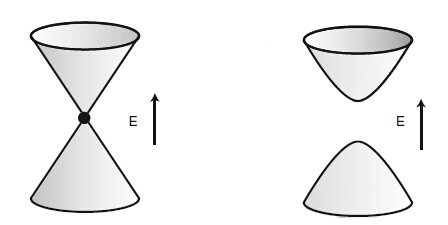
哈密顿量为
有效质量项使得能谱打开能隙:
这时候无限大晶格系统从导体变成绝缘体,这是参数引起的相变。当进一步考虑有限晶格系统时候,我们会计算得到边缘态(表面态)。为此我们考察半无限晶格系统,在 方向上半有界(晶格
方向上半有界(晶格  ),使得边缘或表面为了反映晶格系统内部与真空的势能差异,我们简单地设定质量项为
),使得边缘或表面为了反映晶格系统内部与真空的势能差异,我们简单地设定质量项为 的函数
的函数 
从Dirac方程可以得到波函数旋量解:
 方向的能谱
方向的能谱  ,易见此态几乎限制在边界
,易见此态几乎限制在边界  附近,在边界左右两边都呈指数衰减,因此是边缘态。
附近,在边界左右两边都呈指数衰减,因此是边缘态。
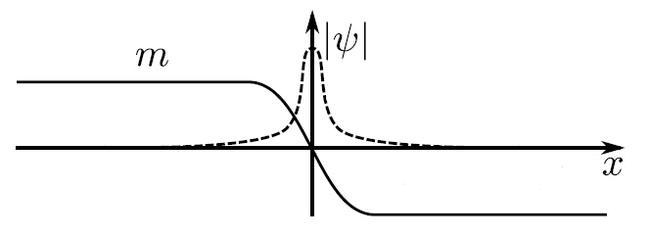
而且此边缘态具有手征性,这一点可以计算其沿着边界上的群速度 知道边缘态模是单向(右手)运动。还发现它是无能隙模,过Fermi面,也就是在Dirac点处。
知道边缘态模是单向(右手)运动。还发现它是无能隙模,过Fermi面,也就是在Dirac点处。
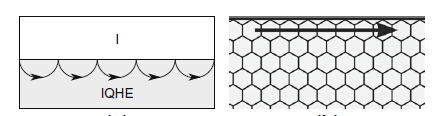
根据TKNN四人的工作,量子Hall电导可以通过计算第一陈类得到,拓扑能带理论的核心在于Brillouin区上的Berry相位。Bloch态在规范变换下不变 ,Berry相来源于波函数内禀的相位任意性,是反映系统拓扑性质的一种几何相位。类比于电磁场规范变换理论,可以定义 Berry联络:
,Berry相来源于波函数内禀的相位任意性,是反映系统拓扑性质的一种几何相位。类比于电磁场规范变换理论,可以定义 Berry联络: 
我们需要对动量空间的几何性质进行考察 ,二维方形晶格 晶格系统,周期性边界条件为:
晶格系统,周期性边界条件为: ;所以二维Brillouin区可以同胚映射成环面,这是一种拓扑紧致化手段。这样,Brillouin区亏格为1。
;所以二维Brillouin区可以同胚映射成环面,这是一种拓扑紧致化手段。这样,Brillouin区亏格为1。

Berry相位就是Berry联络在动量空间 上作闭回路
上作闭回路 的积分;由Stokes定理,它又是Berry曲率对整个Brillouin区作积分:
的积分;由Stokes定理,它又是Berry曲率对整个Brillouin区作积分:

那么Berry曲率为 ,这一套联络都和电磁场理论相似。现在来对这个二维Brillouin区(为了简便设晶格常数为一)的Berry相位(第一陈数):
,这一套联络都和电磁场理论相似。现在来对这个二维Brillouin区(为了简便设晶格常数为一)的Berry相位(第一陈数):



周期性晶格势场中Bloch态在一个倒格矢周期上最多只差一个相因子,因此边界关系为: ,
,

石墨烯Brillouin区是六边形,或以倒格子原胞看是菱形四边形,情况类似。

联络分量为


Berry相位为

由Brillouin区边界上波函数的相位关系:

可最终得到:
由波函数的单值性,则相位差取值只能是 的整数倍,
的整数倍,

此即Berry相位取值,这就解释了能带填满时候Hall电导出现整数量子化现象。在无磁场时候没有Hall效应,相因子相同,故 ; 加入磁场后相当于Brillouin区环面的洞中有磁通形成“环形电流”,由此跨过一个Brillouin区将得到规范相位
; 加入磁场后相当于Brillouin区环面的洞中有磁通形成“环形电流”,由此跨过一个Brillouin区将得到规范相位 (Peierls substraction),当穿过每个Brillouin区的磁通为一个磁通量子大小
(Peierls substraction),当穿过每个Brillouin区的磁通为一个磁通量子大小 时,陈数
时,陈数 。
。

前面提过由于Bloch态具有 规范,因而Berry相位在作
规范,因而Berry相位在作  规范变换时候不变,因此也是个规范不变量。以微分几何语言描述就是一个以
规范变换时候不变,因此也是个规范不变量。以微分几何语言描述就是一个以  流形的Brillouin区为底空间的U(1)丛的第一陈数,是个具有拓扑不变性的整数。此时其规范相因子
流形的Brillouin区为底空间的U(1)丛的第一陈数,是个具有拓扑不变性的整数。此时其规范相因子 相当于纤维的坐标。
相当于纤维的坐标。
在有磁场时形成的量子Hall相之后,多出了一条无能隙边缘态连接导带和价带使得Brillouin流形重构。
这时候Brillouin区的几何流形是Möbius带,陈数就从原来普通环面的零变成了一 ,这也就是量子Hall电导的填充数。
用陈类对量子Hall态分类的思想对应于数学上用Euler示性类对二维紧致定向流形分类:Berry曲率对应于Gauss曲率,第一陈类对应于Euler示性类,那么 流形上的积分就对应于Gauss-Bonnet定理
流形上的积分就对应于Gauss-Bonnet定理

这里 是无边界二维流形
是无边界二维流形  的 Gauss曲率,
的 Gauss曲率, 就是Euler示性数,
就是Euler示性数, 是亏格。
是亏格。
现在我们用另一个角度描述Berry相位。我们记得这节开头之所以用Bloch矢量 来表示哈密顿量,其实就是作铺垫为了现在来以更几何、物理的角度看待描述Berry相位这个拓扑不变量。我们需要从动量空间的Brillouin区映射到赝自旋Bloch球面生成的参数空间(又称为靶空间)。这时我们从上面讨论能带计算的结果知道石墨烯系统哈密顿量特征值是
来表示哈密顿量,其实就是作铺垫为了现在来以更几何、物理的角度看待描述Berry相位这个拓扑不变量。我们需要从动量空间的Brillouin区映射到赝自旋Bloch球面生成的参数空间(又称为靶空间)。这时我们从上面讨论能带计算的结果知道石墨烯系统哈密顿量特征值是  ,Bloch矢就是
,Bloch矢就是 刻画的靶空间里面从单位球中心指向球面的单位矢量
刻画的靶空间里面从单位球中心指向球面的单位矢量 ,而靶空间就是所谓底空间。而Berry相位则是这个单位矢量在球面上所画的闭路劲
,而靶空间就是所谓底空间。而Berry相位则是这个单位矢量在球面上所画的闭路劲 围出的面积所对应的一半立体角
围出的面积所对应的一半立体角  (Bargmann不变量) ,这也是
(Bargmann不变量) ,这也是 流形上的和乐群元,这就是Berry相位被称几何相位的原因。我们可以更浅显地描述:
流形上的和乐群元,这就是Berry相位被称几何相位的原因。我们可以更浅显地描述: 上的切矢经球面上闭合曲线
上的切矢经球面上闭合曲线  平行移动后回到原处,这时我们看到由于曲面的曲率而使得切矢改变方向形成一定夹角。这样我们就需要定义平移产生的联络,以1-形式写出来就是Berry联络
平行移动后回到原处,这时我们看到由于曲面的曲率而使得切矢改变方向形成一定夹角。这样我们就需要定义平移产生的联络,以1-形式写出来就是Berry联络  ,其是由靶空间诱导出来。几何相位起源于靶空间的拓扑非平庸性——
,其是由靶空间诱导出来。几何相位起源于靶空间的拓扑非平庸性——  南北极是球面上的奇点。这就是造成
南北极是球面上的奇点。这就是造成 流形区别于拓扑平庸的平面流形的原因:这两种流形之间不存在同胚映射(即不可能把球的南北极都画在一张纸上)。
流形区别于拓扑平庸的平面流形的原因:这两种流形之间不存在同胚映射(即不可能把球的南北极都画在一张纸上)。

在平面中,闭合路径 意味着
意味着 转
转 角度,Berry相位为
角度,Berry相位为 ;而上面的几何角度来看,Berry曲率就是靶空间的边界曲面的曲率,由靶空间中单位面积的立体角度给出,也就是角度微元一半(由几何定义不难得出角度微元等于面积微元
;而上面的几何角度来看,Berry曲率就是靶空间的边界曲面的曲率,由靶空间中单位面积的立体角度给出,也就是角度微元一半(由几何定义不难得出角度微元等于面积微元  ) 在方向
) 在方向 上投影
上投影

在动量空间中Berry曲率在整个二维闭合Brillouin区 上积分,得到的结果相当于
上积分,得到的结果相当于  包围着靶空间中闭合Bloch面转过的圈数(缠绕数)
包围着靶空间中闭合Bloch面转过的圈数(缠绕数) 倍,其值完全取决于参数空间的拓扑性质,这也就是第一陈类:
倍,其值完全取决于参数空间的拓扑性质,这也就是第一陈类:
通过陈数也就给出Hall电导量子化的结果,这种机制是Dirac磁单极子量子化。
石墨烯一个Brillouin区有两个Dirac点 ,电子在石墨烯低能输运时就考察这两点的情况。在无磁场时,哈密顿量无质量项,这时,这两点特征值
,电子在石墨烯低能输运时就考察这两点的情况。在无磁场时,哈密顿量无质量项,这时,这两点特征值  ,
,  为零。在加了磁场后,破坏时间反演对称,Dirac点打开能隙
为零。在加了磁场后,破坏时间反演对称,Dirac点打开能隙 ;
; 产生了质量项
产生了质量项 ,
, 依据它们正负号
依据它们正负号 遍历Bloch球面的南北极。假设这个磁场是和晶格具有一样的周期性正负号变化,从而使得时间反演对称性破坏,而总平均磁场为零,而
遍历Bloch球面的南北极。假设这个磁场是和晶格具有一样的周期性正负号变化,从而使得时间反演对称性破坏,而总平均磁场为零,而 位于Brillouin区两顶点上,因此
位于Brillouin区两顶点上,因此 ,由结构反演对称性,
,由结构反演对称性, ;这时纵向电导符号相反
;这时纵向电导符号相反  ,石墨烯有能隙无边缘态,那么电导合贡献为零,整个体系处于绝缘体相。处于量子Hall相时,磁场方向大小恒定,每个Dirac点上有一条手征边缘态,贡献的Hall电导加起来得到
,石墨烯有能隙无边缘态,那么电导合贡献为零,整个体系处于绝缘体相。处于量子Hall相时,磁场方向大小恒定,每个Dirac点上有一条手征边缘态,贡献的Hall电导加起来得到  ,这就产生整数量子化Hall电导。
,这就产生整数量子化Hall电导。
石墨烯是由碳原子排列成六边形结构而形成,可以看作每个晶胞中有一个以两个原子为基础的三角结构。晶格向量可以写成

*石墨烯晶体简化结构,石墨烯一个原胞中包含两个不等价的碳原子

石墨烯特别重要的物理性质是
实空间中三个最邻近矢量
六个次邻近点距离矢量为
对石墨烯的周期六角格点系统采用电子紧束缚模型,只考虑到最近邻原子之间的相互作用,电子可以跳到的最邻近原子。在二次量子化的哈密顿量,有如下形式
这里我们以最低准粒子激发能量
Nambu表象下可写出BdG矩阵:
在晶格A 上
则动量表象中哈密顿量为
由此可以算出色散关系为:

加号对应较高频能谱 (
其中
同理,假如要考虑次近邻原子的相互作用,定义以
我们发现次近邻原子的引入,破坏了能带结构的对称,此时导带和价带不再对称,主要是因为次近邻原子的引入相当于引入了晶格格点轨道能级,因此近邻格点的引入使得Dirac点发生移动。

从色散关系我们能够看到次近邻原子的引入改变了Dirac点位置,破坏了电子空穴对称。另外我们发现,能量简并度与动量在动量空间的夹角有关(注意,展开直到
其中

其中
简明起见,我们先根据之前在动量表象下的哈密顿量来推导,在
去除一个无关紧要的相位因子
在紧束缚时,有效哈密顿量为:
二维Pauli矩阵向量
有效哈密顿量由两个无质量Dirac粒子(一个在
二分量旋量电子波函数在
在动量空间中,
我们把坐标原点定在
现在对于
由紧束缚近似方法可将单层石墨烯推广到多层石墨烯系统,乃至叠堆成三维石墨结构。最简单的是双层石墨烯结构,这种结构可以在导带和价带间打开一个能隙。

紧束缚近似哈密顿量写为
在扩大Brillouin区中考察动量接近
其中
求解可得到对称能谱图

若
哈密顿量中
,能谱是电子-空穴对称的。有两个额外的能带在
所引起的色散关系如前面的能谱图,和打开的能隙接近,但是并不直接在
将
1.石墨烯中的整数量子Hall效应
人们最开始着研究的量子Hall效应有效能带理论,是从石墨烯晶格开始。对于IQHE,Haldane于1988年发表的PRL中构造的模型是石墨烯晶格加上均匀磁场。石墨烯是个二维晶格,经过上面的介绍,我们知道了石墨烯能带是Dirac锥,可以产生无能隙激发——无质量Dirac费米子。在低能有效理论中,哈密顿量是Dirac形的,解出两条能带:价带和导带,它在Dirac点接触,能谱是线性的。我们在这里对Dirac哈密顿量用另一种形式重新表述——Bloch矢量;因为我们知道对于二能级系统,其Bloch矢可以画出一个Bloch球面(类比于自旋系统,这种矢量可以称为“赝自旋”)。这里Dirac点附近二能带模型的Bloch也可以类似地用这种办法写出来:
其中Pauli矩阵

哈密顿量为
有效质量项使得能谱打开能隙:
这时候无限大晶格系统从导体变成绝缘体,这是参数引起的相变。当进一步考虑有限晶格系统时候,我们会计算得到边缘态(表面态)。为此我们考察半无限晶格系统,在
从Dirac方程可以得到波函数旋量解:

而且此边缘态具有手征性,这一点可以计算其沿着边界上的群速度

根据TKNN四人的工作,量子Hall电导可以通过计算第一陈类得到,拓扑能带理论的核心在于Brillouin区上的Berry相位。Bloch态在规范变换下不变
我们需要对动量空间的几何性质进行考察 ,二维方形晶格

Berry相位就是Berry联络在动量空间
那么Berry曲率为
周期性晶格势场中Bloch态在一个倒格矢周期上最多只差一个相因子,因此边界关系为:

石墨烯Brillouin区是六边形,或以倒格子原胞看是菱形四边形,情况类似。


联络分量为
Berry相位为
由Brillouin区边界上波函数的相位关系:
可最终得到:
由波函数的单值性,则相位差取值只能是
此即Berry相位取值,这就解释了能带填满时候Hall电导出现整数量子化现象。在无磁场时候没有Hall效应,相因子相同,故

前面提过由于Bloch态具有
在有磁场时形成的量子Hall相之后,多出了一条无能隙边缘态连接导带和价带使得Brillouin流形重构。

这时候Brillouin区的几何流形是Möbius带,陈数就从原来普通环面的零变成了一 ,这也就是量子Hall电导的填充数。

用陈类对量子Hall态分类的思想对应于数学上用Euler示性类对二维紧致定向流形分类:Berry曲率对应于Gauss曲率,第一陈类对应于Euler示性类,那么
这里
现在我们用另一个角度描述Berry相位。我们记得这节开头之所以用Bloch矢量

在平面中,闭合路径
在动量空间中Berry曲率在整个二维闭合Brillouin区
通过陈数也就给出Hall电导量子化的结果,这种机制是Dirac磁单极子量子化。
石墨烯一个Brillouin区有两个Dirac点
本文由Phantom_Ghost授权(果壳网)发表,文章著作权为原作者所有。
2条评论
你的评论
X
qed: still 可交换 abelian group, vs. non 可交换abelian group gauge field theory
诱导度规是轨迹的函数 non-非线性的问题,它对轨迹有没有动力学反馈; 整个度规求导是Killing motion, 与轨迹切向正交的子空间上的诱导度 ...
张永德教授量子力学讲义 第十一章
.3 几种常见含时微扰的一阶近似计算 1, 常微扰
假定微扰H与时间无关,并且按体系特征时间
mn
1
ω尺度衡量,H是在足够长时间TT
-,22
内加在系统上。这时,按上面一阶近似
[PDF]introduction to the path integral - Clarkson University
people.clarkson.edu/~lschulma/1988TriestePathIntegralLectures.pdf
by LS Schulman - Cited by 6 - Related articles
An overview of the major trends in the use of the path integral. ..... The important paths that contribute to Brownian motion—as in the Wiener integral, Eq ..... In any case, I would not be the least dissatisfied if by using the path integral formulation.
Kac who recognized around 1950 that Feynman's path integral was an
analytic continuation of sorts of the Wiener functional integral used in Brownian motion.
1. Measure theory, Wiener integral, etc.
2. Pseudomeasures and other approaches to the complex \measure"
3. Large Deviation techniques
analytic continuation of sorts of the Wiener functional integral used in Brownian motion.
2. Pseudomeasures and other approaches to the complex \measure"
3. Large Deviation techniques
math01 费曼路径积分Wiener process - 热点讨论主题 - 文学城
bbs.wenxuecity.com › 论坛 › 音乐快递
轉為繁體網頁
2011年11月16日 - math01 费曼路径积分Wiener process ... episte.math.ntu.edu.tw/articles/mc/
bbs.wenxuecity.com › 论坛 › 音乐快递
轉為繁體網頁
2011年11月16日 - math01 费曼路径积分Wiener process ... episte.math.ntu.edu.tw/articles/mc/轉為繁體網頁
tw01 levy01 Brown01 運動與Lévy 泛函分析(下) - 费曼路径 ...
phymath999.blogspot.com/.../tw01-levy01-brown01-levy-... - 轉為繁體網頁
2014年1月17日 - www.math.sinica.edu.tw/math_media/d172/17207.pdf. 對於此種無限維分析學 ... math01 费曼路径积分Wiener process - 热点讨论主题- 文学城.
phymath999.blogspot.com/.../tw01-levy01-brown01-levy-... - 轉為繁體網頁
2014年1月17日 - www.math.sinica.edu.tw/math_media/d172/17207.pdf. 對於此種無限維分析學 ... math01 费曼路径积分Wiener process - 热点讨论主题- 文学城.非平衡统计动力学Ito积分. 数值积分. 是Wiener过程增量
phymath999.blogspot.com/2013/12/ito-wiener.html
轉為繁體網頁
2013年12月18日 - staff.ustc.edu.cn/~hzhlj/. ... phymath999: 【股價變動過程及Ito 定理】 Wiener Process的樣本路徑是. ... 的规范理论 · read01 路径积分积分变量—路径—本身是时空的函数,所以它是推广了的黎曼积分,即所谓的泛函积分. ... 这才是规范理论的初衷 · 费曼路径积分为什么在数学上不严格 · 铂金的主要用途是汽车的尾气 ...
phymath999.blogspot.com/2013/12/ito-wiener.html
轉為繁體網頁
2013年12月18日 - staff.ustc.edu.cn/~hzhlj/. ... phymath999: 【股價變動過程及Ito 定理】 Wiener Process的樣本路徑是. ... 的规范理论 · read01 路径积分积分变量—路径—本身是时空的函数,所以它是推广了的黎曼积分,即所谓的泛函积分. ... 这才是规范理论的初衷 · 费曼路径积分为什么在数学上不严格 · 铂金的主要用途是汽车的尾气 ...轉為繁體網頁
維納過程- 維基百科,自由的百科全書 - Wikipedia
zh.wikipedia.org/zh-hk/维纳过程
數學中,維納過程(英語:Wiener process)是一種連續時間隨機過程,得名於諾伯特·
缺少字詞: cedu
zh.wikipedia.org/zh-hk/维纳过程
數學中,維納過程(英語:Wiener process)是一種連續時間隨機過程,得名於諾伯特·
缺少字詞: cedu
读书笔记- 人人小站
zhan.renren.com/takingnotes?page=7&from=pages
轉為繁體網頁
2012年1月2日 - http://www.phy.duke.edu/~rgb/Class/phy319/phy319/node72.html. # green函数. 2011 / . 年12 / ... 总结一下就是我觉得费曼的路径积分其实有两个tricky的地方. 1.
zhan.renren.com/takingnotes?page=7&from=pages
轉為繁體網頁
2012年1月2日 - http://www.phy.duke.edu/~rgb/Class/phy319/phy319/node72.html. # green函数. 2011 / . 年12 / ... 总结一下就是我觉得费曼的路径积分其实有两个tricky的地方. 1.轉為繁體網頁
科学网—我的诸多烂尾工程...之一- 王雄的博文 - 科学网—博客
blog.sciencenet.cn/blog-439941-695934.html
轉為繁體網頁
2013年6月2日 - https://web.math.princeton.edu/~nelson/papers/talk.pdf. The mystery of stochastic .... 3 进而和费曼路径积分的关系。。。 4 最终打通从薛定谔到波 ...
blog.sciencenet.cn/blog-439941-695934.html
轉為繁體網頁
2013年6月2日 - https://web.math.princeton.edu/~nelson/papers/talk.pdf. The mystery of stochastic .... 3 进而和费曼路径积分的关系。。。 4 最终打通从薛定谔到波 ...轉為繁體網頁
Search history function requires JavaScript. - Library of ...
las.sinica.edu.tw/search*chi/i?SEARCH=9789576938191
量子力學與路徑積分/ [美]R. P. 費曼, A.R.希布斯著; 張邦固,韋秀譯希布斯, A. R.(
las.sinica.edu.tw/search*chi/i?SEARCH=9789576938191
量子力學與路徑積分/ [美]R. P. 費曼, A.R.希布斯著; 張邦固,韋秀譯希布斯, A. R.([DOC]《Field Theory:A Modern Primer》评介 - 南开大学
www2.lib.nankai.edu.cn/.../《Field%20Theory:A%20Mo...
轉為繁體網頁
Lubos Motl评价本书时说到,读者可以从书中学到用费曼图计算格林函数和散射振幅的方法。标量Klein-Gordon场在最开始被用作一个教学事例,路径积分的思想贯穿 ...
缺少字詞: wiener
www2.lib.nankai.edu.cn/.../《Field%20Theory:A%20Mo...
轉為繁體網頁
Lubos Motl评价本书时说到,读者可以从书中学到用费曼图计算格林函数和散射振幅的方法。标量Klein-Gordon场在最开始被用作一个教学事例,路径积分的思想贯穿 ...轉為繁體網頁
缺少字詞: wiener
Table I. Some Trends in Path Integration
I. Asymptotics
1. Semiclassical (~!0) methods, chaos, chemical applications
2. Short wavelength approximation, Geometrical Theory of Di®raction
3. Instantons
4. Other large parameter situations including mean ¯eld theory
(Range !1) and weak coupling approximations
II. Getting rid of an in¯nite number of degrees of freedom
1. QED (photons)
2. Polarons (phonons)
3. Dissipation and quantum tunneling (phonons)
4. And on and on and on
III. Inserting an in¯nite number of degrees of freedom
1. Uncompleting the square, Ising model as functional integral
2. Random potential distribution function
IV. Renormalization and scaling
1. Partition function as functional integral
V. Variational principles
VI. Field theory
1. Analytic continuation, Euclidean quantum ¯eld theory
2. Bosons, Fermions and supersymmetry
VII. Polymers
VIII. Machine summation
1. Statistical mechanics, long time asymptotics
2. QCD
IX. Topological considerations and curved space
1. Homotopy
2. Curvature, constrained systems
3. Relativity, spin
4. Operator ordering
X. Grassmann variables
1. Fermions
2. Combinatorial applications
XI. Exact Solutions
XII. Mathematical
1. Measure theory, Wiener integral, etc.
2. Pseudomeasures and other approaches
为什么路径积分中只是研究连续的路径
在做路径积分的时候,总是默认我们选出的是一条连续的路径。我上次听过一次这种说法:“从无限条路径中取出一条连续的路径跟从实数轴上取出一个有理数的概率一样,都是零,为什么不去研究处处不连续的路径呢?所以我只能认为这是一个假设。”当时是在开组会,貌似大家也没有什么反对意见。
可是今天我看sakurai的时候觉得不是这样的,有一个东西保证了我们取路径的时候总是能取到一条连续的路径。

于是路径积分中的<xj tj|xi ti>就同propagator联系起来了,而propagator有两个很简单的性质

这里关心第二个性质就行了,注意这是个取极限的过程,所以保证了K是连续的。而回到路径积分,这就说明我们取出的路径是连续的。
说的更直白一点,我们有
(2.5.43是Heisenberg picture下,同一时刻的时候,位置基矢必须正交的要求)如果tn趋向tn-1时,xn不等于xn-1,那么这条路径对应的积分就是零。
总结一下就是我觉得费曼的路径积分其实有两个tricky的地方
1.通过delta函数保证我们取出连续的路径
2.通过
这个条件保证我们取出真实的“路径”。
可是今天我看sakurai的时候觉得不是这样的,有一个东西保证了我们取路径的时候总是能取到一条连续的路径。

于是路径积分中的<xj tj|xi ti>就同propagator联系起来了,而propagator有两个很简单的性质

这里关心第二个性质就行了,注意这是个取极限的过程,所以保证了K是连续的。而回到路径积分,这就说明我们取出的路径是连续的。
说的更直白一点,我们有

(2.5.43是Heisenberg picture下,同一时刻的时候,位置基矢必须正交的要求)如果tn趋向tn-1时,xn不等于xn-1,那么这条路径对应的积分就是零。
总结一下就是我觉得费曼的路径积分其实有两个tricky的地方
1.通过delta函数保证我们取出连续的路径
2.通过

这个条件保证我们取出真实的“路径”。
"物理"对应"数学"名词词典 zz from 繁星客栈 作者 季候风
季候风:
有时候物理理论和数学理论研究类似的对象, 但是由于各自独立的发展, 所使用的术语有很大的差别; 有时候物理学家先发展了一些理论, 数学家从中找到一些有趣的结构加以进一步研究; 有时候物理学家发现他们的理论可以用来解释一些神秘的数学现象和令人困惑的数学理论......以下这个 "词典" 就试图部分总结一下以上提到的这几种 "物理/数学 对偶", 抛砖引玉, 欢迎补充.
经典力学 <----> 辛几何
位形空间 / 微分流形
相空间 / 余切丛
Hamilton 正则方程 / 辛梯度场
运动方程的解 / Hamilton 流动
正则变换 / 辛同胚, Lagrange 子流形
Hamilton-Jacobi 方法 / 等值面极化
狭义相对论 <----> 群表示论
标量 / SO(3,1) 的平凡表示空间中的元素
矢量 / SO(3,1) 的定义表示空间中的元素
张量 / SO(3,1) 的定义表示空间及其对偶的张量积中的元素
旋量 / SL(2,C) 的二维不可约表示空间及其对偶的张量积中的元素
量子论 <----> 泛函分析
右矢 / Hilbert 空间的元素
左矢 / 对偶空间的元素
算符 / 算子
共轭算符 / 伴随算子
算符作用于左矢 / 对偶算子
Hermite 算符 / 自伴算子
本征值 / 谱点
离散本征值 / 点谱
连续本征值 / 连续谱
算子微积 / Gelfand 表示
delta 函数 / delta 泛函
位移算符 / 空间平移群的酉表示的无穷小生成元
时间演化 / 酉算子群
Schrodinger 方程 / Stone 定理
表象 / Hilbert 空间的形式及正交基的选取
表象变换 / Hilbert 空间同构
Schrodinger 表象 / Stone-von Neumann 定理
路径积分 / Wiener 测度
规范场论 <----> 纤维丛的几何
场 / 丛的截面
整体对称性(规范群) / 纤维空间的自同构群
规范对称性 / 丛的自同构群
规范势 / 主丛上的联络
规范力 / 联络的曲率
规范荷 / 规范群的表示
带荷的物质场 / 规范群表示从主丛诱导的向量丛的截面
协变导数 / 主丛上的联络诱导的向量丛上的联络
规范 / 局部平凡化
规范不变的 / 丛上整体定义的, 或者在丛的自同构下不变的
Maxwell 方程组 / Hodge 理论
弦论 <----> 拓扑学? 几何学? 新拓扑学? 新数学?
非线性 sigma 模型 / Morse理论, Floer理论, Gromov-Witten 理论
拓扑弦 / 低维流形不变量 ( Khovanov-Rozansky, Jones-Witten, ...), Langlands 猜想(?)
B-场 / 扭曲 K-理论
共形场论 / 魔群, 月光模
拓扑共形场论 / 弦拓扑(?)
???
量子场论 <----> 低维拓扑
Abel群 Chern-Simons 场论 / 链接数, 挠数
超对称量子场论 / Donaldson 不变量
紧群 Chern-Simons 场论 / Jones-Drinfeld 不变量
微扰 Chern-Simons 场论 / Vassiliev 不变量
3维引力 / 双曲几何
Liouville 共形场论 / Teichmuller 理论
N=2 超对称量子场论 / Seiberg-Witten 不变量
N=4 超对称量子场论 / 几何 Langlands 计划
有时候物理理论和数学理论研究类似的对象, 但是由于各自独立的发展, 所使用的术语有很大的差别; 有时候物理学家先发展了一些理论, 数学家从中找到一些有趣的结构加以进一步研究; 有时候物理学家发现他们的理论可以用来解释一些神秘的数学现象和令人困惑的数学理论......以下这个 "词典" 就试图部分总结一下以上提到的这几种 "物理/数学 对偶", 抛砖引玉, 欢迎补充.
经典力学 <----> 辛几何
位形空间 / 微分流形
相空间 / 余切丛
Hamilton 正则方程 / 辛梯度场
运动方程的解 / Hamilton 流动
正则变换 / 辛同胚, Lagrange 子流形
Hamilton-Jacobi 方法 / 等值面极化
狭义相对论 <----> 群表示论
标量 / SO(3,1) 的平凡表示空间中的元素
矢量 / SO(3,1) 的定义表示空间中的元素
张量 / SO(3,1) 的定义表示空间及其对偶的张量积中的元素
旋量 / SL(2,C) 的二维不可约表示空间及其对偶的张量积中的元素
量子论 <----> 泛函分析
右矢 / Hilbert 空间的元素
左矢 / 对偶空间的元素
算符 / 算子
共轭算符 / 伴随算子
算符作用于左矢 / 对偶算子
Hermite 算符 / 自伴算子
本征值 / 谱点
离散本征值 / 点谱
连续本征值 / 连续谱
算子微积 / Gelfand 表示
delta 函数 / delta 泛函
位移算符 / 空间平移群的酉表示的无穷小生成元
时间演化 / 酉算子群
Schrodinger 方程 / Stone 定理
表象 / Hilbert 空间的形式及正交基的选取
表象变换 / Hilbert 空间同构
Schrodinger 表象 / Stone-von Neumann 定理
路径积分 / Wiener 测度
规范场论 <----> 纤维丛的几何
场 / 丛的截面
整体对称性(规范群) / 纤维空间的自同构群
规范对称性 / 丛的自同构群
规范势 / 主丛上的联络
规范力 / 联络的曲率
规范荷 / 规范群的表示
带荷的物质场 / 规范群表示从主丛诱导的向量丛的截面
协变导数 / 主丛上的联络诱导的向量丛上的联络
规范 / 局部平凡化
规范不变的 / 丛上整体定义的, 或者在丛的自同构下不变的
Maxwell 方程组 / Hodge 理论
弦论 <----> 拓扑学? 几何学? 新拓扑学? 新数学?
非线性 sigma 模型 / Morse理论, Floer理论, Gromov-Witten 理论
拓扑弦 / 低维流形不变量 ( Khovanov-Rozansky, Jones-Witten, ...), Langlands 猜想(?)
B-场 / 扭曲 K-理论
共形场论 / 魔群, 月光模
拓扑共形场论 / 弦拓扑(?)
???
量子场论 <----> 低维拓扑
Abel群 Chern-Simons 场论 / 链接数, 挠数
超对称量子场论 / Donaldson 不变量
紧群 Chern-Simons 场论 / Jones-Drinfeld 不变量
微扰 Chern-Simons 场论 / Vassiliev 不变量
3维引力 / 双曲几何
Liouville 共形场论 / Teichmuller 理论
N=2 超对称量子场论 / Seiberg-Witten 不变量
N=4 超对称量子场论 / 几何 Langlands 计划
在迈向成功的道路上,爱因斯坦获得飞跃性的认识来源于对刚体转动圆盘的研究。在他1912年2月所发表的《光速和引力场的静力学》一文中,他认为,由于洛仑兹收缩,圆周与半径之比不再为π,这表明,惯性系的观察者得出沿圆周运动方向运动的尺有尺缩效应,而相对非惯性旋转系的观察者根据等效原理,会认为所在系是静止不动的,却存在着一个“离心的引力场”,由于圆周与半径之比不再为π,他自然会解释为,由于这一引力的存在,使欧几里德几何不再成立。将这一结论扩展到一切真实引力场,有引力的空间都将不再是欧几里德的。这就是爱因斯坦所解释的,“把等效原理和狭义相对论结合起来,很自然地得出,引力与非欧几何联系在一起”的结论。当时爱因斯坦对非欧几何所知甚少,仅在大学读书时从基塞(Geiser)教授那里学到一点微分几何的知识,正是其中有关高斯曲面理论使爱因斯坦受到启发。他曾回忆道,“直到1912年,当我偶然想到高斯的曲面理论可能就是解开这个奥秘的关键时,这个问题才获得了解释。我发现,高斯曲面坐标对于理解这个问题是十分有意义的。”①
德国数学家高斯(Gauss, Johann Karl Freidrich1777~1855)从大地测量中受到启发,创立了二维曲面的微分几何理论。他在曲面上引入曲线坐标u和v,并证明曲面上任意线元具有如下普遍形式
ds2=g11du2+g12dudv+g21dvdu+g22dv2
其中g11,g12,g21,g22均为变量u和v的函数,称之为度规,它们由曲面的物质所决定。根据高斯的曲线坐标和度规,不仅可以确定曲面上的测地线(即弯曲空间的“直线”),还可以找到曲面的曲率,并进一步证明曲面所在空间的非欧几里德性质。高斯曲面即为一种弯曲的二维空间结构,然而在其中一点的任意一个小的邻域上,它应近似为平面,在这个局域,欧氏几何仍将成立,并与局域的笛卡尔系相对应。
爱因斯坦把引力空间与高斯曲面理论做了类比思考,他发现,引力所在的空间具有类似高斯曲面的几何性质,特别是当他把闵可夫斯基对狭义相对论所做的解释与引力问题联系起来以后,就更认识到其中的重要含意,这些观念成为了广义相对论理论形成的重要因素。他曾说“没有这个观念,广义相对论恐怕无法成长”,因为闵可夫斯基的四维世界“与高斯曲面理论相结合,向人们展示,存在引力场时,空间是弯曲的,欧氏几何不再成立,这表面引力场中不存在全局性的或大范围的惯性系,但对每一时空点附近的一个小的局域而言,却是闵可夫斯基平直的,欧氏几何仍成立,同时也存在与之对应的‘局域惯性系’。”这实际就是“爱因斯坦升降机”的思想。爱因斯坦明确地指出,“高斯的曲面理论与广义相对论间最重要的接触点就在于度规的性质,这些性质是建立两种理论概念的重要基础。”在1912年3月,爱因斯坦在《静引力场理论》中又指出,“等效原理只能在局域中成立”,这一系列思想表明,爱因斯坦看到了引力与时空几何结构间的联系,这就是引力场影响着时空结构,乃至决定着它的度规的规律。
高级微观经济学 - 第 32 頁 - Google 圖書結果
https://books.google.com.hk/books?isbn=7302041717 - 轉為繁體網頁
武康平 - 2001 - Microeconomics
二、价格的表示(一)价格向量我们首先考虑有限维经济中商品价格的表示问题。设商品空间为 R ' ,用九表示一个单位商品 i 所能交换的货币量,则角就是商品 i 的价格( i
"在此之前,我们不妨先看一下时空、引力和物质之间的关系,我这里说保守的说法:时空有其固有的几何结构,就是我们常说的Lorentz群结构,如果不考虑物质的影响,我们可以称之为纯度规场;引力有来源,是物质的能量动量张量,引力的来源的张量要求其实已经表达了这样一个意思,就是物质场和纯度规场的耦合,或者换句话说,我们写出的表述物质的Lagrangian被要求是广义协变的。在爱因斯坦引力理论里面,时空、引力和物质就是这样的一种联系,物质就是物质,时空就是时空,相比粒子物理的规范相互作用,引力理论中所谓的规范相互作用(物质场和纯度规场的所谓耦合),很不相同,从这个角度看,我本人认为,引力理论不存在被要求实现量子化的条件。所以,跳出这个话题,如果你问暗物质是否会影响时空几何结构?那么答案应该是明显的,时空的几何结构不会被物质所影响,只不过能够表现出来物质的引力效应"
2014年12月12日 - sr01 gr01 诱导度规是轨迹的函数非线性的问题,它对轨迹有没有动力学反馈; 整个度规求导是Killing motion, 与轨迹切向正交的子空间上的诱导度 ...
荊陽青龍公 (公丘子) 2012-05-03 11:23:37
可能是因爲度槼是決定時空性質的唯一物理量,所以,應該對度槼求變分。再者,愛因斯坦方程就是關於度槼的二階方程。
我遇到過這種情況。給出電磁場張量和對應的拉氏量,用變分法求出麥克斯韋方程組。如果對協變的四矢求變分,非常好算且能得到麥克斯韋方程。但是,若是對逆變四矢求變分,非常複雜;我沒認真算,但是,我估計得不到麥克斯韋方程。
正確的是:麥克斯韋方程組是一樣的,能動量張量可能不一樣。繼續驗証中
那么假设度规不是基本场,不能表达所有的引力的性质,我们就可以得到对广相的修正,选择合适的度 那么假设度规不是基本场,不能表达所有的引力的性质,我们就可以得到对广相的修正,选择合适的度规函数,可以跟观测对比,取得合理的形式。
在引力理论里面,把作用量看做度规的协变还是逆变形式的泛函,对于正统的 GR 来说没有区别
https://books.google.com.hk/books?isbn=7302041717 - 轉為繁體網頁
武康平 - 2001 - Microeconomics
二、价格的表示(一)价格向量我们首先考虑有限维经济中商品价格的表示问题。设商品空间为 R ' ,用九表示一个单位商品 i 所能交换的货币量,则角就是商品 i 的价格( i求问,有关微分几何_相对论吧_百度贴吧
tieba.baidu.com/p/2453906058 - 轉為繁體網頁
至于联络是为了在微分流形上对矢量场求导而出现的,它先验地跟度规并没有关系。 ... 而我们往往只对跟度规相契合的那个联络感兴趣(因为我们希望导数为0有几何 ...
tieba.baidu.com/p/2453906058 - 轉為繁體網頁
度规的意义_百度文库
wenku.baidu.com/view/528ffc1da300a6c30c229fec.html
轉為繁體網頁
2011年3月24日 - 关键词:度规;度规积分;度规导数;变度规实数轴;度规度量中图分类 ... 公式(1)是已知度规求向量的问题,我们称作常度规实数轴的积分问题。
"度規求导数"
轉為繁體網頁
愛因斯坦-希爾伯特作用量- 維基百科,自由的百科全書
zh.wikipedia.org/zh-hk/爱因斯坦-希尔伯特作用量
在廣義相對論中,作用量一般都被認為是度規(以及物質場)的一個泛函,而其聯絡是 ... 在第二行中我們使用了上面得到的里奇張量的變分結果以及協變導數對度規的 ...
zh.wikipedia.org/zh-hk/爱因斯坦-希尔伯特作用量
[PDF]第五章引力场方程
astronomy.nju.edu.cn/~tyhuang/jiaoxue/chapter5.pdf
轉為繁體網頁
偏导数的线性组合,可以猜测度规gµν 相当于牛顿力学中的引力势. 广义相对论的 ..... 边对度规求变分时,非齐次项不复存在,说明克氏符号的变分是张量. 这样,只需将 ...
astronomy.nju.edu.cn/~tyhuang/jiaoxue/chapter5.pdf
轉為繁體網頁
轉為繁體網頁
sr01 gr01 诱导度规是轨迹的函数非线性的问题,它对轨迹有 ...
phymath999.blogspot.com/.../sr01-gr01-killing-motion.ht...
轉為繁體網頁
2014年12月12日 - sr01 gr01 诱导度规是轨迹的函数非线性的问题,它对轨迹有没有动力学反馈; 整个度规求导是Killing motion, 与轨迹切向正交的子空间上的诱导度 ...
phymath999.blogspot.com/.../sr01-gr01-killing-motion.ht...
轉為繁體網頁
轉為繁體網頁
求问,有关微分几何_相对论吧_百度贴吧
tieba.baidu.com/p/2453906058 - 轉為繁體網頁
至于联络是为了在微分流形上对矢量场求导而出现的,它先验地跟度规并没有关系。 ... 而我们往往只对跟度规相契合的那个联络感兴趣(因为我们希望导数为0有几何 ...
tieba.baidu.com/p/2453906058 - 轉為繁體網頁
度规的意义_百度文库
wenku.baidu.com/view/528ffc1da300a6c30c229fec.html
轉為繁體網頁
2011年3月24日 - 关键词:度规;度规积分;度规导数;变度规实数轴;度规度量中图分类 ... 公式(1)是已知度规求向量的问题,我们称作常度规实数轴的积分问题。
wenku.baidu.com/view/528ffc1da300a6c30c229fec.html
轉為繁體網頁
轉為繁體網頁
科学网—大理石和木头- 王雄的博文 - 科学网—博客
blog.sciencenet.cn/blog-439941-716575.html
轉為繁體網頁
2013年8月13日 - 作用量原理告诉我们这个作用量对度规 g^{.mu.nu}., ... 由于这个方程要求对所有变分 .delta g^{.mu.nu} ... 根据对行列式进行求导的雅可比公式.
blog.sciencenet.cn/blog-439941-716575.html
轉為繁體網頁
轉為繁體網頁
[DOC]度规的意义 - 教育数学会
www.emath.cn/ytdg.doc
轉為繁體網頁
公式(1)是已知度规求向量的问题,我们称作常度规实数轴的积分问题。 .... 时,由公式(3)和公式(3′)可知=,度规导数与导数等价,以后可以把度规导数称作导数。
www.emath.cn/ytdg.doc
轉為繁體網頁
轉為繁體網頁
【揭秘】从爱因斯坦场方程说起/ databit / 第6页-[天涯] - 贴库网
www.tieku001.com › 天涯 › 煮酒论史
轉為繁體網頁
对坐标求导能求出质量量纲来?我确实是没常识,不但没常识,恐怕连理解这个观点的智商都没有,所以我请教下对度规的二次求导怎么变出质量量纲的,望不吝赐教。
www.tieku001.com › 天涯 › 煮酒论史
轉為繁體網頁
轉為繁體網頁
对谁做变分[误] - 豆瓣
www.douban.com/group/topic/29311922/
轉為繁體網頁
2012年5月1日 - ... 矢量场,t 是个张量场,metric 是度规, 省略号表示这些量的高阶导数项。 ... 如果对
www.douban.com/group/topic/29311922/
轉為繁體網頁
轉為繁體網頁
豆瓣小组
对谁做变分[误]
来自: 编程的章鱼喵(=L=~=M=) 2012-05-01 13:08:30
这种问法是不对的。正确的问法应该是,作用量看作不同函数的泛函的时候,如何如何。只要知道了正确的问法,答案就立刻出来了。
----------------------------------------------
一个作用量 S[phi, u, t, metric, ...],其中 phi 是个标量场,u 是个矢量场,t 是个张量场,metric 是度规, 省略号表示这些量的高阶导数项。
在变分原理里面,如果想对一个作用量做变分,求极值。那么到底该对哪个量做变分呢?
GR 里面一般是对 metric 变分的,QFT 里面一般是对基本场做变分的,那么如果是这么复杂的作用量,应该对谁做变分呢?
对不同的量做变分不太等价,GR 里面有个 Palatini 形式,是对联络做变分的,大部分情况下跟 GR 的度规变分形式等价,有些情况下就不等价了。
这种问法是不对的。正确的问法应该是,作用量看作不同函数的泛函的时候,如何如何。只要知道了正确的问法,答案就立刻出来了。
----------------------------------------------
一个作用量 S[phi, u, t, metric, ...],其中 phi 是个标量场,u 是个矢量场,t 是个张量场,metric 是度规, 省略号表示这些量的高阶导数项。
在变分原理里面,如果想对一个作用量做变分,求极值。那么到底该对哪个量做变分呢?
GR 里面一般是对 metric 变分的,QFT 里面一般是对基本场做变分的,那么如果是这么复杂的作用量,应该对谁做变分呢?
对不同的量做变分不太等价,GR 里面有个 Palatini 形式,是对联络做变分的,大部分情况下跟 GR 的度规变分形式等价,有些情况下就不等价了。
----------------------------------------------
一个作用量 S[phi, u, t, metric, ...],其中 phi 是个标量场,u 是个矢量场,t 是个张量场,metric 是度规, 省略号表示这些量的高阶导数项。
在变分原理里面,如果想对一个作用量做变分,求极值。那么到底该对哪个量做变分呢?
GR 里面一般是对 metric 变分的,QFT 里面一般是对基本场做变分的,那么如果是这么复杂的作用量,应该对谁做变分呢?
对不同的量做变分不太等价,GR 里面有个 Palatini 形式,是对联络做变分的,大部分情况下跟 GR 的度规变分形式等价,有些情况下就不等价了。
广义相对论引起的科学思想革命
||
自爱因斯坦的论动体的电动力在1905年发表以来,在过去的近110年里,科学思想革命性变化的主线条是:
1. 四维空间(1维时间+三维空间)的偏导数运算【作为联系两点之间的客体变化量(单位长度上的函数变化量),忽略高价小量】,被升级为度规张量变换【作为联系两相邻线段之间的空间客体量】条件下的协变导数运算。而这种升级的客观物理基础就是:时空尺度的变化受到世界线长度客体不变性的制约。
从科学哲学上看,把四维空间的偏导数运算分为两类:一类是满足特定度规张量变换条件的,被看成是反映物理真实性的运算;其它的被划入第二类,不是物理真实的而是纯粹数学上的。这样就压缩了偏导数运算有效性的范畴。
出于这样的一个要点,物理量必须为张量就成为一条科学原理(协变性原理)。质点运动的概念被抛弃,而代之于运动轨迹概念。
2. 度规张量变换既然是客体(或运动),那么不同类别的客体(或运动)就有不同类别的度规张量变换(群变换),由此引出:度规张量变换(群变换)就是物质场(或物质运动),从而,用规范场论重新表达出的物理学就是用普通偏导数表达出的经典物理的升级版本。
引力场理论提供了一个典范,从而也开启了天体科学研究的新时代。由运动轨迹概念升级为流形演化概念。坐标概念被参考流形概念替代。
从科学哲学上看,数学上的流形映射就是物质运动的自然表达方式,从而,对流形映射的属性分类就是对物质运动属性的分类。从此,在科学思想上,摆脱了用直观表象进行物质运动属性分类的束缚,也因此而深入到了物质运动的更深层次。这是革命性的进步,从而也就在原则上能渗入任意学科。
3. 在近半个世纪以来,发现度规张量变换过于狭隘,无法把量子力学包括进来,在经历李代数这个中间环节后,在本世纪初,终于发现,把度规张量变换拓展为群变换后,再限定为超代数下的Clifford几何代数张量,也就可以把量子力学、色动力学也包含进来。而原来用的度规张量变换只是一个特例。
具体的超代数运算法则成为具体的物质抽象运动表述。
由此,又把物质运动的概念拓展为更大的类别,从而为处理复杂运动(复合性的物质运动)提供了理论工具。量子物理的新时代被开启了。
从科学哲学上看,它对流形映射概念加上了更多的限定(同时也扩充了映射的类别),复合属性成为物质运动复杂性的对应描述。原则上,可以完全的实现跨学科的高度抽象性的理论建构。
这就开启了现代物理的大门,也开启了物理学大小统吃的大门。一场科学革命的高潮期似乎是即将到来。
如果一个人无视这一百年来物理学家(作为整体)取得的物理学成就,那么他就只能生活在经典物理的世界里。
如果一个人还在度规张量变换水平上研究物理,发现广义相对论(物理学)的缺陷,他只不过是重复“1.”的线条,而且未必是正确的重复。
如果一个人还在群变换水平上研究物理,发现大量的原理是不足为奇的,他推翻这个原理也好,那个原理也好,总是可能的。但是,那是徒劳无功的。因为,他未必能给自身脱僵的思绪加上必要的束缚,就是加了,也未必加的正确。顶多是在“2.”圈内转来转去而已。
如果不能进入“3.”时代,无论如何叫喊,也是在现代物理的大门之外。
现实就是如此的不以人们的主观愿望而转移。
无论是批广义相对论也好,保广义相对论也好,作为现代物理学革命的导火线,也作为第一个成功的经典型范例,广义相对论作为最重要的环节的历史地位是任何理论和任何人所无法否定的
多个独立同分布随机变量序列经过适当的线性总和后,其分布仍然保持不变
尺度变换下具有不变性
[PDF]一、 引言 - 物理
www.wuli.ac.cn/fileup/PDF/19840501.pdf
轉為繁體網頁
由 KG Wilson 著作 - 1984
1984年5月1日 - 渐转到1971一1972年论述重整化群的文章.最 .... 重整化群近似就是依次积分掉涨落, 从原子标. 度的涨 ..... 一M彻) 应按波包函数的@) 的集合来进行.
自爱因斯坦的论动体的电动力在1905年发表以来,在过去的近110年里,科学思想革命性变化的主线条是:
1. 四维空间(1维时间+三维空间)的偏导数运算【作为联系两点之间的客体变化量(单位长度上的函数变化量),忽略高价小量】,被升级为度规张量变换【作为联系两相邻线段之间的空间客体量】条件下的协变导数运算。而这种升级的客观物理基础就是:时空尺度的变化受到世界线长度客体不变性的制约。
从科学哲学上看,把四维空间的偏导数运算分为两类:一类是满足特定度规张量变换条件的,被看成是反映物理真实性的运算;其它的被划入第二类,不是物理真实的而是纯粹数学上的。这样就压缩了偏导数运算有效性的范畴。
出于这样的一个要点,物理量必须为张量就成为一条科学原理(协变性原理)。质点运动的概念被抛弃,而代之于运动轨迹概念。
2. 度规张量变换既然是客体(或运动),那么不同类别的客体(或运动)就有不同类别的度规张量变换(群变换),由此引出:度规张量变换(群变换)就是物质场(或物质运动),从而,用规范场论重新表达出的物理学就是用普通偏导数表达出的经典物理的升级版本。
引力场理论提供了一个典范,从而也开启了天体科学研究的新时代。由运动轨迹概念升级为流形演化概念。坐标概念被参考流形概念替代。
从科学哲学上看,数学上的流形映射就是物质运动的自然表达方式,从而,对流形映射的属性分类就是对物质运动属性的分类。从此,在科学思想上,摆脱了用直观表象进行物质运动属性分类的束缚,也因此而深入到了物质运动的更深层次。这是革命性的进步,从而也就在原则上能渗入任意学科。
3. 在近半个世纪以来,发现度规张量变换过于狭隘,无法把量子力学包括进来,在经历李代数这个中间环节后,在本世纪初,终于发现,把度规张量变换拓展为群变换后,再限定为超代数下的Clifford几何代数张量,也就可以把量子力学、色动力学也包含进来。而原来用的度规张量变换只是一个特例。
具体的超代数运算法则成为具体的物质抽象运动表述。
由此,又把物质运动的概念拓展为更大的类别,从而为处理复杂运动(复合性的物质运动)提供了理论工具。量子物理的新时代被开启了。
从科学哲学上看,它对流形映射概念加上了更多的限定(同时也扩充了映射的类别),复合属性成为物质运动复杂性的对应描述。原则上,可以完全的实现跨学科的高度抽象性的理论建构。
这就开启了现代物理的大门,也开启了物理学大小统吃的大门。一场科学革命的高潮期似乎是即将到来。
如果一个人无视这一百年来物理学家(作为整体)取得的物理学成就,那么他就只能生活在经典物理的世界里。
如果一个人还在度规张量变换水平上研究物理,发现广义相对论(物理学)的缺陷,他只不过是重复“1.”的线条,而且未必是正确的重复。
如果一个人还在群变换水平上研究物理,发现大量的原理是不足为奇的,他推翻这个原理也好,那个原理也好,总是可能的。但是,那是徒劳无功的。因为,他未必能给自身脱僵的思绪加上必要的束缚,就是加了,也未必加的正确。顶多是在“2.”圈内转来转去而已。
如果不能进入“3.”时代,无论如何叫喊,也是在现代物理的大门之外。
现实就是如此的不以人们的主观愿望而转移。
无论是批广义相对论也好,保广义相对论也好,作为现代物理学革命的导火线,也作为第一个成功的经典型范例,广义相对论作为最重要的环节的历史地位是任何理论和任何人所无法否定的
www.wuli.ac.cn/fileup/PDF/19840501.pdf
轉為繁體網頁
轉為繁體網頁
由 KG Wilson 著作 - 1984
1984年5月1日 - 渐转到1971一1972年论述重整化群的文章.最 .... 重整化群近似就是依次积分掉涨落, 从原子标. 度的涨 ..... 一M彻) 应按波包函数的@) 的集合来进行.负幂律分布 - 英语单词大全 - 911查询
danci.911cha.com › 英语单词大全
轉為繁體網頁
首次提出泥石流规模的负幂律分布的产生的主要根源是汇流过程的自组织临界性。 2
danci.911cha.com › 英语单词大全
轉為繁體網頁
轉為繁體網頁
幂律分布的英文_幂律分布翻译_幂律分布英语怎么说_海词词典
dict.cn/幂律分布
轉為繁體網頁
投资者集簇规模及股票绝对收益率呈负幂律分布; Both the investor clusters and stock absolute yield obey negative power law. 这叫做幂律分布。 This is called a ...
dict.cn/幂律分布
轉為繁體網頁
轉為繁體網頁
主题:请教幂律分布与负指数分布的关系,以及长尾分布属于哪 ...
cos.name › ... › 讨论区 › 统计学世界 › 数理统计
轉為繁體網頁
2011年8月26日 - 请教幂律分布与负指数分布的关系,以及长尾分布属于哪一种?我看到两个地方把长尾分布分别说成负指数分布和幂律分布的. 2014年7月23日 ...
cos.name › ... › 讨论区 › 统计学世界 › 数理统计
轉為繁體網頁
轉為繁體網頁
负指数分布_百度百科
baike.baidu.com/view/1868401.htm
轉為繁體網頁
负指数分布又称指数分布。泊松事件流的等待时间(相继两次出现之间的间隔)服从指数分布。 ... 负指数分布比幂分布趋近0的速度慢很多,所以有一条很长的尾巴。 ... 幂
baike.baidu.com/view/1868401.htm
轉為繁體網頁
轉為繁體網頁
负幂律分布
负幂律分布 网络例句
1. It is proposed that the root cause of the power-law distribution function of scale of debris flow is the self-organized criticality underlying flowing together process.
首次提出泥石流规模的负幂律分布的产生的主要根源是汇流过程的自组织临界性。
2. Because the system that has self-organized criticality has two important tokens, those are a power-law frequency-area distribution and long correlation in temporal area.
由于自组织临界性的系统有两个主要表征,即在时间域上的负幂律分布和长程相关性。
3. By statistical computation we prove that the confluence process of Jiangjia Ravine obeys the power-law frequency-area distribution.
本文通过统计计算得到,蒋家沟泥石流汇流和流量过程在暴发频率与泥石流总径流量上服从负幂律分布。
4. By 2-D CA model simulation, we get simulative data. And we use statistical computation and relativity analysis for the first time. So we make the conclusion that the simulation system obeys the power-law frequency-area distribution by improved 2-D CA model.
通过改进的二维沙堆自动机模型的构建和模拟,本文得到了一系列模拟数据,并在此基础之上,首次通过统计计算和相关性分析,得到如下结论:(1)改进的二维沙堆自动机所模拟的系统在沙粒暴发频率对暴发规模的关系上服从负幂律分布。
5. The creative works of this dissertation are as follows: The general model of nonlinear economic systems is developed; The classification of nonlinear economic systems is introduced according to different standard; The statistical forecasting method for nonlinear economic systems is put forward; The statistical cycling theory of nonlinear economic systems is presented; The conditions for the emergence of the statistical cycling of the monopoly, oligopoly, non-complete competition and competition models are studied; The unified description for the formation mechanism of the power law, with negative exponent is obtained by using the fractal theory; The nonlinear formation mechanism of the income distribution is studied.
本文的创新之处在于:①建立了非线性经济系统的一般模型;②按不同的标准,对非线性经济系统进行了分类;③提出了非线性经济系统的统计预测方法;④提出了非线性经济系统的统计周期理论,⑤研究了完全垄断、寡头垄断、不完全竞争和完全竞争经济系统宏观状态出现统计周期性的条件;⑥用分形理论对负幂律分布的形成机制进行了统一描述;⑦研究了收入分布的非线性机制。
6. We find out that the relative importance has nothing to do with some basic statistical characteristics, such as volatility clustering, sharp peaks and fat tail distributions of stock yield. Both the investor clusters and stock absolute yield obey negative power law. The change of relative importance influences fractal feature of stock yields.
研究结果表明,变化的网络密度和股价波动状况权重系数,不影响股票收益率分布的非正态、尖峰厚尾和收益率波动聚集等特征;投资者集簇规模及股票绝对收益率呈负幂律分布;权重系数的变化会影响股票收益率的分形特征。
7. The general model and classification of nonlinear economic systems are introduced. Based on the general model, the micro mechanisms of macro states of discrete and continuous nonlinear economic systems are discussed respectively and some general conclusions are obtained. The analyses of monopoly, oligopoly, non-complete competition and competition models are made respectively by applying those conclusions. The conditions of coexistence of cooperation and competition and statistical cycling of macro states of nonlinear economic systems are discussed and the statistical forecasting method is introduced. Applying the conclusions, the coexistence of cooperation and competition on Internet is discussed. The power law with negative exponent is a quantitative description of the relation between the macro state and the micro mechanism. At last, using the fractal theory, the formation mechanisms of power law with negative exponent are studied and the conclusions are used on the analysis of income distribution.
首先建立了非线性经济系统的一般模型,并对非线性经济系统进行了分类,在此基础上分别对离散型和连续型非线性经济系统的宏观状态演化和微观机制的关系进行了探讨,得到了具有一般意义的结论,然后将这些结论应用于完全垄断、寡头垄断、不完全竞争和完全竞争经济系统的分析中,讨论了在非线性经济系统中竞争与合作共存、宏观状态出现统计周期性的条件,提出了非线性经济系统的统计预测方法,并将这些理论和方法初步应用于分析计算机互联网中竞争与合作共存的情形,负幂律分布是非线性经济系统宏观状态与微观机制关系的一种定量描述,在论文的最后,应用分形理论,研究了负幂律分布的形成机制,并将得到的结论应用到收入分布的分析之中。
首次提出泥石流规模的负幂律分布的产生的主要根源是汇流过程的自组织临界性。
2. Because the system that has self-organized criticality has two important tokens, those are a power-law frequency-area distribution and long correlation in temporal area.
由于自组织临界性的系统有两个主要表征,即在时间域上的负幂律分布和长程相关性。
3. By statistical computation we prove that the confluence process of Jiangjia Ravine obeys the power-law frequency-area distribution.
本文通过统计计算得到,蒋家沟泥石流汇流和流量过程在暴发频率与泥石流总径流量上服从负幂律分布。
4. By 2-D CA model simulation, we get simulative data. And we use statistical computation and relativity analysis for the first time. So we make the conclusion that the simulation system obeys the power-law frequency-area distribution by improved 2-D CA model.
通过改进的二维沙堆自动机模型的构建和模拟,本文得到了一系列模拟数据,并在此基础之上,首次通过统计计算和相关性分析,得到如下结论:(1)改进的二维沙堆自动机所模拟的系统在沙粒暴发频率对暴发规模的关系上服从负幂律分布。
5. The creative works of this dissertation are as follows: The general model of nonlinear economic systems is developed; The classification of nonlinear economic systems is introduced according to different standard; The statistical forecasting method for nonlinear economic systems is put forward; The statistical cycling theory of nonlinear economic systems is presented; The conditions for the emergence of the statistical cycling of the monopoly, oligopoly, non-complete competition and competition models are studied; The unified description for the formation mechanism of the power law, with negative exponent is obtained by using the fractal theory; The nonlinear formation mechanism of the income distribution is studied.
本文的创新之处在于:①建立了非线性经济系统的一般模型;②按不同的标准,对非线性经济系统进行了分类;③提出了非线性经济系统的统计预测方法;④提出了非线性经济系统的统计周期理论,⑤研究了完全垄断、寡头垄断、不完全竞争和完全竞争经济系统宏观状态出现统计周期性的条件;⑥用分形理论对负幂律分布的形成机制进行了统一描述;⑦研究了收入分布的非线性机制。
6. We find out that the relative importance has nothing to do with some basic statistical characteristics, such as volatility clustering, sharp peaks and fat tail distributions of stock yield. Both the investor clusters and stock absolute yield obey negative power law. The change of relative importance influences fractal feature of stock yields.
研究结果表明,变化的网络密度和股价波动状况权重系数,不影响股票收益率分布的非正态、尖峰厚尾和收益率波动聚集等特征;投资者集簇规模及股票绝对收益率呈负幂律分布;权重系数的变化会影响股票收益率的分形特征。
7. The general model and classification of nonlinear economic systems are introduced. Based on the general model, the micro mechanisms of macro states of discrete and continuous nonlinear economic systems are discussed respectively and some general conclusions are obtained. The analyses of monopoly, oligopoly, non-complete competition and competition models are made respectively by applying those conclusions. The conditions of coexistence of cooperation and competition and statistical cycling of macro states of nonlinear economic systems are discussed and the statistical forecasting method is introduced. Applying the conclusions, the coexistence of cooperation and competition on Internet is discussed. The power law with negative exponent is a quantitative description of the relation between the macro state and the micro mechanism. At last, using the fractal theory, the formation mechanisms of power law with negative exponent are studied and the conclusions are used on the analysis of income distribution.
首先建立了非线性经济系统的一般模型,并对非线性经济系统进行了分类,在此基础上分别对离散型和连续型非线性经济系统的宏观状态演化和微观机制的关系进行了探讨,得到了具有一般意义的结论,然后将这些结论应用于完全垄断、寡头垄断、不完全竞争和完全竞争经济系统的分析中,讨论了在非线性经济系统中竞争与合作共存、宏观状态出现统计周期性的条件,提出了非线性经济系统的统计预测方法,并将这些理论和方法初步应用于分析计算机互联网中竞争与合作共存的情形,负幂律分布是非线性经济系统宏观状态与微观机制关系的一种定量描述,在论文的最后,应用分形理论,研究了负幂律分布的形成机制,并将得到的结论应用到收入分布的分析之中。
分形之父芒德勃罗(3)
发布时间: 2013/5/24 10:10:43 被阅览数: 106 次 来源: 哲学网 |
| 4.进出经济学 现在查到芒德勃罗一共发表18篇经济学论文(也许会有几篇的出入),发表时间集中在1959年至1973年。综观芒氏的论文和专著,他只关心一个核心的经济问题——收入分布以及与之有关的价格问题。据他本人讲,他对经济学中的帕累托(Vilfredo Pareto,1848—1923)分布的研究从1957年在哥伦比亚大学和康奈尔大学的时期就开始了,然后在法国里尔大学和综合工科学校继续了这项工作。1973年以后他义无返顾地离开了经济学,专心发展“分形几何学”。与在其他学科一样,经济学界并没有轻易接受他的非正统观点,但芒德勃罗已经得到自己想得到的东西,他并不在乎经济学界当时能否承认他。 芒德勃罗的经济学研究在经济学团体内引起过两次巨大风波,一次是在60年代末,一次是在80年代末。第一次是因为芒氏的观点攻击了当时占支配地位的计量经济学和资产定价理论,第二次是因为芒氏在非线性动力学运动中出尽风头,经济学家受“混沌”的影响,间接评论了芒氏的早期研究工作。两次反响的主流都是怀疑芒氏的理论和方法,即使有一些人受芒氏论文的激励,转而注意自己未曾考虑的方面,也不相信芒氏的理论。 芒德勃罗最早关注经济学问题是从关于收入分配的帕累托定律(Pareto’s law)开始的,这个定律的形式颇像他在语言学词频分布中注意到的齐普夫定律(G.K.Zipf’s law)。意大利经济学家帕累托曾专门分析过收入分布数据,他发现收入分布具有如下特点:收入水平越高,则收入高于这一水平的人口越少。他当时认定收入分布对于人为干预是不变的。芒德勃罗的经济论文发表后,经济学界不以为然。正统经济学家认为数据拟合得并不佳,并且认为芒氏的理论需要微观证据。芒德勃罗看重的不是数据拟合到何种程度, 而是收入分布的长时尾(fattai-ls)现象在尺度变换下具有不变性,即个人收入分布、厂商尺度的收入分布和城市尺度的收入分布都具有这样的“尾巴”。“长时尾”现象暗示存在一种非高斯意义上的稳定分布。芒德勃罗熟悉他老师莱维的工作,立即将它与莱维的“稳定分布”联系起来。 简单说来,稳定分布的含义是,多个独立同分布随机变量序列经过适当的线性总和后,其分布仍然保持不变。稳定分布是无穷可分的,对应于稳定分布的随机过程是稳定过程。稳定分布是比正态分布更广泛的一类分布,其中包含了正态分布。标准正态分布与正态分布都是稳定分布,柯西分布也是一种稳定分布,除此之外还有没有别的重要的稳定分布呢?这正是芒德勃罗急于思考的。 芒德勃罗的经济模型中具有尺度变换下的“不变性”,他认为这十分关键,仅仅凭这一点就值得认真研究。他认为负幂律分布是除了高斯正态稳定分布外最简单、最值得考虑的一种稳定分布。它就像玻意耳(Boyle)的气体模型一样,可能与实际有些差别, 但它是一种重要类型,一种简单的理想情况,只有研究清楚了这种理想情况,才能推而广之从而考虑更复杂的情形。正如我们不能说理想气体(id eal gas)模型没有价值,也不能说帕累托-莱维分布过于理想化而没有实用价值一样。从这种意义上看,经济学界对他的反驳其实均不构成威胁。芒德勃罗是从逻辑分类的角度、从数学可能性的角度思考问题的,其模型撇开经验事实仍然具有理论价值。实际上1963年洛仑兹(Edward Lorenz,1917—)的《确定性非周期流》一文(在非线性科学史上具有重要地位)也具有此性质,洛仑兹方程只是大气运动的一种极度的理论抽象和简化,它甚至可以与实际的大气运动无关,但仍然具有重要理论意义和间接的实际意义。也正因为如此,芒德勃罗与洛仑兹的理想模型的应用也就不限于什么经济学或者气象学,而具有普遍性,可以扩展到相当多的学科。芒德勃罗实际上也是这样做的,他不久后就将莱维稳定过程用于湍流研究,特别强调了“莱维飞行”,现在看来他的确是先行者,历史将公正地记录下他的先驱性工作。 以棉花价格波动为例来讲,芒德勃罗的理论的特点在于,它不是考虑在某一个特定层次产生价格变动的规律,而是跨越层次,寻求尺度变换下的不变性。棉花价格是一种理想的数据源,经济学家对其变动的传统看法是,短期变化与长期变化没有关联,由快涨落导致的瞬间价格变化是随机的,而长期的价格波动是由于显然的宏观经济形势和战争之类重要事件决定的。因此传统经济学处理此问题的办法是,在确定性的过程中加上随机的噪声。芒德勃罗却把不同层次统一起来,发现日变化曲线与月变化曲线的一致性。对于股票价格,他也作了类似的分析。这未必是最好的理论方法,但至少是一种可能的理论方法,而以前人们确实忽视了它。但经济学界由于长期习惯于自己那一套思路,对芒氏的做法自然有反感,攻击他的最好办法就是指出其曲线拟合不理想。 在研究股票价格变化中,芒氏极为反对“价格连续变化”的模型,认为这种照搬牛顿力学于经济学不济于事。在经济系统中,小的连续变化可以引起突然的不连续变化。基于这种考虑他否定了滤波预测方案和各种人为凑出高斯分布的办法。在经济学研究中他提出了标度原理。 设X(t)为价格,logX(t)是独立增量过程,即logX(t+d )-logX(t)具有独立于d的分布,其中只需引入一个标度因子。芒氏立即想用此模型得出一些有意义的结果,但首先要面对的是这种模型的奇怪性质(实际上这竟是他所期望的)。芒氏大胆地假设logx(t+d )-togx(t)“无穷方差”!他第一次用符号V表示方差。以前人们想当然地假设方差是有限量,发散的情况根本不予考虑,也不应该考虑。用芒氏语言讲,人们似乎患了“无穷方差综合症”。具有反叛色彩的芒氏假定V=∞自有他的考虑:“不用说,假定υ=∞的成功后果是, “我就很容易使曲线具有无穷长度、曲面具有无穷面积。”于是后来提到的“英国海岸线长度”、皮亚诺曲线填充、柯赫雪花曲线长度等问题都有了理论基础,当然其他思想渊源也曾帮助他得到了那些结果。但作者认为,海岸线问题是后来的事。那时他已经有了基本结论,他不断翻阅数学“故纸堆”,也不断发现一些阐述得更佳的论述,但这些新发现的材料当初对于他形成基本的分形思想并未产生影响。在撰写专著时,他当然要重新规划,以一种更直接、更通俗、更符合逻辑顺序(发现过程并不符合通常的逻辑)的方式叙述出来,甚至更多的是考虑读者的反应。 到了80年代经济学界受非线性动力学的影响不得不对芒氏的早期研究作出评介,在此之前克拉克(P.Clark )的博士论文以及后来的自回归条件异方差(ARCH)、广义自回归条件异方差(GARCH )模型回避了芒德勃罗开创的路线,仍然假设噪声服从于一种基本的高斯分布,但有一个变化的二阶矩。他们的文章引用了芒氏的假设,但设法避免那类假设。但这种处理方法仍然没有逃出分数阶自回归滑动平均(ARIMA )的套路。到后来,许多经济学家更多地采用GP关联积分算法求时间序列的分维数,用BDS统计(Brock—Dechert—Scheinkman 三人在关联积分的基础上发明的)检查经济系统中是否存在非线性结构。但是正如米诺夫基指出的,经济学界的这些人物并没有认真吸收芒德勃罗的思想,而是应付、回避矛盾,他们既排斥莱维稳定分布也排斥混沌。芒德勃罗早已摒弃了“不是决定论就是随机论”的两极化选择,他认为经济现象比较复杂,应当用更精致的随机过程或者混沌动力学描述,应当放弃牛顿经典力学的套路:由原子运动推出一切。本质上在经济学问题上芒德勃罗采用的是一种类似统计物理/热力学的现象学的方法,这一性质还未被经济学界深入理解。 当芒德勃罗离开经济学时,他得到了什么?他似乎高兴地带走了价格变动的自相似观点、标度律的观点,以及一种似乎无人注意但有着各种潜在应用价值的“莱维稳定分布”。 |



No comments:
Post a Comment