麦克斯韦方程组是如何来的?
2015-03-17 00:00:00 来源: 译言网 跟贴 0 条 手机看新闻美国著名物理学家理查德·费曼(Richard Feynman)曾预言:“人类历史从长远看,好比说到一万年以后看回来,19世纪最举足轻重的毫无疑问就是麦克斯韦发现了电动力学定律。”这个预言或许对吧。可是费曼也知道,麦克斯韦可不是一下子就发现了所有有关电动力学的定律,所以如果一定要选出一个有代表性的时间,他很有可能会选1864年10月27日。那天麦克斯韦向皇家学会成员阐述了他的论文“电磁场的动力理论”。一年后麦克斯韦正式发表他这个激进的新理论。那时候整套理论还显得很冗长,后来是他的追随者把这个理论精炼到了四个如今著名的方程式。无论如何,把这些方程是称为麦克斯韦方程组还是有道理的。所以我们今天要来庆祝它们150岁的生日。
1820年以前,科学家相信电和磁是截然不同的两种现象。后来汉施·克里斯蒂安·奥斯特(Hans Christian Oersted)报告了一个引人注目的结果:当他把磁化的指南针放到通电导线附近时,指南针移动到了和导线垂直的角度。各处的科学家都惊呆了,立即着手研究电和磁的关联。其中就有麦克·法拉第(Michael Faraday)。

法拉第是个伦敦铁匠的儿子,自学成材。29岁的时候,他在皇家研究所汉弗莱·戴维(Humphry Davy)手下工作。作为一个分析化学家,他竖立了机智灵敏又可靠的好口碑。只有其他事情一做完,他就开始实验电流和磁。他并不懂数学,所以至少表面看来,他比起那些同时代的接受过完好教育的人来有所欠缺。但反过来说,这种缺失却成了他的优势,他比别人更能自由地思考。他问了很多别人都没有考虑过的问题,设计了别人没有想到过的实验,看到了别人错过的机会。
与他同时代的安德烈·玛丽·安培(André Marie Ampère)以惊人的速度重复了奥斯特的实验。没几个月就发展出了一整套数学理论。他说,任何一个电流环都会产生贯穿过这个环的磁力。安培的理论,就像此前的库伦,是基于牛顿的万有引力理论的。库伦认为,在点电荷和磁极之间会即时产生直线状的电力和磁力。这些力和距离的平方成反比。安培计算了把通电导线看作是极小电流分段串在一起,每个极小电流分段当作是一个点来处理,从而计算通电导线产生的磁力。要算通电导线产生的磁力,只要把所有电流分段的效应在数学上简单相加。
在法拉第看来,若要说奥斯特实验中指南针是被一组直线引力以及它和导线之间排斥力驱动,那是不对的。他觉得,应该是通电导线在它的周围空间引起了一种环形的力。他涉及了一个聪明而简单的实验,验证这个想法。法拉第将一条此贴竖直固定在一个小脸盆中央,并将水银倒入脸盆中,直到只有磁铁的顶端露出来。然后他把一根导线伸到水银中。当他通上电,导线和水银就是电路的一部分了。导线末端接触水银的地方很快地绕着磁铁转圈。他制造了这个世界上第一个电动机。
安培已经演示过如何从电产生磁——那么从磁里产生电当然应该有可能啦。然而十年来科学家屡试屡败。然后到了1831年,法拉第发现了这个目标难以企及的原因:要想在导线里产生电流,你必须改变导线周围空间里的磁场态。你只要在电路周围移动一个磁铁(或者反过来),那么电路就有电流了。然而空间的磁场态确切来说到底是什么呢?法拉第想起了白纸上磁铁周围铁屑的分布,他确信磁铁不只是一块带着有趣特性的铁,它是整个磁力曲线在空间分布的中心,磁力线实际存在。而且,这种现象不仅铁磁有:在导电电路的周围也有相似的磁力线。
法拉第得出进一步结论。通过测试,他总结说每个带电物体都是电力线的源头,在空间里也会弯曲。和连续成环状的磁力线不同(它们不终止于磁铁,而是穿过磁铁),电力线总是从一处的正电荷物体到另一处的负电荷物体。所以每个正电荷都和别处一个负电荷有一个平衡。他同时观察到,无论是磁效应还是电效应,都不是即时的,都要一段时间来产生作用。照他的理解,这是系统要建立起这些电力、磁力线所需要花费的时间。

法拉第和其他科学家的思维方式很不一样。通常科学家仍然认为电力和磁力是由一段距离内的实质物体相互作用,而空间的作用是消极的。皇家天文学家乔治比德尔艾利(George Biddell Airy)爵士评价法拉第的电力磁力线是“模糊和变化的”,他代表了当时很多人的意见。这也好理解。他们理解的距离间相互作用这个理论有一个明确的公式,而法拉第的理论却没有提供任何公式。虽然他们尊敬法拉第,认为他是一位超凡的实验家,但大多数科学家觉得他不懂数学,因而缺乏理论基础。
法拉第了解他们的这些意见,所以在发表电力磁力线理论的时候格外谨慎。只有一次他做了一次冒险。那是在1846年, 他的一个同事查尔斯·威特斯通(Charles Wheatstone)要在皇家学院演讲他的发明,但临阵怯场。于是,法拉第决定自己来做个演讲。他在给定时间结束前开始讲预告之外的内容。他卸下心理防备,把自己最私密的想法说了出来。他向听众们讲述了有着惊人预见的关于光的电磁理论。他推测,全部空间都充满着电力线和磁力线。这些线横向振动,当受到干扰时,就会沿着线的方向以很快但有限的速度发射能量波。他说,光很可能就是光线振动的一种体现。
现在我们知道,他已经很接近真相了。但在法拉第的那些科学家同事看来,光线振动就像奇幻传说一样荒唐。以至于法拉第的支持者都感到尴尬,法拉第本人也后悔松懈了思想防备。他把他同时代的人远远地甩在了后头,一直等到四十年以后才有人能揭示法拉第真正的伟大。这个人有着同样思想高度,和法拉第能力上的有着互补。这个人就是詹姆士·克勒克·麦克斯韦(James Clerk Maxwell)。
麦克斯韦职业生涯惊人而又短暂(他死时48岁)。他在他从事的每个物理分领域都做出了根本性的发现。但他最伟大的工作是关于电场和磁场,这点像法拉第。麦克斯韦出生于一个高贵的苏格兰家庭,他进了爱丁堡最好的中学,然后去了爱丁堡大学和剑桥大学。他在剑桥大学得到了数学荣誉学位考试的第二名,获得了学士学位。这之后,他就开始阅读有关法拉第的电学实验。麦克斯韦一下子被法拉第的坦诚吸引了:这个伟人公开他的成功以及失败,表达他成熟以及粗略的想法。再读下去,麦克斯韦看到这项工作真正的力量:在寻找探究明白前,思想就有伟大飞跃。在麦克斯韦看来,线这个概念在空间上是有道理的,虽然法拉第表达起来都是用文字的,但本质上这是可以用数学表述的。他开始用数学的力量承载起法拉第的想法。九年里,他跨越了三次令人惊叹的阶段,成功了。
麦克斯韦非常善于发现自然界不同领域的相似性。1856年,他开始用虚拟的不可压缩的匀速流体来类比电力线和磁力线:在空间区域的流体速度和方向代表了力线的密度和方向。如此,他就证明了静态电力和磁力可以从传统的距离之间的作用理论推导出来。这是个了不起的成就。但当时,麦克斯韦不知道如何处理变化的力线。依照他惯有的方式,他去干别的工作了,但这些想法一致在他脑中酝酿。
六年后,他得到了一个新模型。他想象空间里充满着小球,这些小球可以旋转,他们被更小的粒子在空间上隔开。那些小粒子就像是钢珠轴承。麦克斯韦假设这些小球有很小但有限的质量,有一定的弹性,这就可以把电力线和磁力线和机械系统作对比。因而任何一个小球的变化引起了其他小球的变化。这个杰出的模型导出了所有关于电磁的著名方程,它预言电磁波的传播速度只由电磁基本性质决定。这个速度和测到的光速只相差1.5%。这是个惊人的结果,但科学家却都没表态。他们相信,任何物理领域,都是以认清自然真实规律为目标的。他们觉得麦克斯韦的模型并没有原创性,用这个模型尝试对电磁和光作解释是有缺陷的。所有人都预计麦克斯韦下一步就是要完善这个模型。但他没有,他把模型放到一边,只运用动力原理,从头开始搭建这个理论。
两年后,成果发表在“电磁场的动力理论”这篇论文中。这个模型认为,无处不在的媒介有惯性和弹性,但没有特别的机械性质,它们取代了旧模型中的小球。就像变戏法一样,他运用了约瑟夫·路易斯·拉格朗日(Joseph Louis Lagrange)的办法,把动力系统看成一个“黑盒子”:只要描述了这个系统的一些通常特征,就可以在不知道具体机理的情况下,通过输入推导出输出。如此,他就有了电磁场方程组,一共有20个方程。1864年10月,他在皇家学会讲述他的这篇论文,听众们简直不知道该拿它如何是好。一个理论建立在奇怪的模型上已经够糟糕了,而一个理论不以任何模型为基础,那就根本无法理解。
直到1879年麦克斯韦过世,又过了数年,他的理论都没有人能够真正理解,就好似在玻璃箱中的展示,广受赞誉却无人能够接近。后来是自学成才做过电报员的奥利弗·亥维赛,他让这套理论变得可以亲近。1885年,他把这套理论总结为我们现在所称的四个麦克斯韦方程

这里 E 和 H 分别是空间任意点电场力和磁场力的矢量。 ε 和 μ 分别电和磁的基本常量,ρ是电荷密度, J是电流密度矢量。头两个方程简洁表述了电和磁的平方反比定律。第三、四个方程定义了电和磁之间的关系,说明电磁波存在并以1/√(με) 的速度传播。
亥维赛运用矢量分析大大简化了方程表达。三维矢量用一个字母表示,把电能和磁能都放进了背景里的媒介中。 1888年海因里希·赫兹(Heinrich Hertz)发现电磁波极大地推动了人们对电磁理论的兴趣。当时,人们求助于亥维赛的精炼版本,而非麦克斯韦最初的表达。
要把故事讲完整,还要加上三点内容。第一,麦克斯维其实很容易就可以把理论简化压缩,但是他觉得最好还是保持一定的开放性。许多年后,他的智慧显现了:理查德·费曼和其他人发展量子电动力学,就是利用了被亥维赛剔除的原始量,从而。第二点,是麦克斯韦命名了运算符号,比如散度和旋度。第三,麦克斯韦事实上在他的《关于电和磁的论文》一文中已经用了适量,只不过他把矢量表达看作是一种额外的选择。他的矢量是从威廉·罗万·哈密顿(William RowanHamilton)复杂的四元数推导而来。大多数人都不想用这么复杂的矢量系统,直到亥维赛推出简便许多的系统他们才开始接受。
最后想想这点:虽然麦克斯韦从来没有刻意去追求,但他的方程组揭示了光速是1/√( με),和观察者、光源的相对速度都没有关系。这引导出了爱因斯坦的狭义相对论, E = mc²。 所以说,或许这个世界上最著名的公示就应该是 E = m/με。这样才能体现爱因斯坦和麦克斯韦共同的贡献。
巴斯马宏(Basil Mahon)撰写了若干本关于詹姆士·克勒克·麦克斯韦、麦克·法拉第以及奥利弗·亥维赛的书。他最新和南希·福布斯(Nancy Forbes,)合作的的一本书《Faraday, Maxwell, and the Electromagnetic Field 》由Prometheus Books出版 (ISBN 978-1-61614-942-0).
e-mail basil.mahon@tiscali.co.uk
参考书目
(本文来源:译言网 )
梯度、散度、旋度、其常用公式、與正交(球、柱)座標系
向量微分
純量場微分與梯度
溫度場、高度(海拔)、氣壓場(場是空間的分佈)保守向量場
W = ∫ab F · ds向量微分算子 ∇ (讀做 nabla 或 del)
保守力作功,僅與初、末位置有關,而與路徑無關。即上式
W = ∫ab F · ds = U(b) - U(a)
這意味著 F · ds = dU,即存在 一 U(x1, x2, x3),其
dU = (∂U /∂x1) dx1 + (∂U /∂x2) dx2 + (∂U /∂x3) dx3
= ( ∂U /∂x1 , ∂U /∂x2 , ∂U /∂x3 ) · (dx1, dx2, dx3) = (∇U) · dr
∇ ≡ ( ∂/∂x1 , ∂/∂x2 , ∂/∂x3 )向量場的向量微分
散度
∇· A = ( ∂/∂x1 , ∂/∂x2 , ∂/∂x3 ) · (A1, A2, A3)
= ∂A1 /∂x1 + ∂A2 /∂x2 + ∂A3 /∂x3
是一個純量
散度的意義:
如果一個向量場是由某種 "源" 所產生的,那麼這個場在空間處處的的散度值會突顯出該 "源" 存在與否。
從連續方程式理解 "散" 度
自行見課本說明,會考。
∇2
∇2 φ = 0 叫 Laplace 方程式,重要。
∇2 作用在向量場與純量場都可以。
旋度
善用 εijk 定義 處理下列證明
∇ × ∇φ = 0
用到 εijk 的反對稱性,也就是 εijk = -εikj 。
常用公式
正交曲線性座標系
作業:驗證上列十五個公式。(公式 (6) 最後一個 × 應作 · )
提示:善用 εijk 與 δij 等關係式
見課本推導,關鍵概述如下:常用正交座標系
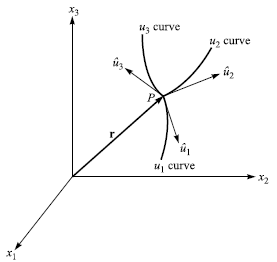
首先,在不失一般性的情況下,任何座標變換總是存在新、舊座標位置的定義:新座標軸的產生
見圖 1.16
上面這一組的三個函數,會把體的任一點對應到另一點,佈滿三維空間。
這裏如果我們固定住 u2, u3 而只讓 u1 動,就能掃描出一條空間曲線,就可以把它們的切線向量,拿來作為座標軸的方向,就像於前單元採用單一 t 或弧長 s 作為參數時,可定義切線方向及單位切向量那樣。(至於這樣做出來的座標軸單位向量,並不保證正交。)
小線段元素的變換
小體積元素的變換
把 ∂r /∂ui 的方向定為 ui^,長度 |∂r /∂ui| 定為 hi (又叫 scale factor),則上式成為
我們現在規定 u^1, u^2, u^3 互為正交,現在再來看小體積元素如何變換
重點是:變換時,乘上 Jacobian。
Jacobian 不等於 0 時,局部有 1對1 轉換 (這是課本提醒)。
(為什麼要講這個?因為未來會有需要把 ∫ f(x,y,z) dxdydz 換成 ∫ f(u1,u2,u3) J du1du2du3 時,就要在微小體積元素上乘上 J。)
梯度算子、散度算子、旋度算子、拉卜拉斯算子的變換 (即它們在非卡氏座標系的公式)
通式
梯度
先看結果公式散度預備
推導起點
假設
注意 fi 不是本節一開始 談到之 座標變換函數 f, g, h ,而是某函數梯度之分量。
前有
由於 u^1, u^2, u^3 自成一 "正交歸一" 座標系 (這是前提假設),故有 (用上面 ∇φ 的公式與 dr 的公式)
但又根據全微分之基本定義,下式一定成立
綜合前兩式條件,即得
hi fi = ∂φ/∂ui,即 fi = (1/hi) ∂φ/∂ui
得證原式
補充:hi 是有幾何學上的意義的,詳見其他教科書。
會利用到的兩個關係散度
(a) 的證明
利用前已證之 ∇φ 公式,套用在 u1 上, ∇u1 = (1/h1) (∂u1/∂u1) u1^ + 0 + 0 = (1/h1) u1^,故 其長度 | ∇u1| = 1/h1。(b) 的證明
由 (a) 我們有 ∇u1 = (1/h1) u1^ ,∇u2 = (1/h2) u2^,∇u3 = (1/h3) u3^
∇u2 × ∇u3 = 1/(h2 h3) u2^ × u3^ = 1/(h2 h3) u1^
(為什麼 u2^ × u3^ = u1^ ? )
故 u1^ = h2 h3 ∇u2 × ∇u3 ,得證。
證法
∇ · A = ∇ · (Σi Ai ui^) = ∇ · ( A1 u1^) + ∇ · ( A2 u2^) + ∇ · ( A3 u3^) (分配律)
其中先看 ∇ · ( A1 u1^)
利用前面的 u1^ = h2 h3 ∇u2 × ∇u3 ,有
∇ · ( A1 u1^) = ∇ · ( A1 h2 h3 ∇u2 × ∇u3 )
= ∇( A1 h2 h3) · (∇u2 × ∇u3 ) +( A1 h2 h3) ∇· ( ∇u2 × ∇u3 )
再利用前面的 ∇ui = (1/hi) ui^
上式 = (1/h1) (∂ A1 h2 h3 / ∂ u1) [1/ (h2 h3)] + 0
第二項為零是因為使用了"對任何函數 f, g , ∇· ( ∇f × ∇g ) = 0 " 這一個特性。(同學們自己可利用 ∇· ( A × B ) = ... 的公式證明看看 (用前面 15 條公式之 (4) 和 (6) ),不會做可見 Riley 書。)
(亦可由 ∇u2 × ∇u3 = (u^2/ h2) × (u^3/ h3) = u^1/ (h2h3),
(課文提供的證法,較不方便的點也在此。因為既要證明∇· ( ) 的形式,且尚未證出,就又需要 用到∇· ( ) 的公式。)
補充:也可使用 ∇· A ≡ limΔV→0 (∫CS A · ds ) / ΔV ,即微小體積的通量(向量面積分)來理解 ∇· (u1^) = 0 的理由。
思考:為什麼 ∇不是用向量分量的轉換公式就好,其解果還這麼複雜? 我們把 ∇寫成向量的樣子,操作規則也很像,它到底是不是向量,若不是,為何與向量如此相像?
詭論式的推導
∇ · ( A1 u1^) = ∇A1 · u1^ + A1∇ · u1^
其中,第一項中的
∇A1 = (1/h1) (∂A1/ ∂ u1) u1^ + (1/h2) (∂A1/ ∂ u2) u2^ + (1/h3) (∂A1/ ∂ u3) u3^
故
∇A1 · u1^ = (1/h1) (∂A1/ ∂ u1)
另外,第二項中的
∇ · u1^ = 0
綜合兩項,
∇ · ( A1 u1^) = (1/h1) (∂A1/ ∂ u1)
與剛才上面導出來的不一樣,那裏見到鬼了?
拉卜拉斯算子
前面已知
組合使用,可得
問題:我們怎麼知道上面的操作是合法的?真的可以這樣套用嗎?為什麼?難到沒有一個 "正統座標轉換" ,或是 "廣義微分定義" 的方法,讓我們可以直接看到上述各通式?
旋度
一樣從 ∇× A = ∇× (A1 u1^ + A2 u2^ + A3 u3^) 開始 看 u1 分量
∇× (A1 u1^) = ∇× ( A1 h1∇u1 )
= ∇( A1 h1) × ∇u1 + A1 h1 ∇× ∇u1 = ∇( A1 h1) × ∇u1 + 0
= ∇( A1 h1) × (u1^ / (h2h3))
= Σijk εijk ui^ [(∂/∂uj ) (A1 h1)] [(u1^/ (h2h3)]|k
= Σijkεijk ui^ [(∂/∂uj ) (A1 h1)] [(1/ (h2h3)]k δ1k
= Σij εij1 ui^ [(∂/∂uj ) (A1 h1)] [(1/ (h2h3)]
= εi=2,j=3,1 ui^ [(∂/∂uj ) (A1 h1)] [(1/ (h2h3)] + εi=3,j=2,1 ui^ [(∂/∂uj ) (A1 h1)] [(1/ (h2h3)]
= u2^ [(∂/∂u3 ) (A1 h1)] [1/ (h2h3)] − u3^ [(∂/∂u2 ) (A1 h1)] [1/ (h2h3)]
= [1/ (h2h3)] [ u2^ (∂/∂u3 ) (A1 h1) − u3^ (∂/∂u2 ) (A1 h1)]
(提醒:看到 × 就代入 εijk ,然後設法讓 εijk 消失,是常見的作法)
課本的作法(倒數第二行括弧內應全是 A1 h1 才對)
綜合三個部分,完整的結果是:
也可寫成行列式形式
問題:我們怎麼知道前面的 (1) ~ (14) 式對曲線性座標系也是對的?
或先問簡單一點:我們怎麼知道 ,那些公式,在另一個卡氏座標是對的?
∇· v、∇× v 、 ∇v 的不變性(進階)
用張量的語言來了解(不同座標下,形式一樣,張量就是在描述這像的東西。)
一本不錯的小書:J. G. Simmonds, A Brief on Tensor Analysis
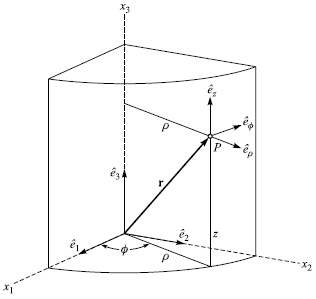
柱座標系
(見課本圖 1.17)
x1 = ρ cosφ, x2 = ρ sinφ, x3 =z
本例中, hrho = 1、hphi = ρ、hz = 1。
證明見下:
方法一
由圖可見方法二
dr = dρ eρ + ρ dφ eφ + dz ez = [1] dρ eρ + [ρ] dφ eφ + [1] dz ez
注意 ρ dφ 的意思。 得證
由圖可見
eρ = cosφ ex + sinφ ey
eφ = - sinφ ex + cosφey
意謂著
ex= cosφeρ- sinφ eφ
ey= sinφeρ + cosφeφ
此外,從 x = ρ cosφ, y = ρ sinφ 的定義,有
dx = cosφdρ - ρsinφ dφ
dy = sinφdρ + ρ cosφ dφ
現在,從 dr = dx ex + dy ey + dz ez 出發,分別代入上面剛剛整理出未的 ex、eφ 及 dx、dy。就可以把 dr 化成全由 dρ、dφ 及 eρ、 eφ 所構成。
dr = dx ex + dy ey + dz ez= (cosφdρ - ρsinφ dφ) (cosφeρ- sinφ eφ) + ( sinφdρ + ρ cosφ dφ ) (ey= sinφeρ + cosφeφ ) + dz ez
利用 cos2θ + sin2θ = 1
最後,得
dr = dρ eρ + ρdφeφ + dz ez
(對行列式乘上一個係數,等同於對其某一行或一列同乘該係數)
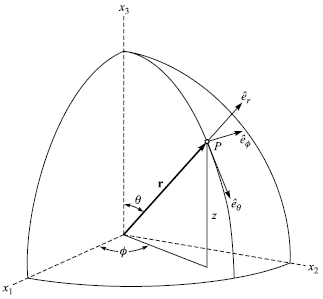
球座標
(見課本圖 1.18)
x1 = r sinθcosφ, x2 = r sinθsinφ, x3 = r cos θ
一樣用 ds2 去對出 h1, h2, h3,見課本
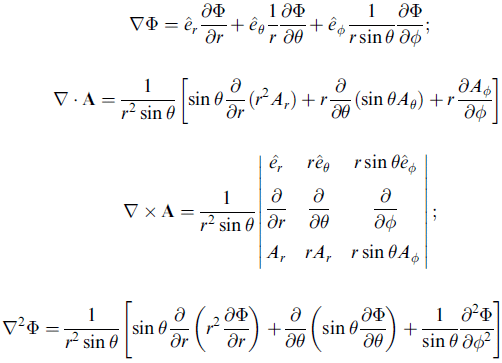
上面的式子雖然很複雜,但數學問題有對稱性時,就會大幅簡化,在未來你們的課程中,這樣的例子很多。
微分運算的核心特徵
(1) 線性 (對函數的加運算組合)
(2) 萊布尼玆律 (對函數的乘運算組合)
說明
想想泰勒展開式
f(x+Δx) = Σ∞n=0 f(n)(x) (Δx)n / n!,其中 f(n)(x) 是函數 f(x) 的第 0 階導數。
欲表達一個連續變化的函數,用微小量的多項式(冪次),配合各階導數(斜率)作展開,總是可以 做到。 而任何微分算子,就是要取出斜率(函數值的變化率)。
現在,試想兩個業經泰勒函數的加法運算組合,要取其一階斜率,自然取得冪次同為 Δx 之各自的一階導數和,故任何微分運算滿足線性。
其次, 試想兩個業經泰勒函數的乘法運算組合,要取其一階斜率,自然取得冪次同為 Δx 之各帶有一次一階導數者(兩個一階導數的那一項,是 Δx2 項,太小),故必滿足 萊布尼玆律。
作業:證明泰勒展開式
參考閱讀
K. F. Riley and M. P. Hobson, Fundation of Mathematics : for the physical sciences, Cambridge University Press
解說清楚,範例眾多。
S. S. Bayin, Essentials of Mathematical Methods in Sceince and Engineering, Wiley
兼具推導詳細與取材完整,
林雲海,基礎數學(簡明版),五南出版社
中文,淺顯易懂
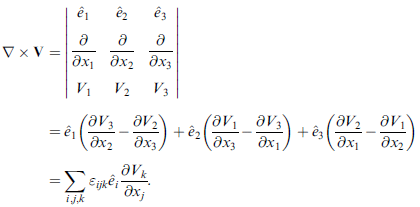
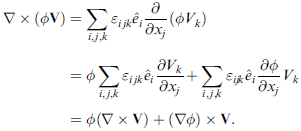

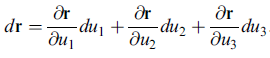

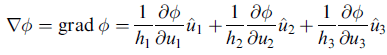
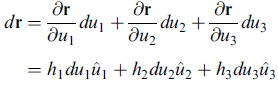
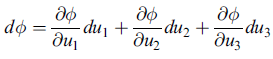
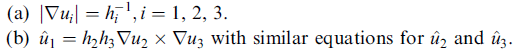
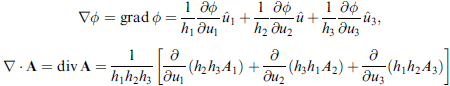
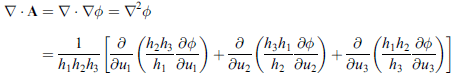
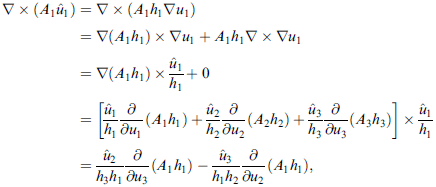
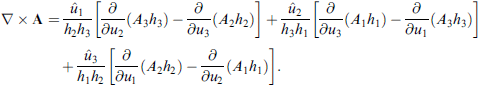
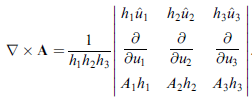
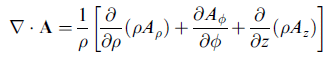
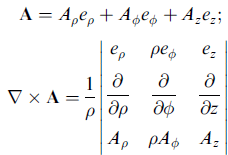
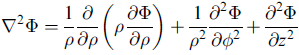
No comments:
Post a Comment