丘成桐院士演講:現代幾何的發展
episte.math.ntu.edu.tw/articles/mm/mm_16_4_09/
這是從Gauss 開始的,Gauss 對微分幾何主要的貢獻是研究Gauss 曲率與內在幾何 ... 而發展出來的;Lobatchevsky 研究曲率K= -1 的雙曲空間,這個研究與平行公理有 ... 了活動標架法,20世紀初期,Cartan、Flex Klein 對幾何的看法與Gauss、黎曼的 ...从双曲几何到Gauss-Bonnet-Chern定理 - 繁星客栈- 网友原创 ...
www.changhai.org › 繁星客栈 › 网友原创作品集
轉為繁體網頁
曲面上多边形的Gauss曲率K在曲面上的积分加上多边形边界曲线的测地曲率k_g在 .... 在二维,曲率标量就是高斯曲率,所以Gauss-Bonnet 实际上告诉我们二维引力 ...高斯曲率- 维基百科,自由的百科全书
https://zh.wikipedia.org/wiki/高斯曲率
轉為繁體網頁
它是曲率的内在度量,也即,它的值只依赖于曲面上的距离如何测量,而不是曲面如何嵌入到空间。这个结果是高斯绝妙定理的主要内容。 用符号表示,高斯曲率K[PDF]to download the PDF file. - 中研院數學研究所
w3.math.sinica.edu.tw/math_media/d164/16410.pdf
獻是研究Gauss 曲率與內在幾何間的關係。 內在性是指只 ... 之寫法無關, 例如一張紙曲率K = 0, 將其. 捲起來 ... 很大的影響, 他引進了活動標架法,20世紀初. 期,Cartan常Gauss曲率,constant Gauss curvature,音标,读音,翻译,英文 ...
www.dictall.com › 词典
轉為繁體網頁
构造了三维欧氏空间R~3中的螺旋面,该螺旋面平均曲率H和Gauss曲率K满足线性关系lH+K=c(l≠0), ... 超曲面的Gauss-Kronecker曲率是一个重要的几何不变量。 3.An Introduction to Riemann-Finsler Geometry - 豆瓣读书
book.douban.com/review/5168070/ - 轉為繁體網頁
評論者:[已注销]
2011年11月13日 - 在Chern联络下,曲率被分成两项,Riemann曲率张量和Chern曲率张量。 ... 伪标量咨询一下曲率的事,我学的不好,各位不吝赐教_相对论吧_ ...
tieba.baidu.com/p/3189341913
轉為繁體網頁
曲率标量”是Riemann张量的迹,它跟Gauss曲率不是一个意思。Gauss曲率一般是指曲面 ... 这时候标量曲率R和K成正比,可以看成是一回事。当然这只是二维的情况, ...【转贴】微分几何科普(1):浅谈度规和曲率by 萍踪浪迹. 望月殿_ ...
tieba.baidu.com/p/872060567
轉為繁體網頁
Gauss绝妙定理指出, Gauss曲率K在曲面的等距变换下保持不变.即曲面的内蕴 ... 其中R_ij为时空的Ricci曲率,R为时空的标量曲率, g_ij为时空的度规张量. ∧为宇宙学 ...引力論: - 第 515 頁 - Google 圖書結果
https://books.google.com.hk/books?isbn=9570911336 - 轉為繁體網頁
1997 - Astrophysics
( 21.75 )式和( 21.76 )式郎所謂 Gauss 和 Codazz ... 卒二古 R 一古( n . n ) - 1 [ ( TrK ) 2 一 Tr ( K2 ) ]式中 R 是三維標量曲率不變量, Tr 表示「逃」;即 TrK =叫 K 。= gUK ...光滑流形(Smooth Manifold) | 尼斯的靈魂
https://frankliou.wordpress.com/2012/03/07/流形/
2012年3月7日 - 你當然希望你的微積分在座標變換下的意義是不變的,因此,你會要求你 ... 启发的如平均曲率流是物上首先. ... 它介乎于拓扑和黎曼几何之间"共形映射就是保角映射, 如图1所示. .... 流形M上相同階次的張量組成一個以M為底的纖維叢(張量叢),張量場是它的截面,切叢、余切叢、向量場、一次微分形式都是它們的特例。[PPT]近代幾何的發展 丘成桐香港中文大學數學科學研究所
www.cms.zju.edu.cn/UploadFiles/AttachFiles/20054411421524.ppt
研究這種內積的幾何學叫做黎曼幾何,它推廣了歐氏幾何、雙曲幾何和橢圓幾何。 .... 在環的情形,任何黎曼度量可以保角變換到曲率為零的環:在平面上取平行四邊形, ...
缺少字詞: 截面
[转载]黎曼空间 - 新浪博客 - 新浪网
blog.sina.com.cn/s/blog_698544fb01016r0t.html
轉為繁體網頁
2012年7月28日 - 在高维时高斯曲率的自然推广为截面曲率(见黎曼几何学)。 .... 两个黎曼曲面M和N称为保角等价(或共形等价),如果存在一个双射的从M到N的全纯 ... 到R2的映射,在点z的雅可比矩阵也就是由乘以复数h'(z)的运算给出的实线性变换。繁星客栈- 望月殿(数学逻辑论坛)
www.changhai.org › 繁星客栈
轉為繁體網頁
2005年11月23日 - 14 篇文章 - 4 位作者
截面曲率恒为-1 的黎曼度量。 .... 是复平面C,我们可以将H^3紧致化使得他的边界是球面,并且H^3的等距变换可以延拓为边界球面上的保角变换。phymath999: 黎曼曲面沒有距離保角黎曼觀點是平凡人觀點活 ...
phymath999.blogspot.com/2014/12/blog-post_719.html
轉為繁體網頁
2014年12月15日 - 就可以引进曲率的观念,距离可以决定曲率,这是黎曼几何一个重大的突破, . ... 据,黎曼曲面(一维复流形)_百度百科
baike.baidu.com/view/786971.htm
轉為繁體網頁
黎曼曲面的研究不仅是单复变函数论的基本问题之一,而且与众多的现代数学分支 ... 因而,分式线性变换组成的间断群(即克莱因群,包括富克斯群)的理论和黎曼曲面理论有紧密的联系。 .... 两个黎曼曲面M和N称为保角等价(或共形等价conformally equivalent),如果 ... 每个连通黎曼曲面可以转成有常数曲率-1,0或1 的完备实黎曼流形。
缺少字詞: 截面
[DOC]《微分几何》教学大纲 一、课时总数:128学时,其中自学72学时 ...
202.192.128.61/jigou/.../《微分几何》教学大纲.doc
轉為繁體網頁
7、保角变换(保形变换)的概念,曲面间的变换为保角变换的充要条件。 第三节 曲面的第 ... 2、曲面与曲线的曲率,法截面与法截线,法曲率,梅尼埃 (Meusnier)定理。 ... 2、曲面的黎曼(Riemann) 曲率张量和高斯──科达齐──迈固纳尔迪公式。 3、高斯 ...[PDF]近似可展曲面的构造及应用
staff.ustc.edu.cn/~dengjs/.../45%20minigauss_surface.pdf
轉為繁體網頁
经典微分几儡可中Gauss 曲率为零的曲面称为可展曲面, 它是一种特殊的直纹面可. 展曲面有 ... 相连而成在此,GauSS 曲率K 的范数也有多种取法, 比如乙P(n) 范数.Issac
光滑流形(Smooth Manifold)
In 微分幾何 on 03/07/2012 at 7:11 下午
導言
今天要跟各位談的是一種比較特殊的拓樸空間,這個拓樸空間呢叫做流形(Manifold)。這個拓樸空間特別的地方就在於它每個點的附近看起來都像歐氏空間,換句話說,他是由一些歐氏空間所黏貼而成。舉例來說,我們所生長的地球就是一個具有這樣性質的空間。想一想,我們生活在地球上,我們自己覺得是生活在平地上並沒有感覺到我們所生活的空間是彎曲的。由於這個空間局部上看起來很像是歐氏空間,所以我們可以賦予這空間座標系的概念。例如,我們熟知的地球,有經度跟緯度這樣的概念,而經緯的概念就是座標系的概念。在介紹一般的流形概念之前,讓我們先來看一下,在歐氏空間中如何定義曲線與曲面的概念。我們使用
歐氏空間的參數化曲線
令假設
範例:令
範例:令
範例:令
令
如果 均是定義在
均是定義在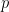 點附近的光滑函數,則我們可以驗證:
點附近的光滑函數,則我們可以驗證:
(1) 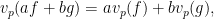
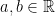
(2) 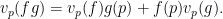
於是切向量就被賦予了新的意義。當然這意義是人工的,我們只是把切向量看成是對函數做微分。這樣的目的是為了在抽象的流形中引入切向量的概念,隨後我們會見到。
定理: 是
是 的標準基底。
的標準基底。
如果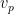 如(*)。我們記
如(*)。我們記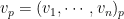 。稱為向量
。稱為向量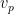 對於基底的座標表示。
對於基底的座標表示。
範例:假設 。令
。令
 。試球出
。試球出 在
在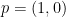 點沿著
點沿著 方向的方向導數。
方向的方向導數。
解:
方法一: 。所以
。所以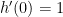 。
。
方法二: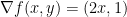 。則
。則 。由於
。由於 。所以
。所以![v_{p}[f]=\nabla f(p)\cdot v_{p}=1 v_{p}[f]=\nabla f(p)\cdot v_{p}=1](https://s0.wp.com/latex.php?latex=v_%7Bp%7D%5Bf%5D%3D%5Cnabla+f%28p%29%5Ccdot+v_%7Bp%7D%3D1&bg=FFFFFF&fg=000000&s=0) 。
。
我們發現,由方法一跟方法二得到的結果相同。
歐氏空間中的 維曲面
維曲面
假設(1)
(2)任意的
則我們稱映射
我們使用
範例:令
當你把不同的
定義:令
範例:
光滑流形的一般定義
嚴謹的流形定義如下:假設假設

以下我們談到的
定理: (Whitney Embedding Theorem) 假設
這個定理告訴我們,所有的光滑流形都是某個歐氏空間中的光滑曲面。
光滑流形的環空間定義方式
令定理:函數空間
如果
定義:如果
定理:
假設
換句話說,環空間除了具有拓樸空間的概念外,我們也定義了他上面由環層
任給一個
定理:光滑流形與其上的光滑映射構成了一個範疇。
基本上來說,光滑流形可以視為某一類的環空間 滿足:存在一個
滿足:存在一個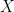 開覆蓋
開覆蓋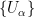 使得對任意的
使得對任意的 ,環空間
,環空間 與環空間
與環空間 是同構的。換句話說,光滑流形局部上來說,他跟歐氏空間一樣,他上面的函數空間跟歐氏空間上的光滑函數所形成的空間也是一樣的(在同構意義下)。換句話說呢,如果給一個
是同構的。換句話說,光滑流形局部上來說,他跟歐氏空間一樣,他上面的函數空間跟歐氏空間上的光滑函數所形成的空間也是一樣的(在同構意義下)。換句話說呢,如果給一個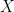 上的可微分函數,我們取局部座標系
上的可微分函數,我們取局部座標系 那麼
那麼 就可以寫成歐氏空間中的可微分函數
就可以寫成歐氏空間中的可微分函數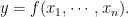 這樣的對應關係
這樣的對應關係
是一個代數上的同構關係。不僅如此,透過這樣的代數關係,我們把歐氏空間中的微積分學就這樣的搬到了光滑流形上。局部上來說,由於光滑流形看起來就是歐氏空間,流形上的光滑函數就是歐氏空間中的光滑函數。你當然希望你的微積分在座標變換下的意義是不變的,因此,你會要求你的函子 是一個層。基本上來說,層的概念就是透過微分流形才產生的。而層的一些條件就是在告訴你,微分流形上的微積分學是良定(well-defined)的(在座標變換的意義下不變)。從現在開始,你知道的微分流形的概念,把古典微積分學套入,你就可以開始研究微分幾何。
是一個層。基本上來說,層的概念就是透過微分流形才產生的。而層的一些條件就是在告訴你,微分流形上的微積分學是良定(well-defined)的(在座標變換的意義下不變)。從現在開始,你知道的微分流形的概念,把古典微積分學套入,你就可以開始研究微分幾何。
%d 位部落客按了讚:
的manifold是不是要Housdorff該定理才會對?(因為這裡的mainfold好像沒有特別說是Housdorff)
——
thanks for your this post with picture, very good, and I have to read it again, but I like it a lot. I understand 微分算子 as 拉普拉斯算子, what is 齐次算子 as quoted in the above wiki? a good article:物理激发的数学 – 中国科学院数学研究所www.math.ac.cn/index_E/post/…/PPT110907.pdf
形的A- 亏格恰好是黎曼流形上狄拉克算子. 的指标。 几何分析中许多有效的方法都是受物理学家. 启发的如. 启发的如平均曲率流是物上首先. 平均曲率流是物上首先 …
you have three dark areas:
1 in the top: dark area=overlap of 開覆蓋 Ua and 開覆蓋 Ub?
2. this " overlap" is 微分同胚 of Rn’s two dark areas, in the lower part of the picture, which is 一個拓樸流形 X?
http://www.dimensions-math.org/, you know that site, I think, a very good one
1. the bottom 2 dark areas: 2 Rn space, or “local coordinate system"
the left one: lines more like x horizontal type (of 2d coordinate system, x horizontal, y vertial);
the right one: lines more like y vertial type,
individually
2
together, they (bottom 2 dark areas) have to “work out" “a common gauge or measure system" as in the darked area in the top (流形)?
共形几何就是研究保角变换群下的不变量. 它介乎于拓扑和黎曼几何之间"共形映射就是保角映射, 如图1所示. 在无穷小邻域, 共形映射就是放缩变换. 它保持局部形状, 比如它将无穷小圆周映成无穷小圆周. 如图2所示, 这个bunny 曲面通过一个共形映射映到平面. 如果平面有一个circle packing, 则通过拉回得到bunny 曲面上的一个circle packing. 如果给平面铺上棋盘格, 则同样得到bunny 曲面的棋盘格修饰, 其中直角和正方形都是保持的.曲面上的两个黎曼度量是共形的, 如果它们定义的角度是相同的. 共形结构就是指曲面上度量的共形等价类, 而黎曼曲面就是带有共形结构的光滑曲面. 因此在黎曼面上, 我们可以度量角度, 但不能度量长度. 每一个带有度量的曲面都自动成为一个黎曼曲
面。如果两个黎曼曲面之间存在共形映射, 则称它们是共形等价的. 显然, 共形等价是黎曼曲面间的一个自然的等价关系. 共形几何的目的就是在共形等价意义下对黎曼曲面进行分类, 这就是所谓的模空间问题. 给定一张光滑曲面, 考察它上面的所有共形结构在共形等价下的模, 这个集合被称为曲面的模空间. 对于具有正亏格的封闭曲面, 模空间是正维数的有限维空间."
yes, thanks
also: http://www.dimensions-math.org/, you know that site, I think, a very good one
if you could read their chapter 7,8,9 about 流形, very short writings, and tell me your comments, if you could, thanks
http://www.dimensions-math.org/, chapter 7,8,9 about 流形"
I think those chapters have “在複的解析函數的作用下,幾何圖形的夾角會被保持" in their graphic presentation, 複函數 is critical to understand 流形 with high dimensions,
they are very good conceptual and graphic presentations, but without " math" part, where do I find the math part, in your blog? do you have a table of contents?
thanks
———-
“[PDF]
REAL AND COMPLEX SMOOTH MANIFOLDS
http://www.math.psu.edu/katok_a/TOPOLOGY/Chapter4.pdf
File Format: PDF/Adobe Acrobat – Quick View
In this course, we do not go deeply into the theory of complex manifolds, limiting our study to some illustrative examples. EXAMPLE 4.9.1. The Riemann sphere …
“
————
now, question:
“该曲面的形状是任意的,只有该曲面的边界具有物理意义"
曲面的边界," =local “切空间 余切空间
where
"
1、切空间就是逆变基矢张成的空间,余切空间就是协变基矢张成的空间。
2、各逆变基矢之间的关系(投影)是逆变度量系数,各协变基矢之间的关系(投影)是协变度量系数。(统称为度规。)
3、逆变矢量与协变矢量可做对偶内积(对偶投影)。 逆变基矢与协变基矢的关系是对偶内积(投影)为δ. (克罗内克尔符号。附标相同时为1,附标不同时为0).
4、投影为0,可图示为正交;否则示为斜交。
"
http://www.fxkz.net/forum.php?mod=viewthread&tid=7120
graphically:
“一个矩阵的行列式就是一个平行多面体的(定向的)体积,这个多面体的每条边就对应矩阵的列"
phymath999: phymath01 一个矩阵的行列式就是一个平行多面体的 …
phymath999.blogspot.com/…/phymath01-jacobi.html – 轉為繁體網頁
2013年2月28日 – phymath01 一个矩阵的行列式就是一个平行多面体的(定向的)体积,这个多面体的每条边就对应矩阵的列。如果学生们得知了这个秘密(在纯粹的 …
my question:I hope I am not too much off, in terms of basic conceptual understanding of those basic but critical concepts?
这个规范场为某个曲面上的δ函数,该曲面的形状是任意的,只有该曲面的边界具有物理意义,理论在曲面形变下的不变性可看作是一种新的规范对称性。
——
这个规范场为某个曲面上的δ函数,该曲面的形状是任意的,只有该曲面的边界具有物理意义,理论在曲面形变下的不变性可看作是一种新的规范对称性
I will think about your answer about “你的問題問反了" “把電磁場看成是某種規範的曲率", I like wely, and remember Einstein’s comment on this.
here is another article, a good one, but kind of difficult for me to read, in terms of math, and I hope some day you can write an “easier" one
[PDF]
规范场与主纤维丛上的联络*
wulixb.iphy.ac.cn/EN/…/downloadArticleFile.do?…id… – 轉為繁體網頁
檔案類型: PDF/Adobe Acrobat – 快速檢視
由 KH LOOK 著作 – 2005 – 相關文章
本文较详细地给出物理上的规范场与数学上的主纤维丛上的联络论之间的对应关系, 从. 而以联络论的观点 … 作为切向量丛的一截面(Scction). 然后我们指出薰一般的 …
作为切向量丛的一截面(Scction):规范场
截面曲率:规范场强,
“當一個多面體在空間中運動,遇到蜥蜴的平面時,多面體與平面的截面是個多邊形。當多面體運動,多邊形變形,當 多面體穿過平面時它最終消失 (假設多面體能穿過平面,就像 Marcel Aymé 的「穿牆術」!)。蜥蜴只看見動態變化的多邊形:關注他們如何變形。通過一點經驗他們(也許)能最終對多面體有個直覺的感受,即使他們不能在空間中看到多 面體。"
for most of us whose logic and sense are based on our local living experiences, very often at a single point of a 平面:
1) measuring “動態變化的多邊形" is difficult, we often only see part of 多邊形.
2) measuring 截面(“曲面不一定是超曲面")曲率: even more difficult
3) even we did 1) and 2) well, we may have a group of 偏微分方程 like 爱因斯坦方程, which will give us some ideans about 规范场 (as represented by Marcel Aymé in the above “background " or analogy )
4)数值解 of “爱因斯坦方程" already difficult, not to mention 解析解
I’m an application person;the following folks are professional, like you; “sage" , one of the folks in the following forum, works and teaches in 普林斯頓 Univ, if I remember “http://www.fxkz.net/forum.php?mod=viewthread&action=printable&tid=6062″
第23 卷第4 期物学voL 23, No. 4. 1974 年7 月AcTA PHYSICA SINIcA July, 1974. 规范场与主纤维丛上的联络*. (中国科学院数学研究所). 提要. 本文较详细地给出。有关规范场与纤维丛关系问题的三次阐释。和现代微分几何中的纤维丛理论有关,并让杨振宁. 去读斯廷罗 … 一研究结果“不可积相因子和规范场的整体表. 示”[5] 。 … 和曲率张量局部坐标变换公式(1. 8): F′a … 规范势Bμ. 主纤维丛上的联络Γa μ. 场强Fμv. 曲率张量Fa μv。规范场的变换。曲率张量
幾何,弦論與量子環的不便性/王金龍 – 中大校訊
sec.ncu.edu.tw/ncunews/166/invited_101.html
最著名者如費因曼的路徑積分,這個理論必須在無窮維度的路徑空間中進行積分。 …. 這些向量空間以及其相關的Dolbeault上同調群構成了這個量子理論的希爾伯特 …
this is your area, I guess.
同調群, what a beautiful concept, many apps will come out of it
“將積分化簡為有限維度模空間上的問題" 模空間 to help provide qm, qft, etc with a solid math logic foundation
yes, I will read it.
this young Chinese graduate student did a great job in “picturing" it for me, I copied a few his post in the below.
http://topologyandgeometry.blogspot.com/
now, with AI and computer graphics advancing rapidly everyday, differential geometry etc will pick up by many people with apps coming out of it in many areas