"黎曼度量的实质是在流形每一点的切空间定义了一个内积.
它在整个切丛上没有意义. "
第一基本形式- 维基百科,自由的百科全书
在微分几何中,第一基本形式(first fundamental form)是三维欧几里得空间中一个曲面
微分几何中,黎曼几何研究具有黎曼度量的光滑流形,即流形切空间上二次形式的选择。它特别关注于角度、弧线长度及体积。把每个微小部分加起来而得出整体的数量。
黎曼认识到度量只是加到流形上的一种结构,并且在同一流形上可以有许多不同的度量。黎曼以前的数学家仅知道三维欧几里得空间E3中的曲面S上存在诱导度量ds2=Edu2+2Fdudv+Gdv2,即第一基本形式,而并未认识到S还可以有独立于三维欧几里得几何赋予的度量结构。黎曼意识到区分诱导度量和独立的黎曼度量的重要性,从而摆脱了经典微分几何曲面论中局限于诱导度量的束缚
黎曼认识到度量只是加到流形上的一种结构,并且在同一流形上可以有许多不同的度量。黎曼以前的数学家仅知道三维欧几里得空间E3中的曲面S上存在诱导度量ds2=Edu2+2Fdudv+Gdv2,即第一基本形式,而并未认识到S还可以有独立于三维欧几里得几何赋予的度量结构。黎曼意识到区分诱导度量和独立的黎曼度量的重要性,从而摆脱了经典微分几何曲面论中局限于诱导度量的束缚
第一基本形式,
在微分几何中,第一基本形式(first fundamental form)是三维欧几里得空间中一个曲面的切空间中内积,由 R3 中标准点积诱导。它使得曲面的曲率和度量性质(比如长度与面积)可与环绕空间一致地计算。
高斯曲率[编辑]
一个曲面的高斯曲率由高斯的绝妙定理断言一个曲面的高斯曲率可以只用第一基本形式及其导数表示,从而 K 事实上是曲面的一个内蕴不变量。高斯曲率用第一基本形式明确的表达式由 Brioschi 公式给出。
第二基本形式[编辑]
维基百科,自由的百科全书
微分几何中,第二基本形式(second fundamental form)是三维欧几里得空间中一个光滑曲面的切丛上一个二次形式,通常记作 II。与第一基本形式一起,他们可定义曲面的外部不变量,主曲率。更一般地,若在黎曼流形中一个光滑超曲面上选取了一个光滑单位法向量场,则可定义这样一个二形式。
在参数 (u1, u2)-曲面给定点处系数 bα,β 由 r 的二次偏导数到 S 的法线的投影给出,利用点积可写成:
 是高斯映射,而
是高斯映射,而 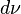 是
是  的微分视为一个向量值微分形式,括号表示欧几里得空间的度量张量。
的微分视为一个向量值微分形式,括号表示欧几里得空间的度量张量。
更一般地,在一个黎曼流形上,第二基本形式是描述一个超曲面形算子(记作 S)的等价方法,
 表示周围空间的共变导数,n 超曲面上一个法向量场。如果仿射联络是无挠的,则第二基本形式是对称的。
表示周围空间的共变导数,n 超曲面上一个法向量场。如果仿射联络是无挠的,则第二基本形式是对称的。
第二基本形式的符号取决于 n 的方向的选取。(这称为曲面的余定向,对欧几里得空间中的曲面,等价于给定曲面的一个定向)。
 表示共变导数
表示共变导数  到法丛的正交投影。
到法丛的正交投影。
在欧几里得空间中,子流形的曲率张量可以描述为下列公式:
对一般的黎曼流形必须添加周围空间的曲率;如果 N 是嵌入黎曼流形 (M,g) 中一个流形,则 N 在诱导度量下的曲率张量 可以用第二基本形式与 M 的曲率张量
可以用第二基本形式与 M 的曲率张量  表示出来:
表示出来:
R3 中曲面[编辑]
引论[编辑]
R3 中一个参数曲面 S 的第二基本形式由高斯引入。最先假设曲面是两次连续可微函数的像,z = f(x,y),且平面 z = 0 与曲面在原点相切。则 f 以及关于 x 和 y 的偏导数在 (0,0) 皆为零。从而 f 在 (0,0) 处的泰勒展开以二次项开始: 高阶项,
高阶项,
经典记号[编辑]
一个一般参数曲面的第二基本形式定义如下。设 r=r(u,v) 是 R3 中一个正则参数曲面,这里 r 是两个变量的光滑向量值函数。通常记 r 关于 u 和 v 的偏导数为 ru 与 rv。参数化的正则性意味着 ru 与 rv 对 r 的定义域中任何 (u,v) 是线性无关的。等价地,叉积 ru × rv 是曲面的一个非零法向量。参数化这样就定义了一个单位法向量场 n:现代记法[编辑]
一个通常曲面 S 的第二基本形式定义如下:设 r=r(u1,u2) 是 R3 中一个正则参数曲面,这里 r 是两个变量的光滑向量值函数。通常记 r 关于 uα 的偏导数为 rα,α = 1,2。参数化的正则性意味着 r1 与 r2 在 r 的定义域上是线性无关的,从而在每一点张成 S 的切空间。等价地,叉积 r1 × r2 是曲面的一个非零法向量。这样参数化定义了一个单位法向量场 n:在参数 (u1, u2)-曲面给定点处系数 bα,β 由 r 的二次偏导数到 S 的法线的投影给出,利用点积可写成:
黎曼流形中的超曲面[编辑]
在欧几里得空间中,第二基本形式由 是高斯映射,而
是高斯映射,而 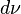 是
是  的微分视为一个向量值微分形式,括号表示欧几里得空间的度量张量。
的微分视为一个向量值微分形式,括号表示欧几里得空间的度量张量。更一般地,在一个黎曼流形上,第二基本形式是描述一个超曲面形算子(记作 S)的等价方法,
 表示周围空间的共变导数,n 超曲面上一个法向量场。如果仿射联络是无挠的,则第二基本形式是对称的。
表示周围空间的共变导数,n 超曲面上一个法向量场。如果仿射联络是无挠的,则第二基本形式是对称的。第二基本形式的符号取决于 n 的方向的选取。(这称为曲面的余定向,对欧几里得空间中的曲面,等价于给定曲面的一个定向)。
推广为任意余维数[编辑]
第二基本形式可以推广到任意余维数。在这种情形下,它是切空间上取值于法丛的一个二次型,可以定义为 表示共变导数
表示共变导数  到法丛的正交投影。
到法丛的正交投影。在欧几里得空间中,子流形的曲率张量可以描述为下列公式:
对一般的黎曼流形必须添加周围空间的曲率;如果 N 是嵌入黎曼流形 (M,g) 中一个流形,则 N 在诱导度量下的曲率张量
 可以用第二基本形式与 M 的曲率张量
可以用第二基本形式与 M 的曲率张量  表示出来:
表示出来:| 季候风 发表文章数: 262 内力值: 310/310 贡献度: 3398 人气: 154         |
当我们谈论一个流形, 总是假定它已经是一个拓扑空间. 其它添加的结构必须与这个预先存在的拓扑相容.
如果要谈黎曼流形, 首先要在流形上加一个微分结构, 它与原来拓扑的相容性没有问题 --- 微分结构的定义本身依赖于预先存在的拓扑; 然后再指定一个二阶正定对称光滑张量场 g; 黎曼度量 g 的一个重要作用是可以用来定义流形上曲线的长度, 这样两点之间的距离可以定义连接两点所有曲线长度的下确界, 这样就在流形的底集合上定义了一个 "距离"; 集合上的任一距离会诱导一个拓扑, 但是在黎曼流形上早就预先设定了一个拓扑, 所以如果这个有黎曼度量定义出来的距离诱导的拓扑最好与原来设定的拓扑是同一个拓扑, 所以标准的黎曼几何教材上都会就这个问题进行讨论, 而事实上新拓扑的确就是旧拓扑. 这样我们在谈论黎曼流形的时候, 连续性就没有任何歧义: 既可以用局部坐标来表达连续性, 又可以用距离来表达连续性. 在英文里, 赋予了 "距离" 的集合传统上叫做 "metric space", 这个距离传统上也叫 metric. 但是近些年由于黎曼几何在数学各个分支的渗透, 它越来越成为更基础的课程. 这样为了避免初学者混淆概念, 很多新写的教材上把原来的 "metric space" 的 "metric" 称为 "distance". 中文就更方便了, 即便把 "度量空间" 改叫做 "距离空间" 也颇为顺口. 为了强调 g 这个 "metric" 跟距离的不同, 一般都会强调说这是一个 "Riemannian metric" 而不仅仅简单叫它 "metric". 近几十年经过 Gromov 等人的工作, 很多原来在黎曼流形上研究的对象, 工具和问题, 现在已经成功地移植到了性质比较接近黎曼流形的距离空间.
| ||
| 季候风 发表文章数: 262 内力值: 310/310 贡献度: 3398 人气: 154         |
更正: 上一贴第三行 "定义" 应该是 "定义为"
| ||
| 枭雄 发表文章数: 6 内力值: 74/74 贡献度: 36 人气: 28  |
非常感谢各位前辈的指导!由于非钻研数学之人,所以对某些概念的理解比较肤浅!
因为有界只对度量空间有意义,在拓扑学的教材里,只是说度量可以自然地诱导出拓扑,而一般拓扑空间的拓扑结构并非都可以由度量诱导而来。 实际上我遇到的问题是紧致黎曼流形的有界性,现在按照我对各位前辈之言的理解,说紧致黎曼流形有界应该没有问题吧! 当然还有个地方觉得比较神奇,不知我的理解对否: 黎曼流形M,某点x处的切空间TxM,切空间集合TM。按照各位前辈的说法,黎曼度量是定义在TM上,却可以用来定义M上两点之间的距离!而如果把这个距离说成是M上的一个度量,那这个度量和黎曼度量不是一回事!
| ||
| 季候风 发表文章数: 262 内力值: 310/310 贡献度: 3398 人气: 154         |
黎曼度量的实质是在流形每一点的切空间定义了一个内积.
它在整个切丛上没有意义. |













No comments:
Post a Comment