||
曲率曲率说明
表示曲线弯曲程度的量.
平面曲线的曲率就是针对曲线上某个点的切线方向角对弧长的转动率,通过微分来定义,表明曲线偏离直线的程度。曲率越大,表示曲线的弯曲程度越大。
K=lim|Δα/Δs|,Δs趋向于0的时候,定义K就是曲率。
曲率的倒数就是曲率半径。
圆弧的曲率半径,就是以这段圆弧为一个圆的一部分时,所成的圆的半径。 曲率半径越大,圆弧越平缓,曲率半径越小,圆弧越陡。曲率半径的倒数就是曲率。曲率 k = (转过的角度/对应的弧长)。当 角度和弧长同时趋近于0时,就是关于任意形状的光滑曲线的曲率的标准定义。而对于圆,曲率不随位置变化。
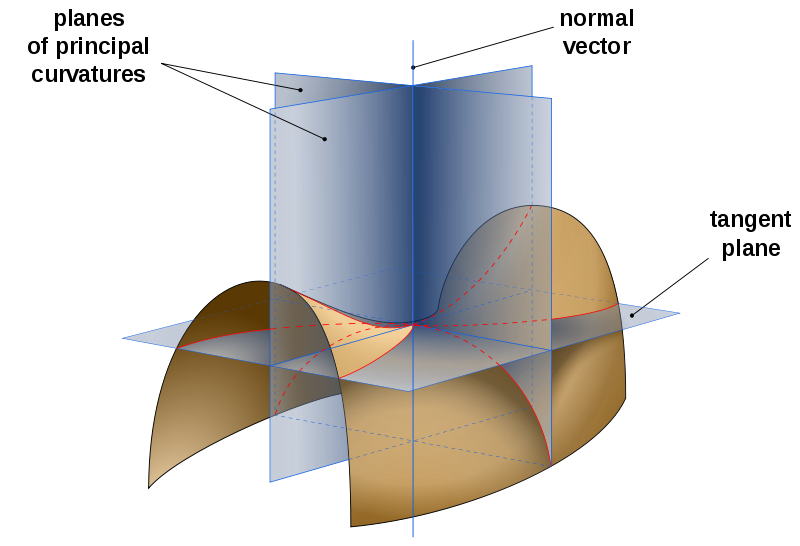
高斯曲率 曲面论中最重要的内蕴几何量。设曲 面在P点处 的两个主曲率为k1,k2,它们的乘积k=k1·k2称为曲面 于该点的总曲率或高斯曲率。它反映了曲面的一股弯曲程度。高斯曲率k的绝对值有明显的几何意义。设Δб是曲面上包含P点的一小片曲面(其面积仍用Δб表示),把Δб上的每点的单位法向量n平移到E3的原点O处,那么n的终点 的轨迹是 以O为中心的单位球面 S2上的一块区域 Δб* 。这个对应称为高斯映射。曲面在P点邻近弯曲程度可用Δб*( 其面积仍用Δб*表示)与Δб的面积比刻画。曲面在P点的 高斯曲率的 绝对值正是这个比值当Δб收缩成P点时的极限。
故事:
古典的几何学者在讨论三维空间中的曲面时,他们留意到曲面上每一点的曲率,都有两个不同的选择。比如在一个圆柱面上,一个方向是沿其横切的圆,另一个则是沿垂直线。
高斯在1827年发现这两个曲率的乘积具有惊人的属性。当我们令曲面在空间变型,只要它没有拉长缩短,这个积是不变的!后世称这个积为高斯曲率。
内蕴几何
高斯把这条定理写入《曲面通论》一书中。他指出必须把曲面的内在性质,即身处曲面内扁小甲虫所经验的属性,与其外在的,即依赖于曲面如何置于空间的性质区分开来,而只有内在性质,才值得“几何学家焚膏继晷,兀兀穷年地上下求索”。后世称研究这些性质的学问为内蕴几何。
高斯曲率决定曲面的内蕴几何
从球面剪取一片曲面,其高斯曲率为正常数。反过来说,局部而言,任何具正常曲率的曲面都可以等距地映射成球面的一部分。
类似地,从双曲曲面剪取的一片,其高斯曲率恒等于―1,而反过来说曲率等于―1的曲面与双面曲面局部相等。双曲曲面曾在讨论欧氏第五公理时论及。
高斯对几何的深思
高斯显然因他的定理兴奋不已。但他并没有认为人们对空间已认识透彻。
高斯:“我愈来愈相信,人类的理性并不能证明或理解几何的必要性。也许后世能对空间的本质有新的洞见,但目前这却是不可能的事。”
定义:
曲面论中最重要的内蕴几何量。设曲 面在P点处的两个主曲率为k1,k2,它们的乘积k=k1·k2称为曲面于该点的总曲率或高斯曲率。它反映了曲面的一股弯曲程度。高斯曲率k的绝对值有明显的几何意义。设Δб是曲面上包含P点的一小片曲面(其面积仍用Δб表示),把Δб上的每点的单位法向量n平移到E3的原点O处,那么n的终点的轨迹是以O为中心的单位球面 S2上的一块区域 Δб* 。这个对应称为高斯映射。曲面在P点邻近弯曲程度可用Δб*( 其面积仍用Δб*表示)与Δб的面积比刻画。曲面在P点的 高斯曲率的 绝对值正是这个比值当Δб收缩成P点时的极限。亦即
高斯曲率的符号则指明曲面弯曲的朝向。
知乎:作为交易员参与到 2015 年的救市活动是一种怎样的体验?
比如券商自营和汇金估计都要买买买蓝筹股之类的了……想了解下大家的状态都是怎样的。
本题希望能看到券商自营或者其他机构(公募基金等)的交易员來回答,私募或者一些散户就算啦,关注就好。
—
(感谢大家点赞,但是求关注求荐股就算了。本人在知乎上也有几千粉,平日答的许多都是游戏领域的内容)
利益相关,本人是参加这次救火行动的某券商交易员。
交易员这个行当,其实也只是听指令下单的机构螺丝钉而已,没有太大的能量。今天上头多拆借的五个多亿的资金用于救火,来自上面的大领导的指令,至于我们经理乐不乐意救市,那当然不乐意,因为我们自营部正是前段时间的空头,抛售大量股票,这回证监会约谈各领导,明摆着是让我们再跳进火坑。我们经理认为,暴跌是可以救回来的,牛市是救不回来的,那些大量的被套盘会在第二个顶部极其敏感,很容易解套就跑,形成著名的双顶K线。所以说,出于自身利益考虑,我们是比较气馁的。在券商自营有相当多的工资来自年终津贴,业绩差了钱就得少,都是这个样子。
我们在早盘集合竞价时买入大笔ETF和蓝筹股,标的和数目就不说了。在我打单子的时候是觉得这样很蠢的,早上开高有什么用?K线不好看不说,这就是把我们的钱拿去扔水里。果不其然大量个股从封涨停开始回落,而老总的意思是坚决不补,同时卖掉了一定港沪通的股票。至于尾市拉升,那是嫡系部队干的事情,我们是不会干的。
关于护盘,我们主要在一些重仓的中小盘工业股上有较大的力量。常用的手法包括关键价位阻吓,在低位挂上数百万股的买盘,让空方在抛压前先考虑一下值不值得啃硬骨头;此外就是突然拉升,代价小成效高。不过说实在话我们前期也没怎么护盘,所谓倾巢之下岂有完卵。
PS:关于神秘空头势力,我们公司内部也有不少讨论,但无论是外国投行还是国内保守派,想要引起这么大规模的股市下跌,一定是在牛市早期有大量的盈利盘,这样从沽空期货与砸现货才有那么大的底气与实力。从去年七月以来,大量基金盈利在100%到300%间,就算把股市砸到3000点,他们也不会亏损的。我上知乎总有一种错觉,那些在牛市前期资产翻了数倍的盈利者还少吗?之所以许多人叫得欢,实际上只是因为贪罢了。
PS2:知乎上有人说根本没有空头势力,以及各种骂散户骂股评家骂政府,我觉得他们其实是躺枪。问我信不信阴谋论,我没证据不好答,但是说这是市场调整,那我是坚决不信的。
很显然,经济学理论里面有一条定理,大家每个人都是理性和自利的。想想如果你是空头,你会怎么做?政府出那么多利好,明显应该顺水推舟,买入筹码,然后高位出货,让之前观望以为底部到了的股民街盘。但是最近这段时间,政府出一个利好就收一次大阴线,放到全世界的股市历史上都太罕见了,我们投资经理都骂娘,谁TM既断自己财路还断别人的?你觉得点位高了,逐步出货就是,唯恐天下不乱,实在让人无法理解。更别说前几天期指上的惊人异动了,大家都是体制内的人,我咋没听说有券商衍生品交易部在出利好后用天量的钱做空呢?这是疯了吗?
—
我是一个私募交易员,我每天盯盘,自行操盘,我不参与救市,我的工作是发现获利机会。行情一路走过来我也看明白了一些事情,前来抛砖引玉。
“救市”的两种定义
散户之所以对目前的行情感到绝望,完全是因为被政府“救市”两字欺骗了,行情走到今天,不难观察到,国家队所谓的救市:是减缓市场下跌的速度,防范系统性金融风险。典型散户期望的救市:是手上股票解套,甚至V形反转,剑指一万点,从结果来看国家队并无此意愿(或力所不能及)。回顾最近10个工作日,每次政策利好,都是怕你跑,因为要让融资盘先跑、银行理财产品先跑,受利好政策影响去抢反弹的人,他们得偿所愿”为国接盘”了,整个下跌速度被略微放缓了,然而,跌得还是太快了,券商和银行的资金还是没来得及跑光,于是有了操真金白银的国家队亲自介入。各种政策,文件,喊话,就是让大家不要绝望,抛盘不要那么大,抛得不要那么急,无奈囚徒困境出现,今天你不跑,就没有跑的机会了,到了明天就是-10%,所以只能一起往下杀。
化解融资盘
众所周知目前这个点位场外配资已经差不多清光,主要的系统性风险来自融资盘,2w亿的融资盘如果踩踏出逃,会影响券商和银行的正常经营(主要是巨额坏账),甚至波及实体经济,那么我们看看融资余额最大的股票是那几只?
如果你去翻一下融资“重灾区”,很少有封死跌停的,他们的流动性得到了保证,谁在提供买盘呢?是国家队,包括跌停扫货,拉权重涨停稳定指数,看上去很暴力,很无脑,对小票于事无补,对人气于事无补,换个方式想,小票这么多,拉哪个?拉哪个也解决不了融资盘这个定时炸弹,虽然能提升人气,但是盘子小,一拉就吃进5%,要举牌了,变成了大股东,这不现实。别忘了,让融资盘变现,市场也就有了更多抄底资金。
小票怎么办
小票没有国家队关照,每天无量跌停,典型的踩踏式出逃+恐慌情绪,没人敢做多抢反弹,以现在的市场情绪,回购、增持、员工持股,这种级别的利好再多也没用。手上有股票,从4、5千点拿下来的,只能祝你好运。但是不要忘记,波动越大,机会也就越大,如果你还有子弹,千年难遇的发财机会就集中在这些被打压的一塌糊涂的品种里,捡便宜筹码的时机到了,甚至几天里赚30%都不是梦,请自行研究。
期指
我唯一没想通的是国家队在期指上的战略,为什么要限制开空仓,难道就是为了迎合民间的“敌对势力论”?转移矛盾的结果是逼得本来用期指套保机构去砸现货,制造出更恐慌的情绪,不利于减缓下跌速度。盘中的战术也不明确,今天(7月8日)早盘IF IC几乎开在跌停,强行翻红,但是死守策略又不延续,IF在3500点有几次挣扎,最终却还是封死跌停,毫无流动性,莫非是今天的“救市额度”用光了?期指封跌停的负面效应是现货也放弃了挣扎……明天下一个台阶是大概率事件,在平仓线附近退守是很危险的。
有感而发,随便写写。写的不对,欢迎交流。
—
谢邀,体验一般般,上面吩咐,下面照做。
比平时开会多,资金量突然增大了,基本就这两点变化吧。
然后在知乎看到各路股神的意淫,这次的救市各种被抨击,感觉好搞笑。
真当我们是解放军了,以为中金社保出钱,再坑一下券商公募,就是来给你们解套的呗?
制定这次救市计划的人比你们牛逼多了。
最后多说一句,这些天一直有人在偷偷吃货,捡便宜筹码,估计是有意高抛低吸吧。
中午吃饭的时候问同事:“知乎的喷子怎么这么多?以前质量没这么差啊。”
“艹,你看咱们这里谁傻逼呵呵的玩儿知乎?哪句话出问题就进去了。再者说,人家赔了钱,没杀人没放火,骂两句娘总行吧?谁让你凑上去找骂嘞。”
最后一句好有道理,我彻底原谅了这些喷子,也终于明白为什么现在知乎越做越差了。
—
不请自来,虽然不是题主要问的人群,但是在私募玩高频,忍不住手痒冒昧答一记。
——以下正文——
六月初我们的量化对冲产品就加上了期指空仓,大概10号左右基本覆盖掉全部现货。然后…每天盼着调整。
当时策略会讨论的结果是这次回调到4000点,没想到会以这么暴力的手段回调,而且幅度之深,速度之快,已经无法定义为调整了。上周我们就预计到周末会有密集的政策出台,在周五之前平掉了期指空头,全仓杀入蓝筹股。
周末果然出了王炸,我们整个周末都是处在一片欢乐祥和的气氛中。朋友圈也开始吹逼,加入护国保卫战,誓将空头一网打尽。
这种气氛一直持续到周一收盘,当时有一种即将走上人生巅峰的感觉。然后,周二开盘就懵逼了,什么鬼?!重仓股全线跌停。等到周三我们想加上套保,已经被限制开仓了!
为国护盘成了为国接盘,我想现在很多机构都是同样的赶脚。缺乏确定性,是我们最厌恶的事情,机构尚且如此,散户惨状不必多言。我在券商的朋友,现在都忙着解决股票质押和双融的强平呢,谁还有心思去救大盘,券商营业部则是加上防盗网,准备救心丸,人人自危,又如何拯救?
现在是最坏的时候吗?我觉得还有更坏的在前面等着。熬不过去,也许再也没有翻身的可能。神仙打架,我们凡人找个角落趴好装死吧。
—
谢邀。
我不属于公募或券商自营以及国家队的交易员,无从谈体验。〈注:以下交易员专指,公募或券商自营以及国家队的交易员〉
只能谈谈对于他们操盘手法的看法。先总结:他们这次是把交易员仅存的一丝尊严与颜面也丢光了。
晚上抽空细说。
好。我们来谈谈。
是次救市对错与否先放一边,监管部门之前的昏招叠出亦放一边,之前之种种都与交易员无关,而本次救市最大之动作是从周末的紧急会议开始,有两点措施是最为有力的:
①券商在及其不情愿下被要求出资合计1200亿。
②央行为证金公司提供未具额度流动性。
至此交易员们将要登上舞台了,其“光荣与梦想也即将被见证”。
何为救市关键?自然是砸下资金,以求稳定市场信心。可以说在周一开盘前资金—―这一救市最关键之要素已具备,接下来就是打法。
回到正题。
为什么说:“他们这次是把交易员仅存的一丝尊严与颜面也丢光了。”
在占尽信息优势、资金优势甚至道德优势的情况下,在错误的时间、错误的地点、用错误的手段打了一场惨不忍睹、颜面尽失的不对称败仗。
分别来说:
①错误的时间,竟然于集合竞价时段动用宝贵的资金,大量挂涨停价封住个股,甚至IC500期指都一度封于涨停。到底是谁下的如此愚不可及的命令。用如此自杀式手法,无异于摇旗号召大家来做空IC。
②错误的地点,如果说早盘封停IC做法,是妄图迅速解决战斗,赚尽眼球,强力挽回市场信心,还有情可原。那下午专注硬拉IH50系列,何止是愚蠢简直就是荒诞。敢情半天了都没弄清楚市场信心源于何处。IH你不动它都不会崩跌太多,而关键是IC500系列啊,这才是信心之源,稳住IC恢复流动其流动性,让大量要出来的资金轻松撤离,自然而然也就止住了整个大盘崩跌之势。因为IC是影响了市场广泛的参与者,特别是大量机构与私募及融资盘,这些资金顺利撤离,被动做空也就无从谈起。而浪费资金在IH50能一时稳住上证,也不可能持续在IC暴跌情况下独善其身。
③错误的手段,以历来各国、各地区救市之经验来看,你不能指望在股市以成崩溃之势时,意图迅速扭转趋势,力挽信心缺失狂澜。如早盘的打涨停板,与下午的硬拉,这都是无故浪费宝贵救市资金之举,高开低走下来反而更会造成隔天恐慌性大规模抛盘。正确的做法是,开源引流,有充裕的救市资金,而不硬拉,只稳住盘面震荡或缓跌即可,让风险缓释,而我们可爱的交易员门却急于完成任务或造就市场奇观,一会儿淹死一会儿渴死,如此如何挽回市场信心,不造成更大恐慌已是万幸,哪怕市场本来有得救,也被如此手法给结果了。
券商自营与公募交易员其尊严在于,每个交易员所在团体本来都有独立、自由决策交易之权力;虽然公募往往在意业内排名,不重视绝对收益,而券商自营不论规模大小,均为自家核心力量一部。国家队交易员之尊严在于,汇金、证金都作为国家意志稳定市场之力量存在,而自豪感油然而生,虽然是投入之资金往往效率奇低。而是次救市券商自营与公募独立、自由决策交易之权力被无情剥夺;国家队交易员作为稳定市场之力量而无能为力,反而造就更为剧烈的波动与恐慌。因而他们仅存的一丝尊严与颜面也丢光了。
待补充……..
黎曼zeta 黎曼球可以看作复数平面上缠一个球体 锥面上顶点处的曲率等于无穷大("频谱分析"),其余点的曲率为0; 從雙曲曲面剪取的一片,其高斯曲率恒等於負一, 反過來說曲率等於負一的曲面與雙面曲面局部相等

一个几何球体上的两个方位线之间的区域。
图片来源:KARTHIK Narayanaswami
The region between two
Image credit: Karthik Narayanaswami

![黎曼球面Riemann <wbr>sphere对冲基金数学模型方法]()
黎曼球可以看作复数平面上缠一个球体(通过某种形式的立体投影
布朗,詹姆斯和丘吉尔,鲁埃尔(1989年),
格里菲思,菲利普·哈里斯,约瑟夫(1978年)。
彭罗斯,罗杰
鲁丁,瓦尔特(1987年)。
[
Hazewinkel,米歇尔,编辑。
莫比斯转换揭晓
古典的幾何學者在討論三維空間中的曲面時,他們留意到曲面上每一點的曲率,都有兩個不同的選擇。比如在一個圓柱面上,一個方向是沿其橫切的圓,另一個則是沿垂直線。高斯在1827發現這兩個曲率的乘積具有驚人的屬性。當我們另曲面在空間變型,只要它沒有拉長縮短,這個積是不變的!後世稱這個積為高斯曲率
[PPT]請點選此處下載。
算術基本定理與黎曼zeta函數 送交者: 莊銳 2013年01月12日16:19:17 于 [教育學術] 發送悄悄話
黎曼猜想是什麼(2)
2. 算術基本定理與黎曼zeta函數。
算術基本定理又叫唯一分解定理。這個定理是說,每一個大于1的正整數N都可以寫成有限個質數(或者素數)的乘積;這個乘積叫做N的因數分解。N的因數分解中的質數因子可以有重復但是其個數是由這個被分解的正整數確定的,不同整數的分解是不可能相同的。這個定理幾乎有兩千年的歷史。 算術基本定理描述了全體素數是整個大于一的正整數之集合的生成集;就是說從所有素數的集合出發,把所有有限乘積都加進去就得到了所有大于1的正整數之集合。
描述質數之個數的結論叫做素數定理,這個定理根據估計的準確度可以有多種不同的形式。固定任何一個比一大的正整數N,通過簡單的實驗人類很早就知道在一到N之間我們可以期待有少數質數。比如在1到10之間有2,3,5,7這四個質數;佔幾乎五分之二。 這個比例平均地講隨著N的增加在減少,實驗結果告訴我們在一到N之間大概有 M =log(N) 分之一的整數是質數。這里的 log(N) 是類似與常用對數的(以e為底的)自然對數。這個e是繼圓周率pi之後的第二個重要數學常數。用公式表示,通常把從一到N之間的質數個數表示為 pi(N)。這里的 pi 用的是圓周率的同一個符號,但是不是指那個圓周率常數,而是用來表示質數計數函數。 最簡單的素數定理是說 pi(N) 大致等于N 與 log(N) 的商。 這里的大致必須用數學詞匯準確地描繪。 其他精確的素數定理就要給出對這個函數的更精確描寫加上對誤差的估計。
在黎曼之前,高斯對質數計數函數有一個猜測,那就是用現在叫做 高斯的(logarithmic integral) 對數積分函數 li(N) 來代替上面所提到的N與log(N)之商。高斯對後來叫做黎曼zeta函數的那個數學對象已經有過一些研究。1859年,黎曼在他唯一關于數論的研究論文中引進復數作為變量,從而制造出現在叫做黎曼zeta函數的這個特殊函數。黎曼zeta函數是一個以復數為變量的函數,除了一個奇點以外這個函數在整個復數平面上是解析的。這里用的的“解析”一詞,基本上就是微積分中無窮次可微分的意思。
要解釋什麼是黎曼zeta函數,我們還是從如何計算質數的個數說起。 數學發展到前兩個世紀中間的時候,已經有了非常成熟的無窮個數字相加的工具。 其實幾乎兩千年前就有“一尺之棰,日取其半,萬世不竭”的說法。如果把二分之一,四分之一,八分之一,十六分之一,等等一切,一直加起來,可以想象其和為一。 嚴格地說,這就是現代數學系大學高年級里學到的“無窮級數”。定義黎曼zeta函數就必須要用到“無窮級數”與“解析”的概念,所以至少要到大學數學系接近畢業的學人們才可能真正理解黎曼zeta函數的定義。
這里給出在某個場合本人曾經使用過的一個籠統解釋,那就是黎曼zeta函數其實就是把所有的正整數添加必要的附帶數據後然後巧妙地糅合在一起得到的一個函數。不難想象,有關整數的所有一切都被揉在里面了。 因此可以說,這個函數既展示了宇宙的完美無瑕,又顯現出這個世界的雜亂無章。 對于數學家們的問題就是,如何從這個非常復雜的函數里面找到清晰的數學數據。
既然有無窮個質數存在,我們可以比如用每一個正整數的倒數來相加。事實上,所有正整數的倒數相加起來叫做調和級數。調和級數的和仍然是一個無窮大;而這正是黎曼zeta函數中唯一一個奇點的來源。如果把所有正整數的平方的倒數加起來,那麼得到的結果等于那個圓周率的平方除以6。這樣用來研究質數個數的黎曼zeta函數與圓周率也有著緊密的聯系。事實上,所有的數學理論都是緊密地聯系在一起的。作為開端,黎曼zeta函數被定義為所有正整數的其復數變量次方的和,比如我們必須定義2的pi次方是什麼意義。但是這個定義只對復數變量的實數部分大于一的時候有用,然後就要進行進一步的解析延拓把這個函數對所有復數變量都給予定義。除了在復數變量為一的時候為無窮大以外,其他所有復數變量對應的函數值都是有限的。這就是對于什麼是黎曼zeta函數的一個簡單解釋。
相關鏈接︰
- See more at: http://bbs.creaders.net/education/bbsviewer.php?trd_id=814267&language=big5#sthash.eazLb8In.dpuf
本题希望能看到券商自营或者其他机构(公募基金等)的交易员來回答,私募或者一些散户就算啦,关注就好。
—
(感谢大家点赞,但是求关注求荐股就算了。本人在知乎上也有几千粉,平日答的许多都是游戏领域的内容)
利益相关,本人是参加这次救火行动的某券商交易员。
交易员这个行当,其实也只是听指令下单的机构螺丝钉而已,没有太大的能量。今天上头多拆借的五个多亿的资金用于救火,来自上面的大领导的指令,至于我们经理乐不乐意救市,那当然不乐意,因为我们自营部正是前段时间的空头,抛售大量股票,这回证监会约谈各领导,明摆着是让我们再跳进火坑。我们经理认为,暴跌是可以救回来的,牛市是救不回来的,那些大量的被套盘会在第二个顶部极其敏感,很容易解套就跑,形成著名的双顶K线。所以说,出于自身利益考虑,我们是比较气馁的。在券商自营有相当多的工资来自年终津贴,业绩差了钱就得少,都是这个样子。
我们在早盘集合竞价时买入大笔ETF和蓝筹股,标的和数目就不说了。在我打单子的时候是觉得这样很蠢的,早上开高有什么用?K线不好看不说,这就是把我们的钱拿去扔水里。果不其然大量个股从封涨停开始回落,而老总的意思是坚决不补,同时卖掉了一定港沪通的股票。至于尾市拉升,那是嫡系部队干的事情,我们是不会干的。
关于护盘,我们主要在一些重仓的中小盘工业股上有较大的力量。常用的手法包括关键价位阻吓,在低位挂上数百万股的买盘,让空方在抛压前先考虑一下值不值得啃硬骨头;此外就是突然拉升,代价小成效高。不过说实在话我们前期也没怎么护盘,所谓倾巢之下岂有完卵。
PS:关于神秘空头势力,我们公司内部也有不少讨论,但无论是外国投行还是国内保守派,想要引起这么大规模的股市下跌,一定是在牛市早期有大量的盈利盘,这样从沽空期货与砸现货才有那么大的底气与实力。从去年七月以来,大量基金盈利在100%到300%间,就算把股市砸到3000点,他们也不会亏损的。我上知乎总有一种错觉,那些在牛市前期资产翻了数倍的盈利者还少吗?之所以许多人叫得欢,实际上只是因为贪罢了。
PS2:知乎上有人说根本没有空头势力,以及各种骂散户骂股评家骂政府,我觉得他们其实是躺枪。问我信不信阴谋论,我没证据不好答,但是说这是市场调整,那我是坚决不信的。
很显然,经济学理论里面有一条定理,大家每个人都是理性和自利的。想想如果你是空头,你会怎么做?政府出那么多利好,明显应该顺水推舟,买入筹码,然后高位出货,让之前观望以为底部到了的股民街盘。但是最近这段时间,政府出一个利好就收一次大阴线,放到全世界的股市历史上都太罕见了,我们投资经理都骂娘,谁TM既断自己财路还断别人的?你觉得点位高了,逐步出货就是,唯恐天下不乱,实在让人无法理解。更别说前几天期指上的惊人异动了,大家都是体制内的人,我咋没听说有券商衍生品交易部在出利好后用天量的钱做空呢?这是疯了吗?
—
我是一个私募交易员,我每天盯盘,自行操盘,我不参与救市,我的工作是发现获利机会。行情一路走过来我也看明白了一些事情,前来抛砖引玉。
“救市”的两种定义
散户之所以对目前的行情感到绝望,完全是因为被政府“救市”两字欺骗了,行情走到今天,不难观察到,国家队所谓的救市:是减缓市场下跌的速度,防范系统性金融风险。典型散户期望的救市:是手上股票解套,甚至V形反转,剑指一万点,从结果来看国家队并无此意愿(或力所不能及)。回顾最近10个工作日,每次政策利好,都是怕你跑,因为要让融资盘先跑、银行理财产品先跑,受利好政策影响去抢反弹的人,他们得偿所愿”为国接盘”了,整个下跌速度被略微放缓了,然而,跌得还是太快了,券商和银行的资金还是没来得及跑光,于是有了操真金白银的国家队亲自介入。各种政策,文件,喊话,就是让大家不要绝望,抛盘不要那么大,抛得不要那么急,无奈囚徒困境出现,今天你不跑,就没有跑的机会了,到了明天就是-10%,所以只能一起往下杀。
化解融资盘
众所周知目前这个点位场外配资已经差不多清光,主要的系统性风险来自融资盘,2w亿的融资盘如果踩踏出逃,会影响券商和银行的正常经营(主要是巨额坏账),甚至波及实体经济,那么我们看看融资余额最大的股票是那几只?
如果你去翻一下融资“重灾区”,很少有封死跌停的,他们的流动性得到了保证,谁在提供买盘呢?是国家队,包括跌停扫货,拉权重涨停稳定指数,看上去很暴力,很无脑,对小票于事无补,对人气于事无补,换个方式想,小票这么多,拉哪个?拉哪个也解决不了融资盘这个定时炸弹,虽然能提升人气,但是盘子小,一拉就吃进5%,要举牌了,变成了大股东,这不现实。别忘了,让融资盘变现,市场也就有了更多抄底资金。
小票怎么办
小票没有国家队关照,每天无量跌停,典型的踩踏式出逃+恐慌情绪,没人敢做多抢反弹,以现在的市场情绪,回购、增持、员工持股,这种级别的利好再多也没用。手上有股票,从4、5千点拿下来的,只能祝你好运。但是不要忘记,波动越大,机会也就越大,如果你还有子弹,千年难遇的发财机会就集中在这些被打压的一塌糊涂的品种里,捡便宜筹码的时机到了,甚至几天里赚30%都不是梦,请自行研究。
期指
我唯一没想通的是国家队在期指上的战略,为什么要限制开空仓,难道就是为了迎合民间的“敌对势力论”?转移矛盾的结果是逼得本来用期指套保机构去砸现货,制造出更恐慌的情绪,不利于减缓下跌速度。盘中的战术也不明确,今天(7月8日)早盘IF IC几乎开在跌停,强行翻红,但是死守策略又不延续,IF在3500点有几次挣扎,最终却还是封死跌停,毫无流动性,莫非是今天的“救市额度”用光了?期指封跌停的负面效应是现货也放弃了挣扎……明天下一个台阶是大概率事件,在平仓线附近退守是很危险的。
有感而发,随便写写。写的不对,欢迎交流。
—
谢邀,体验一般般,上面吩咐,下面照做。
比平时开会多,资金量突然增大了,基本就这两点变化吧。
然后在知乎看到各路股神的意淫,这次的救市各种被抨击,感觉好搞笑。
真当我们是解放军了,以为中金社保出钱,再坑一下券商公募,就是来给你们解套的呗?
制定这次救市计划的人比你们牛逼多了。
最后多说一句,这些天一直有人在偷偷吃货,捡便宜筹码,估计是有意高抛低吸吧。
中午吃饭的时候问同事:“知乎的喷子怎么这么多?以前质量没这么差啊。”
“艹,你看咱们这里谁傻逼呵呵的玩儿知乎?哪句话出问题就进去了。再者说,人家赔了钱,没杀人没放火,骂两句娘总行吧?谁让你凑上去找骂嘞。”
最后一句好有道理,我彻底原谅了这些喷子,也终于明白为什么现在知乎越做越差了。
—
不请自来,虽然不是题主要问的人群,但是在私募玩高频,忍不住手痒冒昧答一记。
——以下正文——
六月初我们的量化对冲产品就加上了期指空仓,大概10号左右基本覆盖掉全部现货。然后…每天盼着调整。
当时策略会讨论的结果是这次回调到4000点,没想到会以这么暴力的手段回调,而且幅度之深,速度之快,已经无法定义为调整了。上周我们就预计到周末会有密集的政策出台,在周五之前平掉了期指空头,全仓杀入蓝筹股。
周末果然出了王炸,我们整个周末都是处在一片欢乐祥和的气氛中。朋友圈也开始吹逼,加入护国保卫战,誓将空头一网打尽。
这种气氛一直持续到周一收盘,当时有一种即将走上人生巅峰的感觉。然后,周二开盘就懵逼了,什么鬼?!重仓股全线跌停。等到周三我们想加上套保,已经被限制开仓了!
为国护盘成了为国接盘,我想现在很多机构都是同样的赶脚。缺乏确定性,是我们最厌恶的事情,机构尚且如此,散户惨状不必多言。我在券商的朋友,现在都忙着解决股票质押和双融的强平呢,谁还有心思去救大盘,券商营业部则是加上防盗网,准备救心丸,人人自危,又如何拯救?
现在是最坏的时候吗?我觉得还有更坏的在前面等着。熬不过去,也许再也没有翻身的可能。神仙打架,我们凡人找个角落趴好装死吧。
—
谢邀。
我不属于公募或券商自营以及国家队的交易员,无从谈体验。〈注:以下交易员专指,公募或券商自营以及国家队的交易员〉
只能谈谈对于他们操盘手法的看法。先总结:他们这次是把交易员仅存的一丝尊严与颜面也丢光了。
晚上抽空细说。
好。我们来谈谈。
是次救市对错与否先放一边,监管部门之前的昏招叠出亦放一边,之前之种种都与交易员无关,而本次救市最大之动作是从周末的紧急会议开始,有两点措施是最为有力的:
①券商在及其不情愿下被要求出资合计1200亿。
②央行为证金公司提供未具额度流动性。
至此交易员们将要登上舞台了,其“光荣与梦想也即将被见证”。
何为救市关键?自然是砸下资金,以求稳定市场信心。可以说在周一开盘前资金—―这一救市最关键之要素已具备,接下来就是打法。
回到正题。
为什么说:“他们这次是把交易员仅存的一丝尊严与颜面也丢光了。”
在占尽信息优势、资金优势甚至道德优势的情况下,在错误的时间、错误的地点、用错误的手段打了一场惨不忍睹、颜面尽失的不对称败仗。
分别来说:
①错误的时间,竟然于集合竞价时段动用宝贵的资金,大量挂涨停价封住个股,甚至IC500期指都一度封于涨停。到底是谁下的如此愚不可及的命令。用如此自杀式手法,无异于摇旗号召大家来做空IC。
②错误的地点,如果说早盘封停IC做法,是妄图迅速解决战斗,赚尽眼球,强力挽回市场信心,还有情可原。那下午专注硬拉IH50系列,何止是愚蠢简直就是荒诞。敢情半天了都没弄清楚市场信心源于何处。IH你不动它都不会崩跌太多,而关键是IC500系列啊,这才是信心之源,稳住IC恢复流动其流动性,让大量要出来的资金轻松撤离,自然而然也就止住了整个大盘崩跌之势。因为IC是影响了市场广泛的参与者,特别是大量机构与私募及融资盘,这些资金顺利撤离,被动做空也就无从谈起。而浪费资金在IH50能一时稳住上证,也不可能持续在IC暴跌情况下独善其身。
③错误的手段,以历来各国、各地区救市之经验来看,你不能指望在股市以成崩溃之势时,意图迅速扭转趋势,力挽信心缺失狂澜。如早盘的打涨停板,与下午的硬拉,这都是无故浪费宝贵救市资金之举,高开低走下来反而更会造成隔天恐慌性大规模抛盘。正确的做法是,开源引流,有充裕的救市资金,而不硬拉,只稳住盘面震荡或缓跌即可,让风险缓释,而我们可爱的交易员门却急于完成任务或造就市场奇观,一会儿淹死一会儿渴死,如此如何挽回市场信心,不造成更大恐慌已是万幸,哪怕市场本来有得救,也被如此手法给结果了。
券商自营与公募交易员其尊严在于,每个交易员所在团体本来都有独立、自由决策交易之权力;虽然公募往往在意业内排名,不重视绝对收益,而券商自营不论规模大小,均为自家核心力量一部。国家队交易员之尊严在于,汇金、证金都作为国家意志稳定市场之力量存在,而自豪感油然而生,虽然是投入之资金往往效率奇低。而是次救市券商自营与公募独立、自由决策交易之权力被无情剥夺;国家队交易员作为稳定市场之力量而无能为力,反而造就更为剧烈的波动与恐慌。因而他们仅存的一丝尊严与颜面也丢光了。
待补充……..
黎曼zeta 黎曼球可以看作复数平面上缠一个球体 锥面上顶点处的曲率等于无穷大("频谱分析"),其余点的曲率为0; 從雙曲曲面剪取的一片,其高斯曲率恒等於負一, 反過來說曲率等於負一的曲面與雙面曲面局部相等
phymath999: 频谱分析是可能证明黎曼猜想的途径;复数放在 ...
phymath999.blogspot.com/2013/01/blog-post_7808.html
轉為繁體網頁
2013年1月18日 - 黎曼猜想是什么(2) 2. 算术基本定理与黎曼zeta函数。 算术基本定理又叫唯一分解定理。这个定理是说,每一个大于1的正整数N都可以写成有限个
phymath999.blogspot.com/2013/01/blog-post_7808.html
轉為繁體網頁
2013年1月18日 - 黎曼猜想是什么(2) 2. 算术基本定理与黎曼zeta函数。 算术基本定理又叫唯一分解定理。这个定理是说,每一个大于1的正整数N都可以写成有限个 轉為繁體網頁
科学网—相对论与黎曼几何-9-平行移动和曲率- 张天蓉的博文
blog.sciencenet.cn/blog-677221-831653.html
轉為繁體網頁
2014年9月29日 - 二维曲面上的平行移动和曲率 根据上节最后得到的“无限小”平行移动公式,理论上便知道了如何将一个矢量的坐标分量改变 ... 相对论与黎曼几何-9-平行移动和曲率 精选 .... 因此,锥面上顶点处的曲率等于无穷大,其余点的曲率为0。
blog.sciencenet.cn/blog-677221-831653.html
轉為繁體網頁
2014年9月29日 - 二维曲面上的平行移动和曲率 根据上节最后得到的“无限小”平行移动公式,理论上便知道了如何将一个矢量的坐标分量改变 ... 相对论与黎曼几何-9-平行移动和曲率 精选 .... 因此,锥面上顶点处的曲率等于无穷大,其余点的曲率为0。轉為繁體網頁
黎曼球面Riemann sphere对冲基金数学模型方法_柳州文铮_ ...
blog.sina.com.cn/s/blog_7f6f656101018wjb.html
轉為繁體網頁
2012年9月24日 - 这个扩展的平面表示扩展的复杂数字 ,即, 复数加一个值∞为无穷大 。 ... 球体与任何紧凑黎曼面,也可能被视为一个射影代数曲线 ,使它代数几何中 ...
blog.sina.com.cn/s/blog_7f6f656101018wjb.html
轉為繁體網頁
2012年9月24日 - 这个扩展的平面表示扩展的复杂数字 ,即, 复数加一个值∞为无穷大 。 ... 球体与任何紧凑黎曼面,也可能被视为一个射影代数曲线 ,使它代数几何中 ...轉為繁體網頁
黎曼度规[http://867107157.qzone.qq.com]
user.qzone.qq.com/867107157/blog/1350126974
轉為繁體網頁
2012年10月13日 - 黎曼度规. 在黑暗的度规中隐藏着鲜为人知的密秘. Kurt Goldel ... 2 0乘以无穷无穷减去无穷( 应为无穷大于无穷小成倒数的关系)所以无穷大都写成 ...
user.qzone.qq.com/867107157/blog/1350126974
轉為繁體網頁
2012年10月13日 - 黎曼度规. 在黑暗的度规中隐藏着鲜为人知的密秘. Kurt Goldel ... 2 0乘以无穷无穷减去无穷( 应为无穷大于无穷小成倒数的关系)所以无穷大都写成 ...轉為繁體網頁
黎曼猜想
159.226.2.2:82/gate/big5/www.kepu.net.cn/gb/.../2_25_1016.htm
希爾伯特回答:“我會先問黎曼猜想是否已經獲得解決了?” 原來他在1900年把這問題 ... 人們早知道下面的調和級數是不收斂(即和是無窮大)。 在1737年左右歐拉引進 ...
159.226.2.2:82/gate/big5/www.kepu.net.cn/gb/.../2_25_1016.htm
希爾伯特回答:“我會先問黎曼猜想是否已經獲得解決了?” 原來他在1900年把這問題 ... 人們早知道下面的調和級數是不收斂(即和是無窮大)。 在1737年左右歐拉引進 ...黎曼曲面_好搜问答 - 奇虎
wenda.haosou.com/search/?q=黎曼曲面&src=tab...pn... - 轉為繁體網頁
黎曼流形和黎曼几何,虽然黎曼面是一个一维复流形。黎曼 ... hold on;n=100;%这个数你自己定,反正到无穷大是不可能了for i=2:n j=1:i-1; j=j(gcd(i,j)==1); plot(j/i,1/i,'r.
wenda.haosou.com/search/?q=黎曼曲面&src=tab...pn... - 轉為繁體網頁
黎曼流形和黎曼几何,虽然黎曼面是一个一维复流形。黎曼 ... hold on;n=100;%这个数你自己定,反正到无穷大是不可能了for i=2:n j=1:i-1; j=j(gcd(i,j)==1); plot(j/i,1/i,'r.黎曼球可以看作复数平面上缠一个球体(通过某种形式的立体投影

一个几何球体上的两个方位线之间的区域。
图片来源:KARTHIK Narayanaswami
The region between two
Image credit: Karthik Narayanaswami

黎曼球可以看作复数平面上缠一个球体(通过某种形式的立体投影
在数学中
扩展复数复杂的分析是有用的,因为它们允许零
在几何的黎曼领域是一个黎曼曲面的典型例子,是一个最简单的复流形
扩展复数
扩展复数由的复数C一起∞。
几何上,扩展的复数的组被称为为黎曼球体
加复数可以延长定义为
任何复数
所有非零复数
任何有理函数的 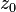

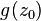

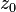

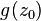

例如,给定的功能
我们可以定义
当看作是一个复杂的多方面的,合理的功能,其实是全纯函数的黎曼球本身。
直观地说,过渡地图显示如何胶水两架飞机一起,形成黎曼球。
在拓扑上
另一方面,
所有非零复数λ。
C的坐标ξ的另一个副本可以被映射到由
这两个复杂的图表涵盖了投影线。
表明过渡映射ζ= 1 /ξ和ξ= 1 /ζ,如上。
Riemann球形可以作为单位球面上的可视化X
同样,从(0,0,-1)的立体图投影到平面
为了掩盖的单位球,需要两个立体的预测:第一个将覆盖整个领域,除了点(0,0,1)和第二点(0,0,-1)除外。
ζ-坐标和ξ坐标的过渡之间的映射是通过以下方式获得构成一个突起与其他逆。
在此微分同胚,在单位圆中的ζ图,ξ图的单位圆,赤道单位球面的确定。
一个黎曼面不配备任何特定的黎曼度量
在一个给定的保形类,可以使用形对称性找到一个方便性能指标代表。
在黎曼球的情况下, 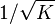
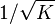
在实际坐标ζ=
最多一个常数因子,这个衡量标准与标准的富比尼研究度量复射影空间(其中的黎曼球就是一个例子)。
相反,,让S表示球体(作为一个抽象的平稳或拓扑流形
任何数学对象的研究,借助于其基团的同构的理解,这意味着从对象到其自身的地图,保存的基本结构的对象。
莫比乌斯变换盈利看作是复杂的投影线的转换。
如果赋予黎曼球面与富比尼-研究公制
在复杂的分析,亚纯函数在复平面上(或任何黎曼曲面上,对这一问题)是一种比F / G的两个全纯函数
黎曼球在物理学有许多用途。
| 本文包含一个列表的引用 |
| 本文列举了它的来源 |
布朗,詹姆斯和丘吉尔,鲁埃尔(1989年),
格里菲思,菲利普·哈里斯,约瑟夫(1978年)。
彭罗斯,罗杰
鲁丁,瓦尔特(1987年)。
[
Hazewinkel,米歇尔,编辑。
莫比斯转换揭晓
古典的幾何學者在討論三維空間中的曲面時,他們留意到曲面上每一點的曲率,都有兩個不同的選擇。比如在一個圓柱面上,一個方向是沿其橫切的圓,另一個則是沿垂直線。高斯在1827發現這兩個曲率的乘積具有驚人的屬性。當我們另曲面在空間變型,只要它沒有拉長縮短,這個積是不變的!後世稱這個積為高斯曲率
[PPT]請點選此處下載。
mathcenter.ck.tp.edu.tw/Resources/Ctrl/ePaper/ePaperOpenFileX.ashx?...
2005年11月15日 - 雙曲幾何給出第一個抽象而與歐氏不一樣的空間,影響到黎曼的工作。 .... 張量滿足等價原理,黎曼曲率使得度量拉長或收縮,正符合他的需要。 ... 物理中的等價原理要求引力的定律與座標的選取無關,黎曼的曲率正正具有這種特性。[PPT]近代幾何的發展 丘成桐香港中文大學數學科學研究所
www.cms.zju.edu.cn/UploadFiles/AttachFiles/20054411421524.ppt
在空間每一點都可以變動的內積,即是說給出了黎曼度量,可以寫作一個張量 。 ... 在一般的黎曼幾何裏,兩點 p 和q 之間可以有超過一條的路徑使得E(x) 是極短的。 ... 在 t 0 ,熱方程的核可以用擾動的方法計算出來,它跟空間的曲率有關,因此指標可由曲率表示, .... 單連通的定義是說在此空間中任何一個閉曲線可以連續收縮成一點。博研联盟.__.2005-几何三十载_百度文库
wenku.baidu.com/view/212730d276eeaeaad1f330d9.html?re=view
2011年3月22日 - 0 在空間每一點都可以變動的內積,即是說給出了黎曼度量, 可以寫作一個張量? i ... 3 在一般的黎曼幾何裏,兩點p 和q 之間可以有超過一條的路徑使得E(x) 是極短的。 ... 0 ,熱方程的核可以用擾動的方法計算出來,它跟空間的曲率有關,因此指標 .... 單連通的定義是說在此空間中任何一個閉曲線可以連續收縮成一點。庞加莱猜想100年 - 欢迎访问科学文化评论 - 中国科学院
sourcedb.scr.cas.cn/zwqkk/.../t20091123_2673455.html
轉為繁體網頁
2009年11月23日 - 高斯的确做过这种测量,但测量误差使他无法做出判断。 ... 在向高维推广时,这缺点更加突出,尤其是当只是“粗线条”地了解图形的时候。 ... 主要的一个是单连通性,也就是球面上任何一个绳圈都可以在球面上连续地变形,最后收缩成一点。 .... 把黎曼轉為繁體網頁
[PDF]to download the PDF file. - 中研院數學研究所
w3.math.sinica.edu.tw/math_media/d232/23201.pdf
Euler-Lagrangian 方程, 即黎曼泛函的. 臨界度量方程。 ... 的初值度量gij(0) 的Ricci 曲率是正的, 則 ... 的解沿著正. Ricci 曲率的方向向內收縮(shrinking); 然 ... 例如在S2科学网—相对论与黎曼几何-15-引力场方程- 张天蓉的博文
blog.sciencenet.cn/blog-677221-843310.html
轉為繁體網頁
2014年11月14日 - 就像是天意安排的,格罗斯曼后来成为黎曼几何专家。 ... 观测者测量直径的时候,轉為繁體網頁
從球面剪取一片曲面,其高斯曲率為正常數。反過來說,局部而言,任何具正常曲率的曲面都是球面的一部分。
類似地,從雙曲曲面剪取的一片,其高斯曲率恒等於負一,而反過來說曲率等於負一的曲面與雙面曲面局部相等。雙曲曲面曾在討論歐氏第五公設時論及算術基本定理與黎曼zeta函數 送交者: 莊銳 2013年01月12日16:19:17 于 [教育學術] 發送悄悄話
黎曼猜想是什麼(2)
2. 算術基本定理與黎曼zeta函數。
算術基本定理又叫唯一分解定理。這個定理是說,每一個大于1的正整數N都可以寫成有限個質數(或者素數)的乘積;這個乘積叫做N的因數分解。N的因數分解中的質數因子可以有重復但是其個數是由這個被分解的正整數確定的,不同整數的分解是不可能相同的。這個定理幾乎有兩千年的歷史。 算術基本定理描述了全體素數是整個大于一的正整數之集合的生成集;就是說從所有素數的集合出發,把所有有限乘積都加進去就得到了所有大于1的正整數之集合。
描述質數之個數的結論叫做素數定理,這個定理根據估計的準確度可以有多種不同的形式。固定任何一個比一大的正整數N,通過簡單的實驗人類很早就知道在一到N之間我們可以期待有少數質數。比如在1到10之間有2,3,5,7這四個質數;佔幾乎五分之二。 這個比例平均地講隨著N的增加在減少,實驗結果告訴我們在一到N之間大概有 M =log(N) 分之一的整數是質數。這里的 log(N) 是類似與常用對數的(以e為底的)自然對數。這個e是繼圓周率pi之後的第二個重要數學常數。用公式表示,通常把從一到N之間的質數個數表示為 pi(N)。這里的 pi 用的是圓周率的同一個符號,但是不是指那個圓周率常數,而是用來表示質數計數函數。 最簡單的素數定理是說 pi(N) 大致等于N 與 log(N) 的商。 這里的大致必須用數學詞匯準確地描繪。 其他精確的素數定理就要給出對這個函數的更精確描寫加上對誤差的估計。
在黎曼之前,高斯對質數計數函數有一個猜測,那就是用現在叫做 高斯的(logarithmic integral) 對數積分函數 li(N) 來代替上面所提到的N與log(N)之商。高斯對後來叫做黎曼zeta函數的那個數學對象已經有過一些研究。1859年,黎曼在他唯一關于數論的研究論文中引進復數作為變量,從而制造出現在叫做黎曼zeta函數的這個特殊函數。黎曼zeta函數是一個以復數為變量的函數,除了一個奇點以外這個函數在整個復數平面上是解析的。這里用的的“解析”一詞,基本上就是微積分中無窮次可微分的意思。
要解釋什麼是黎曼zeta函數,我們還是從如何計算質數的個數說起。 數學發展到前兩個世紀中間的時候,已經有了非常成熟的無窮個數字相加的工具。 其實幾乎兩千年前就有“一尺之棰,日取其半,萬世不竭”的說法。如果把二分之一,四分之一,八分之一,十六分之一,等等一切,一直加起來,可以想象其和為一。 嚴格地說,這就是現代數學系大學高年級里學到的“無窮級數”。定義黎曼zeta函數就必須要用到“無窮級數”與“解析”的概念,所以至少要到大學數學系接近畢業的學人們才可能真正理解黎曼zeta函數的定義。
這里給出在某個場合本人曾經使用過的一個籠統解釋,那就是黎曼zeta函數其實就是把所有的正整數添加必要的附帶數據後然後巧妙地糅合在一起得到的一個函數。不難想象,有關整數的所有一切都被揉在里面了。 因此可以說,這個函數既展示了宇宙的完美無瑕,又顯現出這個世界的雜亂無章。 對于數學家們的問題就是,如何從這個非常復雜的函數里面找到清晰的數學數據。
既然有無窮個質數存在,我們可以比如用每一個正整數的倒數來相加。事實上,所有正整數的倒數相加起來叫做調和級數。調和級數的和仍然是一個無窮大;而這正是黎曼zeta函數中唯一一個奇點的來源。如果把所有正整數的平方的倒數加起來,那麼得到的結果等于那個圓周率的平方除以6。這樣用來研究質數個數的黎曼zeta函數與圓周率也有著緊密的聯系。事實上,所有的數學理論都是緊密地聯系在一起的。作為開端,黎曼zeta函數被定義為所有正整數的其復數變量次方的和,比如我們必須定義2的pi次方是什麼意義。但是這個定義只對復數變量的實數部分大于一的時候有用,然後就要進行進一步的解析延拓把這個函數對所有復數變量都給予定義。除了在復數變量為一的時候為無窮大以外,其他所有復數變量對應的函數值都是有限的。這就是對于什麼是黎曼zeta函數的一個簡單解釋。
相關鏈接︰
| 黎曼猜想是什麼(1) |
直积与张量积的数学定义与物理定义异同
| 新用户注册 | 用户登陆 | 刷新 |
| 萍踪浪迹 发表文章数: 1051 内力值: 453/453 贡献度: 9137 人气: 1200              |
标题: 直积与张量积的数学定义与物理定义异同
作者: 萍踪浪迹 前言:此文修正了过去主帖的武断观点,并且将若干回帖合并,然后扩充成文。说数学定义与物理定义的异同,不是指数学上和物理上的定义之间有区别,而是数学家内部都有争议,物理学家内部也有类似争议。 直积的思想背景来自Descartes,因此被称为Descartes积(Cartesian product)。直积有时候称为“完全直积”,以区别于“离散直积”(就是直和)。因此有限个因子的直积就是离散积,因此也就是直和。直和只有在非 Abel范畴情形下才被称为“离散直积”。每个向量空间可以分解为一维子空间的直和。 张量积的定义有很多。 1)含单位元的结合交换环A上的两个幺模的张量积。若V_i,V_j是自由A模,e_i,e_j分别是V_i,V_j的基,那么(e_iⅹe_j)就是V_1与V_2的直积的基。如果V_i,V_j都是有限生成自由模,那么dim(V_iⅹV_j)= dimV_iXdimV_j。数域K上有限维向量空间就是有限生成模,所以就适用于这种情形。物理中经常用到的张量积也是这样定义的。我们可以把两个张量积的概念推广到多个甚至无限个的情形。 2)与上面定义相关的还有两个矩阵A与B的张量积,也称为Kronecker积。如果A的矩阵元为a_ij,B的矩阵元为b_mn,那么A与B的张量积的元素就是a_ij与b_mn分别相乘,形成的矩阵的行数就是im,列数就是jn。如果我们把矩阵A看为ij维空间,把矩阵B看成mn维空间,那么矩阵A与B的张量积就是ijmn维空间,与第一种定义是对应的。 3)(拓扑空间上)向量丛的张量积。各个向量丛的转移函数的矩阵张量积(Kronecker积)就是向量丛张量积的转移函数。 4)含幺结合单位环上的代数的张量积,这个与物理学的关系不算很大,因此不是我们关心的,暂时不谈论。 5)群表示的张量积。与拓扑群表示论密切相关,虽然拓扑群表示论与量子场论的关系很密切,但是这个不是这篇文章的主题,所以也不是我们现在要讨论的。 我们从上面的定义中可以看出,虽然张量积种类多种,但是前三种张量积基本上可以视为同一本质,都与直积严格区分。张量积与直积的区别是明显的。至少数学中的张量积与直积基本上(不完全)是泾渭分明的。 数学上基本上按照这些定义来区分张量积和直积。但是一些物理教科书和一些物理文献将直和与直积这两个“基本”上相同的概念作为两个完全不同的概念,前者对应了数学上的直和即离散直积,后者对应了数学上的张量积。马中骐教授的《物理学中的群论》的第一章的最后一节和喀兴林教授的《高等量子力学》的第一章最后一节,在讨论了矢量空间的直和与直积就是用了这种“约定”,将直和与直积区分,前者是数学上的直和(离散直积),后者是数学上的张量积。与此相类似的一些物理教科书上的这种约定使很多人尤其使学习物理的人产生了种种疑惑,例如看到两个空间的直积,就想到维数一定是这两个空间的乘积,而实际上维数应该使相加。 直积和直和在特定情况下的等价性,很多物理书没有提及,但是不妨碍这个事实成立。或许物理学家认为直接把矩阵元或者线性空间基底逐个相乘得出新空间,就是“直积”,直接把各个空间的基底个数相加后形成新空间坐标基,就是“直和”,这样理解是有道理的,但是不够规范。 虽然对于一部分物理学家,直积的概念不对应Descartes积,从而直接以直积作为张量积的代名词。但是并非所有物理学家都这样,甚至可以说只有少数物理学家遵循这样的约定俗成。 例如,我们可以在理论物理文献中发现大量诸如AdS_5ⅹS^5的写法,就是表示5维反de Sitter空间与5维球面的“直积”,维数却是10维,而不是25维。这里用乘号表示就已经足以说明大量物理学家认为这是直积,我尚未看见有人把这里的乘号换成直和符号,虽然二者的定义在这种情况下是完全一样的(都是有限维)。导致这个符号偏好的原因很大一部分在于物理学家也非常明了此时这个情况是将空间作为集合来定义Descartes积,于是自然采用了乘号,也就强调了这个操作的“积性”而非“加性”,至于加性,体现在所谓的直和分解中,维数可以用子空间维数逐个相加。另外在弦论中,我们也经常看到Minkowski空间与额外维空间(如Calabi-Yau空间)的类似的乘积符号,来定义它们的直积。 上面的例子直接说明大部分物理学家与绝大部分数学家一样,认定直和与直积在离散意义下的等价性,大部分物理学家定义的直积不是数学上的张量积或Kronecker积。 虽然很多学物理的人对张量积感到陌生,但是张量积的源头就在于张量这个概念,物理味道很浓,因为这个可以从张量分析甚至最初等的曲面微分几何中的最简单张量——度量(度规)张量中得到来源,因此对于物理学家其实不算陌生概念。在我们非常熟悉的度规张量的构造中,就是直接将切矢量的基底逐个相乘后作为基底。 例如曲面情形,切空间就是切平面,两个线性无关的切矢量张成切平面,基底分别相乘,就形成2X2=4个新基底,在四维(3,1)伪Riemann空间,即 Lorentz流形的情形,就是四个线性无关的切矢量基张成四维切空间,基底分别相乘,即称为广义相对论中的4X4度规张量的基。这个构造方式的张量含义实在太明显了,因此称为“张量积”是顺理成章的。或者可以说,我们对切空间坐标基逐个取“并矢”,就构成新空间的坐标基,因此张量积的物理意义非常明显,至少对于学过相对论的人而言是这样。 在更抽象的整体微分几何中,必然讨论微分流形代数结构,也就必然要讨论张量积,就是多重线性代数而已,粗略说,定义方式类似于局部微分几何时度规张量的基底构造,以映射的观点定义Riemann曲率张量以及Ricci曲率张量。 综合上面所说,直和直积与张量积在数学与物理不同文献上的异同只是名称约定问题,不存在定义方式的问题。只要是维数直接相乘的,就是数学上的张量积,也是一些物理文献和著作上的“直积”;维数直接相加的,就是一些物理书上的“直和”,也就是数学上的直和即离散直积。大家注意各自的定义方式,各取约定就可以轻松避免不必要的混淆了。至于它们的严格定义,教科书上或者百科全书上已经说得很清楚,不用我们在劳作了。 |


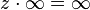
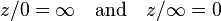

![黎曼球面Riemann <wbr>sphere对冲基金数学模型方法 \ {对齐} \ zeta电= 1 / \十一\ \ [8PT] \ XI = 1 / \泽塔。 \ {对齐}](http://upload.wikimedia.org/math/e/b/b/ebb2d659fa461362aaf1960142b0f066.png)





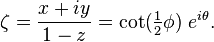
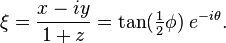
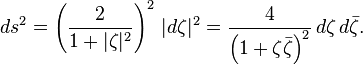
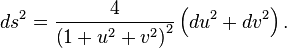

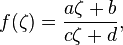

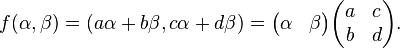
No comments:
Post a Comment