考虑角度亏损的时候，也不是只有一个角度亏损值，相对于每一个可能存在的转轴，都将有一个所谓角度亏损值。如此一来，n维流形上每一个点的曲率需要不止一个数值来描述。所以，我们便在每个点的切空间中定义一个曲率张量，或换言之，赋予黎曼流形上一个曲率张量场

相对论与黎曼几何-10-测地线和曲率张量 精选

已有 5429 次阅读 2014-10-9 07:57 |个人分类:系列科普|系统分类:科普集锦

10. 测地线和曲率张量

 

平行移动的概念不仅可以被用来定义曲面的曲率，也可以被用来定义测地线。

 

测地线是欧几里德几何中“直线”概念在黎曼几何中的推广。欧氏几何中的直线，整体来说是两点之间最短的连线，局部来说可以用“切矢量方向不改变”来定义它。将后面一条的说法稍加改动，便可以直接推广到黎曼几何中：

 

“如果一条曲线的切矢量关于曲线自己是平行移动的，则该曲线为测地线。”

 

第八节中曾经给出矢量V平行移动时在列维-齐维塔联络意义下的逆变分量坐标表达式：dV^j/ds+ G^j_npVⁿdx^p/ds= 0。根据上述测地线的定义，如果将其中的V^j用切矢量的分量（dx^j/ds）代替的话，便可得到用克里斯托费尔符号表示的测地线的方程。

                                                           

 

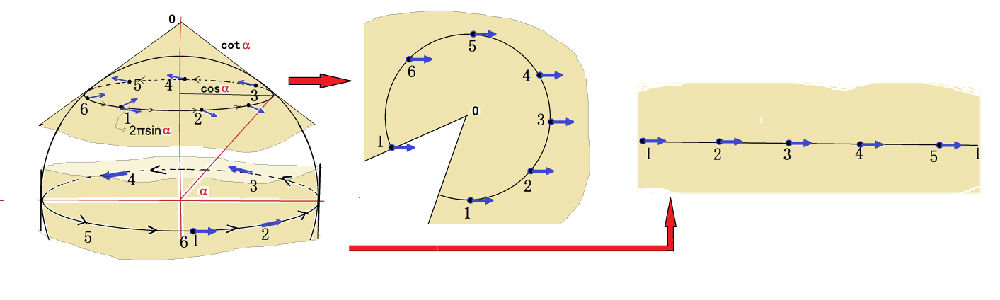
图2-10-1：在纬度a的圆上以及在赤道上切矢量的平行移动有所不同

 

以球面为例，我们可以利用上一节中采取的方法来研究切矢量的平行移动。一般来说，沿着球面上纬度为a的圆的平行移动等效于在一个锥面“帽子”上的平行移动。然而，当a=0时（对应于赤道），锥面变成了柱面，如图2-10-1左图所示。因而，可以将锥面或柱面（赤道）展开成平面来研究球面上的平行移动。图2-10-1中图和右图分别是锥面和柱面展开的平面上平行移动的示意图。。从两个图中可以看出，切矢量的平行移动对a=0（赤道）和a>0（非赤道）两种情形有所不同。对于小于赤道的圆，从锥面展开的平面图可知，点1的切矢量，平行移动到2、3、……各点后不一定再是切矢量；而赤道在柱面展开的平面图中是一条直线，所以，点1的切矢量平行移动到2、3、……各点后仍然是切矢量。

 

因此，如赤道这样的“大圆”，即圆心与球心重合的圆，符合我们刚才所说的测地线的定义：切矢量平行移动后仍然是切矢量。所有的大圆都是球面上的测地线。

 

测地线是否一定是短程线呢？对欧氏空间来说是如此，但对一般的黎曼空间不一定如此。比如球面上，连接两点的测地线至少有两条（一个大圆的两段），那条小于180度的圆弧是短程线，而另一部分，即大于180度的圆弧，就不是短程线了。不过，测地线是局部意义上的短程线，对于充分接近的两个点，测地线是最短曲线。

 

下面继续上一节有关曲率的讨论。

 

如前所述，2维曲面上某一点P的曲率R，被定义为“任意矢量沿曲面上无限小的闭曲线平行移动后的角度亏损对闭曲线所包围之面积的导数”，即：标量曲率R = dq/dA。以上的叙述中包含了如下几点概念：曲率R是局部的，随点P位置的变化而变化；曲率R的定义依赖于一个2维曲面；曲率R的定义与某个角度亏损有关。所谓角度亏损，就是矢量的方向平行移动后相对于原来的方向绕某一个轴转动的角度。

 

在2维曲面上的每个点，按照上面的方法，能定义一个曲率R。也就是说，定义了2维曲面上的一个标量曲率场。

 

现在，如果考虑一般的n维黎曼流形，就需要将上述的曲率概念加以推广。首先想到的是：在维数大于2的流形上的每一点，应该仍然可以局部地定义曲率。然而，如果按照2维曲率定义的方法，当n大于2时，不仅仅得到一个曲率值，而是可以定义多个曲率数值。其原因是因为对高维空间中的一点，通过它的二维面不止一个，另一方面，当我们考虑角度亏损的时候，也不是只有一个角度亏损值，相对于每一个可能存在的转轴，都将有一个所谓角度亏损值。如此一来，n维流形上每一个点的曲率需要不止一个数值来描述。所以，我们便在每个点的切空间中定义一个曲率张量，或换言之，赋予黎曼流形上一个曲率张量场。

 

下面需要考虑的是，这个曲率张量的阶数是多少？或者说，这个曲率张量应该有几个指标，才能表征n维黎曼流形在一个给定点的内蕴弯曲度？

 

图2-10-1：黎曼曲率张量和平行移动

 

可以用如下的方法将2维空间标量曲率概念推广到n维以上的流形。首先考虑n维流形中的矢量V在P点附近的平行移动方式。矢量V可以沿着过P点的任何一个2维子流形的回路平行移动。比如说，图2-10-1所示的是V在由坐标x^m和xⁿ表示的曲面上沿着dx^m、dxⁿ、-dx^m、-dxⁿ围成的四边形回路平行移动的情形。一般来说，当V绕回路一圈返回原点时将和原来矢量不一样，得到了一个改变量dV。类比于标量曲率R的定义，矢量的这个增量应该正比于平行移动的路径所围成的面积，即dx^mdxⁿ。除此之外，矢量增量dV还应该与原矢量V有关。考虑dV和V方向上的差异，增量dV的逆变分量dV^a可以写成如下形式：

 

dV^a= dx^mdxⁿV^gR_n^a_mg，                                   （2-10-1）

 

这儿，将平行移动一周之后的微小变化用符号d表示，以区别于坐标的线性微分增量dx^m或dxⁿ。

 

公式（2-10-1）中的比例系数R_n^a_mg，便是黎曼曲率张量。如前所述，四个指标中的两个m和n对应于平行移动路径所在的2维曲面，而另外两个指标a和g分别表示矢量增量dV及原来矢量V的逆变指标。公式右边的重复指标m、n和g是求和的意思，这是遵循以前提到过的“爱因斯坦约定”，以后用到重复指标时都是表示求和的约定，不再赘述。

 

黎曼曲率张量是个四阶张量，对n维空间，四个指标都可以从1变化到n，因而分量数目很多。但是由于对称性的原因，独立分量的数目大大减少，只有n²(n²-1)/12个。按照这个公式，当n等于4时，有20个独立分量；当n等于2时，曲率只有一个独立分量，这便是我们曾经介绍过的2维曲面的高斯曲率。

 

黎曼几何中有多种方式来理解和定义内在曲率的概念，下面将作一简单介绍。本来是同一个东西，从多种不同的角度看一看可以加深理解。就像是你在观察一座山：“横看成岭侧成峰，远近高低各不同”，多照几张照片才能帮助我们识得庐山真面目。上文中，用平行移动概念来定义的四阶黎曼曲率张量R_n^a_mg是定义曲率最标准的形式。黎曼曲率张量就像是给某座山某处附近照的标准照片，它的4个指标独立地变化，其取值范围都是从1到n，因而总的变化数目就有n⁴个，在n=4的情形下，这个数等于256。好比是在这附近照了256张照片，不过由于对称性，其中很多是重复的，不重复的只有20张。经专家们研究后认为，将整座山的每一个“局部景观”，都如法炮制地照出20张不重复的照片来，便能够作为这座山的完整描述。


之前，我们也曾经提到过“截面曲率”，它被定义为n维流形过给定点的所有2维截面高斯曲率的总和。截面曲率等效于黎曼曲率张量，与截面曲率有关的20张照片同样也是内蕴曲率的完整描述，但因为拍摄技术有所不同，有着更容易被人理解的直观几何解释。


不过，爱因斯坦在他的引力场方程中用到的，是另外两个称之为里奇曲率的几何量：里奇曲率张量R_μν和里奇曲率标量R，这两个曲率是通过上述黎曼曲率张量的指标缩并而得到的，将指标缩并的意思是什么？继续使用刚才的比喻，20张照片中，有些是相似的，因而可以首先挑选出更有代表性的一类，然后又将此类中的几张照片合并起来放到一张照片中。利用这种技巧，在某种条件下，将20张标准照简化到只用10张就够了。


比如说，里奇曲率张量就是由原来四个指标的黎曼曲率张量R_μ^a_ρν，将其中两个指标a和ρ缩并而成的二阶张量，写成：R_μν = R_μ^ρ_ρν。如果将原来黎曼曲率张量中4个指标中的两个（a和ρ）看成是矩阵的行列指标的话，那么，4阶黎曼曲率张量就等效于n²个2阶矩阵。进一步将矩阵的两个行列指标“缩并”：意思就是将这个矩阵只用一个数（它的trace）来表示。因而，指标缩并后，原来的n²个矩阵就变成了n²个数值，这就是所谓的里奇曲率张量。


里奇曲率标量呢，是由里奇曲率张量的两个指标再进一步缩并而成的一个标量：R= g^μνR_μν。在2维曲面情形下，R正好是高斯曲率的2倍。

这儿最后插上一段话，重申关于对“内蕴”的理解。高斯和黎曼的微分几何研究，强调的也是流形的“内蕴”性质。遗憾的是，受限于大脑的思维能力，我们无法用直观的图像来表达更为高维空间的这种“内蕴”性。唯一能加深和验证理解的直观工具就是想象嵌入在三维欧氏空间中的各种二维曲面。但我们务必要随时记住，在研究这些曲面的几何性质时，尽量不把它们当作三维欧氏空间中的子空间，而是把自己想象成生活在曲面上、只能看见这个曲面上发生的事件的“阿扁”，当我们从阿扁的角度来进行测量、考虑问题时，涉及的几何量便是“内蕴”几何量。然而，阿扁观测到的，只是2维曲面上的内蕴几何，研究维数更高的黎曼流形时，还需要使用另外一个诀窍。这个方法让我们更容易保持“内蕴”的思考，那就是：一切都得从度规张量出发。因为度规张量决定了几何中最基本的内蕴量：弧长，是黎曼几何的关键，有了度规张量后，便可以导出其它的内蕴几何量。

 

理解黎曼几何和广义相对论的另一个重要原则就是，物理规律要与坐标系无关。尽管任何有用处的实际计算都是在某个坐标系下面进行的，但计算结果表达的物理定律却是独立于坐标而存在。这也就是我们总是要将描述物理规律的方程式写成“张量”形式的原因，因为张量的坐标分量在坐标变换下作线性齐次变换。线性表明张量属于切空间，齐次表明张量与坐标系选择无关。如果一个张量在某个坐标系下所有分量都是零，经过线性齐次变换后，它在任何坐标系中都将是零。

在此也顺便回顾和总结下我们介绍黎曼几何的过程。黎曼流形（伪黎曼流形）是定义了一个对称正定（不正定）度规张量场g_ij的微分流形。为了在黎曼流形上作微分运算，需在相邻点的切空间之间引进“联络”的概念，具体地说，就是用列维-齐维塔联络，将不同切空间中的不同的度规张量关联起来。而作为列维-齐维塔联络坐标表达式的克里斯托费尔符号，只与度规张量和度规张量的微分有关。然后，我们定义了在列维-齐维塔联络意义下的协变微分和平行移动。引进协变微分的目的是为了定义张量之间的微分规则，以确保张量的协变微分仍然是一个张量。因为从协变微分而定义的平行移动与空间的“不平坦”程度密切相关，从而便由平行移动定义了测地线以及各种曲率的概念。


补充：有关平行移动
“如何平行移动”及“角度的变化”都是内蕴观察量，与被嵌入的空间无关。但为了更为直观的说明问题，画出的图只能是嵌入三维空间的二维面，比如下图b中的球面：


上图是在平面和球面上分别作平行移动的例子：女孩从点1到点2再到点3，一直到点7，作平行移动一圈后回到点1（1和7是同一点）。所谓‘平行移动’的意思是说，她在移动的时候，尽可能保持身体（或是她的脸）相对于身体的中心线没有旋转。这样，当她经过1、2、3……回到1的时候，她认为她应该和原来出发时面对着同样的方向。她的想法是正确的，如果她是在平面上移动的话（图a）。但是，假如她是在球面上移动的话，她将发现她面朝的方向可能不一样了！图b中红色箭头所指示的便是她在球面上每个位置时面对的方向。从图中可见，出发时她的脸朝左，回来时却是脸朝右。

上一篇：平行移动和曲率

系列科普目录

下一篇：等效原理

本文引用地址：http://blog.sciencenet.cn/blog-677221-834151.html  此文来自科学网张天蓉博客，转载请注明出处。
上一篇：相对论与黎曼几何-9-平行移动和曲率
下一篇：相对论与黎曼几何-11-等效原理

更多

收藏 分享 举报

当前推荐数：12 推荐人： 罗德海 应行仁 文克玲 李学忠 黄永义 沈律 许文龙 胡洪涛 qiue jiareng ybyb3929 ychengwei

该博文允许注册用户评论 请点击登录 评论 (9 个评论)

[9]ybyb3929  2014-10-10 08:45

6楼，比较才是数学的基础，正是因为有了方向的比较才有了“矢量”之一概念，而平行移动这些概念是方向比较加运动的结果，而那些所谓“内蕴观察量”是还没有搞明白矢量这一概念的来历的结果。

[8]ybyb3929  2014-10-10 08:39

我的结论就是：测地线是数学家为了忽悠世界人民，将直线偷偷换了概念而制造出了一个像是直线又不是直线的概念而已
博主回复(2014-10-9 18:14)：不是这样的 
___________________________我这句“测地线是数学家为了忽悠世界人民”话有点讲过火了，的确数学中存在无意之中偷换概念而造成数学发展出现问题。
没办法，要反数学了，民科不仅反相、反量，还要反数学了。
博主回复(2014-10-9 18:14)：造反派？
————————————————————————
推翻相对论就已得罪不少了人了，本不想再反数学，再得罪更多的人，但又不得不反，因为数学的确出现问题。

[7]张林  2014-10-9 19:03

谢谢补充的内容，我的问题是：平行的定义是相对于自己那个点的局域坐标系而言的，这个局域坐标系是欧氏的吧？她虽然在局域似乎没有转动，但我们整体上在欧氏空间看是转了！内蕴的含义没有想清楚。谢谢张老师

博主回复(2014-10-9 19:21)：平行移动的定义不是相对局域欧氏空间而言的，张量是对欧式空间而定义的。这就是为什么平行移动与联络（克里斯托费尔符号）有关。联络的目的就是将这些不同的欧氏坐标“联络”起来，以便定义微分运算。

[6]张林  2014-10-9 17:04

博文一如既往有货。但对于这个问题一直有个疑惑：矢量的平行移动。在曲面上平行移动一个矢量为什么最后有一个几何角出现。请问这个平行移动是在欧几里德空间中定义的，还是在黎曼空间定义的，平移在黎曼空间应该不存在(还是以欧氏空间看的)，所以似乎这个几何角是欧氏空间的结果，不知道对不对？

博主回复(2014-10-9 18:12)：“如何平行移动”及“角度的变化”都是内蕴观察量，是在黎曼空间里定义的，与被嵌入的欧氏空间无关。见我在文中新加的部分。