Thursday, December 3, 2015

riemann 黎曼定义的 “n 维流形” 大概是这个样子的：以其中一个点为基准，则周围每个点的位置都可以用 n 个实数来确定。后人将这种性质总结为：流形的局部与 n 维欧氏空间的局部具有相同的拓扑性质

黎曼定义的 “n 维流形” 大概是这个样子的：以其中一个点为基准，则周围每个点的位置都可以用 n 个实数来确定。后人将这种性质总结为：流形的局部与 n 维欧氏空间的局部具有相同的拓扑性质

拓扑学简介（四）—— 流形Comments>>

季候风发表于 2009-12-30 13:20 | Tags 标签：n 维流形, 原创, 拓扑学, 黎曼

拓扑学简介（一）拓扑学简介（二）拓扑学简介（三）
1854年，28岁的黎曼在哥廷根大学发表就职演讲。这个职位是所谓无薪讲师，他的收入完全来自于听课的学生所缴纳的学费。即使是争取这样一个职位，也需要提供一篇就职论文以及发表一个就职演讲。1853年他提交了就职论文，其中讨论了什么样的函数可以展开成三角级数的问题，并导致对定积分的第一个严格数学定义。之后的就职演讲要求候选人准备三个演讲课题，委员会从中挑选一个作为正式演讲题目。黎曼选了两个思虑多时的课题，外加一个还未及考虑的课题 ——关于几何学的基本假设。他几乎确信委员会将挑选前面两个题目之一。然而，委员会的高斯偏偏就看中了第三个题目。当时黎曼正沉浸于电、磁、光、引力之间的相互关系问题，从这样的深沉思考中抽身转而研究新的问题无疑是一种巨大的压力，再加上长期的贫穷，一度让黎曼崩溃。但不久他就重新振作起来，用 7 个星期时间准备了关于几何学基本假设的演讲。为了让数学系以外的委员会成员理解他的演讲，黎曼只用了一个公式，并且忽略了所有计算细节。尽管如此，估计在场鲜有人能理解这次演讲的内容。只有高斯为黎曼演讲中蕴含的深邃思想激动不已。
黎曼在演讲中提出了 “弯曲空间” 的概念，并给出怎样研究这些空间的建议。 “弯曲空间” 正是后世拓扑学研究的主要对象。在这些对象上，除了可以运用代数拓扑的工具，还可以运用微积分工具，这就形成了 “微分拓扑学”。
回到黎曼的演讲。黎曼认为，几何学的对象缺乏先验的定义，欧几里德的公理只是假设了未定义的几何对象之间的关系，而我们却不知道这些关系怎么来的，甚至不知道为什么几何对象之间会存在关系。黎曼认为，几何对象应该是一些多度延展的量，体现出各种可能的度量性质。而我们生活的空间只是一个特殊的三度延展的量，因此欧几里德的公理只能从经验导出，而不是几何对象基本定义的推论。欧氏几何的公理和定理根本就只是假设而已。但是，我们可以考察这些定理成立的可能性，然后再试图把它们推广到我们日常观察的范围之外的几何，比如大到不可测的几何，以及小到不可测的几何。接着，黎曼开始了关于延展性，维数，以及将延展性数量化的讨论。他给了这些多度延展的量（几何对象）一个名称，德文写作 mannigfaltigkeit, 英文翻译为 manifold，英文字面意思可以理解为 “多层”，中国第一个拓扑学家江泽涵把这个词翻译为 “流形”，取自文天祥《正气歌》，“天地有正气，杂然赋流形”，而其原始出处为《易经》，“大哉乾元，万物资始，乃统天。云行雨施，品物流形。” 这个翻译比英文翻译更加符合黎曼的原意，即多样化的形体。
黎曼定义的 “n 维流形” 大概是这个样子的：以其中一个点为基准，则周围每个点的位置都可以用 n 个实数来确定。后人将这种性质总结为：流形的局部与 n 维欧氏空间的局部具有相同的拓扑性质。如果进一步要求在流形的不同局部做微积分的结果可以互相联系起来，成为 “整体微积分”，则称此流形为 “微分流形”。一个简单的例子就是二维球面。我们都知道，二维球面上没有整体适用的坐标。经度和纬度是一组很好的坐标，但是在南北两极，经度无从定义。尽管如此，球面的每个局部都可以画在平面上，这就是地图。把各个区域的地图收集在一起，重叠的部分用比例尺协调一下，就得到整个球面。这样，坐标（或地图）只存在于每个局部，而整个球面其实是地图之间的重叠关系。球面是二维流形，因为球面的局部同平面（二维欧氏空间）的局部具有相同的延展性质。球面的整体结构显然跟平面不同。沿着球面的某个方向往前走，比如，从赤道某点出发往东走，最终会回到出发点。而如果在平面上沿某个方向往前走则永不回到出发点。研究流形的整体结构，以及整体结构与局部结构之间的关系，就是 “拓扑学” 的核心课题。微分流形上可以使用微积分的工具，再辅之以前面介绍过的代数工具（同调群，同伦群），就形成了威力强大的 “微分拓扑学”。这门学问的发展使我们对 5 维以上的单连通微分流形（回忆先前介绍的 “单连通” 概念，即每条曲线可于流形内滑缩为一点）有了比较彻底的认识。
到了80年代，数学家对 4 维单连通 “拓扑流形” 也有了彻底的认识，然而 4 维 “微分流形” 却是无比复杂的对象。比如，直观上最简单的四维流形，四维欧氏空间，也就是所有 (x,y,z,t) 这样的数组组成的空间，有无穷多个“微分结构”，通俗一点说，这个流形上有无穷多种 “整体微积分” 可做，而我们通常做的四元微积分只是其中一种。这是 4 维的特殊性，因为其他维数的欧氏空间都跟我们的常识相符。也许 “4” 就是传说中的上帝之数，我们的宇宙就是用 4 个参数来描述的（3个参数表示空间，1 个参数表示时间），我们的时空是一个四维流形。
如果我们忘掉时间，只考察我们生活的空间。它的形态会是怎样？这是黎曼在演讲结尾提出的问题。这个问题到现在还没有答案。这个答案需要物理学家、天文学家、宇宙学家去寻找。宇宙空间会不会是一个三维球面？如果是三维球面，那我们沿着一个方向往前飞行，最终总会回到起点

Exact solutions in general relativity

From Wikipedia, the free encyclopedia

Jump to: navigation, search

This article may be confusing or unclear to readers. Please help us clarify the article; suggestions may be found on the talk page. (March 2007)

General relativity

G_{\mu \nu} + \Lambda g_{\mu \nu}= {8\pi G\over c^4} T_{\mu \nu}

Fundamental concepts[show]

Phenomena[show]

Equations
Formalisms

[show]

Solutions[hide]

Scientists[show]

In general relativity, an exact solution is a Lorentzian manifold equipped with certain tensor fields which are taken to model states of ordinary matter, such as a fluid, or classical nongravitational fields such as the electromagnetic field. These tensor fields should obey any relevant physical laws (for example, any electromagnetic field must satisfy Maxwell's equations). Following a standard recipe which is widely used in mathematical physics, these tensor fields should also give rise to specific contributions to the stress–energy tensor

T^{\alpha\beta}

.^[1] (To wit, whenever a field is described by a Lagrangian, varying with respect to the field should give the field equations and varying with respect to the metric should give the stress-energy contribution due to the field.)
Finally, when all the contributions to the stress–energy tensor are added up, the result must satisfy the Einstein field equations (written here in geometrized units, where speed of light c = Gravitational constant G = 1)

G^{\alpha\beta} = 8 \pi \, T^{\alpha\beta}.

In the above field equations,

G^{\alpha\beta}

is the Einstein tensor, computed uniquely from the metric tensor which is part of the definition of a Lorentzian manifold. Since giving the Einstein tensor does not fully determine the Riemann tensor, but leaves the Weyl tensor unspecified (see the Ricci decomposition), the Einstein equation may be considered a kind of compatibility condition: the spacetime geometry must be consistent with the amount and motion of any matter or nongravitational fields, in the sense that the immediate presence "here and now" of nongravitational energy–momentum causes a proportional amount of Ricci curvature "here and now". Moreover, taking covariant derivatives of the field equations and applying the Bianchi identities, it is found that a suitably varying amount/motion of nongravitational energy–momentum can cause ripples in curvature to propagate as gravitational radiation, even across vacuum regions, which contain no matter or nongravitational fields.

[hide]

Difficulties with the definition[edit]

Take any Lorentzian manifold, compute its Einstein tensor

G^{\alpha\beta}

, which is a purely mathematical operation, divide by

8 \pi

, and declare the resulting symmetric second rank tensor field to be the stress–energy tensor

T^{\alpha\beta}

. Thus any Lorentzian manifold is a solution of the Einstein field equation with some right hand side. Which of course doesn't make general relativity useless, but only shows that there are two complementary ways to use it. One can fix the form of the stress–energy tensor (from some physical reasons, say) and study the solutions of the Einstein equations with such right hand side (for example, if the stress–energy tensor is chosen to be that of the perfect fluid, a spherically symmetric solution can serve as a stellar model). Alternatively, one can fix some geometrical properties of a spacetime and look for a matter source that could provide these properties. This is what cosmologists have done for the last 5–10 years: they assume that the Universe is homogeneous, isotropic, and accelerating and try to realize what matter (called dark energy) can support such a structure.
Within the first approach the alleged stress–energy tensor must arise in the standard way from a "reasonable" matter distribution or nongravitational field. In practice, this notion is pretty clear, especially if you restrict the admissible nongravitational fields to the only one known in 1916, the electromagnetic field. But ideally we would like to have some mathematical characterization that states some purely mathematical test which we can apply to any putative "stress–energy tensor", which passes everything which might arise from a "reasonable" physical scenario, and rejects everything else. Unfortunately, no such characterization is known. Instead, we have crude tests known as the energy conditions, which are similar to placing restrictions on the eigenvalues and eigenvectors of a linear operator. But these conditions, it seems, can satisfy no-one. On the one hand, they are far too permissive: they would admit "solutions" which almost no-one believes are physically reasonable. On the other, they may be far too restrictive: the most popular energy conditions are apparently violated by the Casimir effect.
Einstein also recognized another element of the definition of an exact solution: it should be a Lorentzian manifold (meeting additional criteria), i.e. a smooth manifold. But in working with general relativity, it turns out to be very useful to admit solutions which are not everywhere smooth; examples include many solutions created by matching a perfect fluid interior solution to a vacuum exterior solution, and impulsive plane waves. Once again, the creative tension between elegance and convenience, respectively, has proven difficult to resolve satisfactorily.
In addition to such local objections, we have the far more challenging problem that there are very many exact solutions which are locally unobjectionable, but globally exhibit causally suspect features such as closed timelike curves or structures with points of separation ("trouser worlds"). Some of the best known exact solutions, in fact, have globally a strange character.

Types of exact solution[edit]

Many well-known exact solutions belong to one of several types, depending upon the intended physical interpretation of the stress–energy tensor:

Vacuum solutions: 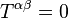$T^{\alpha\beta} = 0$ ; these describe regions in which no matter or nongravitational fields are present,

Electrovacuum solutions: $T^{\alpha\beta}$ must arise entirely from an electromagnetic field which solves the source-free Maxwell equations on the given curved Lorentzian manifold; this means that the only source for the gravitational field is the field energy (and momentum) of the electromagnetic field,

Null dust solutions: $T^{\alpha\beta}$ must correspond to a stress–energy tensor which can be interpreted as arising from incoherent electromagnetic radiation, without necessarily solving the Maxwell field equations on the given Lorentzian manifold,

Fluid solutions: $T^{\alpha\beta}$ must arise entirely from the stress–energy tensor of a fluid (often taken to be a perfect fluid); the only source for the gravitational field is the energy, momentum, and stress (pressure and shear stress) of the matter comprising the fluid.

In addition to such well established phenomena as fluids or electromagnetic waves, one can contemplate models in which the gravitational field is produced entirely by the field energy of various exotic hypothetical fields:

Scalar field solutions: $T^{\alpha\beta}$ must arise entirely from a scalar field (often a massless scalar field); these can arise in classical field theory treatments of meson beams, or as quintessence,

Lambdavacuum solutions (not a standard term, but a standard concept for which no name yet exists): $T^{\alpha\beta}$ arises entirely from a nonzero cosmological constant.

One possibility which has received little attention (perhaps because the mathematics is so challenging) is the problem of modeling an elastic solid. Presently, it seems that no exact solutions for this specific type are known.
Below we have sketched a classification by physical interpretation. This is probably more useful for most readers than the Segre classification of the possible algebraic symmetries of the Ricci tensor, but for completeness we note the following facts:

nonnull electrovacuums have Segre type 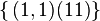$\{ \, (1,1)(11) \}$ and isotropy group SO(1,1) x SO(2),
null electrovacuums and null dusts have Segre type 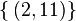$\{ \,(2,11) \}$ and isotropy group E(2),
perfect fluids have Segre type 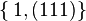$\{ \, 1, (111) \}$ and isotropy group SO(3),
Lambdavacuums have Segre type $\{ \, (1, 111)\}$ and isotropy group SO(1,3).

The remaining Segre types have no particular physical interpretation and most of them cannot correspond to any known type of contribution to the stress–energy tensor.

Constructing solutions[edit]

The Einstein field equation, when fully written out as a system of partial differential equations, takes the form of a rather complicated system of coupled, nonlinear partial differential equations. As such, in general, it is very hard to solve.
Nonetheless, several effective techniques for obtaining exact solutions are available.
The simplest involves imposing symmetry conditions on the metric tensor, such as stationarity (symmetry under time translation) or axisymmetry (symmetry under rotation about some symmetry axis). With sufficiently clever assumptions of this sort, it is often possible to reduce the Einstein field equation to a much simpler system of equations, even a single partial differential equation (as happens in the case of stationary axisymmetric vacuum solutions, which are characterized by the Ernst equation) or a system of ordinary differential equations (as happens in the case of the Schwarzschild vacuum).
This naive approach usually works best if one uses a frame field rather than a coordinate basis.
A related idea involves imposing algebraic symmetry conditions on the Weyl tensor, Ricci tensor, or Riemann tensor. These are often stated in terms of the Petrov classification of the possible symmetries of the Weyl tensor, or the Segre classification of the possible symmetries of the Ricci tensor. As will be apparent from the discussion above, such Ansätze often do have some physical content, although this might not be apparent from their mathematical form.
This second kind of symmetry approach has often been used with the Newman–Penrose formalism, which uses spinorial quantities for more efficient bookkeeping.
Even after such symmetry reductions, the reduced system of equations is often difficult to solve. For example, the Ernst equation is a nonlinear partial differential equation somewhat resembling the nonlinear Schrödinger equation (NLS).
But recall that the conformal group on Minkowski spacetime is the symmetry group of the Maxwell equations. Recall too that solutions of the heat equation can be found by assuming a scaling Ansatz. These notions are merely special cases of Sophus Lie's notion of the point symmetry of a differential equation (or system of equations), and as Lie showed, this can provide an avenue of attack upon any differential equation which has a nontrivial symmetry group. Indeed, both the Ernst equation and the NLS have nontrivial symmetry groups, and some solutions can be found by taking advantage of their symmetries. These symmetry groups are often infinite dimensional, but this is not always a useful feature.
Emmy Noether showed that a slight but profound generalization of Lie's notion of symmetry can result in an even more powerful method of attack. This turns out to be closely related to the discovery that some equations, which are said to be completely integrable, enjoy an infinite sequence of conservation laws. Quite remarkably, both the Ernst equation (which arises several ways in the studies of exact solutions) and the NLS turn out to be completely integrable. They are therefore susceptible to solution by techniques resembling the inverse scattering transform which was originally developed to solve the Korteweg-de Vries (KdV) equation, a nonlinear partial differential equation which arises in the theory of solitons, and which is also completely integrable. Unfortunately, the solutions obtained by these methods are often not as nice as one would like. For example, in a manner analogous to the way that one obtains a multiple soliton solution of the KdV from the single soliton solution (which can be found from Lie's notion of point symmetry), one can obtain a multiple Kerr object solution, but unfortunately, this has some features which make it physically implausible.^[2]
There are also various transformations (see Belinski-Zakharov transform) which can transform (for example) a vacuum solution found by other means into a new vacuum solution, or into an electrovacuum solution, or a fluid solution. These are analogous to the Bäcklund transformations known from the theory of certain partial differential equations, including some famous examples of soliton equations. This is no coincidence, since this phenomenon is also related to the notions of Noether and Lie regarding symmetry. Unfortunately, even when applied to a "well understood", globally admissible solution, these transformations often yield a solution which is poorly understood and their general interpretation is still unknown.

Existence of solutions[edit]

Given the difficulty of constructing explicit small families of solutions, much less presenting something like a "general" solution to the Einstein field equation, or even a "general" solution to the vacuum field equation, a very reasonable approach is to try to find qualitative properties which hold for all solutions, or at least for all vacuum solutions. One of the most basic questions one can ask is: do solutions exist, and if so, how many?
To get started, we should adopt a suitable initial value formulation of the field equation, which gives two new systems of equations, one giving a constraint on the initial data, and the other giving a procedure for evolving this initial data into a solution. Then, one can prove that solutions exist at least locally, using ideas not terribly dissimilar from those encountered in studying other differential equations.
To get some idea of "how many" solutions we might optimistically expect, we can appeal to Einstein's constraint counting method. A typical conclusion from this style of argument is that a generic vacuum solution to the Einstein field equation can be specified by giving four arbitrary functions of three variables and six arbitrary functions of two variables. These functions specify initial data, from which a unique vacuum solution can be evolved. (In contrast, the Ernst vacuums, the family of all stationary axisymmetric vacuum solutions, are specified by giving just two functions of two variables, which are not even arbitrary, but must satisfy a system of two coupled nonlinear partial differential equations. This may give some idea of how just tiny a typical "large" family of exact solutions really is, in the grand scheme of things.)
However, this crude analysis falls far short of the much more difficult question of global existence of solutions. The global existence results which are known so far turn out to involve another idea.

Global stability theorems[edit]

We can imagine "disturbing" the gravitational field outside some isolated massive object by "sending in some radiation from infinity". We can ask: what happens as the incoming radiation interacts with the ambient field? In the approach of classical perturbation theory, we can start with Minkowksi vacuum (or another very simple solution, such as the de Sitter lambdavacuum), introduce very small metric perturbations, and retain only terms up to some order in a suitable perturbation expansion—somewhat like evaluating a kind of Taylor series for the geometry of our spacetime. This approach is essentially the idea behind the post-Newtonian approximations used in constructing models of a gravitating system such as a binary pulsar. However, perturbation expansions are generally not reliable for questions of long-term existence and stability, in the case of nonlinear equations.
The full field equation is highly nonlinear, so we really want to prove that the Minkowski vacuum is stable under small perturbations which are treated using the fully nonlinear field equation. This requires the introduction of many new ideas. The desired result, sometimes expressed by the slogan that the Minkowski vacuum is nonlinearly stable, was finally proven by Demetrios Christodoulou and Sergiu Klainerman only in 1993. Analogous results are known for lambdavac perturbations of the de Sitter lambdavacuum (Helmut Friedrich) and for electrovacuum perturbations of the Minkowski vacuum (Nina Zipser).

The positive energy theorem[edit]

Main article: Positive energy theorem

Another issue we might worry about is whether the net mass-energy of an isolated concentration of positive mass-energy density (and momentum) always yields a well-defined (and non-negative) net mass. This result, known as the positive energy theorem was finally proven by Richard Schoen and Shing-Tung Yau in 1979, who made an additional technical assumption about the nature of the stress–energy tensor. The original proof is very difficult; Edward Witten soon presented a much shorter "physicist's proof", which has been justified by mathematicians—using further very difficult arguments. Roger Penrose and others have also offered alternative arguments for variants of the original positive energy theorem.

Examples[edit]

Noteworthy examples of vacuum solutions, electrovacuum solutions, and so forth, are listed in specialized articles (see below). These solutions contain at most one contribution to the energy–momentum tensor, due to a specific kind of matter or field. However, there are some notable exact solutions which contain two or three contributions, including:

NUT-Kerr–Newman–de Sitter solution contains contributions from an electromagnetic field and a positive vacuum energy, as well as a kind of vacuum perturbation of the Kerr vacuum which is specified by the so-called NUT parameter,
Gödel dust contains contributions from a pressureless perfect fluid (dust) and from a positive vacuum energy.

Some hypothetical possibilities which don't fit into our rough classification are:

certain wormhole metrics (which can serve as a speculative toy model of a stargate held open by a hypothetical kind of exotic matter, as in 2001: A Space Odyssey; also a toy model of hypothetical time machine, see below),
Alcubierre metric (which has been used as a speculative toy model of effectively superluminal space travel, as in the warp drive from Star Trek).
"Time machines", i.e. initially nice spacetimes in which at some stage of evolution closed causal curves appear.

Some doubt has been cast upon whether sufficient quantity of exotic matter needed for wormholes and Alcubierre bubbles can exist.^[3] Later, however, these doubts were shown^[4] to be mostly groundless. The third of these examples, in particular, is an instructive example of the procedure mentioned above for turning any Lorentzian manifold into a "solution". It is along this way that Hawking succeeded in proving^[5] that time machines of a certain type (those with a "compactly generated Cauchy horizon") cannot appear without exotic matter. Such spacetimes are also a good illustration of the fact that unless a spacetime is especially

phymath999