拉普拉斯对噪声敏感，会产生双边效果。不能检测出边的方向

边缘检测：Sobel、拉普拉斯算子

分类： 【OpenCV】 2012-08-04 13:41 6440人阅读 评论(22) 收藏 举报

borderdstimagec

目录(?)[+]

1. 边缘
2. 一阶导数法梯度算子
1. 梯度算子 Gradient operators
2. Sobel算子
1. 相关代码
3. 二阶微分法拉普拉斯
1. LapLace 拉普拉斯算子
1. 相关代码
4. 实践效果
1. Sobel 边缘检测
2. Laplace边缘检测
4. 转载请注明出处httpblogcsdnnetxiaowei_cquarticledetails7829481
5. 实验代码下载httpdownloadcsdnnetdetailxiaowei_cqu4475976

边缘

边缘(edge)是指图像局部强度变化最显著的部分。主要存在于目标与目标、目标与背景、区域与区域(包括不同色彩)之间，是图像分割、纹理特征和形状特征等图像分析的重要基础。
图像强度的显著变化可分为：

• 阶跃变化函数，即图像强度在不连续处的两边的像素灰度值有着显著的差异；
• 线条（屋顶）变化函数，即图像强度突然从一个值变化到另一个值，保持一较小行程后又回到原来的值。

图像的边缘有方向和幅度两个属性,沿边缘方向像素变化平缓,垂直于边缘方向像素变化剧烈.边缘上的这种变化可以用微分算子检测出来,通常用一阶或二阶导数来检测边缘。

（a）（b）分别是阶跃函数和屋顶函数的二维图像；（c）（d）是阶跃和屋顶函数的函数图象；（e）（f）对应一阶倒数；（g）（h）是二阶倒数。

一阶导数法：梯度算子

对于左图，左侧的边是正的（由暗到亮），右侧的边是负的（由亮到暗）。对于右图，结论相反。常数部分为零。用来检测边是否存在。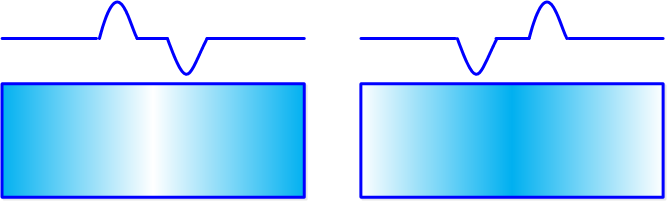

梯度算子 Gradient operators

函数f(x,y)在(x,y)处的梯度为一个向量：

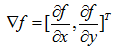
计算这个向量的大小为：

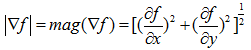
近似为:

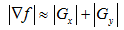
梯度的方向角为：

 

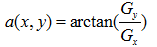
Sobel算子

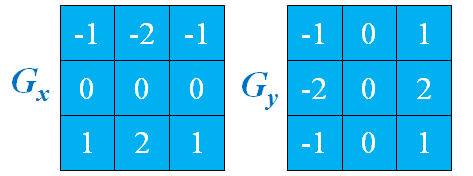
sobel算子的表示：

 

梯度幅值：

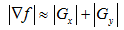
用卷积模板来实现：

【相关代码】

接口

[cpp] view plaincopyprint?

1. CV_EXPORTS_W void Sobel( InputArray src, OutputArray dst, int ddepth,  
2.                          int dx, int dy, int ksize=3,  
3.                          double scale=1, double delta=0,  
4.                          int borderType=BORDER_DEFAULT );  

CV_EXPORTS_W void Sobel( InputArray src, OutputArray dst, int ddepth,
                         int dx, int dy, int ksize=3,
                         double scale=1, double delta=0,
                         int borderType=BORDER_DEFAULT );

使用

[cpp] view plaincopyprint?

1. /////////////////////////// Sobe l////////////////////////////////////  
2. /// Generate grad_x and grad_y  
3. Mat grad_x, grad_y;  
4. Mat abs_grad_x, abs_grad_y;  
5. /// Gradient X  
6. //Scharr( src_gray, grad_x, ddepth, 1, 0, scale, delta, BORDER_DEFAULT );  
7. //Calculates the first, second, third, or mixed image derivatives using an extended Sobel operator.  
8. Sobel( src_gray, grad_x, ddepth, 1, 0, 3, scale, delta, BORDER_DEFAULT );     
9. convertScaleAbs( grad_x, abs_grad_x );  
10. /// Gradient Y    
11. //Scharr( src_gray, grad_y, ddepth, 0, 1, scale, delta, BORDER_DEFAULT );  
12. Sobel( src_gray, grad_y, ddepth, 0, 1, 3, scale, delta, BORDER_DEFAULT );     
13. convertScaleAbs( grad_y, abs_grad_y );  
14. /// Total Gradient (approximate)  
15. addWeighted( abs_grad_x, 0.5, abs_grad_y, 0.5, 0, grad );  

  /////////////////////////// Sobe l////////////////////////////////////
  /// Generate grad_x and grad_y
  Mat grad_x, grad_y;
  Mat abs_grad_x, abs_grad_y;
  /// Gradient X
  //Scharr( src_gray, grad_x, ddepth, 1, 0, scale, delta, BORDER_DEFAULT );
  //Calculates the first, second, third, or mixed image derivatives using an extended Sobel operator.
  Sobel( src_gray, grad_x, ddepth, 1, 0, 3, scale, delta, BORDER_DEFAULT );   
  convertScaleAbs( grad_x, abs_grad_x );
  /// Gradient Y  
  //Scharr( src_gray, grad_y, ddepth, 0, 1, scale, delta, BORDER_DEFAULT );
  Sobel( src_gray, grad_y, ddepth, 0, 1, 3, scale, delta, BORDER_DEFAULT );   
  convertScaleAbs( grad_y, abs_grad_y );
  /// Total Gradient (approximate)
  addWeighted( abs_grad_x, 0.5, abs_grad_y, 0.5, 0, grad );

二阶微分法：拉普拉斯

二阶微分在亮的一边是负的，在暗的一边是正的。常数部分为零。可以用来确定边的准确位置，以及像素在亮的一侧还是暗的一侧。

LapLace 拉普拉斯算子

二维函数f(x,y)的拉普拉斯是一个二阶的微分，定义为：

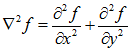
其中：

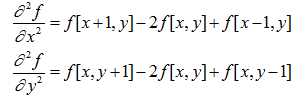
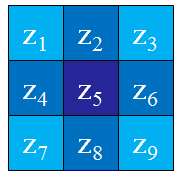
可以用多种方式将其表示为数字形式。对于一个3*3的区域，经验上被推荐最多的形式是：

定义数字形式的拉普拉斯要求系数之和必为0

 

【相关代码】

接口

[cpp] view plaincopyprint?

1. CV_EXPORTS_W void Laplacian( InputArray src, OutputArray dst, int ddepth,  
2.                              int ksize=1, double scale=1, double delta=0,  
3.                              int borderType=BORDER_DEFAULT );  

CV_EXPORTS_W void Laplacian( InputArray src, OutputArray dst, int ddepth,
                             int ksize=1, double scale=1, double delta=0,
                             int borderType=BORDER_DEFAULT );

使用

[cpp] view plaincopyprint?

1. Mat abs_dst,dst;  
2.   int scale = 1;  
3.   int delta = 0;  
4.   int ddepth = CV_16S;  
5.   int kernel_size = 3;   
6.   Laplacian( src_gray, dst, ddepth, kernel_size, scale, delta, BORDER_DEFAULT );  
7.   convertScaleAbs( dst, abs_dst );  
8.   namedWindow( window_name2, CV_WINDOW_AUTOSIZE );  

Mat abs_dst,dst;
  int scale = 1;
  int delta = 0;
  int ddepth = CV_16S;
  int kernel_size = 3; 
  Laplacian( src_gray, dst, ddepth, kernel_size, scale, delta, BORDER_DEFAULT );
  convertScaleAbs( dst, abs_dst );
  namedWindow( window_name2, CV_WINDOW_AUTOSIZE );

实践效果

原图

注意，边缘检测对噪声比较敏感，需要先用高斯滤波器对图像进行平滑。参考博文：【OpenCV】邻域滤波：方框、高斯、中值、双边滤波

Sobel 边缘检测

Sobel算子可以直接计算Gx 、Gy可以检测到边的存在，以及从暗到亮，从亮到暗的变化。仅计算| Gx |，产生最强的响应是正交 于x轴的边； | Gy |则是正交于y轴的边。

 

Laplace边缘检测

拉普拉斯对噪声敏感，会产生双边效果。不能检测出边的方向。通常不直接用于边的检测，只起辅助的角色，检测一个像素是在边的亮的一边还是暗的一边利用零跨越，确定边的位置。

转载请注明出处：http://blog.csdn.net/xiaowei_cqu/article/details/7829481

实验代码下载：http://download.csdn.net/detail/xiaowei_cqu/4475976