朗道提出了序参量的概念对连续相变提供了一个统一的描述,认为连续相变的特征是物质有序程度
的改变及与之相伴的物质对称性的改变,通常在临界温度以下的相,对称性低、有序度高、序参量非零,
临界点以上的相,对称性较高、有序度较低、序参量为零,随着温度的降低,序参量在临界点连续地从零
变到非零。
http://media.open.com.cn/media_file/rm/dongshi2004/rlxywltj/T02/jiaxue/chapter3/chapter3-9-4.htm


| | 朗道提出了序参量的概念对连续相变提供了一个统一的描述,认为连续相变的特征是物质有序程度
的改变及与之相伴的物质对称性的改变,通常在临界温度以下的相,对称性低、有序度高、序参量非零,
临界点以上的相,对称性较高、有序度较低、序参量为零,随着温度的降低,序参量在临界点连续地从零
变到非零。
|
|
|
| |
1. 单轴各向异性铁磁体
自旋取向只能沿着一个方向(正或负)序参量的能数为 1 。
2. 单轴各向异性铁磁体的能量
两个相邻原子在其磁矩平行时有较低的能量。
a. 基态,绝对零度  能量最低,原子号为固有磁矩,所有原子磁矩取向相同,完全有序。
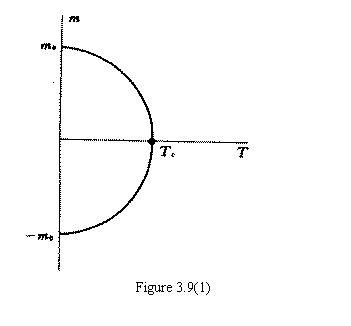
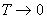 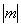 最大, m= ± m o
b. 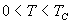
热运动有减弱有序取向的趋势 
c. 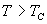 时
自发磁化强度为零,物质转变为顺磁状态。
3. 对称性破缺
在 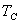 以上没有自发磁化,上下两个方向是对称的或等价的。 当温度变到居里点以下,这两个方向就不
对称了,这是一种对称性 “ 破缺 ” 。
4. 序参量
自发磁化强度 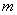 是一个标量,正号对应磁矩朝上,负号对应磁矩朝下。
5. 与普通流体二级相变对应
m 对应于 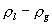  是标量,维数是 1 。顺磁相 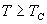 ,对应于液气不分。磁化强度朝上、
朝下分别对应于气态和液态。
|
|
|
| |
一般来说,序参量可以有 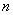 维,如果序参量要在 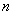 维空间中描述,我们就说序参量是 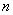 维的。
设:只有二个量决定体系的临界行为,即空间维数 d 和序参量维数 n ,具有相同的 d 和 n 的体系属
于同一个普适类,它们有相同的临界指数,相同的临界行为。
例如,普通流体(气 — 液)为变系,单轴各有异性铁磁体,属于同一普适类, 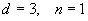 ,
超导、超流、相变,序参量是 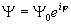 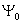 , , 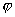 决定, 决定, 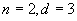 ,和三维 ,和三维 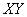 模型属于同一普适类。 模型属于同一普适类。
|
|
|
| |
对于序参量维数为 1 的系统,下面的讨论完全适用,对于序参量维数大于 1 的系统,则要稍
作修改。
1. 磁化强度
对于铁磁体,自由能是温度和磁化强度的函数
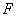 = =  当 当 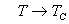 时 把自由能在 时 把自由能在 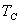 附近展开 附近展开
由于 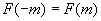 ,在稳定平衡状态, 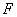 具有最小值,应有:
由  可推出 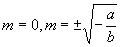
即,在 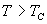 时, 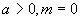 。
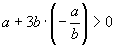 ,
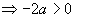 即 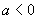 。
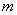 在  处连续地由零转变为非零,所以在 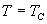 应有 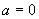 ,所以最简单的假设是令:
和 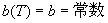 。
由  是实数,可知, 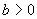 。
因此,单轴铁磁体的磁化强度为:
 , 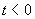
与  ,比较
可得 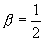 。
2. 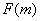 曲线
在临界点以上
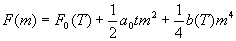  。
曲线如图 3.9 (1)
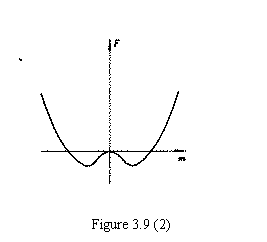
在临界点以下
曲线如图 3.9 (2)
3. 铁磁体的零场比热
由 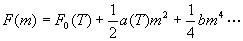
和平衡时:  可知,
当系统处于是平衡态时:
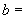 常数 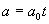
利用公式 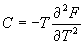 ,
在 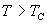 时:
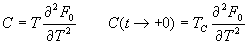 。
 在  时:
即 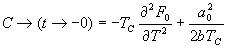
上式表明,有序相的比热大于无序相的比热,且在 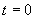 外比热的突变是有限的。
由于有  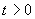
4. 磁化率的突变
在存在外场时,吉布斯函数  为:
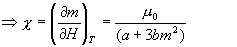 代入 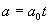 可得
与 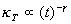 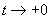
比较可知, 
和 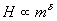 对比可知, 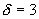 。
6. 结论
朗道连续相变理论,写出了描述铁磁体临界行为方程:
得到临界指数:
朗道理论得到的临界指数与实验结果之间存在差异,主要原因它只研究平均值的变化规矩,没有考虑
涨落。但理论图象简单、清晰,在一定程度上反应了事物的本质,所以具有很大的价值。
 |
|
|
|
|



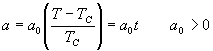
 是实数,可知,
是实数,可知,  ,
, 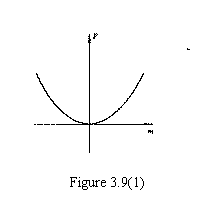
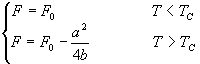
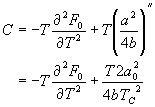
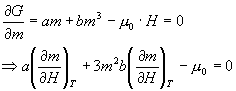
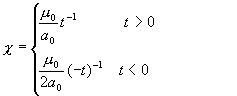
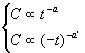
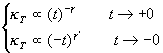
No comments:
Post a Comment