请帮我解释一个lagrangian中的一项

smug · 发表于 2009-7-11 08:43:32

Ryder的QFT里推导SSB的时候(P293)，引入非零的VEV后，给了一个lagrangian，其中有一项为 $A^{\mu}\partial_{\mu}\phi_2$ , 相应的解释为
which would seem to indicate that a propagating photon could turn into a $\phi_2$ field, so $\phi_2$ does not seem to be a very physical field. In fact, it can be eliminated by a gauge transformation.

问题
1>"a propagating photon could turn into a $\phi_2$ field"这个结论是如何得到的？
2>"so $\phi_2$ does not seem to be a very physical field"为什么要用very,难道可以说 $\phi_2$ 是60％的physical field?
3>这时的lagrangian里photon(guage boson $A_{\mu}$ )已经有质量了，因而已经破坏了"gauge symmetry". 为什么还要说"it can be eliminated by a gauge transformation"？
4>这个如何解释 $(\partial_{\mu}\phi_2)A^{\mu}$ ?
5>这个, $(\partial_{\mu}\phi) A^{\mu}\phi$ ,也有明确的物理意义吗?

thx

[ 本帖最后由 smug 于 2009-7-11 01:58 编辑 ]

smug · 发表于 2009-7-11 11:26:15

我好像犯了个错误.继续思考中...........

sage · 发表于 2009-7-11 13:10:24

1) With this term, there is vertex which turns a A into a phi.

2) That's a vague statement. Usually, we start by considering a collection independent fields, i.e., no terms like the one you mention. The term you write can be eliminated by a change of basis, or gauge transformation.

3) In SSB, the gauge symmetry is not broken by the Lagrangian (it is only broken by the ground state of the Lagrangian). You can still perform gauge transformation of the Lagrangian, the result won't change physical observables.

And, by the way, if you are serious about quantum field theory, do not read Ryder.

wpzhou · 发表于 2009-7-11 13:38:59

一直理解这个phi为矢量场的纵向分量

sage · 发表于 2009-7-12 01:59:05

It is the eaten Goldstone, which becomes the longitudinal mode of the massive gauge boson.

vasin · 发表于 2009-7-12 14:09:31

其实你的误解来自于人们对"broken“这一词的不恰当使用。我猜你说的是spontaneous broken标量电动力学，在这个理论中，规范对称性从来没有被"broken"过，它仍然是一个严格对称性。'unbroken"和”broken“的区别是，前者reduce gauge redundancy in the same vacumn, while latter reduce gauge redundancy in different vacumn. 这是我们可以对真空期待值作规范旋转的原因。

星空浩淼 · 发表于 2009-7-12 17:41:31

专业人士回答问题更准确可信，但有时也容易把简单问题回答得复杂化了。我试图对楼主问题提供更简单易懂的回答（不对的地方请sage兄等纠正）：

1）电磁场的场算子与标量场的场算子中，都含有各自的产生算符和湮灭算符，因此在微扰计算的展开中，你说的这一项对S矩阵的贡献中，含有“湮灭一个光子而产生一个标量粒子”和“湮灭一个标量粒子而产生一个光子”的过程，因此书上才有此说。

2）也许这是因为（与你的问题1对应），作为矢量粒子的光子，不能与单个的标量粒子直接相互转化，或者说，实验上没有发现质量为零的光子变成质量为零的标量粒子的过程，因此这里就判定Φ2场不应该不存在。

3）显然，楼主把"it can be eliminated by a gauge transformation"中的"it"理解错了，文章中说的"it"是现实中不应该存在的Φ2场（以及问题1中的那一项），它可以用过规范变换去掉（因而没有物理意义，这样也恰好可以对应你的问题1）和2）。

4）这一项可以看作是电磁场与Φ2场之间的一个相互作用项。按照书上说的，该项可以通过规范变换消除了，因而不代表有物理意义的项。

5）这一项，与一个光子和两个标量粒子之间的相互作用（相互转换）有关吧。一个光子不能变成一个标量粒子（因此上述包含Φ2场的项不应该不存在），但是变成两个标量粒子的过程，是可以存在的吧。都是在树图近似下谈论的。

[ 本帖最后由星空浩淼于 2009-7-12 17:43 编辑 ]

smug · 发表于 2009-7-12 22:53:10

谢谢各位。

我把后面的内容看了，加上诸位的解释，发现自己那时疏忽了一些东西。

这个“问题”是出自spontaneous breaking of gauge symmetry (Abelian case).
所以 $\phi_2$ 是对应global gauge里的massless Goldstone boson，在local symmetry里消失掉了

这里的“eliminated by a gauge transformation”指的是选一个特殊的gauge，使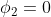 $\phi_2=0$

Zee 在书里写的
In this sense, gauge invariance is, strictly speaking, not a "real" symmetry but merely a reflection of teh fact that we used a redundant description: a Lorentz vector field to describe two physical degrees of freedom.

[ 本帖最后由 smug 于 2009-7-12 15:56 编辑 ]

smug · 发表于 2009-7-12 22:55:21

原帖由 星空浩淼
这一项，与一个光子和两个标量粒子之间的相互作用（相互转换）有关吧。一个光子不能变成一个标量粒子（因此上述包含Φ2场的项不应该不存在），但是变成两个标量粒子的过程，是可以存在的吧。都是在树图近似下谈论的。

按你的说法， $(\partial\phi^*)A\phi$ 和 $\phi^*A\phi$ 的区别是什么？

另外， local gauge的情况，可以在一部分“空间”里选一种gauge，在另外的里选另一种吗？

[ 本帖最后由 smug 于 2009-7-12 16:10 编辑 ]

星空浩淼 · 发表于 2009-7-13 01:04:05

我写公式不容易，就用“前一项”和“后一项”指代你楼上的两个公式。我明白你的意思：你是说，既然后一项在树图近似下通常直接与一个光子和两个标量粒子之间的相互作用有关，而前一项中好歹多了一个求微分运算，总得跟后一项有所不同吧。我觉得二者的差别之一是（微扰近似下）：前一项中多了一个求微分运算，相当于多乘以一个四动量（量纲为1），并且对于被求微分的场算子，它原来表达成正能项与负能项之和，求微分之后变成正能项与负能项之差。后一项不乘这个四动量，但需要多乘以一个量纲为1的耦合系数。前一项的耦合系数量纲为0，后一项的耦合系数量纲为1，重整化时二者有不同的表现吧。

你的第二个问题我没有看明白。

[ 本帖最后由星空浩淼于 2009-7-13 01:15 编辑 ]

smug · 发表于 2009-7-13 01:52:13

原帖由 星空浩淼 于 2009-7-12 18:04 发表
我写公式不容易，就用“前一项”和“后一项”指代你楼上的两个公式。我明白你的意思：你是说，既然后一项在树图近似下通常直接与一个光子和两个标量粒子之间的相互作用有关，而前一项中好歹多了一个求微分运算，总得跟后一项有 ...

谢谢。你解释的部分我明白了，可是我还是卡在我的问题那。 2者的“物理意义”或者说所表示的“物理过程”有何不同（后者我知道）？

第2个问题：用unitary gauge可以让 $\phi_2=0$ , 但也可以选别的gauge，虽然 $\phi_2\neq 0$ . 通常x是作为变量的，可不可以这样，当x<0时用unitary gauge，当x>0是用landau gauge？

[ 本帖最后由 smug 于 2009-7-13 03:02 编辑 ]

星空浩淼 · 发表于 2009-7-13 10:08:28

在Φ场的局域规范变换中Φ→exp[iΛ(x)]Φ，变换参数Λ(x)与时空坐标x有关。如果仅仅通过不同x处的不同Λ选择，仅仅通过群参数Λ的不同选择，就可以达到x<0时对应unitary gauge、当x>0对应landau gauge的效果，那你说的当然可以。不过，变换参数Λ(x)是连续函数，在无穷小规范变换下Φ→[1+iΛ(x)]Φ，Λ(x)是无穷下量，在x=0的领域内，Λ(x)的变化是否可以使得规范从unitary gauge变化到landau gauge，这个需要判断一下。即：这是使得Λ(x)在x=0处产生突变还是保持连续变化？如果是突变，就不行。

vasin · 发表于 2009-7-13 10:24:44

原帖由 smug 于 2009-7-12 22:55 发表

按你的说法，(\partial\phi^*)A\phi和\phi^*A\phi的区别是什么？

另外， local gauge的情况，可以在一部分“空间”里选一种gauge，在另外的里选另一种吗？

Such term $\phi^*A\phi$ do not exist.

星空浩淼 · 发表于 2009-7-13 10:54:49

原帖由 vasin 于 2009-7-13 10:24 发表
Such term \phi^*A\phi do not exist.

呵呵，的确如此，我前面没有注意到这点。在标量QED中，相互作用项里面包含两个A的缩并与Φ^*Φ的乘积，整体上是一个Lorentz标量（耦合系数是无量纲的），而楼主提到的Φ^*AΦ不是Lorentz标量，可能还会破坏规范对称性。

可能楼主从协变微分表达的项中提取相互作用项时，弄掉了一个A

[ 本帖最后由星空浩淼于 2009-7-13 11:38 编辑 ]

smug · 发表于 2009-7-13 13:05:18

原帖由 星空浩淼 于 2009-7-13 03:54 发表

呵呵，的确如此，我前面没有注意到这点。在标量QED中，相互作用项里面包含两个A的缩并与Φ^*Φ的乘积，整体上是一个Lorentz标量（耦合系数是无量纲的），而楼主提到的Φ^*AΦ不是Lorentz标量，可能还会破坏规范对称性。
可能楼主从 ...

谢谢。是我疏忽了，不是漏了个A，是把这个看成是2个fermi 场夹一个boson场。那个Φ应该是virtual particle，不能在initial和final态出现。（希望这次没解释错）

我主要是对“求微分”的那部分是什么物理过程来解释不清楚。

sage · 发表于 2009-7-13 13:38:42

Yes. The fact that there is a term of the form d \phi A means that phi is a Goldstone.

And Zee is certainly right.

To 14#:

\phi A \phi does not exist not just because it is not Lorentz invariant.
A^2 \phi^2 does not exist either if phi is Goldstone. A Goldstone boson can only have derivative couplings.

15#:
No, phi is not a virtual particle. A field in Lagrangian can have excitations which either virtual or real. Phi is the longitudinal mode of the Gauge boson. Thinking about a massive gauge boson with 3 polarizations, and thinking about a massive gauge boson with two polarizations, with additional scalar are the same description (differ by a gauge choice).

smug · 发表于 2009-7-13 13:51:37

原帖由 sage 于 2009-7-13 06:38 发表
Yes. The fact that there is a term of the form d \phi A means that phi is a Goldstone.

And Zee is certainly right.

To 14#:

\phi A \phi does not exist not just because it is not Lorentz invariant ...

" A Goldstone boson can only have derivative couplings."为什么呢？有了derivative couplings的Goldstone boson有什么特殊的地方吗？

[ 本帖最后由 smug 于 2009-7-13 06:53 编辑 ]

sage · 发表于 2009-7-13 14:04:25

With derivative couplings only, you can prove it is exactly massless. If not, you will generate a mass for it.

smug · 发表于 2009-7-13 14:09:22

原帖由 sage 于 2009-7-13 07:04 发表
With derivative couplings only, you can prove it is exactly massless. If not, you will generate a mass for it.

谢谢。

PS：这个过程用latex怎么写？

PPS:在collider里搞EWSB或new physics的时候，为什么要“measure”resonances？

[ 本帖最后由 smug 于 2009-7-13 08:44 编辑 ]

六根胡须 · 发表于 2009-7-14 02:56:44

1）Globle symmetry 自发破缺
Goldstone场是：真空凝聚所破坏的Globle对称性生成元“作用”方向的自由度的定域化经典场表示（粗略地说就是切向的自由度定域化后的场表示，不要问我是否存在这种表示，这可能是个很难以证明的结论）。

如果这一自由度是空间均匀受激发的，那么我们将无法感受到其存在。因为理论原本的对称性保证了无论破缺至哪一个方向，真空都没有改变。因此在一个整合了Goldstone场和其余常规场的有效拉氏量里只可能出现Sage兄所言的微商耦合项。

形象地说，只有凝聚体在局部发生方向变化时才可能被生活在凝聚体中的人所观测到（和常规粒子发生作用），如果整个凝聚体在转动，对于身在其中的人而言是无法观测的（无法和常规粒子发生耦合）。（注意：Goldstone不是凝聚本身，而是凝聚的变化，而且是局部变化）
2）Gauge symmetry 自发破缺
前面说到了Goldstone粒子是一种整体对称性破缺后导致的局部激发。可是当这种对称性本身还有定域性时，问题自然产生了：如果某种看似局域的激发，仅仅是某个规范变换导致的，那么这样的激发同样不具备观测效应。因此，要把握住真实的物理效应，我们必须着手消除规范自由度。具体问题中，例如我们所讨论的例子中的unitary规范，它把\phi场消灭掉。但这并没有消灭Goldstone，而是把那些假的（重复的）“Goldstone”激发模式给消除了。真实的Goldstone效应表现为规范粒子的纵向激发，这种激发是有确切的物理贡献的，这种物理贡献当然也不依赖于你到底选择何种规范。

[ 本帖最后由六根胡须于 2009-7-14 03:02 编辑 ]

phymath999

Saturday, December 21, 2013

回复 1# 的帖子

请帮我解释一个lagrangian中的一项

相关帖子

回复 1# 的帖子

回复 4# 的帖子

回复 1# 的帖子

回复 9# 的帖子

回复 11# 的帖子

回复 8# 的帖子

回复 17# 的帖子

评分

浏览过的版块

No comments:

Post a Comment