二维相位去包裹:路径积分法
发表于 07 April 2013
二维相位去包裹:路径积分法
本文介绍几种基于路径积分的二维相位展开方法。这只是个预告,表示这几天没有闲着。为什么二维相位展开会发生问题?
Itoh’s算法的二维扩展
Itoh’s一维相位展开算法很容易扩展到二维。我们可以先对第一列进行解包裹,然后在此基础上对每行进行解包裹,整个相位图像就都能被解包裹了。
我把扩展的itoh’s算法函数写在util中并导入
from util import *
from mpl_toolkits.mplot3d import axes3d
X, Y, Z = axes3d.get_test_data(0.05)
Z_origin = Z.copy()
plt.figsize(10,10)
plt.subplot(121)
plt.title("origin phase")
plt.imshow(Z, cmap='gray')
ax = plt.gca()
ax.set_axis_off()
colorbar(shrink=.40)
plt.subplot(122)
plt.title("wraped phase")
ax = plt.gca()
ax.set_axis_off()
Z = wrap(Z)
plt.imshow(Z, cmap='gray')
colorbar(shrink=.40)
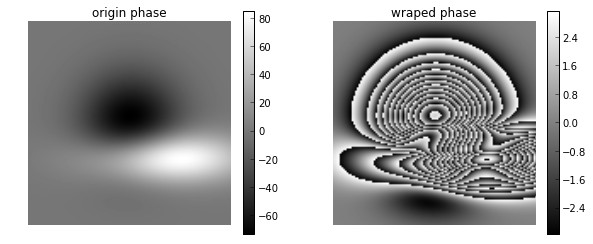
紧接着用itoh的方法解包裹
Z = raster_unwrap2(Z)
plt.figsize(10,10)
plt.subplot(121)
ax = plt.gca()
ax.set_axis_off()
plt.title("unwraped phase")
plt.imshow(Z, cmap='gray')
colorbar(shrink=.40)
plt.subplot(122)
ax = plt.gca()
ax.set_axis_off()
plt.title("erro map")
plt.imshow(Z - Z_origin, cmap='gray')
colorbar(shrink=.40, ticks=None)
np.all(np.abs((Z - Z_origin) < 1e-8))

正如我们所见,这算法效果很好。但是如果数据点出了点问题的话……
Z = wrap(Z)
x = np.random.randint(0,120,100)
y = np.random.randint(0,120,100)
Z[x,y] = random.random() * 3
plt.subplot(131)
ax = plt.gca()
ax.set_axis_off()
plt.title("noisy wraped phase")
plt.imshow(Z, cmap='gray')
colorbar(shrink=.25)
Z = raster_unwrap2(Z)
plt.subplot(132)
plt.title("noisy unwraped phase")
ax = plt.gca()
ax.set_axis_off()
plt.imshow(Z, cmap='gray')
colorbar(shrink=.25)
np.all((Z == Z_origin))
plt.subplot(133)
plt.imshow(Z-Z_origin, cmap='gray')
ax = plt.gca()
ax.set_axis_off()
plt.title("error map")
colorbar(shrink=.25)

我加了一些随机噪声,结果就悲剧了。查看误差图给我们了一些启示。在某些出问题的点同一行又边全都出了问题。这种解包裹误差不断扩大并形成一条线的现象,似乎 叫做 拉线 现象(我瞎说的,只是有文献提到过拉线现象,也可能就是这个吧……)。
如果我们对Itoh算法换一种方式扩展。先对第一行解包裹,再在此基础上对各个列解包裹。如果没有有问题的点。结果和第一种扩展方式一样。这给我们个启示,我们可以在任意方向进行相位去包裹,但只要碰到出问题的点都会在之后的积分路径中出现问题。
如果要解包裹出正确的相位,必须绕过这些奇点(有问题的点)。
事实上,相位解包裹领域借用了高等数学和复变函数分析里的理论和观点,并最终形成了相位解包裹问题的留数定理。
相位去包裹留数定理
要想解包裹与路径无关,必须有:
在数字图像中,最小的环路是2X2大小的四个像素,如下图所示。通过计算∑ 4 i=1 Δ i 是否为零,为零则无留数,否则此区域内有正或负留数。实际上,这些有问题的点留数通常不会为0。
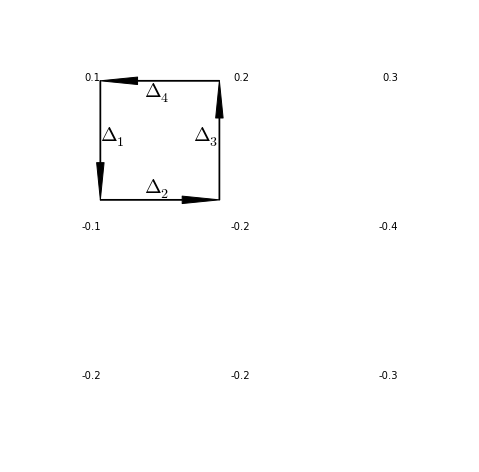
为了在任意方向上能进行正确的解包裹,必须想办法使环路内的留数和为0,让积分路径(也是解包裹的路径)绕过这些留数不为0的奇点。
之后所提到的,我所看到的一些路径积分方法。都是通过尽量在可靠的地方进行相位展开(即积分),想办法绕开可能造成问题的点,或平衡这些造成问题的点。
之后做好准备看看那些大牛们发展出的各种路径积分算法吧。我已经佩服的五体投地了。这复杂程度已经让个人Keep it simple, stupid的人生哲学彻底崩坏。各路人马的算法涉及大量数学理论、信号处理理论(mask、noise filter、quality map)、图形形态学操作(开闭操作、连通性判断)、图论(分支切割算法)、最小生成树……完全看跪了……如果你准备动手实践,为了提高时间和空间效率,还有涉及可能是算法设计的东西吧1。
几种路径积分算法
Goldstein 分支切割(branch cut)算法
该算法旨在用最短的路径平衡正负留数,设置解包裹时的障碍,使解包裹路径能按照正确的方向进行。总体上说,该算法相当高效,很容易查看效果。但跟质量图没关系,很容易错误的放置障碍,导致错误的积分路径。质量引导(quality-guided)算法
先积分质量高的地方,后积分质量低的地方,这基本能保证解包裹路径的正确。这个算法和留数没关系,所以不能保证不出错。但如果有个非常好的质量图,结果相当棒。另外,效率也不错。掩码分支(mask)算法
前两种算法的杂交,通过某种方法沿着质量最低的地方扩展mask,最后解包裹时绕过这些mask。同上方法,没有好的质量图就别去试。flynn最小断点算法
很直观的算法。就是把不连续的部分通过增加整数倍个2π 变得连续,虽然说起来没这么简单。该算法用了个生成树,效果很好,还可以用质量图获得更好的效果……
No comments:
Post a Comment