作者:袁士霄 时间:2010-07-22 01:26:03
纠正一个错误:“作者:袁士霄 回复日期:2010-07-18 13:28:21在波动的语言里,波矢的绝对值可以很小很小,但是不能为零。这与经典力学允许粒子静止不动是冲突的。”。波矢作为自由粒子波的表征,与普通的三维矢量有同样的变换规则,可以在某个参照系中取值为0。
作者:bellbasis 回复日期:2010-07-21 16:09:31
静止的唯一定义是动量为0~ 我没有限定不能实用 delta(x),我只是说delta(x)不是静止粒子而已。
************
由于测不准原理的限制,“静止”这个说法本不应该出现在量子理论中。为了与经典力学相对照,我想到量子力学中与之相对应的两种情形,我们对它们真是含义没有什么分歧。
作者:圆周率谐音 回复日期:2010-07-21 20:52:07
在经典中的静止概念让在量子力学p=0时,而位置不确定,就这样,给一笔勾销了么.
**********************
没有勾销哇,波函数的空间部分是ψ(x) = 1,与其它自由粒子波一样,每一处的几率幅相同。也就是,不像经典力学那样,粒子不再限定在一个固定的位置上。
在量子力学中,被限定固定位置上的粒子,不再是自由粒子。
<"实际上,量子力学有3个解释,薛定谔方程,矩阵力学,路径积分。>
那么量子场论是属于那个里的呢,是属于矩阵力学,还是根本就不算数呢?并由此设想的真空虚粒子,以及基态和激发态不算量子解释了吗?若希格斯波色子不存在(非因检测不到),粒子质量的产生就没法解释了么,虚粒子加工厂是否就因而破产了呢.我想若爱因斯坦在世,他照样还像抛弃以太那样,非闹翻天不可.二位高手怎么看?
量子力学的三种表达形式,波动力学、矩阵力学和路径积分彼此等价,前二者通过希尔伯特空间的表象变换相关联。路径积分则表达了一种新的概率逻辑规则——费曼规则,以取代老的贝叶斯概率规则,
关于量子场论说来就话长了,引用前面一段:“在量子场论看来,时空中分布着各种各样的场,每一种场的最低能态是真空态,场的激发导致粒子的产生,场的退激发导致粒子湮灭。因此,波场是粒子的本源,从而也是物质的本源;而物质是场的一种表现。波场可以表现得没有实粒子,比如真空态。”在量子场论中,基态和激发态是场方程的一连串解,一种是演绎结果,而不是一种解释。
希格斯玻色场的引入使优美的,但不符合实际的规范场论理论获得生命力。由此打开了经由对称性通往统一场理论路径。如果没有希格斯波色场,规范思想下建立起来的,并且已经为多项实验验证了的弱电统一理论、量子色动力学和标准模型都不再成立。至于爱因斯坦怎么想,还是不猜测的好。我们只要铭记,20世纪物理学的各个分支都或多或少发源于斯,也可能是方法上的借鉴。
袁士霄你说<波矢频谱马上就变得极其分散,>是不是根据科学界对孤波子一类研究得出一致性结论的一种对应?
我是针对定位粒子说的,量子力学中的定位粒子的状态是各种自由波的叠加。对于粒子,我们只要关心它的诸多参数和统计特性,这就够了。
作者:bellbasis 回复日期:2010-07-21 16:09:31
静止的唯一定义是动量为0~ 我没有限定不能实用 delta(x),我只是说delta(x)不是静止粒子而已。
************
由于测不准原理的限制,“静止”这个说法本不应该出现在量子理论中。为了与经典力学相对照,我想到量子力学中与之相对应的两种情形,我们对它们真是含义没有什么分歧。
作者:圆周率谐音 回复日期:2010-07-21 20:52:07
在经典中的静止概念让在量子力学p=0时,而位置不确定,就这样,给一笔勾销了么.
**********************
没有勾销哇,波函数的空间部分是ψ(x) = 1,与其它自由粒子波一样,每一处的几率幅相同。也就是,不像经典力学那样,粒子不再限定在一个固定的位置上。
在量子力学中,被限定固定位置上的粒子,不再是自由粒子。
<"实际上,量子力学有3个解释,薛定谔方程,矩阵力学,路径积分。>
那么量子场论是属于那个里的呢,是属于矩阵力学,还是根本就不算数呢?并由此设想的真空虚粒子,以及基态和激发态不算量子解释了吗?若希格斯波色子不存在(非因检测不到),粒子质量的产生就没法解释了么,虚粒子加工厂是否就因而破产了呢.我想若爱因斯坦在世,他照样还像抛弃以太那样,非闹翻天不可.二位高手怎么看?
量子力学的三种表达形式,波动力学、矩阵力学和路径积分彼此等价,前二者通过希尔伯特空间的表象变换相关联。路径积分则表达了一种新的概率逻辑规则——费曼规则,以取代老的贝叶斯概率规则,
关于量子场论说来就话长了,引用前面一段:“在量子场论看来,时空中分布着各种各样的场,每一种场的最低能态是真空态,场的激发导致粒子的产生,场的退激发导致粒子湮灭。因此,波场是粒子的本源,从而也是物质的本源;而物质是场的一种表现。波场可以表现得没有实粒子,比如真空态。”在量子场论中,基态和激发态是场方程的一连串解,一种是演绎结果,而不是一种解释。
希格斯玻色场的引入使优美的,但不符合实际的规范场论理论获得生命力。由此打开了经由对称性通往统一场理论路径。如果没有希格斯波色场,规范思想下建立起来的,并且已经为多项实验验证了的弱电统一理论、量子色动力学和标准模型都不再成立。至于爱因斯坦怎么想,还是不猜测的好。我们只要铭记,20世纪物理学的各个分支都或多或少发源于斯,也可能是方法上的借鉴。
袁士霄你说<波矢频谱马上就变得极其分散,>是不是根据科学界对孤波子一类研究得出一致性结论的一种对应?
我是针对定位粒子说的,量子力学中的定位粒子的状态是各种自由波的叠加。对于粒子,我们只要关心它的诸多参数和统计特性,这就够了。
作者:bellbasis 时间:2010-07-22 03:09:45
bellbasis你说<"所以这个时候其实和“波“并没什么关系,只是其概率分布长得很像波而已。>
本帖子就是说波的,量子力学也从有波起家的,所以把"波"一脚踢开,总有些不厚道,我认为这可不仅仅是吃水不忘挖井人的一个问题,所以你应该像袁怪侠那样说"并不能因此而认为:物质是主体,波只是它的附属。",呵呵.
=================
是这样的,也许早期理论探索阶段需要借助波动来理解量子力学,但是当体系完善之后并不需要时时考虑这种事情,波动的“效应”包含在解之中。波动形式的引入只是一种中间状态,整个逻辑出发于粒子态,终结于测量的物理量。波动只是中间的数学手段而已。
还有,位置不确定和静止不矛盾。位置不确定说的是你不知道它静止在什么地方,但是它是静止的。对于无数个粒子统计平均后,你会发现这些粒子均匀分布在空间中。这来自量子力学的基本原理。这种效应只有在极其微观才能发现。过度到经典的时候,你不能找到这么一个动量非常精确的平面波,那么你也就可能找到一个位置不那么弥散的准静止粒子,同理,对于delta(x)的情况,经典的情况是你不可能找到一个delta(x)的粒子(位置测量没那么精确)比如可能是一个高斯波包,那么粒子被限定在一个小范围内,同时也允许你测量它的动量,可能也是一个中心在0的高斯波包,那么就是说你能在一定精度内看见一个准静止,准固定位置的粒子,这就是我们的日常生活。
实际上,delta《-》exp(-ipx)是2种极端精确的情况。只有在微观尺度下,才能看见这种极端精确的现象。
本帖子就是说波的,量子力学也从有波起家的,所以把"波"一脚踢开,总有些不厚道,我认为这可不仅仅是吃水不忘挖井人的一个问题,所以你应该像袁怪侠那样说"并不能因此而认为:物质是主体,波只是它的附属。",呵呵.
=================
是这样的,也许早期理论探索阶段需要借助波动来理解量子力学,但是当体系完善之后并不需要时时考虑这种事情,波动的“效应”包含在解之中。波动形式的引入只是一种中间状态,整个逻辑出发于粒子态,终结于测量的物理量。波动只是中间的数学手段而已。
还有,位置不确定和静止不矛盾。位置不确定说的是你不知道它静止在什么地方,但是它是静止的。对于无数个粒子统计平均后,你会发现这些粒子均匀分布在空间中。这来自量子力学的基本原理。这种效应只有在极其微观才能发现。过度到经典的时候,你不能找到这么一个动量非常精确的平面波,那么你也就可能找到一个位置不那么弥散的准静止粒子,同理,对于delta(x)的情况,经典的情况是你不可能找到一个delta(x)的粒子(位置测量没那么精确)比如可能是一个高斯波包,那么粒子被限定在一个小范围内,同时也允许你测量它的动量,可能也是一个中心在0的高斯波包,那么就是说你能在一定精度内看见一个准静止,准固定位置的粒子,这就是我们的日常生活。
实际上,delta《-》exp(-ipx)是2种极端精确的情况。只有在微观尺度下,才能看见这种极端精确的现象。
她为什么不直说?
作者: isisxjy 为什么女生要求一件事的时候总是不直说,而是要拐弯抹角的试探?为什么女生总是缺乏安全感?
男生们很不喜欢这种方式,甚至有的人很鄙视。关于这样的问题,必定是有道理的,但我一直弄不明白,直到今天稍微明白了一点。这归根结底是因为:其一:你以为她是让你完成任务,但事实上她是想证明你在乎她;其二:男生的行为不够可靠。
其实谈恋爱就是个不断测量的过程。从女生的角度讲,男生就是个观测对象;同理从男生的角度讲女生也是个观测对象。按照最简单最传统最普遍的男女关系的情形,女生在选择配偶时十分谨慎,从进化心理学的角度来讲,是因为生育和抚养下一代是个条件苛刻的过程,她们希望可以获得比较好的保障。演化到现在则变为重视感情,在选择配偶时非常谨慎,害怕对方不爱自己。而相应的,男的做事出发点总是在满足女性的具体需求。
而她们的试探就是探测粒子的实验过程。根据大数定律,这样的试验的结果几乎必然的会得到一个确定的靠谱程度。于是女生期望从许多次实验的结果的分布得到全貌,因此会一遍一遍试探,以确保实验的准确性。
为了便于讨论,我们引入靠谱度算符H和试探算符H’。
假设男生对于算符H的本征态是:|真实靠谱率> 和|真实不靠谱率>,一下简写作|a>和|b>。其中a为靠谱的概率,b为不靠谱的概率,a+b=1。
H’即是对男生做各种试探的过程,比如让他给买某个东西、做某些事情。男生对于算符H’的本征态是:|检测靠谱率> 和|检测不靠谱率>,一下简写作|a’>和|b’>。其中a’为表现得靠谱的概率,b’为表现得不靠谱的概率,a’+b’=1。
下面引入一条合理的假定:人人都知道人的表现和心里真实的想法往往并不完全一致,也正因为此,靠谱度算符H和试探算符H’的本征态未必一致。
类似于中微子振荡的味混合矩阵,这两种本征态之间的关系可以用一个关系矩阵表示如下:
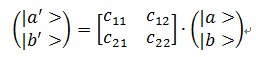
设关系矩阵为A
A中各项的解释如下:
c11:实际靠谱且表现得靠谱的概率;
c12:实际不靠谱但表现得靠谱的概率;
c21:实际靠谱但表现得不靠谱的概率;
c22:实际不靠谱且表现得不靠谱的概率。
由a、b、a'、b'的定义可知这样的定义符合几个概率值的关系。
A的矩阵元还满足以下关系:

但问题是:求A 的逆矩阵时,我们默认了一条假定:detA不为0。
而若假定男生做到女生要求事情和没做到事情的比率并不取决于他是否发自内心的想做,则靠谱和不靠谱表现为靠谱与表现为不靠谱的概率一样(即c11=c12)。此时A 的行列式为0!A矩阵不存在逆矩阵。
从另一个角度而言,奇异矩阵意味着信息的传递不完全。从女生的角度而言,即她无法从|a’>和|b’>唯一确定的对应到|a>和|b>。于是她觉得迷茫,觉得焦虑,她觉得男生做的这些事都不足够证明他心里是真的在乎她,因为他有可能并非发自内心。
出于省事考虑,为了计算更简单,女生们最希望的就是|a’>和|b’>直接等于|a>和|b>,这样她们就不用先根据这个人的种种表现间接猜测A矩阵的矩阵元,然后再求逆矩阵,再做一遍乘法了。这种极端的情况下A矩阵就是单位阵,即实际靠谱则绝对表现靠谱,实际不靠谱则绝对表现不靠谱。c12和c21越接近0,|a’>和|b’>越能直接反映|a>和|b>的值。女生希望的是第一种情况,害怕的是男生的行为与实际想法不相符。
从计算相对麻烦的角度你可以理解女生为什么讨厌所谓的“操作性非常强的追妹子攻略”了吧?(比如那上面建议你在女生跟你说话的时候哪怕你心里烦死了根本没听进去,也要附和她的话,说某一句让人觉得你在关心她的话。)因为这种攻略让男生做违心的事,大大增加了以真实感情为前提的相处的难度(总是要猜测矩阵元,然后算逆矩阵、再做矩阵乘法)。
现在让我们来看下面几个问题:
1、为何女生提要求都不直说?
如果女生对男生的要求全都直说,从交往的过程考虑,一旦直说,男生不论心里是否愿意,通常都不会拒绝。这样的过程正是上面假定的的情况,信息没有得到传播。而如果她不直说,那么只有对她非常关心的男生才可能弄明白她想要什么(注意关心是必要条件,而不是充分条件)。这要求相当苛刻,因为男生可能心里想的是很在乎,但是因为比较笨而导致表现为不靠谱。但它保证了实际情况如果是对方不靠谱的前提下是几乎不可能表现得靠谱的,所以使得detA不可能为0。
2、为何现在的女生越来越容易没有安全感?
现代物质生活越来越发达,许多东西都可以轻易的得到,甚至只要是具体的、实际的东西都可以用钱买到,更甚至大多数需求都不需要太多钱。总而言之,做这些具体的事情相对来讲是很容易的事,一旦满足女生的具体需求这件事对男生而言变得极为容易,就更难判断行列式是否为0了。于是出发点是需要感情的女生们感到很没有安全感。
从这个角度看,之所以有男生口中所谓的“拜金女”,有人结婚要对方买大房子、买很贵的钻戒,这样的人倒是提要求很直接,但是从这个模型的角度讲也未必完全是因为喜欢金钱、喜欢物质生活,而是因为实现这些事情相对比较难,即使提要求很直接,也使得内心并不在乎自己的人几乎不可能愿意花费这样的成本,于是回到之前的讨论结果。
但问题是能买很贵的东西的情况,也只是一两次试验而已,怎么可能在非常多的试验里都让对方买那么贵的东西呢?试验总次数过少,则无法保证试验结果的可靠性,反倒会使得有心无力的人心力交瘁。其实这样的实验本身就不那么可靠。
那么,什么是相对靠谱的实验方式呢?不想强迫对方违心做事而又显得冒冒失失不淑女,且害怕信息流失的女生们其实从小就被社会培养出了一种不直接的说话方式。所以,男生们,不要怪女生拐弯抹角,弄明白她们的道理吧。
——————————————————————————————————————————————————————
那个啥,有人说你为啥不按照量子的规则用几率的语言来表述,用味混合角的sin、cos那几个量来标注矩阵元,而要用概率作为表述方式,你肯定量子力学没我学得好!作者表示:
首先,这是一篇科普文,如果引入几率的语言,我得向一部分人解释一下波函数的几率幅的意义,但这个东西用概率并不影响我们对这个问题的解决和本质性的理解,所以觉得不太有必要;
第二,我希望表述的方法可以和现实结合,如果真实靠谱度的态和检测靠谱度的态之间可以有形式上的与那四个概率直接扯上关系的联系,看起来会更漂亮更亲切;
第三,如果用混合角的sin、cos来作为矩阵元确实是幺正变换,但保证向量的长度不变在这个问题里并不重要,因此我倾向于不要生搬硬套量子的那套规则。你应该完全把这个模型看作另一套规则下的变换;
第四,这是一个想要从基本的定性意义上理解女生行为的很唯象的模型。人心是很复杂的东西,纯粹用量子那套东西来描述其实并不合适。所谓“正确”、“合适”,更多的是在其根本的意义理解上,比如用中微子的质量本征态类比于内心想法,用中微子的味本征态类比于行为;中微子的味混合类比于行为与内心想法之间错综复杂未必一一对应的关系;用探测类比于人们通过观察行为来窥探人心等等。。这个模型最有趣也是令我最开始想到它就兴奋起来的地方正是在此。
欢迎那些批评本文“弱爆了,都没考虑含时过程”“都没考虑振荡”“就学了点线性代数就来BB,不如我们学XX的......”之类的童鞋找到超光速问题的解决方法,然后穿越回过去,在我之前发一篇关于“女生不直说”问题的含时的、考虑振荡的、用某种比物理更牛X的学科的知识等构建的牛X闪闪的《她为什么不直说?》日志,那样我的这篇就不会诞生了。
另外,鉴于一些让人笑破肚子的回复,比如“工科wsn的yy文”“给科大的跪了”“理工男ds要逆袭了!”“作者要是没妹子,肯定是活该的!”作者严正声明:我不是学工科的,我是学物理的。我不是科大的。以及,最重要的:我是女生!我是女生!我是女生!!(人家萌妹子发个照片大家都说:“哇,好可爱 ~”我不就写了个科普文么,怎么就成木有妹子的男ds了
~”我不就写了个科普文么,怎么就成木有妹子的男ds了 。。。“作者要是没妹子,肯定是活该的”,这个倒有点道理!
。。。“作者要是没妹子,肯定是活该的”,这个倒有点道理! )呃又有人说“这样的妹子有男盆友么?”我我我表示我的那位真心不是女的!
)呃又有人说“这样的妹子有男盆友么?”我我我表示我的那位真心不是女的!
最后,本文出发点纯属搞怪,只希求在搞怪中能透出那么点萌萌的感觉、那么点小小的道理,请大家会心一笑,切勿过分较真。
男生们很不喜欢这种方式,甚至有的人很鄙视。关于这样的问题,必定是有道理的,但我一直弄不明白,直到今天稍微明白了一点。这归根结底是因为:其一:你以为她是让你完成任务,但事实上她是想证明你在乎她;其二:男生的行为不够可靠。
其实谈恋爱就是个不断测量的过程。从女生的角度讲,男生就是个观测对象;同理从男生的角度讲女生也是个观测对象。按照最简单最传统最普遍的男女关系的情形,女生在选择配偶时十分谨慎,从进化心理学的角度来讲,是因为生育和抚养下一代是个条件苛刻的过程,她们希望可以获得比较好的保障。演化到现在则变为重视感情,在选择配偶时非常谨慎,害怕对方不爱自己。而相应的,男的做事出发点总是在满足女性的具体需求。
而她们的试探就是探测粒子的实验过程。根据大数定律,这样的试验的结果几乎必然的会得到一个确定的靠谱程度。于是女生期望从许多次实验的结果的分布得到全貌,因此会一遍一遍试探,以确保实验的准确性。
为了便于讨论,我们引入靠谱度算符H和试探算符H’。
假设男生对于算符H的本征态是:|真实靠谱率> 和|真实不靠谱率>,一下简写作|a>和|b>。其中a为靠谱的概率,b为不靠谱的概率,a+b=1。
H’即是对男生做各种试探的过程,比如让他给买某个东西、做某些事情。男生对于算符H’的本征态是:|检测靠谱率> 和|检测不靠谱率>,一下简写作|a’>和|b’>。其中a’为表现得靠谱的概率,b’为表现得不靠谱的概率,a’+b’=1。
下面引入一条合理的假定:人人都知道人的表现和心里真实的想法往往并不完全一致,也正因为此,靠谱度算符H和试探算符H’的本征态未必一致。
类似于中微子振荡的味混合矩阵,这两种本征态之间的关系可以用一个关系矩阵表示如下:
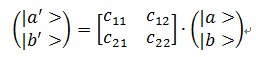
设关系矩阵为A
A中各项的解释如下:
c11:实际靠谱且表现得靠谱的概率;
c12:实际不靠谱但表现得靠谱的概率;
c21:实际靠谱但表现得不靠谱的概率;
c22:实际不靠谱且表现得不靠谱的概率。
由a、b、a'、b'的定义可知这样的定义符合几个概率值的关系。
A的矩阵元还满足以下关系:

但问题是:求A 的逆矩阵时,我们默认了一条假定:detA不为0。
而若假定男生做到女生要求事情和没做到事情的比率并不取决于他是否发自内心的想做,则靠谱和不靠谱表现为靠谱与表现为不靠谱的概率一样(即c11=c12)。此时A 的行列式为0!A矩阵不存在逆矩阵。
从另一个角度而言,奇异矩阵意味着信息的传递不完全。从女生的角度而言,即她无法从|a’>和|b’>唯一确定的对应到|a>和|b>。于是她觉得迷茫,觉得焦虑,她觉得男生做的这些事都不足够证明他心里是真的在乎她,因为他有可能并非发自内心。
出于省事考虑,为了计算更简单,女生们最希望的就是|a’>和|b’>直接等于|a>和|b>,这样她们就不用先根据这个人的种种表现间接猜测A矩阵的矩阵元,然后再求逆矩阵,再做一遍乘法了。这种极端的情况下A矩阵就是单位阵,即实际靠谱则绝对表现靠谱,实际不靠谱则绝对表现不靠谱。c12和c21越接近0,|a’>和|b’>越能直接反映|a>和|b>的值。女生希望的是第一种情况,害怕的是男生的行为与实际想法不相符。
从计算相对麻烦的角度你可以理解女生为什么讨厌所谓的“操作性非常强的追妹子攻略”了吧?(比如那上面建议你在女生跟你说话的时候哪怕你心里烦死了根本没听进去,也要附和她的话,说某一句让人觉得你在关心她的话。)因为这种攻略让男生做违心的事,大大增加了以真实感情为前提的相处的难度(总是要猜测矩阵元,然后算逆矩阵、再做矩阵乘法)。
现在让我们来看下面几个问题:
1、为何女生提要求都不直说?
如果女生对男生的要求全都直说,从交往的过程考虑,一旦直说,男生不论心里是否愿意,通常都不会拒绝。这样的过程正是上面假定的的情况,信息没有得到传播。而如果她不直说,那么只有对她非常关心的男生才可能弄明白她想要什么(注意关心是必要条件,而不是充分条件)。这要求相当苛刻,因为男生可能心里想的是很在乎,但是因为比较笨而导致表现为不靠谱。但它保证了实际情况如果是对方不靠谱的前提下是几乎不可能表现得靠谱的,所以使得detA不可能为0。
2、为何现在的女生越来越容易没有安全感?
现代物质生活越来越发达,许多东西都可以轻易的得到,甚至只要是具体的、实际的东西都可以用钱买到,更甚至大多数需求都不需要太多钱。总而言之,做这些具体的事情相对来讲是很容易的事,一旦满足女生的具体需求这件事对男生而言变得极为容易,就更难判断行列式是否为0了。于是出发点是需要感情的女生们感到很没有安全感。
从这个角度看,之所以有男生口中所谓的“拜金女”,有人结婚要对方买大房子、买很贵的钻戒,这样的人倒是提要求很直接,但是从这个模型的角度讲也未必完全是因为喜欢金钱、喜欢物质生活,而是因为实现这些事情相对比较难,即使提要求很直接,也使得内心并不在乎自己的人几乎不可能愿意花费这样的成本,于是回到之前的讨论结果。
但问题是能买很贵的东西的情况,也只是一两次试验而已,怎么可能在非常多的试验里都让对方买那么贵的东西呢?试验总次数过少,则无法保证试验结果的可靠性,反倒会使得有心无力的人心力交瘁。其实这样的实验本身就不那么可靠。
那么,什么是相对靠谱的实验方式呢?不想强迫对方违心做事而又显得冒冒失失不淑女,且害怕信息流失的女生们其实从小就被社会培养出了一种不直接的说话方式。所以,男生们,不要怪女生拐弯抹角,弄明白她们的道理吧。
——————————————————————————————————————————————————————
那个啥,有人说你为啥不按照量子的规则用几率的语言来表述,用味混合角的sin、cos那几个量来标注矩阵元,而要用概率作为表述方式,你肯定量子力学没我学得好!作者表示:
首先,这是一篇科普文,如果引入几率的语言,我得向一部分人解释一下波函数的几率幅的意义,但这个东西用概率并不影响我们对这个问题的解决和本质性的理解,所以觉得不太有必要;
第二,我希望表述的方法可以和现实结合,如果真实靠谱度的态和检测靠谱度的态之间可以有形式上的与那四个概率直接扯上关系的联系,看起来会更漂亮更亲切;
第三,如果用混合角的sin、cos来作为矩阵元确实是幺正变换,但保证向量的长度不变在这个问题里并不重要,因此我倾向于不要生搬硬套量子的那套规则。你应该完全把这个模型看作另一套规则下的变换;
第四,这是一个想要从基本的定性意义上理解女生行为的很唯象的模型。人心是很复杂的东西,纯粹用量子那套东西来描述其实并不合适。所谓“正确”、“合适”,更多的是在其根本的意义理解上,比如用中微子的质量本征态类比于内心想法,用中微子的味本征态类比于行为;中微子的味混合类比于行为与内心想法之间错综复杂未必一一对应的关系;用探测类比于人们通过观察行为来窥探人心等等。。这个模型最有趣也是令我最开始想到它就兴奋起来的地方正是在此。
欢迎那些批评本文“弱爆了,都没考虑含时过程”“都没考虑振荡”“就学了点线性代数就来BB,不如我们学XX的......”之类的童鞋找到超光速问题的解决方法,然后穿越回过去,在我之前发一篇关于“女生不直说”问题的含时的、考虑振荡的、用某种比物理更牛X的学科的知识等构建的牛X闪闪的《她为什么不直说?》日志,那样我的这篇就不会诞生了。
另外,鉴于一些让人笑破肚子的回复,比如“工科wsn的yy文”“给科大的跪了”“理工男ds要逆袭了!”“作者要是没妹子,肯定是活该的!”作者严正声明:我不是学工科的,我是学物理的。我不是科大的。以及,最重要的:我是女生!我是女生!我是女生!!(人家萌妹子发个照片大家都说:“哇,好可爱
 ~”我不就写了个科普文么,怎么就成木有妹子的男ds了
~”我不就写了个科普文么,怎么就成木有妹子的男ds了最后,本文出发点纯属搞怪,只希求在搞怪中能透出那么点萌萌的感觉、那么点小小的道理,请大家会心一笑,切勿过分较真。
No comments:
Post a Comment