http://www.physixfan.com/archives/2298
nvesting volatility01 boring01 variance01 rentseeking power laws umich : not in case of boring thermodynamic equilibrium, i.e. boring ones, should have correlations which decay exponentially over space and time
伸进去一根探针进等离子体中心,那立刻就会激发起不稳定性于是整个等离子体就会分崩离析
更详细的说明一下这个问题:电动力学告诉我们,在惯性系中,加速运动的带电粒子会向外辐射电磁波,功率与加速度的平方成正比。但是问题是,按照广义相对论的观点,在引力场中静止不动的参考系(下文中称之为S1)并不是一个真正的惯性系,真正的惯性系是自由落体的参考系(下文中称之为S2)。所以说,在真正的惯性系S2中来看,问题中描述的那个带电球其实是在加速运动的,所以说它应该一直有电磁辐射。按照等效原理,在一个S2中有辐射那么在S1中肯定也有辐射。但是问题又来了:如果我们就在S1中看这个问题,那么引力场没有变化、带电球也静止,辐射出去的电磁波的能量是哪来的呢?!
如果有谁想清楚了这个问题或者看到过哪里有比较好的讨论 欢迎email我或者在这里留言!
P.S. 据某大牛说 就算是有辐射 也是非常非常弱的效应 所以说做实验应该是没法观察到的(除非跑到黑洞附近观测)...所以这个问题只能做理论探讨了...
在引力场中静止不动的带电球 会一直辐射电磁波吗?
前几天有个同学跟我讨论了一个很有意思的问题 我到现在也还没有搞明白这个问题的答案到底应该是什么。问题是:在引力场中静止不动的带电球 会一直辐射电磁波吗?更详细的说明一下这个问题:电动力学告诉我们,在惯性系中,加速运动的带电粒子会向外辐射电磁波,功率与加速度的平方成正比。但是问题是,按照广义相对论的观点,在引力场中静止不动的参考系(下文中称之为S1)并不是一个真正的惯性系,真正的惯性系是自由落体的参考系(下文中称之为S2)。所以说,在真正的惯性系S2中来看,问题中描述的那个带电球其实是在加速运动的,所以说它应该一直有电磁辐射。按照等效原理,在一个S2中有辐射那么在S1中肯定也有辐射。但是问题又来了:如果我们就在S1中看这个问题,那么引力场没有变化、带电球也静止,辐射出去的电磁波的能量是哪来的呢?!
如果有谁想清楚了这个问题或者看到过哪里有比较好的讨论 欢迎email我或者在这里留言!
P.S. 据某大牛说 就算是有辐射 也是非常非常弱的效应 所以说做实验应该是没法观察到的(除非跑到黑洞附近观测)...所以这个问题只能做理论探讨了...
人类首次实现能量增益大于1的受控核聚变
受控核聚变的难点在哪里?
作者: physixfan 在知乎上看到这样一个问题:什么是可控核聚变?实现它的难点是什么?。宏观上来看,难点就是同时实现高温高密度和长约束时间(Lawson criterion)。因为自己是聚变方向的PhD,所以我想我可以谈一些比通常见到的科普更多的内容。下文主要针对托卡马克方案(即用磁场约束等离子体以实现聚变的方案),贴自我自己在知乎上对这个问题的回答。
第一方面的难点是物理理论上的。虽然等离子体的运动无非就是麦克斯韦方程组就可以完全描述的,连量子力学都用不到,但是因为包含的粒子数目多,就会遇到本质的困难,此所谓 “More is different”。正如在流体力学里,我们虽然知道基本方程就是Navier-Stokes方程,但是其产生的湍流现象却是物理上几百年来都攻不下来的大山。等离子体同样会产生等离子体湍流,因为有外磁场的存在甚至是比流体湍流更复杂一些。于是在物理上,我们就没有办法找到第一性原理出发找到一个简洁的模型去很好地预测等离子体行为。我们现在所能做的,很多时候就是像流体湍流的研究那样,构建一些更加偏唯像一点的模型,同时发展数值模拟的技术。
第一方面的难点是物理理论上的。虽然等离子体的运动无非就是麦克斯韦方程组就可以完全描述的,连量子力学都用不到,但是因为包含的粒子数目多,就会遇到本质的困难,此所谓 “More is different”。正如在流体力学里,我们虽然知道基本方程就是Navier-Stokes方程,但是其产生的湍流现象却是物理上几百年来都攻不下来的大山。等离子体同样会产生等离子体湍流,因为有外磁场的存在甚至是比流体湍流更复杂一些。于是在物理上,我们就没有办法找到第一性原理出发找到一个简洁的模型去很好地预测等离子体行为。我们现在所能做的,很多时候就是像流体湍流的研究那样,构建一些更加偏唯像一点的模型,同时发展数值模拟的技术。
这种变化可以用雷诺数来量化。雷诺数较小时,黏滞力对流场的影响大于惯性力,流场中流速的扰动会因黏滞力而衰减,流体流动稳定,为层流;反之,若雷诺数较大时,惯性力对流场的影响大于黏滞力,流体流动较不稳定,流速的微小变化容易发展、增强,形成紊乱、不规则的湍流流场。
流态转变时的雷诺数值称为临界雷诺数。临界雷诺数与流场的参考尺寸有密切关系。一般管道流雷诺数Re<2100为层流状态,Re>4000为湍流状态,Re=2100~4000为过渡状态。
在管路设计中,湍流比层流需要更高的泵输出功率。而在热交换器或者反应器设计中,湍流反而有利于热传递或者充分混合.
有效地描述湍流的性质,至今仍然是物理学中的一个重大难题。
作者: physixfan Nature于2014年2月12日发表的一篇文章《Fuel gain exceeding unity in an inertially confined fusion implosion》宣布NIF(美国国家点火装置)用惯性约束聚变的方法首次实现了受控核聚变能量增益大于1的实验,其意为聚变释放出的能量大于输入到靶丸的激光能量,实属受控核聚变道路上的一个重大里程碑!
作为聚变方向的PhD,真心为这个消息感到激动人心,同时想稍微科普一下其中的知识,让行业外的人也了解了解。
受控核聚变能源一直以来就是人类梦寐以求的终极能源。聚变能早在第一颗氢弹爆炸的时候就已经被人类所释放,然而氢弹的本质却决定了它无法作为可控的能源:氢弹爆炸的条件太苛刻,于是只能用原子弹来引爆,而原子弹想要爆炸,浓缩铀的质量就必须大于一个临界值,因此氢弹的爆炸是一定要一次性放出巨大能量的,破坏力实在太大,无法作为能源使用。因此,之后的几十年里,人们就一直在寻求让聚变能每次少量释放的途径。然而,聚变点火的条件是,温度、密度、约束时间这三个量的乘积需要大于一个数值(劳森判据),显而易见的一点是,温度密度越高就约难以约束,因此三者同时提高是一个极其困难的任务。
目前的主流解决方案有两种:磁约束和惯性约束。
磁约束:聚变发生需要的温度太高,大约需要一亿摄氏度,所有实物材料都无法承受如此高温来作为反应容器。但是,带电粒子可以受磁场的作用而改变运动轨迹,因此人们设计了一种用磁场作为反应容器的装置托卡马克,一度是受控核聚变里最接近点火的设计(现在被NIF超越了)。除了托卡马克之外,还有球马克等变种,都属于磁约束。磁约束聚变装置都像是生炉子,只不过炉子的壁是磁场而不是石头罢了。一开始想点燃炉子里的煤是很困难的,需要拿易燃的纸引燃,还要吹风,还不能吹太大的风,但是只要点火成功,之后炉子就可以保证持续燃烧了,只要按时往里添煤就可以了。与此类似,磁约束在理想情况下,也是点火之后就可以持续释放聚变能,然后自己维持温度和约束,持续地释放能量。当然,目前没有成功点火过的装置,但是根据推测,目前正在建造的ITER(完成日期还有好多年TT)是可以达到点火要求的,我们拭目以待。注意能量增益大于1并不意味着可以点火,因为只有一部分能量可以重新加热反应中的等离子体,通常认为需要增益到10左右的时候才能够点火。而如果一但点火成功,等离子体自持燃烧起来了,理想情况下只要不断往里添加燃料和排灰即可,此时的能量增益应为无穷大。
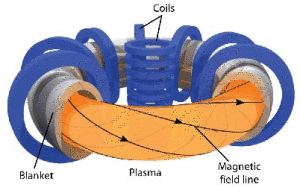
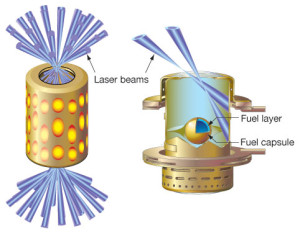
惯性约束:氢弹之所以不能受控地释放能量,原因就在于他得让原子弹引燃。那么,如果不用原子弹,而用其他方式达到高温高密,也许就可以可控的少量释放聚变能了,惯性约束就是这个思路。惯性约束这个名字的意思是,即使氘氚温度极高,也因为自身惯性的原因,并不会在极短的时间内就散开。最近这个突破性实验的发生装置NIF就属于惯性约束。惯性约束聚变就像是爆竹,是一个一个的能量较小的小炸弹,只要每隔一段时间就点燃一个,然后把爆炸的能量想办法收集,就可以是个好的能源。能量增益大于1的意思大概就是,爆竹爆炸释放出的能量终于大于点火用的火柴的输入能量了。但是与爆竹不同的是,点燃惯性约束聚变的靶丸可没那么容易,不仅仅需要功率极高的激光,而且对能量输入的对称性也要求极高。可以想象,如果对称性稍差,那么靶丸就会有的地方凸起有的地方凹陷,最后会变形散开,而不会一致的往里压缩进而形成高密度。对称性的极高要求也就是为什么惯性约束聚变不可以像磁约束那样自持燃烧,聚变释放的能量没有那么高的对称性,不能用来点燃下一个靶丸,必须一个一个的用激光点燃靶丸才行。
群众们对受控核聚变的认识,似乎是好几十年了也做不出什么来。有一种说法是:1950年代,科学家说,50年后人类就可以用上聚变能了;2000年代,科学家说,50年后人类就可以用上聚变能了;现在科学家仍然在说50年后就可以了。。。其实,受控核聚变在过去几十年间的进展也是稳步提高的。实际上几十年前就有磁约束的聚变能释放出来,但是能量输出还小于能量输入。1997年JET装置(托卡马克)上实现了能量增益为0.7;1998年他们宣称能量增益已经达到1.25,但是其实那是拿DD反应间接推算出来的并不是真正的DT聚变。而今NIF装置实现了货真价实的能量增益大于1。目前正在建设当中的ITER目标是能量增益为10。不仅如此,这几十年间人们对聚变等离子体理论的认识也是进展巨大的,越来越小尺度的不稳定性开始被研究和理解,湍流如何被抑制,还有80年代偶然发现的高性能约束H Mode也逐渐被研究利用,等等。
不过,只是能量增益大于1,也还离人们真正能用上聚变能有很长的路要走。这里能量增益的计算方式只是聚变释放能量除以输入到靶丸的激光能量,并没有计算入射出的激光只有一小部分输入到了靶丸里,也没有计算从电能到激光这之间的损耗,更没有考虑从释放出的聚变能(主要由中子携带)转化成最终可以利用的电能这之间又一个巨大的损耗。因此实现真正利用聚变能路途依然遥远啊...不过考虑到NIF半年时间内就把能量增益提高了一个数量级,似乎一切皆有可能呢..!我们既不应过分吹捧这一实验结果,亦不可贬低其重要意义。
希望这一振奋人心的消息能燃起美国政府对聚变的希望,少砍掉一点聚变的经费吧...
作为聚变方向的PhD,真心为这个消息感到激动人心,同时想稍微科普一下其中的知识,让行业外的人也了解了解。
受控核聚变能源一直以来就是人类梦寐以求的终极能源。聚变能早在第一颗氢弹爆炸的时候就已经被人类所释放,然而氢弹的本质却决定了它无法作为可控的能源:氢弹爆炸的条件太苛刻,于是只能用原子弹来引爆,而原子弹想要爆炸,浓缩铀的质量就必须大于一个临界值,因此氢弹的爆炸是一定要一次性放出巨大能量的,破坏力实在太大,无法作为能源使用。因此,之后的几十年里,人们就一直在寻求让聚变能每次少量释放的途径。然而,聚变点火的条件是,温度、密度、约束时间这三个量的乘积需要大于一个数值(劳森判据),显而易见的一点是,温度密度越高就约难以约束,因此三者同时提高是一个极其困难的任务。
目前的主流解决方案有两种:磁约束和惯性约束。
磁约束:聚变发生需要的温度太高,大约需要一亿摄氏度,所有实物材料都无法承受如此高温来作为反应容器。但是,带电粒子可以受磁场的作用而改变运动轨迹,因此人们设计了一种用磁场作为反应容器的装置托卡马克,一度是受控核聚变里最接近点火的设计(现在被NIF超越了)。除了托卡马克之外,还有球马克等变种,都属于磁约束。磁约束聚变装置都像是生炉子,只不过炉子的壁是磁场而不是石头罢了。一开始想点燃炉子里的煤是很困难的,需要拿易燃的纸引燃,还要吹风,还不能吹太大的风,但是只要点火成功,之后炉子就可以保证持续燃烧了,只要按时往里添煤就可以了。与此类似,磁约束在理想情况下,也是点火之后就可以持续释放聚变能,然后自己维持温度和约束,持续地释放能量。当然,目前没有成功点火过的装置,但是根据推测,目前正在建造的ITER(完成日期还有好多年TT)是可以达到点火要求的,我们拭目以待。注意能量增益大于1并不意味着可以点火,因为只有一部分能量可以重新加热反应中的等离子体,通常认为需要增益到10左右的时候才能够点火。而如果一但点火成功,等离子体自持燃烧起来了,理想情况下只要不断往里添加燃料和排灰即可,此时的能量增益应为无穷大。

惯性约束:氢弹之所以不能受控地释放能量,原因就在于他得让原子弹引燃。那么,如果不用原子弹,而用其他方式达到高温高密,也许就可以可控的少量释放聚变能了,惯性约束就是这个思路。惯性约束这个名字的意思是,即使氘氚温度极高,也因为自身惯性的原因,并不会在极短的时间内就散开。最近这个突破性实验的发生装置NIF就属于惯性约束。惯性约束聚变就像是爆竹,是一个一个的能量较小的小炸弹,只要每隔一段时间就点燃一个,然后把爆炸的能量想办法收集,就可以是个好的能源。能量增益大于1的意思大概就是,爆竹爆炸释放出的能量终于大于点火用的火柴的输入能量了。但是与爆竹不同的是,点燃惯性约束聚变的靶丸可没那么容易,不仅仅需要功率极高的激光,而且对能量输入的对称性也要求极高。可以想象,如果对称性稍差,那么靶丸就会有的地方凸起有的地方凹陷,最后会变形散开,而不会一致的往里压缩进而形成高密度。对称性的极高要求也就是为什么惯性约束聚变不可以像磁约束那样自持燃烧,聚变释放的能量没有那么高的对称性,不能用来点燃下一个靶丸,必须一个一个的用激光点燃靶丸才行。

群众们对受控核聚变的认识,似乎是好几十年了也做不出什么来。有一种说法是:1950年代,科学家说,50年后人类就可以用上聚变能了;2000年代,科学家说,50年后人类就可以用上聚变能了;现在科学家仍然在说50年后就可以了。。。其实,受控核聚变在过去几十年间的进展也是稳步提高的。实际上几十年前就有磁约束的聚变能释放出来,但是能量输出还小于能量输入。1997年JET装置(托卡马克)上实现了能量增益为0.7;1998年他们宣称能量增益已经达到1.25,但是其实那是拿DD反应间接推算出来的并不是真正的DT聚变。而今NIF装置实现了货真价实的能量增益大于1。目前正在建设当中的ITER目标是能量增益为10。不仅如此,这几十年间人们对聚变等离子体理论的认识也是进展巨大的,越来越小尺度的不稳定性开始被研究和理解,湍流如何被抑制,还有80年代偶然发现的高性能约束H Mode也逐渐被研究利用,等等。
不过,只是能量增益大于1,也还离人们真正能用上聚变能有很长的路要走。这里能量增益的计算方式只是聚变释放能量除以输入到靶丸的激光能量,并没有计算入射出的激光只有一小部分输入到了靶丸里,也没有计算从电能到激光这之间的损耗,更没有考虑从释放出的聚变能(主要由中子携带)转化成最终可以利用的电能这之间又一个巨大的损耗。因此实现真正利用聚变能路途依然遥远啊...不过考虑到NIF半年时间内就把能量增益提高了一个数量级,似乎一切皆有可能呢..!我们既不应过分吹捧这一实验结果,亦不可贬低其重要意义。
希望这一振奋人心的消息能燃起美国政府对聚变的希望,少砍掉一点聚变的经费吧...
受控核聚变的难点在哪里?
作者: physixfan 在知乎上看到这样一个问题:什么是可控核聚变?实现它的难点是什么?。宏观上来看,难点就是同时实现高温高密度和长约束时间(Lawson criterion)。因为自己是聚变方向的PhD,所以我想我可以谈一些比通常见到的科普更多的内容。下文主要针对托卡马克方案(即用磁场约束等离子体以实现聚变的方案),贴自我自己在知乎上对这个问题的回答。
第一方面的难点是物理理论上的。虽然等离子体的运动无非就是麦克斯韦方程组就可以完全描述的,连量子力学都用不到,但是因为包含的粒子数目多,就会遇到本质的困难,此所谓 “More is different”。正如在流体力学里,我们虽然知道基本方程就是Navier-Stokes方程,但是其产生的湍流现象却是物理上几百年来都攻不下来的大山。等离子体同样会产生等离子体湍流,因为有外磁场的存在甚至是比流体湍流更复杂一些。于是在物理上,我们就没有办法找到第一性原理出发找到一个简洁的模型去很好地预测等离子体行为。我们现在所能做的,很多时候就是像流体湍流的研究那样,构建一些更加偏唯像一点的模型,同时发展数值模拟的技术。
第二方面的难点是物理实验上的。即使没有第一性原理出发的理论,很多时候唯像模型也可以非常实用,比如说现在流体湍流的模型就可以在工程上很实用。但是等离子体实验的数据可并不像流体那么好获得。从理论上我们可以知道,托卡马克里的高温高密度等离子体会有非常多的不稳定性,如果伸进去一根探针进等离子体中心,那立刻就会激发起不稳定性于是整个等离子体就会分崩离析。基于这个原因,实验观测的手段就会很受限制。这也就是为什么我们不说“等离子体测量”一词,而是使用“等离子体诊断”,因为这的确就跟诊断病人的病情很像。
基于以上两点物理上的原因,可以说我们没能很好地理解托卡马克里等离子体的运动,因此对装置的设计就没有那么给力,只能慢慢发展慢慢改进...实际的历史进程就是,实验上发现一种不稳定性,然后理论在之后的几年里争取理解它,然后想办法改进设计去抑制这个不稳定性。但是抑制了之后,约束改进了,又会在实验上发现更小时空尺度上的不稳定性,于是再理论去理解,再改进设计,循环往复...我们的确是在不断进步的,只是需要时间。
第三方面的难点是工程上的。从理论上我们现在知道,如果想要达到聚变的点火条件,那么在工程上我们需要在足够大的体积内产生足够强的磁场(约为10T)。而现在人类能实现的最大稳定磁场大概也就是10T那样一个量级了(我一直在想如果人类能做到比现在大十倍的磁场的话,可能我们早就用上聚变能了...)。产生这么大的磁场的电磁铁,一定是需要巨大的电流的,而巨大的电流就会发热,发热了之后就会把材料自己烧掉...所以现在正在建的最大的托卡马克工程ITER就是采用的超导线圈的方式,这的确是解决了发热问题,但是线圈想要维持超导,就需要极低温,通液氦浸泡。所以你可以想想这样一副场景么:在一个房间里,内部温度是一亿摄氏度的超高温,墙壁温度是几开尔文的超低温...工程上的实现难度可想而知。
最后一方面的难点...是经济上的...做那么大的超导电磁铁,得花多少钱哪。。。于是现在最大的托卡马克工程ITER就根本不是一个国家在做了,而是7个国家一起出钱合作的,目前老是超预算(一超就是上billion美元的),于是不断延期。。。美国这边,因为投钱去了ITER,不光已经没有预算在本土建新的托卡马克了,就连老的也开始关门大吉了一些...我们这苦命的专业啊...
不过我对聚变的看法还是积极的。虽然现在美国没钱了,但是似乎中国还是既有钱又有激情来做聚变的。小道消息称中国在近期将要自己做一个本来计划在ITER之后建的DEMO装置,中国人民勤劳能干,很有可能比ITER先完成。按照经验规律,如果按照他们说的指标建起来的话,实现点火应该是没问题的。我们就这样一点一点制造更大的装置,发现新的问题,理解新的物理现象,再改进装置的设计,聚变能的到来并不是天方夜谭!
Jul 4, 2011 - I used to work in plasma physics. A plasma is just a gas -- say, simple hydrogen gas -- which has been heated up to the point where the atoms ...
How swarming theory could inform plasma physics and financial markets ... be used to analyse plasma in the solar wind and movements in financial markets.
University of Warwick How swarming theory could inform plasma physics and financial markets (более 101 песен) скачать или слушать онлайн бесплатно.
Aug 24, 2007 - Warwick Podcast – How swarming theory could inform plasma physics and financial markets. Writing about web page ...
... for physicists interested in the statistical properties of financial markets. ... Applied & Technical Physics; Atomic, Molecular, Optical & Plasma Physics ...
Aug 23, 2007 - ... Wicks talks about how a tool to analyse swarming could be used to analyse plasma in the solar wind and movements in financial markets.
nvesting volatility01 boring01 variance01 rentseeking power laws umich : not in case of boring thermodynamic equilibrium, i.e. boring ones, should have correlations which decay exponentially over space and time
http://vserver1.cscs.lsa.umich.edu/~crshalizi/notabene/power-laws.html
http://quantivity.wordpress.com/2012/01/03/physics-biology-peltzman-finance/#more-9021
variance hits like blk swan in groups
Notebooks
Why do physicists care about power laws so much? I'm probably not the best person to speak on behalf of our tribal obsessions (there was a long debate among the faculty at my thesis defense as to whether "this stuff is really physics"), but I'll do my best. There are two parts to this: power-law decay of correlations, and power-law size distributions. The link is tenuous, at best, but they tend to get run together in our heads, so I'll treat them both here. The reason we care about power law correlations is that we're conditioned to think they're a sign of something interesting and complicated happening. The first step is to convince ourselves that in boring situations, we don't see power laws. This is fairly easy: there are pretty good and rather generic arguments which say that systems in thermodynamic equilibrium, i.e. boring ones, should have correlations which decay exponentially over space and time; the reciprocals of the decay rates are the correlation length and the correlation time, and say how big a typical fluctuation should be. This is roughly first-semester graduate statistical mechanics. (You can find those arguments in, say, volume one of Landau and Lifshitz's Statistical Physics.) Second semester graduate stat. mech. is where those arguments break down --- either for systems which are far from equilibrium (e.g., turbulent flows), or in equilibrium but very close to a critical point (e.g., the transition from a solid to liquid phase, or from a non-magnetic phase to a magnetized one). Phase transitions have fluctuations which decay like power laws, and many non-equilibrium systems do too. (Again, for phase transitions, Landau and Lifshitz has a good discussion.) If you're a statistical physicist, phase transitions and non-equilibrium processes define the terms "complex" and "interesting" --- especially phase transitions, since we've spent the last forty years or so developing a very successful theory of critical phenomena. Accordingly, whenever we see power law correlations, we assume there must be something complex and interesting going on to produce them. (If this sounds like the fallacy of affirming the consequent, that's because it is.) By a kind of transitivity, this makes power laws interesting in themselves. Since, as physicists, we're generally more comfortable working in the frequency domain than the time domain, we often transform the autocorrelation function into the Fourier spectrum. A power-law decay for the correlations as a function of time translates into a power-law decay of the spectrum as a function of frequency, so this is also called "1/f noise". Similarly for power-law distributions. A simple use of the Einstein fluctuation formula says that thermodynamic variables will have Gaussian distributions with the equilibrium value as their mean. (The usual version of this argument is not very precise.) We're also used to seeing exponential distributions, as the probabilities of microscopic states. Other distributions weird us out. Power-law distributions weird us out even more, because they seem to say there's no typical scale or size for the variable, whereas the exponential and the Gaussian cases both have natural scale parameters. There is a connection here with fractals, which also lack typical scales, but I don't feel up to going into that, and certainly a lot of the power laws physicists get excited about have no obvious connection to any kind of (approximate) fractal geometry. And there are lots of power law distributions in all kinds of data, especially social data --- that's why they're also called Pareto distributions, after the sociologist. Physicists have devoted quite a bit of time over the last two decades to seizing on what look like power-laws in various non-physical sets of data, and trying to explain them in terms we're familiar with, especially phase transitions. (Thus "self-organized criticality".) So badly are we infatuated that there is now a huge, rapidly growing literature devoted to "Tsallis statistics" or "non-extensive thermodynamics", which is a recipe for modifying normal statistical mechanics so that it produces power law distributions; and this, so far as I can see, is its only good feature. (I will not attempt, here, to support that sweeping negative verdict on the work of many people who have more credentials and experience than I do.) This has not been one of our more successful undertakings, though the basic motivation --- "let's see what we can do!" --- is one I'm certainly in sympathy with. There have been two problems with the efforts to explain all power laws using the things statistical physicists know. One is that (to mangle Kipling) there turn out to be nine and sixty ways of constructing power laws, and every single one of them is right, in that it does indeed produce a power law. Power laws turn out to result from a kind of central limit theorem for multiplicative growth processes, an observation which apparently dates back to Herbert Simon, and which has been rediscovered by a number of physicists (for instance, Sornette). Reed and Hughes have established an even more deflating explanation (see below). Now, just because these simple mechanisms exist, doesn't mean they explain any particular case, but it does mean that you can't legitimately argue "My favorite mechanism produces a power law; there is a power law here; it is very unlikely there would be a power law if my mechanism were not at work; therefore, it is reasonable to believe my mechanism is at work here." (Deborah Mayo would say that finding a power law does not constitute a severe test of your hypothesis.) You need to do "differential diagnosis", by identifying other, non-power-law consequences of your mechanism, which other possible explanations don't share. This, we hardly ever do. Similarly for 1/f noise. Many different kinds of stochastic process, with no connection to critical phenomena, have power-law correlations. Econometricians and time-series analysts have studied them for quite a while, under the general heading of "long-memory" processes. You can get them from things as simple as a superposition of Gaussian autoregressive processes. (We have begun to awaken to this fact, under the heading of "fractional Brownian motion".) The other problem with our efforts has been that a lot of the power-laws we've been trying to explain are not, in fact, power-laws. I should perhaps explain that statistical physicists are called that, not because we know a lot of statistics, but because we study the large-scaled, aggregated effects of the interactions of large numbers of particles, including, specifically, the effects which show up as fluctuations and noise. In doing this we learn, basically, nothing about drawing inferences from empirical data, beyond what we may remember about curve fitting and propagation of errors from our undergraduate lab courses. Some of us, naturally, do know a lot of statistics, and even teach it --- I might mention Josef Honerkamp's superb Stochastic Dynamical Systems. (Of course, that book is out of print and hardly ever cited...) If I had, oh, let's say fifty dollars for every time I've seen a slide (or a preprint) where one of us physicists makes a log-log plot of their data, and then reports as the exponent of a new power law the slope they got from doing a least-squares linear fit, I'd at least not grumble. If my colleagues had gone to statistics textbooks and looked up how to estimate the parameters of a Pareto distribution, I'd be a happier man. If any of them had actually tested the hypothesis that they had a power law against alternatives like stretched exponentials, or especially log-normals, I'd think the millennium was at hand. (If you want to know how to do these things, please read this paper, whose merits are entirely due to my co-authors.) The situation for 1/f noise is not so dire, but there have been and still are plenty of abuses, starting with the fact that simply taking the fast Fourier transform of the autocovariance function does not give you a reliable estimate of the power spectrum, particularly in the tails. (On that point, see, for instance, Honerkamp.)
See also: Chaos and Dynamical Systems; Complex Networks; Self-Organized Criticality; Time Series; Tsallis Statistics
第一方面的难点是物理理论上的。虽然等离子体的运动无非就是麦克斯韦方程组就可以完全描述的,连量子力学都用不到,但是因为包含的粒子数目多,就会遇到本质的困难,此所谓 “More is different”。正如在流体力学里,我们虽然知道基本方程就是Navier-Stokes方程,但是其产生的湍流现象却是物理上几百年来都攻不下来的大山。等离子体同样会产生等离子体湍流,因为有外磁场的存在甚至是比流体湍流更复杂一些。于是在物理上,我们就没有办法找到第一性原理出发找到一个简洁的模型去很好地预测等离子体行为。我们现在所能做的,很多时候就是像流体湍流的研究那样,构建一些更加偏唯像一点的模型,同时发展数值模拟的技术。
第二方面的难点是物理实验上的。即使没有第一性原理出发的理论,很多时候唯像模型也可以非常实用,比如说现在流体湍流的模型就可以在工程上很实用。但是等离子体实验的数据可并不像流体那么好获得。从理论上我们可以知道,托卡马克里的高温高密度等离子体会有非常多的不稳定性,如果伸进去一根探针进等离子体中心,那立刻就会激发起不稳定性于是整个等离子体就会分崩离析。基于这个原因,实验观测的手段就会很受限制。这也就是为什么我们不说“等离子体测量”一词,而是使用“等离子体诊断”,因为这的确就跟诊断病人的病情很像。
基于以上两点物理上的原因,可以说我们没能很好地理解托卡马克里等离子体的运动,因此对装置的设计就没有那么给力,只能慢慢发展慢慢改进...实际的历史进程就是,实验上发现一种不稳定性,然后理论在之后的几年里争取理解它,然后想办法改进设计去抑制这个不稳定性。但是抑制了之后,约束改进了,又会在实验上发现更小时空尺度上的不稳定性,于是再理论去理解,再改进设计,循环往复...我们的确是在不断进步的,只是需要时间。
第三方面的难点是工程上的。从理论上我们现在知道,如果想要达到聚变的点火条件,那么在工程上我们需要在足够大的体积内产生足够强的磁场(约为10T)。而现在人类能实现的最大稳定磁场大概也就是10T那样一个量级了(我一直在想如果人类能做到比现在大十倍的磁场的话,可能我们早就用上聚变能了...)。产生这么大的磁场的电磁铁,一定是需要巨大的电流的,而巨大的电流就会发热,发热了之后就会把材料自己烧掉...所以现在正在建的最大的托卡马克工程ITER就是采用的超导线圈的方式,这的确是解决了发热问题,但是线圈想要维持超导,就需要极低温,通液氦浸泡。所以你可以想想这样一副场景么:在一个房间里,内部温度是一亿摄氏度的超高温,墙壁温度是几开尔文的超低温...工程上的实现难度可想而知。
最后一方面的难点...是经济上的...做那么大的超导电磁铁,得花多少钱哪。。。于是现在最大的托卡马克工程ITER就根本不是一个国家在做了,而是7个国家一起出钱合作的,目前老是超预算(一超就是上billion美元的),于是不断延期。。。美国这边,因为投钱去了ITER,不光已经没有预算在本土建新的托卡马克了,就连老的也开始关门大吉了一些...我们这苦命的专业啊...
不过我对聚变的看法还是积极的。虽然现在美国没钱了,但是似乎中国还是既有钱又有激情来做聚变的。小道消息称中国在近期将要自己做一个本来计划在ITER之后建的DEMO装置,中国人民勤劳能干,很有可能比ITER先完成。按照经验规律,如果按照他们说的指标建起来的话,实现点火应该是没问题的。我们就这样一点一点制造更大的装置,发现新的问题,理解新的物理现象,再改进装置的设计,聚变能的到来并不是天方夜谭!
The Physics of Finance: Natural chaos in the markets
physicsoffinance.blogspot.com/2011/07/natural-chaos-in-markets.html
You visited this page on 8/24/14.
How swarming theory could inform plasma physics and ...
www.podcastpedia.org/.../How-swarming-theory-could-inform-plasma-p...
University of Warwick How swarming theory could inform ...
poiskm.com/.../27006426-University-of-Warwick-Ho...
Translate this page
Translate this page
How swarming theory could inform plasma physics and ...
https://blogs.warwick.ac.uk/medialog/entry/how_swarming_theory/
The Statistical Mechanics of Financial Markets - Springer
How Swarming Theory Could Inform Plasma Physics And ...
https://player.fm/1DrmJ
nvesting volatility01 boring01 variance01 rentseeking power laws umich : not in case of boring thermodynamic equilibrium, i.e. boring ones, should have correlations which decay exponentially over space and time
http://vserver1.cscs.lsa.umich.edu/~crshalizi/notabene/power-laws.html
http://quantivity.wordpress.com/2012/01/03/physics-biology-peltzman-finance/#more-9021
variance hits like blk swan in groups
Notebooks
Power Law Distributions, 1/f Noise, Long-Memory Time Series
05 Sep 2013 11:26Why do physicists care about power laws so much? I'm probably not the best person to speak on behalf of our tribal obsessions (there was a long debate among the faculty at my thesis defense as to whether "this stuff is really physics"), but I'll do my best. There are two parts to this: power-law decay of correlations, and power-law size distributions. The link is tenuous, at best, but they tend to get run together in our heads, so I'll treat them both here. The reason we care about power law correlations is that we're conditioned to think they're a sign of something interesting and complicated happening. The first step is to convince ourselves that in boring situations, we don't see power laws. This is fairly easy: there are pretty good and rather generic arguments which say that systems in thermodynamic equilibrium, i.e. boring ones, should have correlations which decay exponentially over space and time; the reciprocals of the decay rates are the correlation length and the correlation time, and say how big a typical fluctuation should be. This is roughly first-semester graduate statistical mechanics. (You can find those arguments in, say, volume one of Landau and Lifshitz's Statistical Physics.) Second semester graduate stat. mech. is where those arguments break down --- either for systems which are far from equilibrium (e.g., turbulent flows), or in equilibrium but very close to a critical point (e.g., the transition from a solid to liquid phase, or from a non-magnetic phase to a magnetized one). Phase transitions have fluctuations which decay like power laws, and many non-equilibrium systems do too. (Again, for phase transitions, Landau and Lifshitz has a good discussion.) If you're a statistical physicist, phase transitions and non-equilibrium processes define the terms "complex" and "interesting" --- especially phase transitions, since we've spent the last forty years or so developing a very successful theory of critical phenomena. Accordingly, whenever we see power law correlations, we assume there must be something complex and interesting going on to produce them. (If this sounds like the fallacy of affirming the consequent, that's because it is.) By a kind of transitivity, this makes power laws interesting in themselves. Since, as physicists, we're generally more comfortable working in the frequency domain than the time domain, we often transform the autocorrelation function into the Fourier spectrum. A power-law decay for the correlations as a function of time translates into a power-law decay of the spectrum as a function of frequency, so this is also called "1/f noise". Similarly for power-law distributions. A simple use of the Einstein fluctuation formula says that thermodynamic variables will have Gaussian distributions with the equilibrium value as their mean. (The usual version of this argument is not very precise.) We're also used to seeing exponential distributions, as the probabilities of microscopic states. Other distributions weird us out. Power-law distributions weird us out even more, because they seem to say there's no typical scale or size for the variable, whereas the exponential and the Gaussian cases both have natural scale parameters. There is a connection here with fractals, which also lack typical scales, but I don't feel up to going into that, and certainly a lot of the power laws physicists get excited about have no obvious connection to any kind of (approximate) fractal geometry. And there are lots of power law distributions in all kinds of data, especially social data --- that's why they're also called Pareto distributions, after the sociologist. Physicists have devoted quite a bit of time over the last two decades to seizing on what look like power-laws in various non-physical sets of data, and trying to explain them in terms we're familiar with, especially phase transitions. (Thus "self-organized criticality".) So badly are we infatuated that there is now a huge, rapidly growing literature devoted to "Tsallis statistics" or "non-extensive thermodynamics", which is a recipe for modifying normal statistical mechanics so that it produces power law distributions; and this, so far as I can see, is its only good feature. (I will not attempt, here, to support that sweeping negative verdict on the work of many people who have more credentials and experience than I do.) This has not been one of our more successful undertakings, though the basic motivation --- "let's see what we can do!" --- is one I'm certainly in sympathy with. There have been two problems with the efforts to explain all power laws using the things statistical physicists know. One is that (to mangle Kipling) there turn out to be nine and sixty ways of constructing power laws, and every single one of them is right, in that it does indeed produce a power law. Power laws turn out to result from a kind of central limit theorem for multiplicative growth processes, an observation which apparently dates back to Herbert Simon, and which has been rediscovered by a number of physicists (for instance, Sornette). Reed and Hughes have established an even more deflating explanation (see below). Now, just because these simple mechanisms exist, doesn't mean they explain any particular case, but it does mean that you can't legitimately argue "My favorite mechanism produces a power law; there is a power law here; it is very unlikely there would be a power law if my mechanism were not at work; therefore, it is reasonable to believe my mechanism is at work here." (Deborah Mayo would say that finding a power law does not constitute a severe test of your hypothesis.) You need to do "differential diagnosis", by identifying other, non-power-law consequences of your mechanism, which other possible explanations don't share. This, we hardly ever do. Similarly for 1/f noise. Many different kinds of stochastic process, with no connection to critical phenomena, have power-law correlations. Econometricians and time-series analysts have studied them for quite a while, under the general heading of "long-memory" processes. You can get them from things as simple as a superposition of Gaussian autoregressive processes. (We have begun to awaken to this fact, under the heading of "fractional Brownian motion".) The other problem with our efforts has been that a lot of the power-laws we've been trying to explain are not, in fact, power-laws. I should perhaps explain that statistical physicists are called that, not because we know a lot of statistics, but because we study the large-scaled, aggregated effects of the interactions of large numbers of particles, including, specifically, the effects which show up as fluctuations and noise. In doing this we learn, basically, nothing about drawing inferences from empirical data, beyond what we may remember about curve fitting and propagation of errors from our undergraduate lab courses. Some of us, naturally, do know a lot of statistics, and even teach it --- I might mention Josef Honerkamp's superb Stochastic Dynamical Systems. (Of course, that book is out of print and hardly ever cited...) If I had, oh, let's say fifty dollars for every time I've seen a slide (or a preprint) where one of us physicists makes a log-log plot of their data, and then reports as the exponent of a new power law the slope they got from doing a least-squares linear fit, I'd at least not grumble. If my colleagues had gone to statistics textbooks and looked up how to estimate the parameters of a Pareto distribution, I'd be a happier man. If any of them had actually tested the hypothesis that they had a power law against alternatives like stretched exponentials, or especially log-normals, I'd think the millennium was at hand. (If you want to know how to do these things, please read this paper, whose merits are entirely due to my co-authors.) The situation for 1/f noise is not so dire, but there have been and still are plenty of abuses, starting with the fact that simply taking the fast Fourier transform of the autocovariance function does not give you a reliable estimate of the power spectrum, particularly in the tails. (On that point, see, for instance, Honerkamp.)
See also: Chaos and Dynamical Systems; Complex Networks; Self-Organized Criticality; Time Series; Tsallis Statistics
No comments:
Post a Comment