white Hausdorff空间就是连续点空间 开集 任意并 开集、闭集, 开集：所有点都是内点, 闭集：聚点都在集合内 ; 开集三性质：1.空集和全集是开集 2.任意并, 3.有限交

http://noteonx.blogspot.com/search/label/math

基础数学（泛函）

1. Convex Optimization 附录 A 是个很简洁易懂的参考。
2. Machine learning and pattern recognition 的附录
3. latex project / MyMathNote
4. 小本笔记本

泛函

空间是点的集合。
1.1  距离空间
距离满足：

1. 非负性
2. 对称性
3. 三角不等式

定义了距离的空间为距离空间或度量空间。

若集合 X 中的每个基本列都收敛，则称 X 为完备的距离空间。
1.1.1 开集、闭集
这些都是距离空间中就可以定义的。
内点：存在邻域在集合内
开集：所有点都是内点。
聚点：x_0 的所有邻域都包含集合中不同于 x_0 的点
导集：全体聚点的集合
闭包：集合及其导集的并
闭集：聚点都在集合内

开集三性质：

1. 空集和全集是开集
2. 任意并
3. 有限交

1.2 {线性空间}

规定了线性运算的空间为线性空间或向量空间。线性运算的系数域为实数或者复数域。

1.3{线性赋范空间，巴拿赫空间}

范数的性质：

1. 非负
2. 标量积,||ax|| = |a|*||x||
3. 三角不等式

定义了范数的线性空间称为线性赋范空间。由范数可诱导距离，因此线性赋范空间是距离空间，

完备的线性赋范空间称为巴拿赫空间。


1.4 {内积空间，希尔伯特空间}

内积的性质

1. 对称共轭
2. 首项线性
3. 非负

内积有一个重要性质，Cauchy-Schwarz 不等式。

定义了内积的线性空间称为内积空间。

有限维实内积空间称为欧式空间。有限维复内积空间称为酉空间。

完备的内积空间称为希尔伯特空间。

内积可以诱导范数，内积空间为线性赋范空间，由柯西不等式可推导三角不等式。

内积空间的标准正交系。格兰-施密特方法。

完全的标准正交系：不存在非零元素，使它和所有 $e^n$ 正交。

1.4.1 {等距变换}
等距变换是在内积空间中定义的，并且是线性变换。
等距变换等价于保持向量的长度。特别的，对于欧式空间，还等价于保持内积。（对于内积空间，保持内积必定保持距离）

酉空间中等距变换对应酉矩阵。欧式空间中，等距变换对应正交矩阵。




R^n 上的 Lp norm (p >= 1)

L1 范数
L2
L\infty 最大绝对值

R^n 上的所有范数都是凸的。

问题：L0 范数 - 非零元素个数
1. L0 不是一个真正的范数，范数定义中 scaling 的性质就不满足。

2. L0 范数不是凸的。

x = (0,0) y=(1,1)
l0(x)=0, l0(y)=2, 0.5 l0(x)+0.5 l0(y)=1
l0(0.5 x+0.5 y)=2

凸函数的两个判定
1. 一阶
2. 二阶 hessian 矩阵为半正定，这是充分必要条件，hessian 对应该点处的曲率

定义：
The inequality is tight 指 >= 在某些情况下，会出现等式 =
同样的表述还有 tight bound


哪些常见的函数是凸的？




学习微分几何——Hausdorff空间就是连续点空间

已有 2336 次阅读 2011-12-31 15:04 |个人分类:电脑围棋|系统分类:科研笔记|关键词:空间，流形

强调流形是Hausdorff空间是为了说明流形的无限可分性。

一个很强的说法就是：Hausdorff空间是任意两点的开集都可以不相交的空间。开集不相交，就说明无论两点之间如何靠近，它们之间总不会有公共的相邻点。

 

再复习流形的定义：实（复）n维流形是这样一个Haustorff空间，它的每点处有开邻域，与实（复）n维线性空间的开集同胚。

再次理解：

开集和开邻域无非是说一个空间的点与周围的点的关系，也就是对空间的微分元素之间的关系。流形的定义，其实就是把实线性空间的定义进行拓展的空间。所进行的拓展，就是剥离对点之间的距离的关注，只保留点之间的顺序的关注，看实线性空间所能变成的样子是什么——这些能变成的空间，就叫流形。——也就是与实线性空间具有同胚的微分结构的空间，就是流形。

 

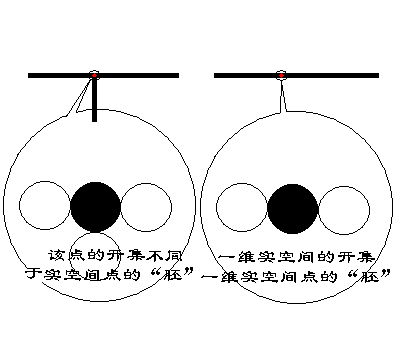
为什么说“圆”是一维的流形呢？

 

这个“T”就不是流形：

本文引用地址：http://blog.sciencenet.cn/blog-33982-524068.html  此文来自科学网邱嘉文博客，转载请注明出处。