phymath999: 廣義相對論預言下的引力波是以波形式傳播的時空擾動，被形象地稱為“空漪”（Ripples in Spacetime）[11]。廣義相對論下的弱引力場可寫作對平直時空的線性微擾

Friday, March 27, 2015

廣義相對論預言下的引力波是以波形式傳播的時空擾動，被形象地稱為“空漪”（Ripples in Spacetime）[11]。廣義相對論下的弱引力場可寫作對平直時空的線性微擾

creaders.net swd 终极思维／上帝信仰是关键

引力的本質是什麼

送交者: swd 2010月03月03日13:06:28 于 [教育學術] 發送悄悄話

回答:質量和引力的兩個問題,看如何回答? 由 swd 于2010-03-02 20:21:26

gravity wave是留給地球科學與流體力學中另一種性質迥異的波動。關于引力的本質是什麼，愛因斯坦則認為是一種跟電磁波一樣的波動，稱為引力波。引力波是時空曲率的擾動以行進波的形式向外傳遞。引力輻射是另外一種稱呼，指的是這些波從星體或星系中輻射出來的現象。電荷被加速時會發出電磁輻射，同樣有質量的物體被加速時就會發出引力輻射，這是廣義相對論的一項重要預言。

引力波的存在而且也真的無所不在，是廣義相對論中一項毫不模糊的預言。所有目前相互競爭而且被“認可”的重力理論（認可︰與現前可得一切證據能達到相當準確度的相符）所預言的引力輻射特質即各有千秋；而原則上，這些預言有時候和廣義相對論所預言的相差甚遠。但很不幸地，現在要確認引力輻射的存在性就已相當具有挑戰性，更不用說要研究它的細節。
引力波的基礎理論

線性愛因斯坦方程

引力波——時空的波紋（示意圖）

廣義相對論預言下的引力波是以波形式傳播的時空擾動，被形象地稱為“空漪”（Ripples in Spacetime）^[11]。廣義相對論下的弱引力場可寫作對平直時空的線性微擾︰（以下采用自然單位，引力常數G = 光速c = 1）

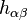$g_{alpha eta} = eta_{alpha eta} + h_{alpha eta},$ ，其中 $|h_{alpha eta}|<<1,$
這里 $eta_{alpha eta} = diag(-1, 1, 1, 1),$ 是平直時空的閔可夫斯基度規， $h_{alpha eta},$ 是弱引力場帶來的微擾。在這個度規下計算得到的黎曼張量為

$R_{alpha eta mu u} = frac{1}{2}left( partial_mu partial_ eta h_{alpha u} - partial_mu partial_alpha h_{ eta u} + partial_ u partial_alpha h_{ eta mu} - partial_ u partial_ eta h_{alpha mu} ight)$
愛因斯坦張量為

$G_{alpha eta} = -frac{1}{2} left( partial_mu partial^mu overline{h}_{alpha eta} + eta_{alpha eta} partial^mu partial^ u overline{h}_{mu u} - partial_ eta partial^mu overline{h}_{alpha mu} - partial_alpha partial^mu overline{h}_{ eta mu} ight)$
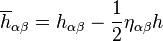這里 $overline{h}_{alpha eta} = h_{alpha eta} - frac{1}{2}eta_{alpha eta}h$ ， $h = eta^{alpha eta} h_{alpha eta},$ ， $overline{h}_{alpha eta},$ 被稱作跡反轉度規微擾（trace-reverse metric perturbation）。
如果采用洛倫茨規範，愛因斯坦張量的後三項將為零，這里洛倫茨規範的形式為

$partial^ eta overline{h}_{alpha eta} = 0$
事實上總可以選擇這樣的規範條件，並且洛倫茨規範不是唯一的，意味著坐標在一個無窮小的線性坐標變換下仍滿足洛倫茨規範，關于這一點請參考有關規範變換的內容。
在洛倫茨規範下，愛因斯坦張量為

$G_{alpha eta} = -frac{1}{2}partial_mu partial^mu overline{h}_{alpha eta} = -frac{1}{2} Box^2 overline{h}_{alpha eta}$
代入愛因斯坦引力場方程 $G_{alpha eta} = 8pi T_{alpha eta},$ ，

$Box^2 overline{h}_{alpha eta} = -16pi T_{alpha eta},$
這個方程又叫弱引力場中的線性愛因斯坦方程。在遠源（ $T_{alpha eta} = 0,$ ）的情形下，得到帶有達朗貝爾算符的四維波方程︰

$Box^2 overline{h}_{alpha eta} = 0,$

引力波的傳播
上面波方程的一般解為如下本征函數的線性疊加︰

$overline{h}_{alpha eta} = A_{alpha eta}exp{left(i mathbf{k cdot x} ight)}$
其中 $A_{alpha eta},$ 是四維振幅， $mathbf{k},$ 是四維波矢，滿足條件

$eta_{alpha eta} k^{alpha} k^{ eta} = 0 ,$ ，這表明引力波傳播經過的測地線是零性的，即其傳播速度是光速。
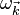四維波矢 $k^{alpha} = left(omega_{vec k}, vec k ight),$ ，其中 $omega_{vec k},$ 是波的角頻率， $vec k$ 是經典的三維波矢。由于洛倫茨規範並不唯一，此時坐標還不是完全確定的。如果再加上條件︰

$overline{h}_{t i} = 0 ,$

$eta_{alpha eta}overline{h}^{alpha eta} = 0 ,$

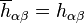第一個條件表示引力波張量中所有與時間t有關的分量都為零，第二個條件表示引力波張量矩陣的跡為零。因此這組規範條件叫做轉置無跡規範（transverse traceless gauge），簡稱TT規範。在TT規範下， $overline{h}_{alpha eta} = h_{alpha eta} ,$ 。由洛倫茨規範和TT規範共同決定下的引力波張量只有兩個分量是獨立的，它們實際對應著引力波的兩種偏振態。對于在z方向傳播的波矢 $k^{alpha} = left(omega, 0, 0, omega ight),$ ，這兩個振動分量垂直于傳播方向，這表明引力波和電磁波一樣是橫波，其張量形式寫作

引力波的 $h_{+},$ 偏振對質點位置的調制

引力波的 $h_{$ 偏振對質點位置的調制

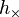$h_{alpha eta} = egin{pmatrix} 0 & 0 & 0 & 0\ 0 & h_{+} & h_{ imes} & 0\ 0 & h_{ imes} & -h_{+} & 0\ 0 & 0 & 0 & 0 end{pmatrix}$
$h_{+},$ 和 $h_{ imes},$ 是引力波的兩種偏振態，右圖中示意了兩種偏振各自不同的振動形式。

引力波的輻射
有源的線性愛因斯坦方程解釋了波源的運動如何產生引力輻射︰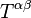

$Box^2 overline{h}^{alpha eta} = -16pi T^{alpha eta},$
類似用泊松方程求解牛頓引力勢，運用格林函數可得到帶有推遲勢的一般解︰

$overline{h}^{alpha eta} left( t, vec x ight) = 4 int operatorname{d}^3 x^prime frac{T^{alpha eta} left( t - |vec x - vec x^prime|, vec x^prime ight)}{|vec x - vec x^prime|}$
這里 $T^{alpha eta},$ 所處在的時間是 $t - |vec x - vec x^prime|,$ ，表示引力波從源點 $vec x^prime,$ 傳播到場點 $vec x,$ 經過了時間為 $|vec x - vec x^prime|,$ 的延遲。
在遠場近似和長波極限下，格林函數解近似為

$overline{h}^{alpha eta} left( t, vec x ight) approx frac{4}{r} int operatorname{d}^3 x^prime T^{alpha eta}left( t - r, vec x^prime ight)$
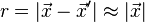其中標量 $r = |vec x - vec x^prime| approx |vec x|,$ 是源點到場點的距離。
相對論中波源的質能守恆和動量守恆合起來寫作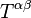

$T^{alpha eta}_{, eta} = 0 ,$
因此動量-能量張量 $T^{alpha eta},$ 中的 $T^{tt},$ （質量-能量密度）和其他所有和時間t有關的分量 $T^{i t},$ （動量密度）對時間的偏導數都為零，代入後方程的解可進一步化簡為

$overline{h}^{alpha eta} = frac{2}{r}frac{operatorname{d}^2 Q^{alpha eta}left( t -r ight)} {operatorname{d} t^2}$
這即是引力輻射的四極矩近似公式，描述了一個弱相對論系統引力輻射的最基本情形。其中 $Q^{alpha eta},$ 描述了波源的質量-能量分布

$Q^{alpha eta} = int ho x^{primealpha} x^{prime eta}, operatorname{d}^3 x^prime$
這里張量 $Q^{alpha eta},$ 即是系統的質量四極矩（轉動慣量張量），而 $ho equiv T^{tt},$ 是波源的質量-能量密度，積分範圍是整個波源內部。
四極矩公式的物理意義是引力輻射起始于隨時間二階變化（例如諧振）的四極矩，這一點與電磁輻射不同︰電磁輻射起始于隨時間二階變化的偶極矩。這一區別的來源是︰一個隨時間二階變化的電偶極矩或磁偶極矩對應著電荷密度中心的振動，這一振動是隨意不受限制的；而一個隨時間二階變化的質量的偶極矩對應著質心的振動，這一振動不能滿足動量守恆定律，因此不存在這樣對時間二階偏導不為零的質量偶極矩。由于四極矩是偶極矩的更高階項，這也是引力輻射要遠弱于電磁輻射的原因

相对论量子化学新进展-金属材料文库系统 - 热门文辑

wenku.satipm.com/view_81wx408gx7rzs2gz.html
轉為繁體網頁

所谓的相对论效应并不是一个可观测的物理量，而是指有限光速与无限光速之间的所有差别。 !"#$ 年， %&'()* ,-.( 提出了奠定（非相对论）量子力学基础的%&'()* ,-.

音乐快递：的相对论效应并不是一个可观测的物理量，而是指 ...

bbs.wenxuecity.com › 论坛 › 音乐快递
轉為繁體網頁

的相对论效应并不是一个可观测的物理量，而是指有限光速与无限光速之间的所有差别. 来源: marketreflections 于2011-10-31 20:16:57 [档案] [博客] [旧帖] [给我 ...

音乐快递：所谓的相对论效应并不是一个可观测的物理量，而是 ...

bbs.wenxuecity.com › 论坛 › 音乐快递 - 轉為繁體網頁

2011年4月25日 - 文件格式: PDF/Adobe Acrobat - 快速查看 ... 有效质量变为零(即无. 质量粒子). 这种无质量粒子的运动由狄拉克方程. 而非传统的薛定谔方程描述.

phymath999: 在低温状况，电磁振子的平均能量与能量均分 ...

phymath999.blogspot.com/2012/08/blog-post_7275.html
轉為繁體網頁

2012年8月15日 - 的相对论效应并不是一个可观测的物理量，而是指有限光速与无限光速之间的所有差别 -marketreflections- ♂ 给marketreflections 发送悄悄话 ...

薛定谔方程其实是Dirac方程在光速无限大时的近似

phymath999.blogspot.com/2012/08/dirac_15.html
轉為繁體網頁

2012年8月15日 - 的相对论效应并不是一个可观测的物理量，而是指有限光速与无限光速之间的所有差别 -marketreflections- ♂ 给marketreflections 发送悄悄话 ...

相对论量子化学新进展_百度文库

220.181.112.102/.../d4e2187ab307e87100f69606.html?re...
轉為繁體網頁

2014年3月4日 - 所谓的相对论效应并不是一个可观测的物理量，而是指有限光速与无限光速之间的所有差别。 !"#$ 年， %&'()*+,-.( 提出了奠定（非相对论）量子力学 ...

相对论量子化学新进展- 豆丁网

www.docin.com/p-973175555.html - 轉為繁體網頁

2014年11月28日 - 所谓的相对论效应并不是一个可观测的物理量,而是指有限光速与无限光速之间的所有差别HJ.1926 年,Schrfdinger 提出了奠定(非相对论)量子力学 ...

相对论量子化学新进展_刘文剑- 豆丁网

www.docin.com › 幼儿/小学教育 › 教育管理
轉為繁體網頁

2014年9月30日 - 所谓的相对论效应并不是一个可观测的物理量, 而是指有限光速与无限光速之间的所有差别[ 1] 。1926 年, SchrÊdinger 提出了奠定( 非相对论) 量子 ...

為了提供最相關的搜尋結果，我們省略了部分與目前顯示結果非常類似的項目 (8 個)。
如有需要，您可以重新執行搜尋並顯示所有結果。

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)