phymath999: 两个下标是对称的.士兵在指南車的指引下矢量沿曲线的平移

Sunday, March 29, 2015

http://hillyuan.blogspot.com/2013/08/blog-post.html
.

上善若水

2013年8月23日星期五

矢量沿曲线的平移

话说黄帝蚩尤大战于涿鹿, 其时浓雾弥漫, 不知东西. 黄帝造指南車辨识道路......

Fig.1 Parralel transport of a vector along a great circle of the sphere

现在考虑A部落的士兵在指南車的指引下向正南C, D部落的士兵在指南車的指引下也向正南C前进, 当他们在C点汇合时发现A,D指南車的指向是不同的!这一结果与我们在欧式空间的平行的概念大不相同.

曲面上的"平行移动"・协变导数

上面的例子说明我们需要重新定义所谓平行这一概念. 不与欧式空间的平行的概念相冲突, 我们小心地定义所谓平行是矢量V沿曲线U的方向导数为零
$\nabla_{U}V=0$
注意到上述导数其实尚未有明确的定义,我们把球面上的矢量V写成球坐标形式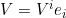 $V=V^ie_i$
,其在欧式空间中沿 $\nu$ 轴的方向导数为
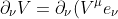$\partial_\nu V=\partial_\nu(V^\mu e_\nu)=(\partial_\nu V^\mu)e_\mu+V^\mu\partial_\nu e_\mu$
将基矢的偏导表述为基矢和球面法向n的线性函数
$e_{\mu,\nu}={\Gamma ^{\lambda}}_{\mu\nu}e_\lambda+K_{\mu\nu}n$
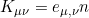该式称为高斯方程. 这里 ${\Gamma ^{\lambda}}_{\mu\nu}$ 为克氏符, $K_{\mu\nu}=e_{\mu,\nu}n$ 为Weingarten方程. 注意到 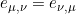$e_{\mu,\nu}=e_{\nu,\mu}$ , K和

Γ 的两个下标是对称的.

但对于黄帝部落而言,他们只知道球面上的东西,对球面外的法线一无所知! 在球面世界上来看, 上述方向导数为
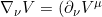$\nabla_\nu V=(\partial_\nu V^\mu)e_\mu+V^\lambda {\Gamma ^{\mu}}_{\lambda\nu}e_\mu=(\partial_\nu V^\mu+V^\lambda {\Gamma ^{\mu}}_{\lambda\nu})e_\mu$
在这里 $\nabla_\nu V$ 称为矢量V沿

ν 轴的协变或绝对导数, 与欧式空间中方向导数相比较, 它去掉了球面法向的变化, 如下图

Fig.2 欧式空间的平行移动(V->V')和曲面空间的平行移动(V->V'')([1]p.102)

   矢量沿曲线的协变导数为零就是矢量沿曲线的平行移动条件.

   现在把矢量V沿方向U的协变导数写成 $\mathbf{T}(\mathbf{V},\mathbf{U})=\nabla_\mathbf{U}\mathbf{V}$ .可以看出 $\nabla\mathbf{V}=T(\cdot ,\mathbf{U})$ 是一(1,1)张量, 称为协变导数. $\nabla_\mathbf{U}\mathbf{V}=\mathbf{U}\nabla\mathbf{V}$

   2. 克氏符・联络
   在欧式空间中克氏符的计算方法在高斯方程中给出.在曲面(黎曼)空间中,我们先要定义其度规, 然后设度规沿任一曲线的协变导数为零,由此推出克氏符的计算方法,称为与度规相适配的克氏符.
$\nabla_ag_{ab}=\partial _ag_{ab}-{\Gamma ^{d}}_{ab}g_{dc}-{\Gamma ^{d}}_{ac}g_{db}=\partial _ag_{ab}-\Gamma _{cab}-\Gamma _{bac}=0$
交换上式下标abc的顺序可的
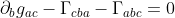
$\partial _bg_{ac}-\Gamma _{cba}-\Gamma _{abc}=0$
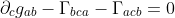
$\partial _cg_{ab}-\Gamma _{bca}-\Gamma _{acb}=0$
由此可以得到
${\Gamma ^{c}}_{ab}=\frac{1}{2}g^{cd}\left ( \partial _ag_{bd}+ \partial _bg_{ad}- \partial _dg_{ab}\right )$
称为Levi-Civita联络. 克氏联络还有一个简单的表达式([3]p106-108)
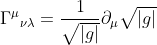
${\Gamma ^{\mu}}_{\nu\lambda}=\frac{1}{\sqrt{\left | g \right |}}\partial _{\mu}\sqrt{\left | g \right |}$
由此
$\nabla_\mu V^\nu=\frac{1}{\sqrt{\left | g \right |}}\partial _\mu\left ( \sqrt{\left | g \right |} V^\mu\right )$

   3. 1形式的协变导数
   考虑一标量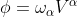 $\phi =\omega _\alpha V^\alpha$
$\phi_{,\beta}=\omega _\alpha {V^{\alpha}}_{,\beta}+\omega _{\alpha,\beta}V^\alpha =\omega _\alpha \left (V{^{\alpha}}_{\beta}+\Gamma {^{\alpha}}_{\gamma\beta }\right )+\left (\omega_{\alpha,\beta}-{\Gamma ^{\gamma}}_{\alpha\beta}\omega_\gamma \right )V^\alpha =\omega_\alpha \nabla_{\beta}V^\alpha+\left (\omega_{\alpha,\beta}-{\Gamma ^{\gamma}}_{\alpha\beta}\omega_\gamma \right )V^\alpha$
可定义
$\nabla_\beta\omega _\alpha=\omega_{\alpha,\beta}-{\Gamma ^{\gamma}}_{\alpha\beta}\omega_\gamma \right$
为1形式的协变导数.由于上面方程的左边和倒数第二项都是张量, 该1形式的协变导数也是张量. 此时
$\nabla_\beta \phi =\omega _\alpha\nabla_\beta V^\alpha +\nabla_\beta\omega _\alpha V^\alpha$

主要参考文献
1. A. Zee, Einstein Gravity in a Nutshell, 2013, Princeton University
2. B.F.Schutz, Geometrical methods of mathematical physics, 1980, Cambridge Univeristy
3. S. Weinberg, Gravitation and cosmology: Principles and applications of the general theory of relativity, 1971, John Wiley & Sons

phymath999

Sunday, March 29, 2015

两个下标是对称的.士兵在指南車的指引下矢量沿曲线的平移

2013年8月23日星期五

矢量沿曲线的平移

No comments:

Post a Comment

Sunday, March 29, 2015

两个下标是对称的.士兵在指南車的指引下 矢量沿曲线的平移

2013年8月23日星期五

矢量沿曲线的平移

No comments:

Post a Comment

两个下标是对称的.士兵在指南車的指引下矢量沿曲线的平移