https://zx31415.wordpress.com/tag/mathematical-physics/page/3/
记录运动皮层100个神经元信号，解码生成肌肉和手部运动
n 从而大脑信号绕过脊髓，直接触发FES设备，实现了有意
图的、大脑控制的肌肉收缩，重建手部运动
能量-动量张量
在Newton的万有引力理论中，质量是引力之源。狭义相对论进一步教给我们：(1)质量和能量是同一的：
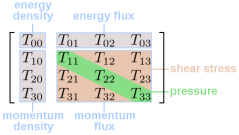
；(2) Lorentz不变性要求我们将能量和动量联系起来。上述观点的产物是称为能量-动量张量的2阶对称协变张量
。
(能量-动量守恒) 
。
。
注意，与普通导数相比，协变导数要多出一项，这正是引力场带走的能量-动量
，因而对于缓慢运动的粒子，时间项是绝对主项，且所有空间坐标对时间的导数均可忽略。在这一极限下，测地线方程约化为
，故
是引力场的主项；
，故
是引力势的主项。这就是时空结构决定引力场的方式。另一方面，万有引力定律的Gauss形式给出
。情况已较为明朗：同为联络场的导数，将确定曲率。若这一关系是线性的，则所得的曲率张量应是2阶对称的：首选自然是Ricci曲率
No comments:
Post a Comment