图中心纠缠光源发出的孪生光子A和B分别传送给Alice和Bob。 Alice 处有半透半反分光器BS等，对A以及准备隐形传态的光子X，作刚才我们所描述的“同时符合”贝尔测量，将测量的结果：“符合”或“不符合”，通过经典通道，比如微波天线，发射给远在另一端（多瑙河对岸）的Bob。然后，Bob便需要对他所拥有的B，或者说是，从多瑙河底的光纤信道（量子通道）传过来的光子，作一些我们上一节中提到过的“变换处理”。
比较起Alice的“贝尔测量”来说，Bob的“变换处理”操作要简单多了，因为实际上，在Alice用X和A完成贝尔测量的那一霎那，X、A、B三粒子之间，已经完成了“纠缠转移”：原来不纠缠的X和A纠缠起来，光子X原来量子态的大部分信息，已经转移到B。比如在Alice作的“同时符合”贝尔测量情况下，Bob只需要根据从微波天线接受到的信息，对光纤信道传来的光子，作点小变换：如果微波信息是“符合”，什么也不作；如果微波信息是不“符合”，则将传来的光子的偏振方向变成与原方向垂直。上面所说的目的，用得到的微波信息，连到一个电光转换开关，再控制偏振器，即可达到。像在上图中，Bob的圆圈中所显示的那样。
到此为止，原来的光子X的所有信息都转移到了Bob所拥有的光子B上。而实际上，Alice和Bob从始至终都对X上的这些信息一无所知，他们唯一所知道的只是： 最后，X和A成为纠缠单态，Bob的粒子有了原来X的所有性质，隐形传态完成了。
在量子隐形传态的实验中，调节每个光子之间的时间差，做到两个光子必须“同时”到达测量仪器，对隐形传态的成功与否至关重要。
“贝尔测量”也是影响传态保真度的重要因素。因为利用线性光学元件，不能完全区分四个贝尔态。因此，要实现完全的贝尔测量，就需要采取另外一些办法。一个方法是使用非线性的光学器件（见参考资料）。
另外一条路就是采取“连续变量”纠缠源来实现量子隐形传态。
我们在此文中所叙述的量子纠缠及其在量子信息中的应用，基本是基于以单光子偏振态为代表的 “分离变量”方法。实际上，也有不少实验室研究所谓“连续变量”的量子信息技术。连续变量量子信息，是以光场正交振幅和正交位相分量为代表。“分离变量”对应于有限维的状态空间，可以用简单的量子力学算符和方程准确描述，而“连续变量”对应于无限维的状态空间，解释起来不容易。两种方式各有优点与不足，比如对量子隐形传态来说，用连续变量方法，可以做到完全的贝尔测量，理想情况下的贝尔探测效率可达100%。在此我们不多谈两种方式的优缺点，目前也有人提出hybrid 的方案，即是将分离变量和连续变量量子资源结合起来，发展混合型的量子信息技术。
可喜的是，对量子信息的研究和实验方面，中国的学者们，走在了国际科研的前沿。除了使用分离变量方法的中科大-清华团队之外，山西大学光电研究所在连续变量量子信息方面做了很多突出的工作，他们的实验室，不仅在国内连续变量领域是独此一家，在世界上也可算是这方面几个有代表性的实验室之一。他们在2004年，最早实现了连续变量的量子隐形传输。2006年，他们的研究团队利用连续变量量子纠缠，设计和实现了量子保密通信，并证明了它在长距离传输中的安全性（见参考资料）。
量子隱形傳輸
文/李建二
摘 要
近十年來「量子資訊(quantum information)」開始萌芽發展，本文針對其中重要之一環「量子隱形傳輸」(quantum teleportation) 作入門之介紹。
|
一、引言
很多人看過「星際航行(star trek)」這部電視連續劇。我第一次觀賞這個節目是在三十年前正在美國求學的時候，看到「航海家(Voyager)」星艦上的艦長柯克(Kirk)站在「傳輸室(transporter)」內，室外一位艦員按下控制鍵，柯克便罩在耀眼的光芒下，很快變淡，成稀疏光點而消逝，隨即在星艦下星球之某處(預先選定)，先出現光點，再模糊形象，然後柯克出現了，這情境相信在很多人心理留下深刻的印象和懂憬，整個過程包含實体分解、實体傳輸及實体組合等三個步驟，人類的科學是否真的能夠建構這樣的設備？也許， 在遙遠(？)的未來，近十年來「量子資訊(quantum information)」開始萌芽發展，物理學家已經可以初步做到把一個光子的狀態傳輸到另一個不相干的光子上，這就是本文要介紹的「量子隱形傳輸」[1]。
二、什麼是量子隱形傳輸 ？
量子隱形傳輸是量子計算和量子資訊中重要的一環，它們都嘗試應用量子系統來從事計算、儲存及傳輸資訊，任一量子系統所處的狀態稱之為量子態，在不同的環境和刺激下，可以處於不同的量子態，量子隱形傳輸廣義來說如下：把系統A之任一量子態經過一套設備完整地傳輸到系統B。這不是拷貝，因為原來系統A之量子態在傳輸後完全被破壞了。但這樣的定義也包含了這種情形：系統A和系統B間可以相互作用，如果排除這種可能，就得到一般所認知的量子隱形傳輸：系統A和系統B 可以相距遙遠(譬如在銀河之兩端)，彼此間無任何作用之可能。在這樣的情況下，把系統A之任一量子態經過一套設備(包括古典通訊)完整地傳輸到系統B。要大約了解這是如何做到，也就是它的機制，則先要介紹一些量子系統完全異於古典系統的特殊性質。
三、量子態
前面提到的量子系統，它的演變是依據量子理論來進行，其量子態也完全由量子理論來決定。 實際上所有在巨觀世界及微觀世界的系統都是量子理論適用的範疇，只是在巨觀世界裡量子的行為一般都不顯著，在這樣的情形下，量子理論趨近於古典理論而運用到巨觀現象。而在微觀世界理，古典理論不能適用，微觀現象只能用量子理論來描述。所以這裡所提的量子系統都是微觀世界裡的系統，如分子、原子、電子、光子、量子點(quantum dot)、輻射場等。以下將以光子為例說明量子態及其特殊性。
從量子理論的觀點，電磁波是由一群光子所組成。每一光子具有動量及兩個極化態(polarization)。這三者互相垂直，我們把這兩個極化態叫做水平極化態和垂直極化態，分別以
及 
表示之並以之作為基本態，任意之極化態則是基本態之任意線性疊合如下：
及 表示之並以之作為基本態，任意之極化態則是基本態之任意線性疊合如下：
(1)
其中 
和 
是任意複數，
代表在狀態
之機率，且其總機率為壹： 
。 亦即當你對此光子做測量時得到水平極化態之機率是
，而得到垂直極化態之機率是
。但在量子理論中，測量(measurement)有其特殊性：如果你量到的是水平極化態，則測量後，此光子就保持在此水平極化態，亦即原本之狀態
在測量時被破壞而崩潰(Collapse)成測量後之水平極化態。所以一次的測量，是無法決定，而且又把破壞了，這就是說如果你想把一個你不知道的光子狀態傳輸給別人，你想靠測量此光子以獲得及，進而告知對方進而重組是不可能的。
和 是任意複數，代表在狀態之機率，且其總機率為壹： 。 亦即當你對此光子做測量時得到水平極化態之機率是，而得到垂直極化態之機率是。但在量子理論中，測量(measurement)有其特殊性：如果你量到的是水平極化態，則測量後，此光子就保持在此水平極化態，亦即原本之狀態在測量時被破壞而崩潰(Collapse)成測量後之水平極化態。所以一次的測量，是無法決定，而且又把破壞了，這就是說如果你想把一個你不知道的光子狀態傳輸給別人，你想靠測量此光子以獲得及，進而告知對方進而重組是不可能的。
四、糾纏態
上一節介紹了一個光子的量子態。本節將介紹由兩個光子組成的系統之量子態。我們一樣只考慮光子的極化態，並選擇
為基底(即基態之集合)。其中底標1(2)代表第一(二)個光子， 兩-光子之極化態可以分為兩類，第一類是兩個光子的極化態各自獨立互不關連，其一般式可寫成 
， 其中
為基底(即基態之集合)。其中底標1(2)代表第一(二)個光子， 兩-光子之極化態可以分為兩類，第一類是兩個光子的極化態各自獨立互不關連，其一般式可寫成 ， 其中 
(2)
且 
上面的基態都屬於此類。 第二類是兩個光子的極化態不能寫成各自狀態之張量乘積(tensor product)，亦即 
。 我們稱之為兩-光子之糾纏態(entangled state)。在糾纏態中，兩個光子之極化態互相關連，不受時空之限制，亦即具有非侷域性關連(non-local correlation)。我們也可以選擇四個正規(orthonormal) 糾纏態作為基底，常用的稱之為貝爾態(Bell states)，其形式如下：
, 
(3)
上面的基態都屬於此類。 第二類是兩個光子的極化態不能寫成各自狀態之張量乘積(tensor product)，亦即 。 我們稱之為兩-光子之糾纏態(entangled state)。在糾纏態中，兩個光子之極化態互相關連，不受時空之限制，亦即具有非侷域性關連(non-local correlation)。我們也可以選擇四個正規(orthonormal) 糾纏態作為基底，常用的稱之為貝爾態(Bell states)，其形式如下： , (3)
我們以
糾纏態為例來進一步說明，在此態中它告訴我們第一個光子在水平極化態而第二個光子在垂直極化態之機率是1/2，同樣的第一個光子在垂直極化態而第二個光子在水平極化態之機率也是1/2，因此各別光子之極化態是任意(Random)而未知的，但如果我們對第一個光子進行測量而得到水平極化態，則第二個光子就自動地瞬間地處在垂直極化態，不管它離第一個光子有多遠(譬如在銀河的另一端)，這就是所謂的非侷域性關連， 這種現象是完全非古典的，貝爾狀態又稱為 EPR 偶(EPR Pairs)，其中E代表愛因斯坦，PR是另外兩位物理學家(B. Podolsky and N. Rosen)，他們三人於1935 [2]年發表一篇著名的論文質疑非侷域性關連及量子力學之完整性，引起相當熱烈的論辨，後來實驗肯定了非侷域性關連的存在。
糾纏態為例來進一步說明，在此態中它告訴我們第一個光子在水平極化態而第二個光子在垂直極化態之機率是1/2，同樣的第一個光子在垂直極化態而第二個光子在水平極化態之機率也是1/2，因此各別光子之極化態是任意(Random)而未知的，但如果我們對第一個光子進行測量而得到水平極化態，則第二個光子就自動地瞬間地處在垂直極化態，不管它離第一個光子有多遠(譬如在銀河的另一端)，這就是所謂的非侷域性關連， 這種現象是完全非古典的，貝爾狀態又稱為 EPR 偶(EPR Pairs)，其中E代表愛因斯坦，PR是另外兩位物理學家(B. Podolsky and N. Rosen)，他們三人於1935 [2]年發表一篇著名的論文質疑非侷域性關連及量子力學之完整性，引起相當熱烈的論辨，後來實驗肯定了非侷域性關連的存在。 |
五、貝爾態測量
一個光子的水平或垂直極化態可以用檢極器(Analyzer)或極化分光器(polarized beam splitter)來分析， 如果測量的結果是水平極化， 則測量後此光子原先之狀態即崩潰而變成水平態，對兩個光子之系統，我們也可以去量各別光子的水平或垂直極化態，如果測量的結果是第一個光子是水平態，第二個光子是垂直態，則測量後此系統之原先狀態便崩潰成
態，但我們不一定要量光子的水平或垂直極化態，也可以直接設法去測量兩光子之貝爾態，則測量後此兩光子系統便處在所量到的貝爾態上，這就是所謂的貝爾態測量(Bell state measurement)。兩光子貝爾態測量中，主要的設備是 50：50 分光器(beam splitter)。當兩光子同時抵達分光器時，兩光子之波包( wave packet)相互重疊，因而產生干涉( interference)效應，每一個光子經過分光器後可能繼續前進或被反射，調整分光器使兩光子離開分光器後之兩個途徑之對應狀態相互疊合，以用一個分光器作貝爾態測量為例如圖一，
我們在光子離開分光器(BS)出來的兩個途徑上各置一個光子偵測器(detector) d1及d2，並僅對兩個偵測器同時偵測到光子時作記錄，這就是所謂的同時量測(coincidence measurement)。這樣的設置意謂每一出來的途徑必須有一個光子，所以只有兩個可能：兩個光子經過分光器時都繼續前進或同時被反射，因為這兩種情形是無法區分的，所以出來後之兩光子態是這兩種情形之狀態之線性疊合(linear superposition)，其振幅(amplitude)大小相同而異號，因為兩光子之任意狀態都可以上述之四個正交(orthogonal)的貝爾態之線性疊合來表示，但觀察這些貝爾態在把兩個光子對調下，只有變號，其它保持不變，所以在這樣的實驗設置下，只有貝爾態是容許的，其他都相互抵消了，也就是量到了一個貝爾態，而原來兩光子之狀態也崩潰成此貝爾態了。
即崩潰而變成水平態，對兩個光子之系統，我們也可以去量各別光子的水平或垂直極化態，如果測量的結果是第一個光子是水平態，第二個光子是垂直態，則測量後此系統之原先狀態便崩潰成態，但我們不一定要量光子的水平或垂直極化態，也可以直接設法去測量兩光子之貝爾態，則測量後此兩光子系統便處在所量到的貝爾態上，這就是所謂的貝爾態測量(Bell state measurement)。兩光子貝爾態測量中，主要的設備是 50：50 分光器(beam splitter)。當兩光子同時抵達分光器時，兩光子之波包( wave packet)相互重疊，因而產生干涉( interference)效應，每一個光子經過分光器後可能繼續前進或被反射，調整分光器使兩光子離開分光器後之兩個途徑之對應狀態相互疊合，以用一個分光器作貝爾態測量為例如圖一， 我們在光子離開分光器(BS)出來的兩個途徑上各置一個光子偵測器(detector) d1及d2，並僅對兩個偵測器同時偵測到光子時作記錄，這就是所謂的同時量測(coincidence measurement)。這樣的設置意謂每一出來的途徑必須有一個光子，所以只有兩個可能：兩個光子經過分光器時都繼續前進或同時被反射，因為這兩種情形是無法區分的，所以出來後之兩光子態是這兩種情形之狀態之線性疊合(linear superposition)，其振幅(amplitude)大小相同而異號，因為兩光子之任意狀態都可以上述之四個正交(orthogonal)的貝爾態之線性疊合來表示，但觀察這些貝爾態在把兩個光子對調下，只有
變號，其它保持不變，所以在這樣的實驗設置下，只有貝爾態是容許的，其他都相互抵消了，也就是量到了一個貝爾態，而原來兩光子之狀態也崩潰成此貝爾態了。
六、量子隱形傳輸之機制
於1993年由IBM 特別研究員(IBM Fellow) Charles H. Bennett [3] 領導的國際研究團隊共六人，聯名發表一篇文章，證明在原先系統上之狀態被破壞下，完全的量子隱形傳輸在理論上是實際可能的。在此之前，科學家們並不認為它真的可行，因為它破壞了量子力學中的測不準原理(uncertainty principle)。這個原理說明不可能經由一次測量而得知系統之所有資訊，譬如對一個粒子的位子量的愈正確，則它的動量就愈不正確， 且對該粒子之干擾也愈嚴重，終於完全破壞了該粒子之原先狀態且無法得知所有資訊，因此無法據以再造一個具有完全相同狀態的粒子，所以認為完全的量子隱形傳輸是不可能的，但是Bennett 的研究團隊應用量子力學中所特有的糾纏態，不必要去量知原先粒子之所有資訊而在理論上達成完全的量子隱形傳輸，底下我們描述這個機制。
 |
假定甲、乙、丙三個人各自擁有一個粒子，分別稱為1、2、3粒子，甲扮演委託人的角色，在粒子1上製造了一個狀態
後，交給乙。乙扮演寄件者之角色，將把狀態傳輸給丙所擁有的粒子3。在這裡丙扮演接收者的角色，乙跟丙所擁有的粒子2及粒子3事先就製成為糾纏態後，再各自擁有，乙收到甲送來的粒子1後，便對粒子1及粒子2作貝爾態測量，量到某個貝爾態後，便以古典通訊方式，如電話，通知丙其測量的結果，丙依據測量的結果對粒子3作適當處理使粒子3處在粒子1原先要傳輸的狀態上，因此達成了完全的量子隱形傳輸，在這整個傳輸過程中，乙跟丙都不知道是甚麼狀態，而且粒子1上之原先狀態完全被破壞了，所以這不是拷貝，而是真正的傳輸，粒子2及粒子3間之糾纏態是重要的關鍵，因為在乙對粒子1及粒子2作了貝爾態測量後，粒子2之狀態變了，丙所擁有的粒子3之狀態自動且瞬間地跟著改變了，不管乙和丙相距多遠，所以丙只要依據乙貝爾態測量之結果，作相對應唯一的處理就可以使粒子3 處在狀態上，因為需要古典通訊以告知測量結果，所以這個傳輸不是瞬間的，而仍然受限於相對論，即訊息的傳送不能比光速快，之所以稱為「隱形」是因為在傳輸過程中，除了開始和最後，都沒有出現，這個機制不僅適用於純態，也適用於非純態。
七、量子隱形傳輸之實驗
Bennett 研究團隊所提出的機制一直到1997年才在澳大利亞Innsbruck 大學由Anton Zeilinger [4] 所領導的研究團隊第一次作出來。 Innsbruck 實驗成功地把一個光子的任意極化態完整地傳輸到另一個光子上， 但是成功的機率只有25%，這是因為在作貝爾態測量時，他們用的方法就是上面所介紹的貝爾態測量，這個方法只能量到一個貝爾態，其他三個貝爾態則量不到，因為四個貝爾態出現的機率是相同的，所以成功地傳輸的機率只有25%，Innsbruck 實驗之基本架構如圖二。其後在1998年初，在義大利羅馬大學的研究團隊[5]應用兩個糾纏的光子，並把每個光子之兩個自由度，動量和極化態，一齊考慮進來，他們在一個光子上應用這兩個自由度建構了不同的貝爾態，而要傳輸的極化態是在其中一個光子上調出來的，他們成功地把極化態由一個光子傳輸到另一個光子上，這兩光子的傳輸裝置只能傳輸純態，非純態就無能為力了，同年年底，在美國加州理工學院由Jeff Kimble[6]領導的光學研究團隊發表了一個完全成功的量子隱形傳輸，只是他們用的不是三個或兩個光子而是幅射場(Radiation Field)，所用的狀態不是極化態或動量而是一致態(coherent state)，在他們的裝置下，可以測量所有的貝爾態，因此甲送進之狀態皆能傳輸到丙，傳輸機率為100%。
，其他三個貝爾態則量不到，因為四個貝爾態出現的機率是相同的，所以成功地傳輸的機率只有25%，Innsbruck 實驗之基本架構如圖二。其後在1998年初，在義大利羅馬大學的研究團隊[5]應用兩個糾纏的光子，並把每個光子之兩個自由度，動量和極化態，一齊考慮進來，他們在一個光子上應用這兩個自由度建構了不同的貝爾態，而要傳輸的極化態是在其中一個光子上調出來的，他們成功地把極化態由一個光子傳輸到另一個光子上，這兩光子的傳輸裝置只能傳輸純態，非純態就無能為力了，同年年底，在美國加州理工學院由Jeff Kimble[6]領導的光學研究團隊發表了一個完全成功的量子隱形傳輸，只是他們用的不是三個或兩個光子而是幅射場(Radiation Field)，所用的狀態不是極化態或動量而是一致態(coherent state)，在他們的裝置下，可以測量所有的貝爾態，因此甲送進之狀態皆能傳輸到丙，傳輸機率為100%。
八、未來展望
以上實驗所完成的量子隱形傳輸都是在同樣的量子系統間傳輸狀態，而且用的量子系統都是光子(電磁場)，未來應可以發展到不同的量子系統，如電子，原子，分子，量子點等，而且不限於同樣量子系統間狀態之傳輸，我們如果能夠把一個不穩定或壽命短的系統上之資訊傳輸到一個穩定且壽命長的系統上，就能夠發展量子記憶(quantum memory)，當然我們都希望能像「航海家」星艦上一樣地傳輸人或實物，也許在遙遠的未來會成功，但是實体之傳輸應該完全不同於狀態之傳輸，其困難度是難於估計的，除此以外，量子隱形傳輸也預期將在量子電腦及密碼學方面扮演重要的角色。 走近量子纠缠-18-量子隐形传输（一）
精选
||
无论是量子信息、量子密码、量子计算等等，所有想要在计算或通讯中应用量子力学规律的领域，都离不开一个基本的位元：量子比特。从前面的章节我们已经了解到，量子比特是一个量子态，由于量子态的叠加性质，n个量子比特能够表示的状态数比n个经典比特能表示的状态数多得多，因此，量子比特比经典比特听起来更强大、更有用多了。不过，我们也知道，量子态是不确定的、难以对付的。除此之外，它还有个经典比特完全没有的性质：不可克隆定理。
量子态不可克隆定理说: 一个未知的量子态是不可克隆的。有学者在1982年（见参考资料）从量子态叠加原理的推论，而证明了这个定理。在此，我们只是从测不准原理来粗浅地理解这个定理：从经典‘克隆’的意义上说，要想精确地复制一个物品，首先就要得到（测量）这个物品的所有的信息。然而，对一个遵循量子规律的系统（比如量子比特），我们不可能同时精确测量它的所有物理量，因为根据“海森堡测不准原理”，在同一时刻以相同精度测定量子的位置与动量是不可能的，我们只能精确测定两者之一。
从量子论的观点而言，测不准原理应该被称为“不确定性原理”更恰当一些。但如果使用经典的图像来想象微观世界的话，叫做“测不准”可能还更容易理解。比如，以测量电子为例，所谓测量，一定要使用测量方法和工具，要对电子进行测量，最好的方法就是使用激光去与电子相互作用。原子中的一个电子，从经典角度看，它的运动轨道是如此之小（10-10米），它的运动速度又是如此之快（106米/秒），在这种快速运动情形下的电子，被测量它的光子顶头一撞，速度和位置都全变了，又怎么可能测得准呢？
比如说，利用光被电子散射，可以测量电子的位置，但不可能将粒子的位置确定到比光的波长更小。所以，要想将位置测量准确，必须用更短的波长的光，而波长更短的光子具有更大的能量，就对电子的速度产生更大的扰动，使得速度更不能测准，反过来说也是一样。
“量子不可克隆定理”，是指在不知道量子状态的情况下复制单个量子是不可能的，因为要复制单个量子就只能先作测量，而测量必然改变量子的状态。我们在介绍量子比特时提到过，一个qubit有两个自由度，由于测不准原理的限制，我们无法准确地测量这两个自由度，因此也就无法精确地克隆出这个量子比特的状态。
量子态不可克隆，这是在通讯中使用量子比特的极大优越性。这个优点保证了量子密码、量子通讯的安全性。但是，也由此而为它在通讯上的真正应用设置了难以逾越的障碍。在我们现代社会中铺天盖地的通讯网中，每秒钟都在复制、传输着天文数字个比特的信息。仅拿一台ADSL上网的计算机来说吧，如果网速是512Kbps，那就是每秒钟传输51.2万个比特。可是，量子比特怎么办呢？连复制都不行，如何传输呢？
科学家总能想出一些窍门，不能克隆没关系，我们照样传输它们！这就是近年来在这个行业内热门的话题，叫做“量子隐形传输”。
美国的国际商业机器公司（IBM）不愧是计算机行业的龙头老大，它不仅引领着传统的经典计算机的研发和制造，在量子计算机的研究方面，几十年来也独树一帜，不论在理论方面，还是实验方面，都进行了大量的研究工作。比如上一节中提到过的“可逆计算” 的IBM科学家R. Landauer，他在1961年对“可逆计算”的研究就与量子计算机研究有关。
“量子隐形传输”的理论设想，是由另一位IBM研究中心的研究员，查尔斯·亨利·贝内特最先提出来的。贝内特1943年生于美国纽约市，既是一位物理学家，又是信息理论学家，是现代量子信息理论的开山鼻祖之一。
贝内特等提出“量子隐形传输”的六人团队
照片来自网络：http://researcher.ibm.com/view_project.php?id=2862
贝内特1970年从哈佛大学得到博士学位后，于1972年加入IBM的研究队伍。在IBM，他做了大量有关量子信息学方面的工作。他曾经提出对麦克斯韦妖的重新解释，他与同行们合作开发了BB84量子密码协议，并建立了世界上第一个量子密码的工作演示。
1993年，Bennett等六人团队，在“物理评论快讯”上发表文章，提出“量子态隐形传输”的设想。设想将一个未知量子态的完整信息，合作通过两个独立的通道（经典和量子）发送出去，在新的远离的位置重新组合后，产生一个在发送过程中被破坏了的原始量子态的精确副本。
贝内特等人的想法可由下图说明：
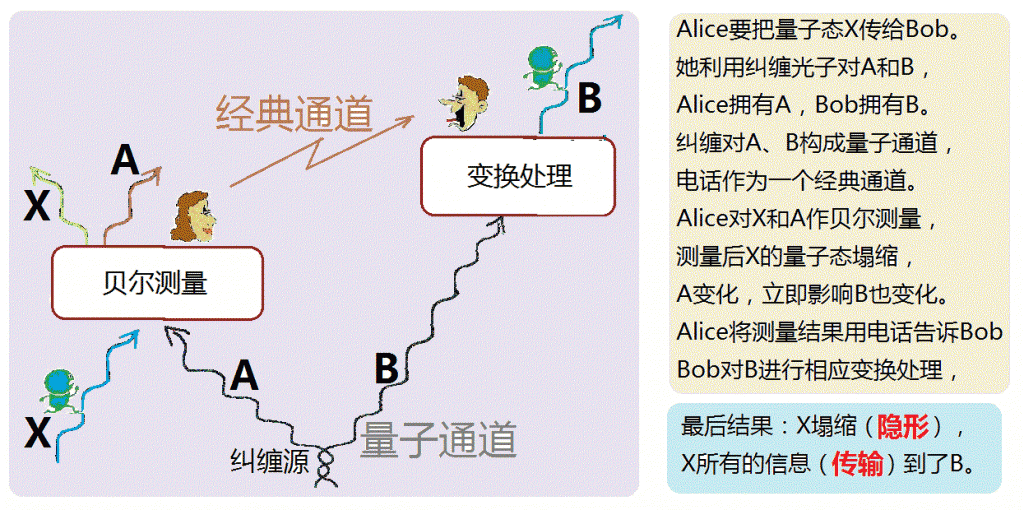
图中左边的Alice，想要把量子态X传给Bob。她利用纠缠光子对A和B，Alice拥有纠缠光子中的A，而Bob拥有B。纠缠光子A、B构成量子通道，电话或是互联网可作为经典通道。首先，Alice对需要传送的X和她手中的A作“贝尔测量”。测量后，X的量子态塌缩了，A也发生变化。因为A和B互相纠缠，A的变化立即影响B也发生变化。然而，Bob无法察觉B的变化，直到从经典通道得到Alice传来的信息。比如说，Alice在电话中将测量结果告诉Bob。然后，Bob对B进行相应的变换处理。最后，B成为和原来的X一模一样。这个传输过程完成之后，X塌缩隐形了，X所有的信息都传输到了B上，因而称之为“隐形传输”。
读者从上面的说法中，可能会提出以下几个问题：
1。既然是仍然要使用经典的通道，那为何还要量子通道呢？用经典通道把全部信息都传过去好了。
2。在Alice这边的方框中，“贝尔测量”是什么意思？
3。在Bob那边的方框中，“变换处理”是什么意思？
提出第一个问题的人，一定是因为不记得“量子不可克隆定理”了！根据这个原理，我们是不可能得到量子态X的全部信息的，所以，从经典通道就不可能传递所有信息。实际上，我们可以用经典电传（FAX）的例子作比喻，就知道，要想得到经典物体的“所有信息”，是很困难的。
用电传机发送电传的过程，可以用上面量子隐形传输示意图简化，而得到如下图所示的“电传示意图”：
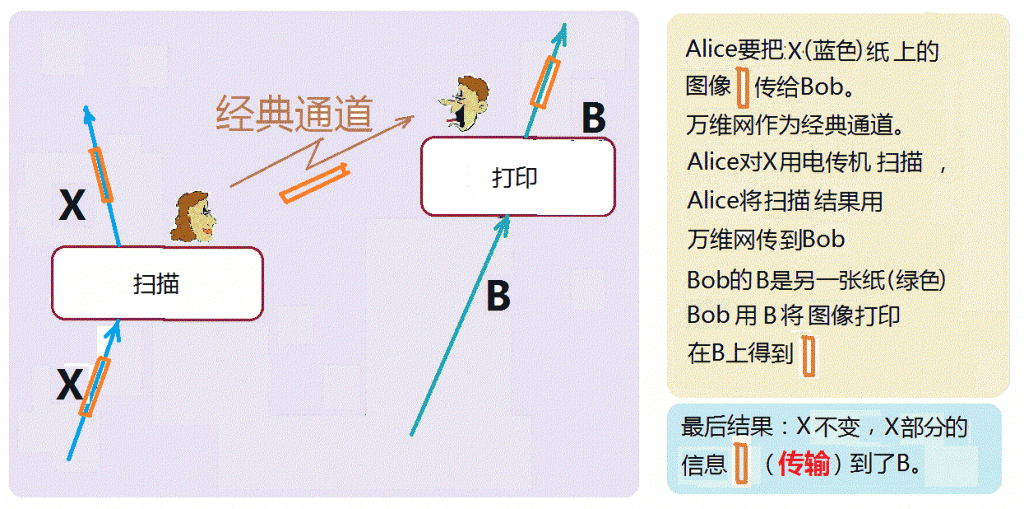
从上图看到，比之“量子隐形传输”，电传过程少了一个纠缠对构成的量子通道。在电传过程中，首先，Alice将上面印有图像信息的蓝色纸X进行扫描，得到需要传输的图像信息。然后，将此信息从经典通道（互联网）传给Bob。Bob收到图像后，用另外一张纸B（绿色）将图像打印出来。在这种传递过程中，“图像”只是X的一部分信息，X的其他信息，诸如纸张材料、颜色、大小、厚度等等，并不能从扫描过程得到，也没有被传递过去。况且，即使是Bob知道了这些性质，造出一张表面看起来完全一样的纸来打印图像，后来的B也不能说是和原来的X一模一样的。因为肯定不可能保证每个分子都一样吧。
而在量子隐形传输中，最后的B是和原来的X完全一样的。换言之，电传时传输后所复制出来的，只是纸上图像的信息，没有复制出任何‘实体’本身。量子隐形传输却有点像是：从得到实体的完整信息，而复制出了‘实体’本身，尽管只是一个小小的量子态！这样说，人们可能要心情激动、欢呼雀跃：“啊！科幻电影中远距离传物的时代就要来临了！” 其实远远不是这样，那种想法是一个误解。我们这儿谈论的“复制”不过只是一个量子现象，完全不知道如何才能复制一个较大的、真正的物体。即使是海边一颗小小的沙粒的传输复制，也还相距十万八千里。
上面提到的与量子通道有关的“贝尔测量”以及“变换处理”，留到下节讲解。
参考资料：
量子不可克隆定理：Wotte rs W . K . and Zurek W . H ., Nature . 299 (1982 ) , 802
量子隐形传输：C.H. Bennett, G. Brassard, C. Crepeau, R. Jozsa, A. Peres, and W. Wootters, "Teleporting an Unknown Quantum State via Dual Classical and EPR Channels", Phys. Rev. Lett. vol. 70, pp 1895-1899 (1993)
http://blog.sciencenet.cn/blog-677221-550786.html 此文来自科学网张天蓉博客，转载请注明出处。
上一篇：走近量子纠缠-17-量子计算机
下一篇：走近量子纠缠（19）量子隐形传输（二）
走近量子纠缠（19）量子隐形传输（二） 精选
精选
||
在解释贝尔测量(Bellmeasurement)之前，首先复习一下介绍qubit时使用过的狄拉克符号，并且重温我们在第八节中提到过的贝尔态的定义。
对一个单光子的系统，考虑它所有的偏振态，可以表示为两个基态｜1＞和｜0＞的线性组合：｜A＞ = a｜1＞+b｜0＞。如果是两个光子的系统，就有4个基态：
｜11＞、｜10＞、｜01＞、｜00＞。 （19.1）
这个两光子系统的所有量子态都可以用这4个基底的线性组合来表示。此外，我们也可以采取另外一种基底，叫做贝尔态基底。这就如同在我们的3维空间中，我们可以将xyz坐标轴旋转成另外一套x’y’z’坐标轴一样。这样做的目的是将原来那套不纠缠的基底（19.1）换成4个纠缠态（贝尔态）作为基底。4个贝尔态在原来的（19.1）基底下，可以表示如下面的形式：
｜f+＞ =｜11＞+｜00＞ （19.2）
｜f-＞ =｜11＞-｜00＞ （19.3）
｜y+＞ =｜10＞+｜01＞ （19.4）
｜y-＞ =｜10＞-｜01＞ （19.5）
既然（19.2-19.5）是2粒子量子态态空间的基底，那么，所有2粒子的量子态就都可以表示成这4个贝尔态的线性组合，也就是这4个贝尔态的叠加态：
｜2粒子量子态＞ = B1｜f+＞ + B2｜f-＞ + B3｜y+＞ + B4｜y-＞ （19.6）
（19.6）中的B1、 B2、 B3、 B4为复数，它们绝对值的平方：|Bn|2，分别表示测量时，这个2粒子量子态塌缩到相应的贝尔态的几率。因此，所谓的Alice对两个光子作“贝尔测量”的意思，就是探测这个两粒子系统到底塌缩到哪一个贝尔态。
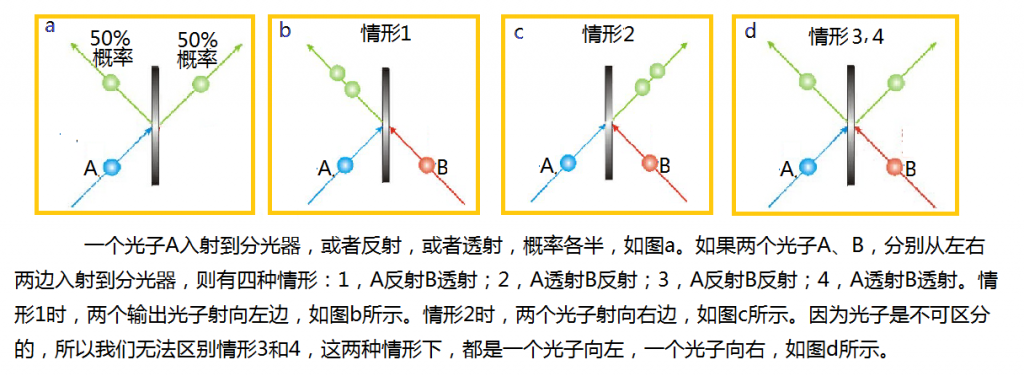
在实验室里，用作两光子贝尔态测量的主要设备是50:50分光器(beam splitter)。当一个光子经过分光器后，可能继续前进（透射），也可能被反射。光子走任何一条道路的几率是50%。这种分光器输出的各种情形如下图所示。
上图中的图a表示：一个光子A入射到分光器，或者反射，或者透射，概率各半。
现在考虑两个光子A和B，分别从左右两边入射到分光器。当两光子同时抵达分光器时，两光子之波包相互重叠，因而产生干涉效应。它们经过分光器后有四种情形：1，A反射、B透射；2，A透射、B反射；3，A反射、B反射；4，A透射、B透射。第一种情形，两个输出光子同时射向左边，如图b所示。情形2时，两个光子同时射向右边，如图c所示。但是，我们无法区别第三和第四这两种情形，因为光子是不可区分的。我们不知道，从分光器射出的光子，哪个来自A？哪个来自B？所以，在3和4这两种情形下，都是一个光子向左，一个光子向右，如图d所示。
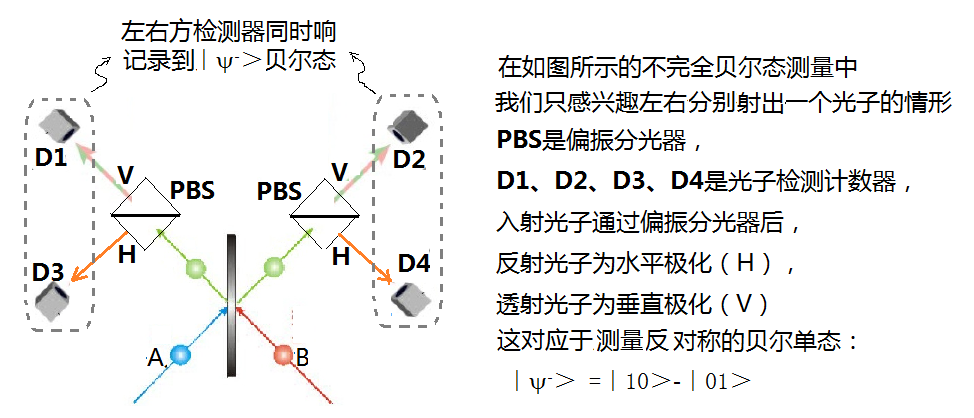
在此还必须说明一点：仅仅利用线性光学器件，不可能在实验中区分4个贝尔态。理论上已经证明，最多只可能区别4个贝尔态中的3个。所以，也就是说，如果只用线性元件，我们就只能作“不完全的贝尔测量”。在上面的公式（19.2-19.5）所表示的4个贝尔态中，｜y-＞ =｜10＞-｜01＞是一个反对称的单态，另外的｜f+＞、｜f-＞和｜y+＞则构成对称的三态。利用刚才所介绍的半透半反分光器，可以将贝尔单态｜y-＞，与其它贝尔态分开来。
如上图所示，在光子离开分光器(BS)出来的两个途径上各置一个偏振分光器（PBS）。光子经过PBS后，按概率分成垂直偏振和水平偏振两条路。左右两边的光子的两种可能性分别由侦测器D1、D3和D2、D4探测。我们仅仅当左右方两个检测器同时侦测到光子时，才作记录，这就是所谓的同时符合测量(coincidence measurement)。这样的设置意谓每一出来的途径必须有一个光子，所以只有两个可能：两个光子经过分光器时都继续前进或同时被反射，因为这两种情形是无法区分的，所以出来后之两光子态是这两种情形之状态之线性叠加，其振幅大小相同而符号相反。因此，在符合测量设置下，只有贝尔单态｜y-＞是容许的。这时，我们测量到了贝尔单态，而原来两光子之状态也崩溃成贝尔单态。
1997年，塞林格所领导的奥地利国际研究小组第一次在实验上实现了量子隐形传输。2004年，这个小组又利用多瑙河底的光纤信道，成功地将量子态隐形传输距离提高到600米。之后，中国科大——清华联合小组在北京八达岭与河北怀来之间，架设长达16公里的自由空间量子信道，并取得了一系列关键技术突破，最终在2009年成功实现了世界上迄今为止最远距离的量子态隐形传输。
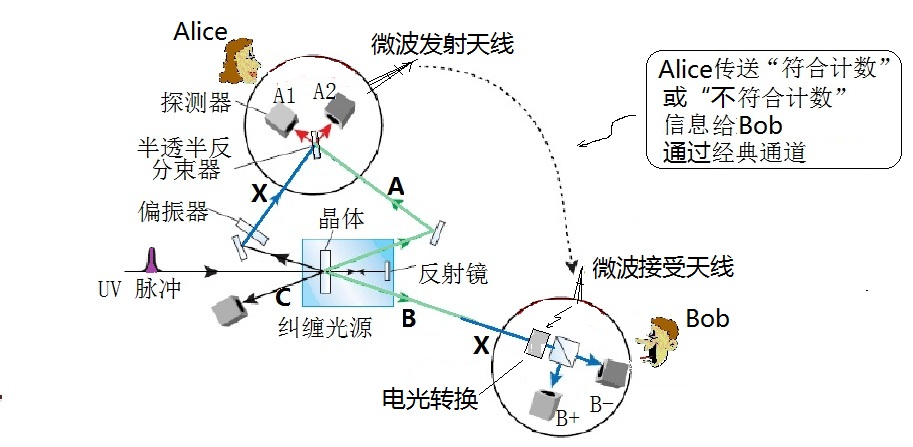
量子隐形传态实验过程的简化原理图如下所示：
图中心纠缠光源发出的孪生光子A和B分别传送给Alice和Bob。 Alice 处有半透半反分光器BS等，对A以及准备隐形传态的光子X，作刚才我们所描述的“同时符合”贝尔测量，将测量的结果：“符合”或“不符合”，通过经典通道，比如微波天线，发射给远在另一端（多瑙河对岸）的Bob。然后，Bob便需要对他所拥有的B，或者说是，从多瑙河底的光纤信道（量子通道）传过来的光子，作一些我们上一节中提到过的“变换处理”。
比较起Alice的“贝尔测量”来说，Bob的“变换处理”操作要简单多了，因为实际上，在Alice用X和A完成贝尔测量的那一霎那，X、A、B三粒子之间，已经完成了“纠缠转移”：原来不纠缠的X和A纠缠起来，光子X原来量子态的大部分信息，已经转移到B。比如在Alice作的“同时符合”贝尔测量情况下，Bob只需要根据从微波天线接受到的信息，对光纤信道传来的光子，作点小变换：如果微波信息是“符合”，什么也不作；如果微波信息是不“符合”，则将传来的光子的偏振方向变成与原方向垂直。上面所说的目的，用得到的微波信息，连到一个电光转换开关，再控制偏振器，即可达到。像在上图中，Bob的圆圈中所显示的那样。
到此为止，原来的光子X的所有信息都转移到了Bob所拥有的光子B上。而实际上，Alice和Bob从始至终都对X上的这些信息一无所知，他们唯一所知道的只是： 最后，X和A成为纠缠单态，Bob的粒子有了原来X的所有性质，隐形传态完成了。
在量子隐形传态的实验中，调节每个光子之间的时间差，做到两个光子必须“同时”到达测量仪器，对隐形传态的成功与否至关重要。
“贝尔测量”也是影响传态保真度的重要因素。因为利用线性光学元件，不能完全区分四个贝尔态。因此，要实现完全的贝尔测量，就需要采取另外一些办法。一个方法是使用非线性的光学器件（见参考资料）。
另外一条路就是采取“连续变量”纠缠源来实现量子隐形传态。
我们在此文中所叙述的量子纠缠及其在量子信息中的应用，基本是基于以单光子偏振态为代表的 “分离变量”方法。实际上，也有不少实验室研究所谓“连续变量”的量子信息技术。连续变量量子信息，是以光场正交振幅和正交位相分量为代表。“分离变量”对应于有限维的状态空间，可以用简单的量子力学算符和方程准确描述，而“连续变量”对应于无限维的状态空间，解释起来不容易。两种方式各有优点与不足，比如对量子隐形传态来说，用连续变量方法，可以做到完全的贝尔测量，理想情况下的贝尔探测效率可达100%。在此我们不多谈两种方式的优缺点，目前也有人提出hybrid 的方案，即是将分离变量和连续变量量子资源结合起来，发展混合型的量子信息技术。
可喜的是，对量子信息的研究和实验方面，中国的学者们，走在了国际科研的前沿。除了使用分离变量方法的中科大-清华团队之外，山西大学光电研究所在连续变量量子信息方面做了很多突出的工作，他们的实验室，不仅在国内连续变量领域是独此一家，在世界上也可算是这方面几个有代表性的实验室之一。他们在2004年，最早实现了连续变量的量子隐形传输。2006年，他们的研究团队利用连续变量量子纠缠，设计和实现了量子保密通信，并证明了它在长距离传输中的安全性（见参考资料）。
参考资料：
第一次量子隐形传态：D. Bouwmeester, J. W. Pan, K. Mattle, M. Eibl, H.Weinfurter, and A.Zeilinger, "Experimental quantum teleportation,"Nature 390 (6660),575-579 (1997).
中科大和清华团队文章：Xian-Min Jin, Ji-Gang Ren, Bin Yang, Zhen-Huan Yi,Fei Zhou, Xiao-Fan Xu, Shao-Kai Wang, Dong Yang, Yuan-Feng Hu, Shuo Jiang, TaoYang, Hao Yin, Kai Chen, Cheng-Zhi Peng and Jian-Wei Pan. ExperimentalFree-Space Quantum Teleportation，Nature Photonics, 4, 376-381(2010).
连续变量：“Experimental procedures for entanglementverification”, on Phys. Rev. A 75 , 052318 (2007)；
混合型量子信息：“Optical hybrid approaches to quantum information” on Laser & Photonics Reviews , February 25 , 2010。
连续变量量子隐形传输：Phys.Rev.Lett.93.250503;
连续变量量子保密通信：Europhys. Lett. 87, 20005 (2009); Phys. Rev. A 74,062305 (2006)。
（全文完）
No comments:
Post a Comment