1972年,克劳瑟和Freedman发表了他们用两百多个小时完成的实验,这实验之所以如此费时,也是因为当时的实验条件下,得到纠缠态粒子对太困难的缘故。那真的是百万里挑一的几率:每100万对光子中,可能只有一对,是能够成功地被观测到,对结果作出贡献的纠缠光子对。这点毛病不但拖长了实验的时间,也影响了实验的精度,被后来的实验者称之为“侦测漏洞”而提出质疑并加以改进。
有趣的是,这两个实验的结果,都和实验者的期待相反。克劳瑟希望量子力学输,他的实验结果却大大地违背贝尔不等式,以5倍于误差范围的偏离,强有力地证明了量子力学的正确!
||
话说当年,因为克劳瑟的宽阔胸怀,也因为他了解到波士顿的3个人已经开始计划真正的实验,因此他自己也迫不及待地想加入其中。最后,有关改良和验证贝尔不等式的这篇论文,以四位物理学家(CHSH)共同署名,发表在1969年的“Physics Review Letter”上。论文中改良了贝尔不等式,取消了几个关键的限制条件,并且重新设计了切实可行的实验方案。
我们再次把贝尔不等式写在这儿,以便大家思考:
|Pxz-Pzy| ≤ 1+Pxy。
这个式子中,有哪几个关键的限制条件需要改进呢?首先,上面的不等式中,有三个测量方向x、y、z。这三个方向是测量两个互为纠缠的粒子时共用的。而我们又希望在测量的时候,两个纠缠粒子分开得越远越好。远到一定距离就不太容易保证两边用的是同一个坐标系了。不是吗?让一对双胞胎远隔天边,他们就没办法互相丢眼色、弄虚作假啦。但是,两地离得这么远,总不能还使用同一套测谎仪,在两地之间运来运去吧。另外,贝尔在证明贝尔不等式时用的假设是自旋单态的完备相关,两个纠缠粒子需要准确地反向飞行。这些条件在真实的实验中也是不可能完全满足的。因此,CHSH的文章取消了Bell不等式需要的这些限制,重新推导出一个CHSH-Bell不等式:
|P(a1,b1)+P(a1,b2)+P(a2,b1)−P(a2,b2)|≤2。
这儿的P(ai,bj)表示相应的相关函数,在实验ai、bj中的统计平均值。
这个新不等式的相关实验,不像原来贝尔不等式那样难以实现了。改良推广了的不等式中,一对变量,也就是测量的方向 (a1,a2),可以在一个子系统上由爱丽丝完成,而另一对变量 (b1,b2)的 测量,在另一个子系统上由鲍勃完成。理论上说,这两个子系统可以位于空间分离相隔很远的地点。如果在以上的CHSH不等式中,假设体系总自旋为零,并且选取特殊情况的a1=b1,以及使用理想的反向关联函数:P(b1,b1)=-1, CHSH不等式就化简为原版的Bell不等式。

图一
在CHSH论文中的后半部分,作者提到用‘原子级联’的方法来生成验证Bell-CHSH不等式的纠缠光子对(图一),而不是用吴健雄那种正负电子对湮灭的方法。‘原子级联’的实验几年前曾经由加州柏克莱大学的科协尔和康明斯两人做过,并且也曾经测量过相关函数。但他们的测量数据不足以用来证明贝尔不等式,因为他们只测量了交角为0度和90度时候的相关函数值。而从我们在第7、8节导出贝尔不等式时就知道,根据量子力学,夹角为θ的两个不同方向上纠缠态粒子的关联函数平均值是(-cosθ)。因此,在0度、90度、180度等角度时的相关函数值,或者是-1,1,或者是0。在这些平凡情况下,量子论和经典论没有差别(见图二)。如下图中的红蓝两条曲线所示,经典理论和量子论预言的相关函数之差别很小,并且是在两个观测方向的夹角在0度和90度之间的那些角度,贝尔定理的实验验证,就是要测量出蓝色虚线相对于红色实线数值之差。

图二
在此也简单说明一下所谓‘原子级联’跃迁产生纠缠光子对的方法:比如,如图一所示,一个钙原子中的电子被紫外线袭击,有可能被激励到高出2个能级的状态。然后,当能量回落时,就有可能连续下降两个能级而辐射出两个纠缠的光子(在钙原子的例子中,将辐射出波长分别为551nm的绿光光子和423nm的蓝光光子)。
需要提醒读者注意的是,上面图一的示意图中,我们只画出了一个钙原子、一个紫外线光子,激发一个电子,产生一对纠缠光子。这显然不是实验中的真实情况。实际上是一束紫外线打到一堆钙原子上,辐射出来的也是两束光,很多对纠缠光子。在测量相关函数时,需要对多个光子运用统计方法进行计算。以后谈到实验时,也都是说的这种统计的测量和计算效应,特此表明,不再赘述。
无论如何,克劳瑟发现,要证明贝尔不等式,柏克莱大学科协尔和康明斯的实验数据还不足够,但是他们的方法却是非常可取的。于是,克劳瑟心急如火,想尽快做出这个实验,便立刻写信给他的祖师爷汤斯,申请柏克莱大学博士后的工作。他如愿以偿,汤斯接受他做博士后,进行有关射电天文学的观测研究。汤斯毕竟是得过诺贝尔奖的大师级人物,眼光不凡,远见卓识,还同意克劳瑟在做射电天文的同时,分出一半时间来做验证贝尔不等式的量子力学实验。不过,当克劳瑟到达柏克莱时,科协尔已经离开,康明斯还在那儿。但是,康明斯对验证贝尔不等式之事不感兴趣。最后,还是由汤斯出面,提议康明斯让一个研究生帮助克劳瑟工作。这样,克劳瑟才和Freedman一起,开始了他的实验。
如此一来,原来的四人小组CHSH在进行实验时,开始分道扬镳了:克劳瑟和Freedman在美国加州柏克莱大学实验室,背后有西摩尼和霍恩的支持。而哈佛的霍尔特,则从‘四人小组’中脱身出来,继续在波士顿的哈佛进行自己的实验,作为他PHD博士论文的课题。天下之事,分久必合,合久必分,科学家们之间也是如此。于是,这四个原来的合作伙伴,分别在美国东西两岸拉起队伍,暗暗地展开了竞争。
这四个人又如何预料和期待他们的实验结果呢?
克劳瑟是一个热情洋溢、活泼外向的年轻人。和贝尔一样,更相信爱因斯坦的隐变量解释,非常希望自己实验的结果能有助于找出量子论中的隐变量,引起物理理论的大革命。他用当时看起来数目不小的一笔钱(据说是500美元)与一个朋友打赌,赌隐变量理论赢,量子力学输。霍恩没有和人打赌,但认为量子力学会赢,因为他觉得这个古怪的量子力学总是赢!老练的西摩尼则不表态,说只能让实验结果说的话才算数。在哈佛大学单枪匹马战斗的霍尔特,则认同哈佛当时大多数物理学家相信的正统观点,希望自己的实验结果能成为量子力学完备性强有力的证明。
1972年,克劳瑟和Freedman发表了他们用两百多个小时完成的实验,这实验之所以如此费时,也是因为当时的实验条件下,得到纠缠态粒子对太困难的缘故。那真的是百万里挑一的几率:每100万对光子中,可能只有一对,是能够成功地被观测到,对结果作出贡献的纠缠光子对。这点毛病不但拖长了实验的时间,也影响了实验的精度,被后来的实验者称之为“侦测漏洞”而提出质疑并加以改进。
有趣的是,这两个实验的结果,都和实验者的期待相反。克劳瑟希望量子力学输,他的实验结果却大大地违背贝尔不等式,以5倍于误差范围的偏离,强有力地证明了量子力学的正确!
几乎同时,霍尔特也得出了他的实验结果,但他保持沉默不作声,迟迟没有发布他的结果。他的结果与他的期待不一样,没有违背CHSH-贝尔不等式,好像是支持隐变量理论的,这令相信量子论的霍尔特心中忐忑不安。当然,使得霍尔特犹豫不言的主要原因,是因为他的实验结果看起来非常勉强。在上面的CHSH-贝尔不等式中,不是要求两地所测的四个关联函数之和≤2吗?而霍尔特的结果小于2,又很靠近2。因此,他相信实验中一定有什么地方不对头,影响了观测结果。霍尔特的实验也是使用原子级联的方法来产生纠缠光子,但是,他不是用钙原子,而是使用汞。后来,有人找出了他实验中的问题,重新用汞做了这个实验,仍然得到了支持量子论的结果。
之后,接连又有好几个实验小组,包括吴健雄的实验室在内,都进行了检验贝尔不等式的实验,结果全都证明了量子力学的正确性。
不过,大家公认的对量子力学非定域性的最后实验判决,却是到了80年代初,由一位法国物理学家阿斯派克特作出的。
走近量子纠缠(19)量子隐形传输(二)  精选
精选
||
在解释贝尔测量(Bellmeasurement)之前,首先复习一下介绍qubit时使用过的狄拉克符号,并且重温我们在第八节中提到过的贝尔态的定义。
对一个单光子的系统,考虑它所有的偏振态,可以表示为两个基态|1>和|0>的线性组合:|A> = a|1>+b|0>。如果是两个光子的系统,就有4个基态:
|11>、|10>、|01>、|00>。 (19.1)
这个两光子系统的所有量子态都可以用这4个基底的线性组合来表示。此外,我们也可以采取另外一种基底,叫做贝尔态基底。这就如同在我们的3维空间中,我们可以将xyz坐标轴旋转成另外一套x’y’z’坐标轴一样。这样做的目的是将原来那套不纠缠的基底(19.1)换成4个纠缠态(贝尔态)作为基底。4个贝尔态在原来的(19.1)基底下,可以表示如下面的形式:
|f+> =|11>+|00> (19.2)
|f-> =|11>-|00> (19.3)
|y+> =|10>+|01> (19.4)
|y-> =|10>-|01> (19.5)
既然(19.2-19.5)是2粒子量子态态空间的基底,那么,所有2粒子的量子态就都可以表示成这4个贝尔态的线性组合,也就是这4个贝尔态的叠加态:
|2粒子量子态> = B1|f+> + B2|f-> + B3|y+> + B4|y-> (19.6)
(19.6)中的B1、 B2、 B3、 B4为复数,它们绝对值的平方:|Bn|2,分别表示测量时,这个2粒子量子态塌缩到相应的贝尔态的几率。因此,所谓的Alice对两个光子作“贝尔测量”的意思,就是探测这个两粒子系统到底塌缩到哪一个贝尔态。
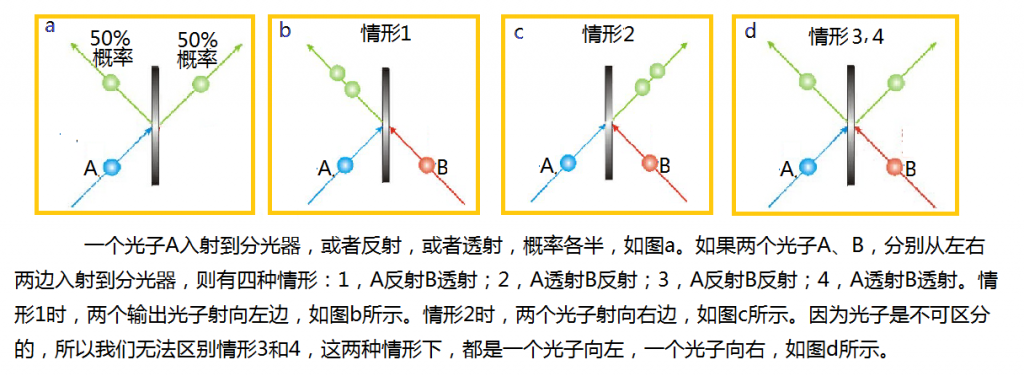
在实验室里,用作两光子贝尔态测量的主要设备是50:50分光器(beam splitter)。当一个光子经过分光器后,可能继续前进(透射),也可能被反射。光子走任何一条道路的几率是50%。这种分光器输出的各种情形如下图所示。

上图中的图a表示:一个光子A入射到分光器,或者反射,或者透射,概率各半。
现在考虑两个光子A和B,分别从左右两边入射到分光器。当两光子同时抵达分光器时,两光子之波包相互重叠,因而产生干涉效应。它们经过分光器后有四种情形:1,A反射、B透射;2,A透射、B反射;3,A反射、B反射;4,A透射、B透射。第一种情形,两个输出光子同时射向左边,如图b所示。情形2时,两个光子同时射向右边,如图c所示。但是,我们无法区别第三和第四这两种情形,因为光子是不可区分的。我们不知道,从分光器射出的光子,哪个来自A?哪个来自B?所以,在3和4这两种情形下,都是一个光子向左,一个光子向右,如图d所示。
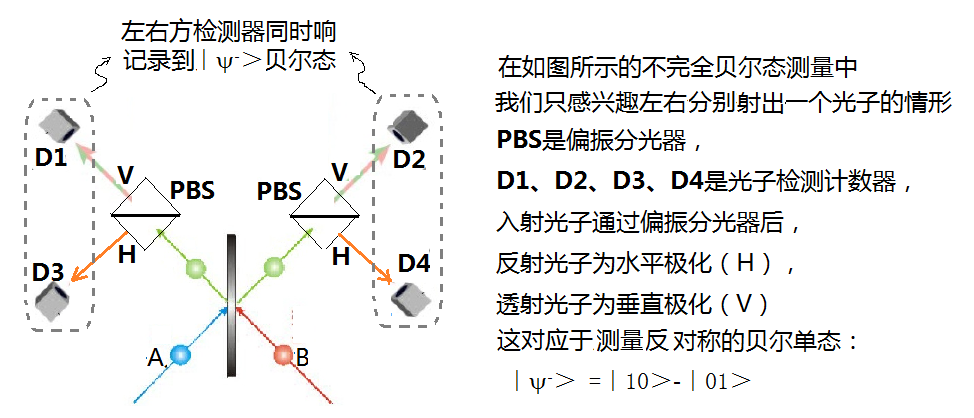
在此还必须说明一点:仅仅利用线性光学器件,不可能在实验中区分4个贝尔态。理论上已经证明,最多只可能区别4个贝尔态中的3个。所以,也就是说,如果只用线性元件,我们就只能作“不完全的贝尔测量”。在上面的公式(19.2-19.5)所表示的4个贝尔态中,|y-> =|10>-|01>是一个反对称的单态,另外的|f+>、|f->和|y+>则构成对称的三态。利用刚才所介绍的半透半反分光器,可以将贝尔单态|y->,与其它贝尔态分开来。

如上图所示,在光子离开分光器(BS)出来的两个途径上各置一个偏振分光器(PBS)。光子经过PBS后,按概率分成垂直偏振和水平偏振两条路。左右两边的光子的两种可能性分别由侦测器D1、D3和D2、D4探测。我们仅仅当左右方两个检测器同时侦测到光子时,才作记录,这就是所谓的同时符合测量(coincidence measurement)。这样的设置意谓每一出来的途径必须有一个光子,所以只有两个可能:两个光子经过分光器时都继续前进或同时被反射,因为这两种情形是无法区分的,所以出来后之两光子态是这两种情形之状态之线性叠加,其振幅大小相同而符号相反。因此,在符合测量设置下,只有贝尔单态|y->是容许的。这时,我们测量到了贝尔单态,而原来两光子之状态也崩溃成贝尔单态。
1997年,塞林格所领导的奥地利国际研究小组第一次在实验上实现了量子隐形传输。2004年,这个小组又利用多瑙河底的光纤信道,成功地将量子态隐形传输距离提高到600米。之后,中国科大——清华联合小组在北京八达岭与河北怀来之间,架设长达16公里的自由空间量子信道,并取得了一系列关键技术突破,最终在2009年成功实现了世界上迄今为止最远距离的量子态隐形传输。
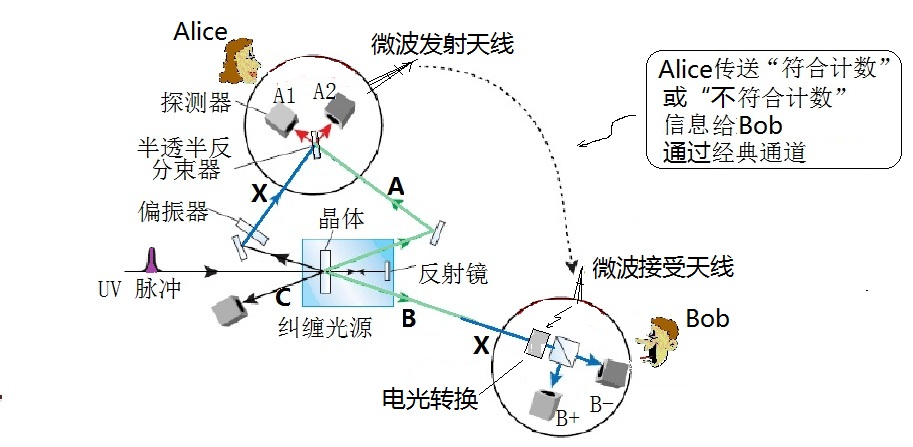
量子隐形传态实验过程的简化原理图如下所示:

图中心纠缠光源发出的孪生光子A和B分别传送给Alice和Bob。 Alice 处有半透半反分光器BS等,对A以及准备隐形传态的光子X,作刚才我们所描述的“同时符合”贝尔测量,将测量的结果:“符合”或“不符合”,通过经典通道,比如微波天线,发射给远在另一端(多瑙河对岸)的Bob。然后,Bob便需要对他所拥有的B,或者说是,从多瑙河底的光纤信道(量子通道)传过来的光子,作一些我们上一节中提到过的“变换处理”。
比较起Alice的“贝尔测量”来说,Bob的“变换处理”操作要简单多了,因为实际上,在Alice用X和A完成贝尔测量的那一霎那,X、A、B三粒子之间,已经完成了“纠缠转移”:原来不纠缠的X和A纠缠起来,光子X原来量子态的大部分信息,已经转移到B。比如在Alice作的“同时符合”贝尔测量情况下,Bob只需要根据从微波天线接受到的信息,对光纤信道传来的光子,作点小变换:如果微波信息是“符合”,什么也不作;如果微波信息是不“符合”,则将传来的光子的偏振方向变成与原方向垂直。上面所说的目的,用得到的微波信息,连到一个电光转换开关,再控制偏振器,即可达到。像在上图中,Bob的圆圈中所显示的那样。
到此为止,原来的光子X的所有信息都转移到了Bob所拥有的光子B上。而实际上,Alice和Bob从始至终都对X上的这些信息一无所知,他们唯一所知道的只是: 最后,X和A成为纠缠单态,Bob的粒子有了原来X的所有性质,隐形传态完成了。
在量子隐形传态的实验中,调节每个光子之间的时间差,做到两个光子必须“同时”到达测量仪器,对隐形传态的成功与否至关重要。
“贝尔测量”也是影响传态保真度的重要因素。因为利用线性光学元件,不能完全区分四个贝尔态。因此,要实现完全的贝尔测量,就需要采取另外一些办法。一个方法是使用非线性的光学器件(见参考资料)。
另外一条路就是采取“连续变量”纠缠源来实现量子隐形传态。
我们在此文中所叙述的量子纠缠及其在量子信息中的应用,基本是基于以单光子偏振态为代表的 “分离变量”方法。实际上,也有不少实验室研究所谓“连续变量”的量子信息技术。连续变量量子信息,是以光场正交振幅和正交位相分量为代表。“分离变量”对应于有限维的状态空间,可以用简单的量子力学算符和方程准确描述,而“连续变量”对应于无限维的状态空间,解释起来不容易。两种方式各有优点与不足,比如对量子隐形传态来说,用连续变量方法,可以做到完全的贝尔测量,理想情况下的贝尔探测效率可达100%。在此我们不多谈两种方式的优缺点,目前也有人提出hybrid 的方案,即是将分离变量和连续变量量子资源结合起来,发展混合型的量子信息技术。
可喜的是,对量子信息的研究和实验方面,中国的学者们,走在了国际科研的前沿。除了使用分离变量方法的中科大-清华团队之外,山西大学光电研究所在连续变量量子信息方面做了很多突出的工作,他们的实验室,不仅在国内连续变量领域是独此一家,在世界上也可算是这方面几个有代表性的实验室之一。他们在2004年,最早实现了连续变量的量子隐形传输。2006年,他们的研究团队利用连续变量量子纠缠,设计和实现了量子保密通信,并证明了它在长距离传输中的安全性(见参考资料)。
参考资料:
第一次量子隐形传态:D. Bouwmeester, J. W. Pan, K. Mattle, M. Eibl, H.Weinfurter, and A.Zeilinger, "Experimental quantum teleportation,"Nature 390 (6660),575-579 (1997).
中科大和清华团队文章:Xian-Min Jin, Ji-Gang Ren, Bin Yang, Zhen-Huan Yi,Fei Zhou, Xiao-Fan Xu, Shao-Kai Wang, Dong Yang, Yuan-Feng Hu, Shuo Jiang, TaoYang, Hao Yin, Kai Chen, Cheng-Zhi Peng and Jian-Wei Pan. ExperimentalFree-Space Quantum Teleportation,Nature Photonics, 4, 376-381(2010).
连续变量:“Experimental procedures for entanglementverification”, on Phys. Rev. A 75 , 052318 (2007);
混合型量子信息:“Optical hybrid approaches to quantum information” on Laser & Photonics Reviews , February 25 , 2010。
连续变量量子隐形传输:Phys.Rev.Lett.93.250503;
连续变量量子保密通信:Europhys. Lett. 87, 20005 (2009); Phys. Rev. A 74,062305 (2006)。
(全文完)
No comments:
Post a Comment