| | 今天我們所要討論的是一個跟數學與物理有關的題目,而這個題目如果從歷史上來看的話,它是來自於物理的,當然現在是屬於數學的範疇,我們現在就看一看。
第一個公式叫做Stokes'定理, 我們把它寫下來是這樣的一個公式:
上面這個公式, 一邊是線積分, 一邊是面積分, 所以我要假設各位已經有了線積分和面積分的基礎, 那麼這個公式是什麼意思呢? 就是說我們假設空間中有一個向量 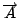 (如圖1) , (如圖1) , 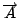 是隨著空間的點在變, 不同的點上有一個不同的向量, 這樣的東西我們就叫做一個向量場。 然後,我們隨便畫一個曲線 C,那麼我們就可以把這個向量場沿著這個曲線去做線積分,積完以後我們就得到一個值,這個值是等於什麼東西呢? 假如在這個曲線上,我們拿出一塊布把它蓋起來。造一個曲面,而以這個曲線為邊界。 我們現在就利用剛剛那個向量場來求一個叫做旋度(curl)的東西,它的公式是 是隨著空間的點在變, 不同的點上有一個不同的向量, 這樣的東西我們就叫做一個向量場。 然後,我們隨便畫一個曲線 C,那麼我們就可以把這個向量場沿著這個曲線去做線積分,積完以後我們就得到一個值,這個值是等於什麼東西呢? 假如在這個曲線上,我們拿出一塊布把它蓋起來。造一個曲面,而以這個曲線為邊界。 我們現在就利用剛剛那個向量場來求一個叫做旋度(curl)的東西,它的公式是
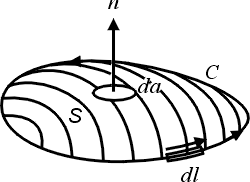
圖1 |
curl 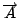 是由 是由 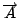 導出的另一個向量場。 其中 導出的另一個向量場。 其中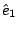 是指x軸, 是指x軸, 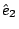 是y軸, 是y軸, 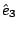 是z軸, 是z軸, 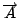 在x、 y、 z軸上的三個分量, 我們分別表示為A1、A2、A3, 它們都是函數, 因為 在x、 y、 z軸上的三個分量, 我們分別表示為A1、A2、A3, 它們都是函數, 因為 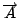 是隨著 x、y、z 在變, 所以 A1、A2、 A3當然也是函數。這裡我們為了等一下的理由把x、 y、z 改寫成x1、x2、x3, 然後把 是隨著 x、y、z 在變, 所以 A1、A2、 A3當然也是函數。這裡我們為了等一下的理由把x、 y、z 改寫成x1、x2、x3, 然後把 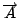 的分量A1、A2、A3 對x1、x2、x3 分別取導數, 再經過適當的運算,我們就得到一個由 的分量A1、A2、A3 對x1、x2、x3 分別取導數, 再經過適當的運算,我們就得到一個由 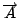 所導出的向量場, 當然, 在每一個地方都有一個curl 所導出的向量場, 當然, 在每一個地方都有一個curl 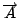 , 我們把每一點的curl , 我們把每一點的curl 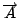 這個向量跟剛剛我們造的這個曲面當點上的法向量 這個向量跟剛剛我們造的這個曲面當點上的法向量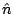 去做內乘(dot), 做完以後這也是一個函數, 在曲面上每一點都有一個值, 然後乘上曲面的面積元素da去做曲面積分, 所得到的結果和剛才的線積分相等, 這就是Stokes'定理。我們要注意一件事情, 這個曲面是任意的, 可以證明, 對於任意一個以這個曲線為邊界的曲面, 我們所做出來的積分值不變, 換句話說, 我們到底選擇什麼曲面並沒有關係。 底下我們再介紹另外一個定理, 我們叫做Gauss定理 去做內乘(dot), 做完以後這也是一個函數, 在曲面上每一點都有一個值, 然後乘上曲面的面積元素da去做曲面積分, 所得到的結果和剛才的線積分相等, 這就是Stokes'定理。我們要注意一件事情, 這個曲面是任意的, 可以證明, 對於任意一個以這個曲線為邊界的曲面, 我們所做出來的積分值不變, 換句話說, 我們到底選擇什麼曲面並沒有關係。 底下我們再介紹另外一個定理, 我們叫做Gauss定理
我們還是一樣在空間中有一個向量場 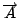 , 然後我們現在選一個封閉的曲面S, 一個封閉的曲面就會包圍一個體積V(如圖2) , 然後我們現在選一個封閉的曲面S, 一個封閉的曲面就會包圍一個體積V(如圖2)
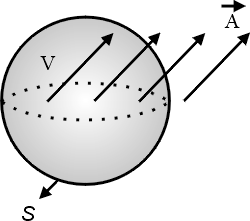
圖2 |
然後我們跟剛剛一樣在曲面上做曲面積分, 剛剛是用curl 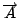 去做, 現在我們用 去做, 現在我們用 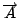 本身去做, 這個意義是完全一樣, 我這裡特別在積分符號上畫個圈, 只不過強調現在的S是一個封閉的曲面。 我們現在看右邊, 右邊是利用 本身去做, 這個意義是完全一樣, 我這裡特別在積分符號上畫個圈, 只不過強調現在的S是一個封閉的曲面。 我們現在看右邊, 右邊是利用 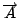 去做一個跟它相關的東西, 我們叫做散度(divergence), 用 去做一個跟它相關的東西, 我們叫做散度(divergence), 用 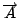 = = 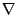  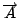 來表示, 剛剛我介紹的curl 來表示, 剛剛我介紹的curl 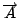 是一個向量, 現在所介紹的 是一個向量, 現在所介紹的  本身並不是一個向量, 而是一個數量函數, 它的定義是 本身並不是一個向量, 而是一個數量函數, 它的定義是
這個函數在V裡面每一點都有一個值, 然後乘上d3x這個小體積去做體積分, 結果我們得到邊界上的曲面積分等於裡面的體積分, 這就是Gauss定理。 Stokes' 定理與Gauss定理會成立的原因, 其實就是微積分基本定理(Fundamental Theorem of Calculus), 微積分基本定理是這樣的一個公式:
右邊是1-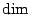 的積分, 左邊是0- 的積分, 左邊是0-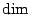 , 如果我們有一個線段, 它有兩個邊界a和b, 那麼點算是0- , 如果我們有一個線段, 它有兩個邊界a和b, 那麼點算是0-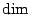 的東西, 所以左邊算是0- 的東西, 所以左邊算是0-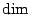 的一個量, 微積分基本定理就是函數在這兩個點上的值的差f(b)-f(a) 等於在這個線段上的這個函數導數的積分, 當然這個定理各位都很熟悉, 而事實上這個定理也是在所有數學中最重要的一個定理。這個定理我們有各種各樣的變形, 可以將它推廣到高維空間上面。現在我們看Stokes' 定理, 左邊是1- 的一個量, 微積分基本定理就是函數在這兩個點上的值的差f(b)-f(a) 等於在這個線段上的這個函數導數的積分, 當然這個定理各位都很熟悉, 而事實上這個定理也是在所有數學中最重要的一個定理。這個定理我們有各種各樣的變形, 可以將它推廣到高維空間上面。現在我們看Stokes' 定理, 左邊是1-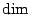 , 因為它是線積分, 在線上面做1- , 因為它是線積分, 在線上面做1-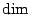 的積分, 等於一個2- 的積分, 等於一個2-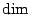 的積分, 而這個1- 的積分, 而這個1-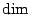 的積分區域是2- 的積分區域是2-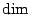 積分區域的邊界, 我們剛才所定義的curl 積分區域的邊界, 我們剛才所定義的curl 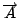 是 是 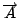 的一種導數, 所以右邊就變成一個函數導數的積分; Gauss定理也是同樣的道理, 所以這兩個定理只不過是微積分基本定理應用到1- 的一種導數, 所以右邊就變成一個函數導數的積分; Gauss定理也是同樣的道理, 所以這兩個定理只不過是微積分基本定理應用到1-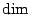 和2- 和2-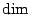 的關係、2- 的關係、2-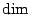 和3- 和3-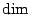 的關係而已。 其實這樣的定理有很自然的推廣,可以推廣到(n-1)- 的關係而已。 其實這樣的定理有很自然的推廣,可以推廣到(n-1)-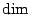 和n- 和n-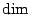 的關係, 當然我們必須要知道如何把curl和divergence的觀念推廣到n維的情況, 推廣出去之後的定理通稱為Stokes' 定理。 的關係, 當然我們必須要知道如何把curl和divergence的觀念推廣到n維的情況, 推廣出去之後的定理通稱為Stokes' 定理。
淺談 Stokes' 定理與電磁學 (第 2 頁) 邵錦昌
記錄:李啟鈴
| |
.原載於數學傳播第十八卷第四期
.作者當時任教於交大應數系
‧對外搜尋關鍵字 |
| |
我們這次討論的主要目的就是Stokes'定理與Gauss定理如何應用到電磁學上面, 然後得到電磁學的方程式, 就是Maxwell's equations, 所以我們來看一下電磁學在實驗上面、在觀察上面有那些基本的現象, 這些現象其實一共只有三個, 我們來看這三個實驗定律: | | |
| |
第一個實驗定律, 我們叫做Coulomb定律
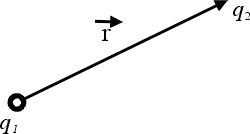
圖3 |
Coulomb定律也就是說如果有兩個電荷q1和q2(如圖3), 這兩個電荷中間有吸引力或排斥力, 相同的電荷相斥, 不同的電荷就相吸, 然後這個力量的大小和q1q2成比例, 且和反平方1/r2成比例, 而r就是q1 和q2的距離, 方向是在兩點的連線上, 如果把方向表示出來的話, 就變成 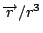 , q1、q2可正可負表示相斥或相吸。Coulomb 定律是在1785年左右, 由Cavendish 和 Coulomb 分別做實驗發現的現象, 所有的電磁現象的研究, 也就從這個年代開始。 , q1、q2可正可負表示相斥或相吸。Coulomb 定律是在1785年左右, 由Cavendish 和 Coulomb 分別做實驗發現的現象, 所有的電磁現象的研究, 也就從這個年代開始。 | | |
| |
第二個電磁現象, 我們叫做Biot-Savart 定律, 差不多是在1820年左右由Biot、Savart 及Ampere幾個人所發現的, 它的現象就是說, 假設有兩個線圈, 上面有電流通過, 一個是I1, 一個是I2(如圖4)
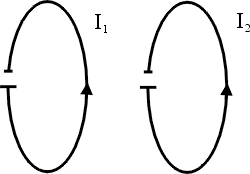
圖4 |
我們發現這兩個線圈中間也會有吸引力或相斥力, 這個現象我們叫做Biot-Savart定律。我們曉得電流是由電荷流動產生的, 這個力和庫侖力一樣也是由電荷產生的, 只不過它是由電荷的流動產生的, 雖然是由電荷產生, 但並不是電力, 而是一個新的力, 原因是如果我們把一個磁針放在線圈附近的話, 磁針會受到電流的影響, 產生偏移, 換句話說, 這個磁針會受到電流的作用力, 經由Biot、Savart和Ampere 等等長時間的研究後, 認為電流產生的力和磁針產生的力是同一性質的力, 並不是歸在剛剛我們所講的庫侖力, 這是一個新的力, 我們叫做磁力, 這個力的公式是這樣的:
這個公式要比當初庫侖定律複雜很多, 但基本上還是和反平方成比例。 | | |
| |
第三個定律叫做Faraday定律, 是在1831年由Faraday和Henry發現的。 假設我們有一個線圈, 然後我們讓磁場(稍後定義)在這個線圈附近變動(如圖5)
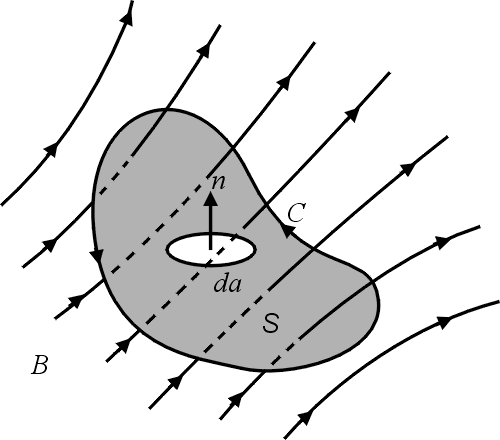
圖5 |
比如把一個磁鐵放在這個線圈裡面移動的話, 我們便會發現線圈中有電流通過, 所以, 磁場的變動就會產生電流,當然經過實驗之後, 它也可以歸納出一個定律出來, 這個定律可以寫成這個公式:
其中 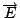 是指電場, 電場是由庫侖定律定義出來的。 是指電場, 電場是由庫侖定律定義出來的。 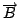 是指磁場, 將於稍後定義。如果這個線圈裡面有一個磁場通過, 把這個磁場對以這個線圈為邊界的曲面做曲面積分, 如果 是指磁場, 將於稍後定義。如果這個線圈裡面有一個磁場通過, 把這個磁場對以這個線圈為邊界的曲面做曲面積分, 如果 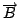 隨著時間變化, 當然積出來的量也隨著時間變化, 這時候, 這個變化率會產生電場, 這個變化率等於電場沿著線圈的積分值, 這就是 Faraday 定律。 這三個現象都是從自然界所發現的定律, 所有的電磁現象, 都是建立在這三個觀察現象上面(除了一點點重要的小修正外)。 隨著時間變化, 當然積出來的量也隨著時間變化, 這時候, 這個變化率會產生電場, 這個變化率等於電場沿著線圈的積分值, 這就是 Faraday 定律。 這三個現象都是從自然界所發現的定律, 所有的電磁現象, 都是建立在這三個觀察現象上面(除了一點點重要的小修正外)。
淺談 Stokes' 定理與電磁學 (第 3 頁) 邵錦昌
記錄:李啟鈴
| |
.原載於數學傳播第十八卷第四期
.作者當時任教於交大應數系
‧對外搜尋關鍵字 |
| |
Faraday 定律發現之後, 再經過一、二十年左右, Maxwell 把這三個 現象整理出四個方程式出來, 這就是有名的Maxwell's Equations, 最後就變成整套的電磁理論。 Maxwell's equation:
這四個方程式, 兩個是關於電場的divergence 和curl, 另外兩個是關於磁場的divergence和curl。所有的電磁現象, 例如:日光燈的發亮、 收音機、…等, 全部可以用這四個方程式來解釋, 這四個方程式是由先前的三個現象導出來的,導的過程主要是利用Stokes' 和Gauss定理, 還有一些向量的計算。導出這四個偏微分方程式之後, 剩下的問題,差不多就是數學家的問題。其中第一個方程式是和庫侖定律有關, 第三個是和Faraday定律有關, 剩下的兩個則是和Biot-Savart定律有關。 前面兩個式子很容易可以用Stokes';或Gauss定理導出, 比較麻煩的是由Biot-Savart定律導出另外兩個式子, 這裡我們要稍微提一下, Biot-Savart定律並不完全等於這兩個式子, 這中間還有一些需要討論, 所以在這三個實驗現象和Maxwell's Equations 之間還有一些東西需要補起來, 補這個東西的人當然就是Maxwell, 所以這些方程式,一般就叫做Maxwell's Equations。 那麼下面我們就開始用這三個現象, 經過Gauss和Stokes'定理來把Maxwell's Equations建立起來。 | | |
| |
| 3.1 從Coulomb定律到第一個Maxwell's Equation |
首先我們來看庫侖定律, 庫侖定律告訴我們, 如果我們有兩個電荷, 它們之間就有作用力, 而這個力符合反平方定律, 我們把這個公式寫得稍微詳細一點:
這個意思就是, 我們在空間中先選好一個座標原點, 再給座標 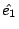 、 、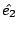 、 、 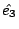 , 然後假設q1 是在 , 然後假設q1 是在 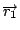 的位置上, 的位置上, 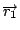 就是從座標原點到 q1 的位置, q2 是在 就是從座標原點到 q1 的位置, q2 是在 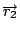 的位置上, 的位置上, 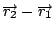 很容易可以看出來是q1 到 q2 的這個向量(如圖6) 很容易可以看出來是q1 到 q2 的這個向量(如圖6)
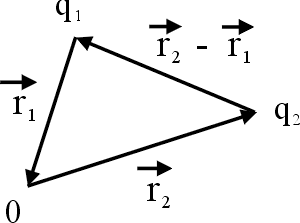
圖6 |
所以 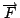 是指 q2 所受的力, 方向在 是指 q2 所受的力, 方向在 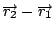 上, 大小是和反平方成比例。 上, 大小是和反平方成比例。 | | |
| |
3.1.1. 電場
為了研究方便起見, 我們不妨在(13)式中 q2 的位置放一個單位電荷, 因為所受的力與電荷大小成比例, 所以只要用單位電荷來研究就可以了, 放了單位電荷之後, 這個力我們就叫做電場, 電荷放在不同的位置, 電場的大小與方向也會變, 所以就把它看成是 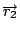 的函數, 然後將 的函數, 然後將 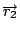 改寫成 改寫成 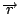 就得到 就得到
這就是電場的定義。如果我們在空間中多放一些電荷,根據實驗, 這些電荷作用在單位電荷上的力是遵守一個原理叫做 Linear superposition principle, 換句話說, 如果我們有電荷 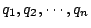 , 那麼這個單位電荷所受的力就是 , 那麼這個單位電荷所受的力就是
同樣地, 磁場也是遵守Linear superposition principle, 由於Maxwell's equations 要解的就是電場和磁場, 而我們出發點已經用了線性的原理, 所以我們得到的方程式都是線性的, 當然自然界的其它現象並沒有這麼簡單, 例如核子力就絕不是線性的, 所以現在物理學家所面對的問題是非線性的。 有的時候我們所討論的問題是一堆電荷可以像物質一樣, 而物質是由分子構成的, 不過分子很小, 當它很多又分佈的很密的時候, 我們可以用連續體的觀念來看它, 如果電荷也是這樣的話, 我們不妨介紹一個電荷密度ρ的觀念, 現在把qi用ρ表示, 和改成積分, 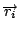 改成 改成 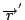 , 然後這個電場公式就是 , 然後這個電場公式就是
| | |
| |
3.1.2 推導過程
現在我們來求 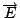 的divergence, 我們不妨以(15)式逐項來看, 經由直接計算, 我們很容易可以證明當 的divergence, 我們不妨以(15)式逐項來看, 經由直接計算, 我們很容易可以證明當 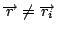 時, 時, 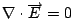 。然後我們把中間一個量拿來做面積分 。然後我們把中間一個量拿來做面積分
這個面Si怎麼取呢? 假設有很多個電荷 q1, q2,  , 對於qi電荷, 我們取一個以qi為球心的小球面(如圖7) , 對於qi電荷, 我們取一個以qi為球心的小球面(如圖7)
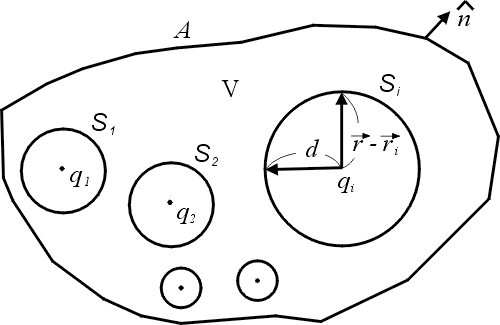
圖7 |
使得這個球只包含qi一個電荷,然後在球面上做面積分, 因為  在球面上, 那麼 在球面上, 那麼  就在 就在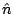 的方向上,假設球的半徑為d, 則 的方向上,假設球的半徑為d, 則
現在假設有q1,q2,…,qn個電荷, 然後做一個大體積V, 將所有的電荷都包含在裡面, V的邊界叫做A, 我們對 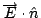 做面積分, 這個面積分等於每個小球面Si的面積分和 做面積分, 這個面積分等於每個小球面Si的面積分和
原因是如果將兩式相減, 這整個的積分可以看成是一個曲面S的積分, 現在的S就是把V扣掉各個小球之後, 所得到的體積V'的邊界, 然後根據Gauss定理, 這整個曲面上的積分,就會等於 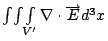 , 而在這個V'上的 , 而在這個V'上的 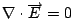 ,所以這個積分值就等於0, 移項之後就得到(18)式。又這些小球面上的積分等於 ,所以這個積分值就等於0, 移項之後就得到(18)式。又這些小球面上的積分等於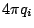 , 所以 , 所以  , 這就是有名的Gauss Law。 其實歷史上Gauss應該是先處理靜電學上的問題, 然後才把數學公式抽離出來,也就是Gauss定理。 剛剛我們處理的是一個一個的電荷, 現在把它推廣到有連續電荷分佈的狀況, 這時候電荷的和, 可以寫成 , 這就是有名的Gauss Law。 其實歷史上Gauss應該是先處理靜電學上的問題, 然後才把數學公式抽離出來,也就是Gauss定理。 剛剛我們處理的是一個一個的電荷, 現在把它推廣到有連續電荷分佈的狀況, 這時候電荷的和, 可以寫成 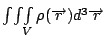 ,所以Gauss Law就變成 ,所以Gauss Law就變成
因為左邊是一個向量場的面積分, 我們可以再用一次Gauss定理, 它就等於 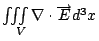 , 然後再前後對照一下, 因為這裡的A是任意取的, 所以 , 然後再前後對照一下, 因為這裡的A是任意取的, 所以 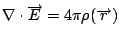 , 這就是第一個Maxwell's Equation。 , 這就是第一個Maxwell's Equation。 | | |
| |
| 3.2. 由 Biot-Savart 定律導出第二個和第四個 Maxwell's Equation |
接著我們再討論Biot-Savart定律, 這比較麻煩一點, 在討論之前, 我們先來介紹一下電流 | | |
| |
3.2.1. 電流
剛剛討論的是靜電學的東西, 也就是電荷靜止的狀況, 但是當然電荷也會動, 電荷動會有新的現象發生, 所以現在我們要考慮到電荷動的情況, 事實上電荷動的情形跟質點流動的情形一樣, 因此我們可以學習流體力學, 定義電流密度 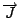 , , 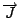 的方向在電流流動的方向 的方向在電流流動的方向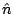 上, 如果N表示單位體積內的電荷個數, q表示每個電荷的電荷量, v是電荷速度, 則 上, 如果N表示單位體積內的電荷個數, q表示每個電荷的電荷量, v是電荷速度, 則
如果空間中有電荷在流動, 我們可以做一個小面積A(如圖8),
圖8

圖8 |
然後利用 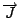 來求單位時間通過A的電荷量, 得到 來求單位時間通過A的電荷量, 得到
式中 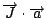 是 是 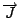 在法線方向上的分量。 一般而言, 我們平常用的電線的截面積A差不多都是相同的, 而且很小, 所以電線上的電流I=JA。 現在來看 在法線方向上的分量。 一般而言, 我們平常用的電線的截面積A差不多都是相同的, 而且很小, 所以電線上的電流I=JA。 現在來看 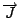 和ρ的關係, 因為我們總是假設電荷是保守的, 也就是電荷不會產生也不會消失, 所以假設空間中有電荷在流動, 取一個封閉曲面A(如圖9), 和ρ的關係, 因為我們總是假設電荷是保守的, 也就是電荷不會產生也不會消失, 所以假設空間中有電荷在流動, 取一個封閉曲面A(如圖9),
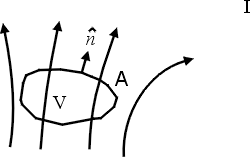
圖9 |
這時候A裡面的電荷量, 就等於 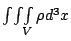 , 又因為電荷在流動, 所以這裡面的電荷量會改變,這變化的增加或減少, 完全是由於電荷的流進或流出, 這就可以用 , 又因為電荷在流動, 所以這裡面的電荷量會改變,這變化的增加或減少, 完全是由於電荷的流進或流出, 這就可以用 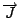 來算, 因此 來算, 因此
因為習慣上取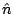 為向外的方向, 所以流出算正, 流入算負, 不過, 電荷量的導數, 增加時為正, 減少時為負, 所以上式中有一負號。 但是右邊又是一個面積分, 因此可以再用一次Gauss定理, 就得到 為向外的方向, 所以流出算正, 流入算負, 不過, 電荷量的導數, 增加時為正, 減少時為負, 所以上式中有一負號。 但是右邊又是一個面積分, 因此可以再用一次Gauss定理, 就得到 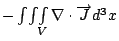 , 又A是任意取的, 所以等式對於任意V 都成立,於是得到 , 又A是任意取的, 所以等式對於任意V 都成立,於是得到
其實這個式子跟電磁學並沒有深入的關係, 只不過是一般的Conservation Law而已。 | | |
| |
3.2.2. Biot-Savart定律的討論
我們來看一下Biot-Savart定律為什麼是(7)式這種樣子, 作實驗時, 我們放兩個線圈I1和I2, 分取下一段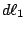 和 和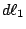 (如圖10) (如圖10)
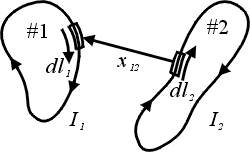
圖10 |
這兩段的電流是 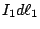 和 和 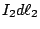 , 我們先看這兩個小電流中間的作用力, 這個作用力和 , 我們先看這兩個小電流中間的作用力, 這個作用力和 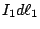 、 、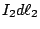 成比例, 這和剛剛靜電力與q1、q2成比例是一樣的, 所以 成比例, 這和剛剛靜電力與q1、q2成比例是一樣的, 所以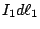 和 和 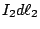 就是剛剛的q1和q2, 而 就是剛剛的q1和q2, 而 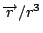 就是剛剛的反平方定律, 只不過方向比剛剛要複雜多了, 力的方向並不在兩點的連線上。 現在將 就是剛剛的反平方定律, 只不過方向比剛剛要複雜多了, 力的方向並不在兩點的連線上。 現在將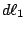 和 和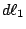 取下來看(如圖11) 取下來看(如圖11)
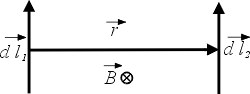
圖11 |
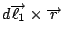 的方向指向紙內(利用右手定則), 我們將它定義成磁場 的方向指向紙內(利用右手定則), 我們將它定義成磁場 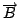 , 接著再看 , 接著再看 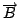 對 對 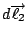 的作用, 如果我們做一個Biot-Savart定律的實驗, 將磁鐵放(如圖12) 的作用, 如果我們做一個Biot-Savart定律的實驗, 將磁鐵放(如圖12)
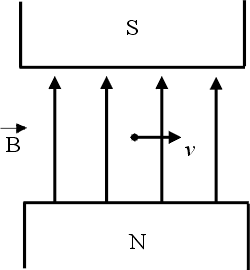
圖12 |
那麼就有一個磁場 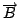 , 假如中間有一個電荷, 它靜止不動的話, 則它不受力, 若它在動的話, 它會受一個力, 這個力的方向和大小跟 , 假如中間有一個電荷, 它靜止不動的話, 則它不受力, 若它在動的話, 它會受一個力, 這個力的方向和大小跟 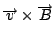 成比例, 所以力的方向與 成比例, 所以力的方向與 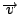 且與 且與 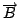 垂直。 剛剛我們已經定義了一個磁場 d 垂直。 剛剛我們已經定義了一個磁場 d 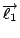 × × 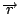 , 當然這個定義需要跟磁鐵做比較, 實驗的結果是一樣的, 而 , 當然這個定義需要跟磁鐵做比較, 實驗的結果是一樣的, 而 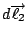 可以看成是一個電荷在運動, d 可以看成是一個電荷在運動, d 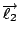 就像 就像 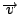 一樣, 所以最後的力就會與 d 一樣, 所以最後的力就會與 d 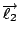 × × 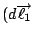 × × 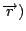 成比例, 再把這些小線段加起來, 就是這兩個線積分。 磁力和電力不大一樣, 磁力的方向並不在連線的方向上, 而在垂直的方向上, 所以磁力不作功, 而電力作功。 接著要把(7)式推廣到一般的情形, 因為我們要導一般電磁學的定律, 當然不能只用在線圈的電流上, 而是用在一般的電荷運動上, 首先, 我們研究所謂stationary的情形, 也就是電荷及電流不隨時間變動, 所以 成比例, 再把這些小線段加起來, 就是這兩個線積分。 磁力和電力不大一樣, 磁力的方向並不在連線的方向上, 而在垂直的方向上, 所以磁力不作功, 而電力作功。 接著要把(7)式推廣到一般的情形, 因為我們要導一般電磁學的定律, 當然不能只用在線圈的電流上, 而是用在一般的電荷運動上, 首先, 我們研究所謂stationary的情形, 也就是電荷及電流不隨時間變動, 所以 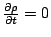 , 根據(22)式, 得到 , 根據(22)式, 得到 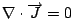 。 在一般的情形時, 因為I等於J乘上面積, 而面積再乘上 。 在一般的情形時, 因為I等於J乘上面積, 而面積再乘上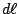 就變成體積分, 所以公式可以寫成 就變成體積分, 所以公式可以寫成
當我們在做Biot-Savart定律的實驗時, 因為一開始在Coulomb定律的時候, 就有電荷,從電荷又定義了電荷密度, 所以一切單位從這邊一直過來, 都已經固定了, 我們去量兩個線圈的作用力時, 發覺這個力相當的小, 所以當這些單位全部固定的時候, 有一個比例常數,實驗的結果它等於1/c2, c正好等於光速,因此這個力比靜電力小多了, 到目前為止, c與光速一致只是巧合而已。現在我們來看一下Biot-Savart 定律如何導出(10)和(12)式。 | | |
| |
第四個 Maxwell's equation 的導出
首先, 我們利用(23)式來定義磁場, 所以將 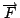 寫成 寫成
假設有兩堆電荷在流動, 一堆 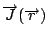 , 另一堆 , 另一堆 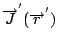 , 這兩堆流動的電荷就有作用力, 根據實驗的結果就得到(23)式, 然後把 , 這兩堆流動的電荷就有作用力, 根據實驗的結果就得到(23)式, 然後把 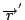 這部份的積分叫做 這部份的積分叫做 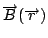 , 也就是 , 也就是 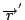 這部份電荷流動所產生的磁場, 它在 這部份電荷流動所產生的磁場, 它在 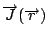 所做的力就是 所做的力就是 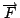 , 然後比較兩式, , 然後比較兩式,
這就是電流產生磁場的定義。底下我們用到一個公式
所以
然後我們再用一個向量的公式
我們把 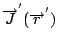 當成 當成 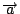 , ,  當成 ψ,但 當成 ψ,但 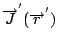 是 是 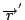 的函數, 而 的函數, 而 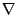 則是對 則是對 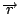 而言,所以 而言,所以 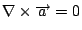 ,因此 ,因此 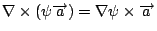 , ,
可是, 對任意向量函數 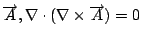 , 這一來的話 , 這一來的話 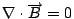 , 我們就得到Maxwell's equations 的第四個方程式。如果把 , 我們就得到Maxwell's equations 的第四個方程式。如果把 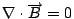 與第一個方程式 與第一個方程式 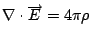 做比較的話, 我們可看出它的意義, 因為 做比較的話, 我們可看出它的意義, 因為 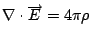 , 所以 , 所以 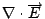 可以表示出電場的來源, 可是 可以表示出電場的來源, 可是 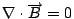 , 意思是說我們有electric charge, 可是我們並沒有magnetic charge。到了後來, 二十世紀的物理學家Dirac, 硬是要討論也有magnetic charge的情況, 這就是有名的monopole理論, 而且不管理論或實驗討論的非常多, 內容也很多, 但這是屬於另外的範圍。 , 意思是說我們有electric charge, 可是我們並沒有magnetic charge。到了後來, 二十世紀的物理學家Dirac, 硬是要討論也有magnetic charge的情況, 這就是有名的monopole理論, 而且不管理論或實驗討論的非常多, 內容也很多, 但這是屬於另外的範圍。 | | |
| |
3.2.4. 第二個 Maxwell's equation 的推導
現在我們來看第二個 Maxwell's equation, 利用(26)求 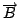 的 curl 的 curl
計算這個式子, 我們利用一個向量恆等式
其中
所以
我們先看第一項
接著再用另一個向量恆等式
我們把 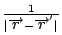 當做 ψ, 把 當做 ψ, 把 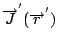 當做 當做 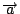 得到 得到
因為第一個積分是某一個向量場的 divergence 的積分, 這樣又可以用 Gauss 定理, 可是現在積分的範圍是任意的, 是包含所有電荷的任意範圍, 當然可以將這個範圍推到  去, 所以我們得到 去, 所以我們得到
這個面 S 可以推到  去, 而在 去, 而在  的地方,我們都假設物理量為 0, 否則,整個宇宙的能量會變成 的地方,我們都假設物理量為 0, 否則,整個宇宙的能量會變成  , 至於宇宙的能量我們相信是有限的, 所以(28) 式等於0, 而我們在做 Biot-Sovart 定律實驗時, 我們又假設了 stationary case, 因此, , 至於宇宙的能量我們相信是有限的, 所以(28) 式等於0, 而我們在做 Biot-Sovart 定律實驗時, 我們又假設了 stationary case, 因此, 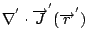 等於0, 我們就得到第一項整個等於0; 關於第二項, 我們使用底下這個式子 等於0, 我們就得到第一項整個等於0; 關於第二項, 我們使用底下這個式子
其中 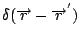 是所謂的 Dirac δ 函數,具有下面的性質,即對於任意函數 是所謂的 Dirac δ 函數,具有下面的性質,即對於任意函數 
其中 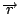 包含在體積 V 之內。關於這部份我們不說明得太詳細了, 總之 包含在體積 V 之內。關於這部份我們不說明得太詳細了, 總之
所以,就得到(27)式, 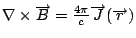 。這個式子和第二個 Maxwell's equation 有一些差別,這是最有趣的一部份,我們等一下再來談它。 。這個式子和第二個 Maxwell's equation 有一些差別,這是最有趣的一部份,我們等一下再來談它。 | | |
| |
| 3.3. 由 Faraday 定律到第三個 Maxwell's Equation |
根據實驗的結果, Faraday 定律是
又由 Stokes' 定理
比較上面兩式, 而且這個曲面 S 是任意的, 所以就得到第三個 Maxwell's equation
這一部份是相當簡單的。 | | |
| |
| 3.4. Faraday 的修正 Maxwell's Equation |
整個綜合起來, 我們差不多已經得到 Maxwell's equations 了。 可是比較一下我們所得到的四個方程式和Maxwell's equaitons,我們發現 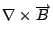 不一樣, 不一樣, 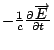 項沒有了,可以感覺的出來這四個方程式放在一起是不 consistent,因為只有一個跟時間有關的方程式, 別的方程式都沒有時間, 這很顯然一定有矛盾在, 所以我們知道的結果一定有缺陷, 因為我們在 Biot-Savart 的實驗時做了一個 stationary 的限制, 換句話說, 所討論的 項沒有了,可以感覺的出來這四個方程式放在一起是不 consistent,因為只有一個跟時間有關的方程式, 別的方程式都沒有時間, 這很顯然一定有矛盾在, 所以我們知道的結果一定有缺陷, 因為我們在 Biot-Savart 的實驗時做了一個 stationary 的限制, 換句話說, 所討論的 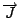 是加了 是加了 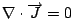 的條件進去, 因此所得到的定律本身有缺陷是很自然的, 這當然要靠Maxwell的天才, 他看出這個事實,然後把它補起來。 現在看 的條件進去, 因此所得到的定律本身有缺陷是很自然的, 這當然要靠Maxwell的天才, 他看出這個事實,然後把它補起來。 現在看  這個式子, 如果成立的話, 則 這個式子, 如果成立的話, 則
可是一般  。 為了要找出補救的辦法, 我們來考慮Conservation of charge, 這是一定會成立的, 所以 。 為了要找出補救的辦法, 我們來考慮Conservation of charge, 這是一定會成立的, 所以
Maxwell 覺得 ρ 可以由第一個方程式得到
因此
一般來講  , 除非stationary, 但 , 除非stationary, 但 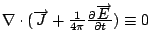 , 所以Maxwell就把 , 所以Maxwell就把 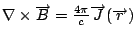 中的 中的 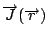 加上 加上 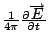 , 這時候 , 這時候 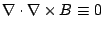 , 而 , 而 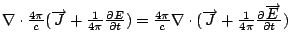 也恆等於0, 就把原來的第二個方程式修改成 也恆等於0, 就把原來的第二個方程式修改成
再把 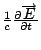 項搬到左邊, 於是得到我們要的第二個 Maxwell's equation。 Maxwell 只是做了這樣一個簡單的變動, 結果是對的, 所有的電磁現象全部在這裡, 也就是加了 項搬到左邊, 於是得到我們要的第二個 Maxwell's equation。 Maxwell 只是做了這樣一個簡單的變動, 結果是對的, 所有的電磁現象全部在這裡, 也就是加了 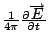 項之後, 我們由數學式子可以導出波動(wave)的現象, 可以導出輻射(radition) 的現象, 也就是一個電荷如果有加速度在動的話, 它會輻射出電波出來等等。 項之後, 我們由數學式子可以導出波動(wave)的現象, 可以導出輻射(radition) 的現象, 也就是一個電荷如果有加速度在動的話, 它會輻射出電波出來等等。
淺談 Stokes' 定理與電磁學 (第 4 頁) 邵錦昌
記錄:李啟鈴
| |
.原載於數學傳播第十八卷第四期
.作者當時任教於交大應數系
‧對外搜尋關鍵字 |
| |
現在再花一點時間說明一下波動現象, 我們看一下(11)、(12)這兩個方程式, 從 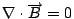 , 和剛剛所提一個東西的 divergence 如果等於0, 則它一定是一個curl, 所以 , 和剛剛所提一個東西的 divergence 如果等於0, 則它一定是一個curl, 所以 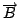 可以寫成 可以寫成 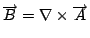 , 我們再看 , 我們再看 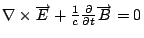 , 將剛剛的結果代入, 再把 curl 全部提出來, 得到 , 將剛剛的結果代入, 再把 curl 全部提出來, 得到 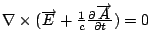 , 先前我們又提過, 一個東西的curl 等於0的話, 那麼它本身一定是一個gradient, 所以 , 先前我們又提過, 一個東西的curl 等於0的話, 那麼它本身一定是一個gradient, 所以 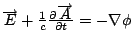 , 這裡的負號只是為了方便, 如此一來得到一組方程式 , 這裡的負號只是為了方便, 如此一來得到一組方程式
式中 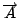 叫做 vector potential, 叫做 vector potential,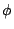 叫做 scalar potential, 我們將(29)、(30)代入(9)、(10)得到 A 和 叫做 scalar potential, 我們將(29)、(30)代入(9)、(10)得到 A 和 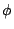 的方程式。 的方程式。
我們可以設法使  ,因為A和 ,因為A和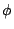 都並不唯一, 如果 都並不唯一, 如果 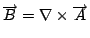 那麼另外一個函數 那麼另外一個函數  的curl也是等於 的curl也是等於 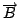 , 而如果 , 而如果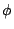 也同時換成 也同時換成 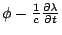 的話, 的話, 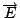 也不會改變, 所以我們總是可以選擇適當的λ, 使得 也不會改變, 所以我們總是可以選擇適當的λ, 使得  , 剩下的方程式, 就是所謂的wave equation, c是這個波的速度, 即波速, 實驗量出來的結果,c正好等於光速, 所以Maxwell就說光是一種電磁波, 當然Maxwell以前已經有物理學家說光是一種波動, 但是並不曉得光是電磁波, 所以Maxwell的發現, 當然是一種劃時代的發現。 , 剩下的方程式, 就是所謂的wave equation, c是這個波的速度, 即波速, 實驗量出來的結果,c正好等於光速, 所以Maxwell就說光是一種電磁波, 當然Maxwell以前已經有物理學家說光是一種波動, 但是並不曉得光是電磁波, 所以Maxwell的發現, 當然是一種劃時代的發現。
淺談 Stokes' 定理與電磁學 (第 5 頁) 邵錦昌
記錄:李啟鈴
| |
.原載於數學傳播第十八卷第四期
.作者當時任教於交大應數系
‧對外搜尋關鍵字 |
| |
由三個實驗定律最後能夠導出四個簡潔的方程式, 包含了所有的電磁現象, 這當然是經過很多偉大的天才, 在長時間的努力之下才完成的。但毫無疑問的Stokes'定理及
http://episte.math.ntu.edu.tw/articles/mm/mm_21_2_01/page6.html
推廣到三維空間:Gauss 定理與 Stokes 定理
從醉月湖的面積談起
向量微積分簡介 (第 6 頁) 蔡聰明
| |
.原載於數學傳播第二十一卷第二期
.作者當時任教於台大數學系
‧對外搜尋關鍵字 |
| |
| 6. 推廣到三維空間:Gauss 定理與 Stokes 定理 |
抓住了 Green 公式的形式與內涵,要推廣到三維空間就不難了。首先令
表示空間中的一個向量場 (Vector field),即定義在空間中某領域的一個向量值函數。
- 定義:
分別叫做向量場 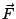 的散度與旋度。 的散度與旋度。
其次我們注意到,平面領域 Ω 可以有兩個方向的推廣:一個是空間中的可定向 (Orientable) 曲面 S(Möbius帶子就不是可定向曲面),參見圖16;另一個是空間中的一塊立體領域 V,參見圖17。
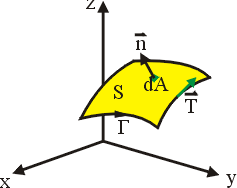
圖16 |
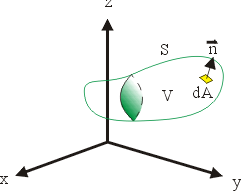
圖17 |
在(19)式中,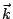 是 Ω 的向外單位法向量;當 Ω 改為空間曲面 S 時, 是 Ω 的向外單位法向量;當 Ω 改為空間曲面 S 時, 就應該改為 S 的向外單位向量 就應該改為 S 的向外單位向量 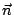 。 我們可以證明 。 我們可以證明 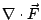 與 與 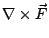 跟二維的情形有類似的解釋。 跟二維的情形有類似的解釋。 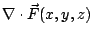 表示單位時間單位體積流體在點 表示單位時間單位體積流體在點 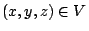 的流出通量, 的流出通量, 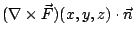 表示單位時間單位體積流體在點 表示單位時間單位體積流體在點  的循環量。從而(19)與(20)兩式就推廣為: 的循環量。從而(19)與(20)兩式就推廣為:
- 定理4: (Gauss 定理,又叫做散度定理,1839年)
- 設向量場
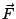 的分量 P,Q,R 及其一階偏導函數皆為連續函數,則 的分量 P,Q,R 及其一階偏導函數皆為連續函數,則
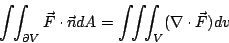 | (31) |
其中 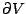 為圍成 V 之封閉曲面,dV 表示無窮小的體積元。 為圍成 V 之封閉曲面,dV 表示無窮小的體積元。
- 定理5: (Stokes 定理,又叫做旋度定理,1854年)
- 在與定理4相同的假設下,我們有
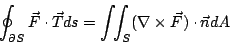 | (32) |
參見圖16。
在上述中,(31)式與(32)式分別將曲面積分與三重積分,線積分與曲面積分連結起來。若採用直角坐標系來表達,它們分別就是
以及
這一切可以再推廣到 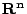 的可定向 k 維可微分子流形 的可定向 k 維可微分子流形  ,用微分式的積分與外微分理論,統合成為廣義的 Stokes 定理: ,用微分式的積分與外微分理論,統合成為廣義的 Stokes 定理:
 | (34) |
其中 ω 為 k-1 型微分式。這是微積分學根本定理最本質的形式。
学习外微分形式的一些感受
PB07210141 焦凡书
外微分形式把Stokes,Gauss公式联系起来,而且推广到高维空间。初学时觉得很“神奇”,查阅了一些书籍后才知道Poincare’指出多重积分的体积元素应有一个正负定向导致了外微分的出现。而外微分的出现可以说标志着微积分从古典走向现代。在物理,力学,偏微分方程,微分几何中,外微分发挥了巨大的作用。外微分有其更本质的含义,下面是我的一些总结和感受。
如果我们研究曲面(双侧曲面)的方向性,那么:在双侧曲面上任意取定一点M,并在M处选定一个单位法向量n(M),对于曲面S上任意一点M’,在S上做一条连接M,M’的曲线,由n(M’)沿曲线连续变化的原则,就可以唯一的确定M’处的单位法向量n(M’),从而就完全确定了双侧曲面的一个侧。曲面S在M处的单位法向量有且仅有两个,它们是互为相反方向的单位向量,这两个向量正好确定了曲面的两个定侧。
在双侧曲面内令:x=x(u,v) y=y(u.,v)
则面积元素dA=dxdy=|  |dudv=|  |dudv=(  )dudv
若将x,y 对换dA=dydx=|  |dudv=|  |dudv=(  )dudv
可得dxdy=-dydx
dxdx=0
我们把满足上述关系即:两个相同微分乘积为零,不同微分乘积变换顺序时变号的微分之间的乘积称为微分外积,用 表示。由微分的外乘积乘上函数组成的微分形式称为外微分形式。若 表示。由微分的外乘积乘上函数组成的微分形式称为外微分形式。若P,Q,R,H 是x,y,z 的函数,则Pdx+Qdy+Rdz 为一次外微分形式。Pdy  dz+Qdz  dx+Rdx  dy 为二次外微分形式,Hdx  dy  dz 为三次外微分形式。
可以证得(1 )Newton-Leibniz 公式用外微分表示 =f(b)-f(a)= 
(2 )Green 公式用外微分表示 Pdx+Qdy,  =  ,
(3 )Gauss 公式用外微分表示 Pdy  dz+Qdz  dx+Rdx  dy,  Pdy  dz+Qdz  dx+Rdx  dy=  dx  dy  dz, 
(4 )Stokes 公式用外微分表示 Pdx+Qdy+Rdz,  ,
而数量场的梯度,向量场的散度,旋度分别与之对应。因此他们的关系可以表示为
外微分形式的次数
|
空间
|
公式
|
对应的度
|
0
|
直线段
|
Newton-Leibniz
|
梯度
|
1
|
平面区域
|
Green
|
旋度
|
1
|
空间曲面
|
Stokes
|
旋度
|
2
|
空间区域
|
Gauss
|
散度
|
由此得出公式的一般形式:
G 是d  的积分区域, 的积分区域, G 表示G 的边界。
Stokes 公式揭示了微分与积分在空间上的关系。若令 , ,d 为算子,则它们对偶.
所以说Stokes公式是微积分中最本质的,由它引出了微分几何,广义相对论的很多内容,我的知识有限,希望以后有能力了解更多。
参考书目:《高等数学导论》
《微积分五讲》龚升
许小年中欧2015班委大会演讲实录
1)经济下滑,前几年透支的结果。
2)过去追求GDP用印钞、借债发展。地方债务风险,目前的政策,实际是用长债换短债,推迟还债时间。
3)中央银行为此背书,有可能买地方债务。中央政府不应再托经济,否则将经济转型后延,必须通过改革创造新的红利。
4)对于新常态提法赞成:不再以GDP为目标;不再用宏观政策维持GDP;通过改革创造新的红利。问题是:口号;可是旧思维又回来:财政又开始花钱(落在中央财政身上);又货币扩张(降息降准)。
5)财政带动民间投资。可是不能:原因是无处可投。增发货币都去股市了。原因是过剩经济。不是差钱,而是差可以挣钱的投资机会。
6)股市-羊毛长在猪身上。钱没有去实体而去股市。
7)要去过剩产能-敢投资-经营良好-收入增加
8)对外输出过剩产能-一厢情愿的想法。
东盟十国:2点3万亿美元。俄罗斯2万亿美元。巴基斯坦2千5百亿。中国十万亿。所以不能带动我们的经济体。
9)股市牛在转型、一路一带等等说法。荒谬离奇!这是吹着口哨走夜路给自己壮胆。不愿意再写文章批了。目前没有任何理论可以解释目前的股市疯狂。除了凯恩斯的动物精神。
10)想问:股市融的钱是否进入实体经济?放眼望去,没有比股市更赚钱的。股市融资降低企业的融资成本?公司财务基本原理:股本资金成本比债务资金成本高,因为承担更高经营风险。这种说法开玩笑。大家都把自己资金当成0成本资金。股市赚不到钱。因为拿钱走的从来没有想到给股民高的回报。人为扭曲,造成企业乱投资,造成过剩产能。
11)最后下场会很惨。这次股市狂潮,真的不知道如何收场。
12)目前两个一致:第一,大家都知道泡沫。分歧在于什么时候破。第二,每个人相信,破的时候,比别人跑得快。
13)不知谁出的主意。国人皆可杀之。上害领导下害黎民。
14)企业自己要思考:企业目前如何转型。不转型等死,转型找死(主要是不知道怎样转型)。
15)我们这个民族缺乏独立思维能力的民族。造成跟风。
16)造成企业转型的障碍:第一,过去的成功,希望过去的成功可以无限复制。(转型不是转行)过去很多成功要素是低成本扩张(人员、土地、技术)以及可以抢占的市场。但是这个时代已经结束了。抢占市场,已经没有未饱和的市场了。企业成功的关键是研发和创新。传统的思维方式和传统的商业模式。第二,机会主义心理。“风口上的猪都会飞”。不断有人问风口再哪里。如果你把自己讲到猪的水平我和你无话可说。“我发现平台拥挤不堪,但平台上空空如野”。第三,中国企业家群体缺乏个性的群体。中国是个从众的文化。缺少内心世界,或者是外界建立的。追求的是外界的承认而不是自己的成就感。从而使我们在创新方面落后。外界统一的评价体系,就会严重趋同企业家的行为。所以在风口上拥挤不堪,而没有风的地方就没有人。严重制约创新。中国企业家很少说我干这件事“cool”。
17)对于互联网的看法:1、冷淡的漠视到恐慌式的膜拜。2、互联网只是200年间新技术的一项。蒸汽机远远超过互联网,电力,内燃机,电脑,从来没听说过蒸汽机思维、电力思维。国外没有这说法。英文怎么翻译互联网思维?3、互联网是帮助转型的利器不是神器。
18)所谓互联网思维,一项项对照了下,几乎没有新东西。甚至是有错误的。1、你一定要做到单品海量。不错但片面。互联网有很强的规模经济效应。nothing new。规模经济效应是由成本结构决定的,固定成本比重越大,越强。规模越大成本越低。互联网一旦建立,所以边际成本几乎等于零。但是这不是唯一商业模式。还有一种商业模式:多品微量。因为需求的多样化。2、产品要做到极致。这是错的。是自杀行为。产品的品质要做到成本和效益的平衡点上。越到后边成本上升越快。做到比所有竞争对手好一点点就可以了。3、羊毛出在猪身上。有效但不要神化。早就有了。沃尔玛早就在做了。(供应商)4、平台战略,因为轻资产,不操心。式互联网优势,也不是特有。比如宝洁,雀巢。做的都是平台。5,互联网+。真正的课题:如何开发自己的产品;如何提高效率。线上到线下,互联网+;线下去线上,+互联网。取决于哪个效率高。亚马逊趋势是离开电商,去干云计算和平台。可能干不过沃尔玛。去年网上销售增长额第一次超过亚马逊。亚马逊20%来自于非主营,平台和云计算。收益率高。简单的、不大需要体验的商品,适合上线。亚马逊和沃尔玛,两者长期共存,在各自优势领域超过对方。
一个人要是口口声声说互联网思维,就是没有思维。
19)关于创造价值:1、提供新的产品和服务;2、以更低的成本提供已有的产品和服务。赚钱未必创造价值。但是利润不可持续。如果创造价值就一定会赚钱并持续。金融机构创造价值是赚的信息的钱。信息收集处理分析。P2P,创造价值了么?创造了一些价值,只是“介绍所”。怎么保证婚姻介绍的成功,如果能保证,就创造大的价值。对信用的建立评估是金融。阿里是最有可能的数据来做,资产总量才200亿。小菜一碟。因为数据远远不够。
20)康德:启蒙定义:启蒙就是有勇气运用自己的理性。
Value_at_risk
你拿披萨的方式,很可能是错的
高斯 曲面 曲率 平面 几何 几何学 空间 建筑 波形 建材 弯曲 波纹 强度 张力 拉力 双曲 抛物 受力
Aatish Bhatia 发表于 2014-10-17 17:30

( Ent/编译)我们都遇到过这种情况。你抓起一块披萨,正要一口吞掉的时候,披萨一下子软了,从你的指尖处耷拉了下来。披萨饼本身的结构强度不够高,无法支持整片的重量。也许下次应该少加点儿料?不用,无需绝望。
如果是是个吃披萨多年的老手,那你应该知道怎么对付这样的场景:只需把披萨弯成U形即可。(手头没有披萨?拿一张纸试验一下就好。)
 一张纸拿在手里就会耷下去,但弯曲握就能让它笔直。为什么呢?图片来源:Aatish Bhatia
这个披萨小窍门的背后,深藏着一项关于曲面的强力数学。这一数学发现如此绝妙,以至于它的发明人——数学天才卡尔·弗雷德里克·高斯(Carl Friedrich Gauss)——给它起了个拉丁文名叫Theorema Egregium,意思是“绝妙定理”。
拿一张纸,卷成圆柱形纸筒。你可能觉得显而易见,纸本来是平的,卷成筒就弯了,对吧?可是高斯不这么想。他想给纸的弯曲程度(“曲率”)下一个定义,让它不因你人工施加的弯曲而改变。
 图片来源:Aatish Bhatia
如果你放大去看一只生活在纸筒上的蚂蚁,这只蚂蚁可以走很多条不同的路线。它可以沿着弯曲道路横着走下去,画出一个圆;也可以沿着平坦路线竖着走,走出一条直线。或者它可以把两种方式组合起来,走一条螺旋。
高斯的天才在于,他想到把所有这些路线都纳入曲率定义里面。办法是这样的:从任何一点出发,找到这只蚂蚁能选择的最极端的两条路线——也就是最凹的和最凸的两条线。然后把它们的曲率乘起来。凸的路线曲率是正的,凹的路线曲率是负的,直的路线曲率是0。你得到的数字,就是那个点上的高斯曲率。
 图片来源:Aatish Bhatia
举几个例子吧。对于纸筒上的蚂蚁来说,最极端的两条路,一条是横着画圆,另一条就是竖着画直线。但是因为直线具有0曲率,所以乘起来总是得到0。照数学家的说法,纸筒是平的——它的高斯曲率就是0。这正是因为你能用平整的纸张卷出一个纸筒。
相反,如果蚂蚁活在一个球上,那么它就无法找到平坦的路线,每一条道路都会有一定程度的向外凸出,所以高斯曲率一定是个正的数。所以,球是弯的,而筒是平的。你可以把一张纸卷成一个筒,却永远不能卷成一个球。
 图片来源:Aatish Bhatia
高斯的绝妙定理就是:生活在曲面上的蚂蚁,根本不需要离开它就能知道曲面的曲率。只要测量一下距离,计算一下就行。顺便说,这也是为什么我们没有离开宇宙却能测量出我们的宇宙是不是平的(根据目前的观测来看,它是)。
但这个定理还有一个绝妙的结果: 你可以随意弯曲一个曲面,只要你不拉长、压缩或者撕裂它,高斯曲率一定不会变。因为单纯弯曲不改变其上的距离,所以不管怎么弯,上面的蚂蚁总会计算出同样的高斯曲率。
听起来可能有点儿抽象,但是这推论有十分紧贴现实的结果。把一个橘子切成两半,吃掉里面的东西,然后把剩下半个橘子皮放在地上,踩吧。皮永远不可能被踩扁成一个完整的圆。相反,它一定会裂开。这是因为球面和平面拥有不同的高斯曲率,所以不扭曲、不撕裂,是不可能把球面压平的。有没有试过给人寄篮球当礼物?包装纸会遇到完全一样的问题。不管你怎么弯曲一张纸,它总会留下一点点“平”的痕迹,所以最后只能得到皱皱巴巴一团糟。
 桔子皮不可能压成完整圆——因为球面和平面高斯曲率不同(而且桔子皮也没有什么延展性)。图片来源:Aatish Bhatia
这个定理的另一个推论是,平面纸上永远不可能画出准确的地图。很多常见世界地图投影方式能精确地保留角度,但是在面积上就有严重误差。 数学博物馆的推特指出,服装设计师也面临类似挑战——他们在平面上设计花样,却要符合弯曲的人体。
 每个红色圆圈的实际面积是相等的,但在地图上看起来就有很大的差异。图片来源:Stefan Kühn (左), Eric Gaba (右) / Wikimedia
那这一切和披萨饼有什么关系呀?是这样的:你拿起披萨之前,它是平的(数学上说,它的高斯曲率为0)。高斯绝妙定理指出,这片披萨必须有 至少一个方向永远保持平整——不管你怎么弯,它一定会留下一点“平”的痕迹。当这片披萨塌下去的时候,平的方向(红色箭头)是朝侧面的,这对吃掉它可没有什么帮助。但是如果你抢在它塌下去之前,先把披萨侧着捏弯,就迫使另一个方向只能保持平整——也就是对着你嘴巴的方向。还真是绝妙的定理呀。
 没想到几何学也能这么美味吧。图片来源:Aatish Bhatia
在一个方向上弯曲,来迫使它在另一个方向上保持平直。一旦你理解了这个点子,你就会到处都看到它。仔细看看一片草叶。它通常都是沿着中央叶脉弯曲的,这能帮助它维持笔直,不会软塌下去。工程师经常用弯曲来强化结构承载力。在马德里扎祖拉体育场,西班牙结构工程师埃杜拉多·托罗亚(Eduardo Torroja)设计了一套创新的混凝土屋顶,从边缘一直伸到看台上方,遮蔽了大片区域,而厚度只有几厘米。这其实就是披萨技巧。
 弯曲的草叶。图片来源:Dudley Carr / Flickr
 西班牙扎祖拉体育场。图片来源:Ximo Michavila
弯曲带来力量。想想看:你能站在一个空易拉罐上,它能轻松承载你的体重;可是易拉罐外壁的厚度差不多和纸一样薄。它的秘密就是它的弯曲。如果有人趁你站在上面的时候拿笔戳一下易拉罐,就能戏剧化地展现这一点——只需一个小凹坑,它就会在你脚下轰然崩塌。
 纸板箱里隐藏的秘密。图片来源:Craig Sunter / Flickr
但最日常的例子可能是无处不在的波形建材。世界上简直没有比纸板箱更无聊的东西,但是撕开一个这样的箱子,你会看到箱壁里一条熟悉的波浪曲线。这些皱褶在里面可不是为了好看,它们是一种天才的结构方式:让材料又薄又轻,又能坚硬到足以承担可观的重压。
 很多人小时候玩过的把戏:把一张纸折叠几次就能承载很大的重量,但它背后的数学可能你就想不到了。图片来源:Aatish Bhatia
波形金属板使用的也是同样的原理。这些不起眼的建材是纯实用性的体现,它们的形态和其功能完美契合;它们的高强度和相对低廉造价使其成为了整个现代世界的背景。
今天,我们就算看到这些波浪形金属板也几乎不会多想什么。但当它们诞生时,许多人把波形建材看成是奇迹材料。1829年,亨利·帕尔默(Henry Palmer)获得了波形建材的专利,他是一个英国工程师,负责建造伦敦码头。帕尔默建起了世界上第一个波形钢结构建筑——伦敦码头的松油棚屋。虽然它今天看来可能没什么了不起,但是听听当时的一家建筑学杂志是怎么描述它的吧:
不久前路过伦敦码头时,我们十分满意地发现,帕尔默先生新发明的屋顶已经得到了实际应用。……任何一个目光敏锐的人,路过的时候都不可能不被它的优雅和简洁所打动(虽然它只是个棚屋);而只要稍加思索,他们就会相信这一建筑的效率之高、经济之节约。我们认为,这是自亚当诞生以来,人类之手所建造的最轻又最结实(以其重量而言)的屋顶。若我们仔细观察(我们为了这一目的而爬过了各式各样的粘稠松油罐),会发现这一屋顶的总厚度绝对没有超过十分之一英寸!
这年头的建筑学杂志真是大不如前了啊。
虽然波形建材和易拉罐的强度可以很高,但有个办法让这些材料变得更强。想自己找到这个办法?去冰箱拿个鸡蛋出来。放在掌心,整只手握住鸡蛋,挤吧。(尝试这个的时候记得别戴戒指。)你会为它的强度而惊讶的。我就没法把鸡蛋握坏,哪怕用尽全力也没戏。(真的,谁试谁知道。)
 请务必在家中尝试一下——好吧,为了安全,别在电脑前尝试。图片来源:Aatish Bhatia
鸡蛋为什么这么强?易拉罐和波形金属板在一个方向上是弯的,另一个还是平的。这一弯曲让它们拥有了一定强度,但它们还是有可能被压成本来的平板。
相反,鸡蛋壳两个方向上都是弯的。这是它的关键。用数学语言表达,那就是这些双重弯曲的曲面拥有非零的高斯曲率。像我们先前遇到的橘子皮一样,这意味着它们不可能被压平,除非有撕裂或者拉伸——有高斯绝妙定理保证这一点。要打破一个鸡蛋,你必须首先弄出一个坑。等到鸡蛋失去了弯曲,也就失去了强度。
 图片来源:Owen Cliffe / Wikimedia
核电站冷却塔的象征性形状也在两个方向上利用了弯曲。这个形状叫做双曲面,能让所需的材料最少。正常的烟囱很像巨大易拉罐——结实是结实,但是很容易弯。双曲面形状的烟囱靠双向弯曲来解决这个问题,这样的弯曲方式能把形状“锁死”在空间中,提供额外的强度。
另一种得益于弯曲的形状是品客“ 薯片”,照数学家的说法,这是个双曲抛物面(hyperbolic paraboloid,舌头打结了没?)。
 图片来源:Aatish Bhatia
自然界运用这一形状的招数堪称脑洞大开。濑尿虾有一项臭名昭著的本领——动物界里最快的拳击手,它的一拳打出去的力道足以把着力点上的水蒸发掉,创造出冲击波和闪光。要想使出这死亡一击,濑尿虾使用了双曲抛物面形状的“弹簧”。平时它把弹簧压缩起来储存巨大的能量,然后一招之内释放出来。
西班牙-墨西哥建筑师菲利克斯·坎德拉(Félix Candela)很懂薯片形状的力量。坎德拉是托罗亚的学生,他的建筑将双曲抛物面带到了新的高度(字面意思)。当你听到“混凝土”这个词的时候,恐怕只会想到无聊透顶的方块建筑,但坎德拉却利用双曲抛物面盖起了巨大的建筑,使用的混凝土薄到不可思议。身为这一材料的真正大师,他既是极富创新的建筑者,也是结构艺术家。
 图片来源:Ciudad de las Artes y las Ciencias / Flickr
所以为什么薯片形状强度如此之高?这和它平衡张力与压力的方式有关。一切建筑都要支撑重量,最终将这些重量传递到地面上。这一传递可以靠两种不同方式完成:其一是压缩,拱顶就是纯靠压力而实现的例子;另一个就是拉伸,把一根锁链拎起来,它的每一环就都处于拉伸状态、受到张力。双曲抛物面结合了两种方式的优点。凹下去的U型部分处于拉伸状态,而凸起来的拱顶部分则是压缩,高斯绝妙定理则保证了任何一个地方的受力都会传递到四周——因为这是一个高斯曲率非零的曲面。只要你试图改变它的形状,就必须得连带压缩或者拉伸一整片区域才能让结果遵从高斯的律令;像纸张那样只弯曲一条线而不影响其他部分是不可能的。通过这样的双重弯曲,这一形状实现了张力和压力之间的精妙平衡,让它以很小的厚度就能实现惊人的强度。
通过弯曲来产生强度,这个想法塑造了我们所见的当代世界,而它的根源却来自万古不变的几何学。所以下一次你抓起一块披萨的时候,记得朝周围看看,欣赏一下这个简单的披萨小把戏背后的庞大遗产吧。(编辑:Calo)
参考资料
- Reid, Esmond. Understanding buildings: a multidisciplinary approach. MIT Press, 1984.
- Mornement, Adam, and Simon Holloway. Corrugated iron: building on the frontier. WW Norton & Company, 2007.
- Garlock, Maria E. Moreyra, David P. Billington, and Noah Burger. Félix Candela: engineer, builder, structural artist. Princeton University Art Museum, 2008.
Clifford 几何代数的基本观点
已有 743 次阅读 2015-3-25 12:04 |个人分类:生活点滴|系统分类:科研笔记
高斯认为:曲面上的曲线微分长度平方、曲面上曲线的弯曲量度(曲率)是曲面上的任意曲线的基本度量量,具客观性。这是物理性的,为整个曲面几何理论的要素。这里,最小的几何单位是微元曲线、及两条正交微元曲线所形成的微元面。这个几何是没有点概念的。因为点是空(0长度,0面积)。
Clifford 几何代数的基本观点就是:物理上有意义的流形变换是保证上面的两类量的客观不变性。
黎曼几何是取曲线微分长度平方的客观不变性,建立黎曼张量代数。而李代数是取曲线微分曲率为客观不变量条件下的张量,其理论基础可归入旋转不变群。群论的时髦是出于上面的背景。物理学上的运动:微元长度的变化(对称群);曲率的变化(旋转群)。反对称群(李群,微元长度为0)是旋转群的低阶逼近。
以对称群为主导的代数是:可易的。对于非对称群,其导出的代数系统是:不可易的。
在过去的一百来年里,数学家在群论上的开拓进取成就很大。但是,对物理学和工程科学而言,有两个致命缺陷:1。以点的概念(点群)为主导;2。只取两高斯不变量中的一个。从而,自身理论上的完备和优美是以脱离物理真实的理想化近似来实现的。这是哲学路线上的错误。
在苦苦作战百年后,梦回头,才意识到:这两类不变性要同时满足!这就是Clifford 几何代数进入基础物理学的客观背景。也就是回到了实事求是,以物理客观性为基准的轨道上来。这是哲学路线上的调整。
不依赖于点概念的几何也就基本上有了基本的理论框架。这是高斯曲面科学理念的回归。发达国家有部分科学家呼吁:在高中课程中,必须为大学学习Clifford 几何代数作必要的前期教学。如何做?他们还在思考。而他们还认为,大学的相关课程,尤其是物理学基础理论的课程,必须改为用Clifford 几何代数表述。少数名校已经是这样做了。
数学必须服从物理上的客观性,这条原则将在今后很长时间里主导基础科学的发展方向。这对工程科学是福音!因为,Clifford 几何代数是可以直观操作的,它再也不是那堆玄而有玄的、优美的、难于直观理解的、工程性操作起来难而又难的、公理化封闭体系。
我国是工程大国,如果要进入世界先进水平行列,Clifford 几何代数必须进入工程科学。但是,我认为,除非科学界出现实质性的变革,否则,这个机会我国学界抓不住,从而进入不了工程科学。
国外的大多数学者、大多数高校都在抵制Clifford 几何代数进教科书。但是,他们目前的选择并不代表科学的主流发展走向。然而,我国学界的从众心理决定了,我们参与抵制!尽管我个人不希望如此,但客观事实就是如此!
星星之火,可以燎原!我们无论如何抵制,消灭不了Clifford 几何代数成为基础科学理论主流表述工具的趋势。正如无论如何批相对论,无法阻止张量表述成为过去百年来基础科学理论主流表述工具的事实。
明智的选择是:以史为鉴!
|
|
|
|
|
|
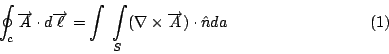
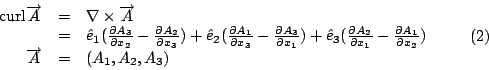
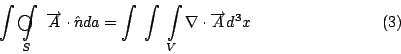





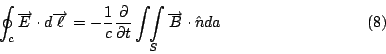
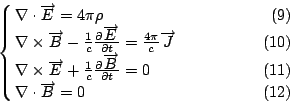


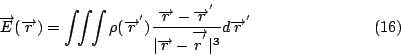
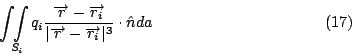

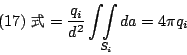
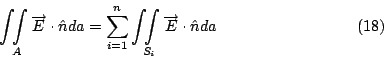
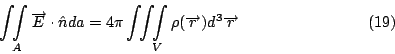

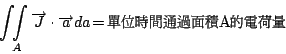

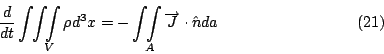



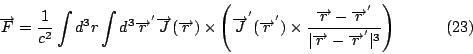
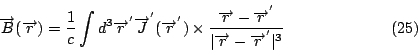
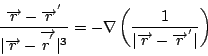
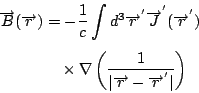

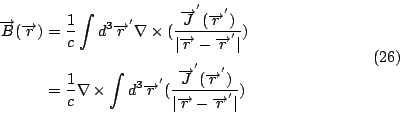
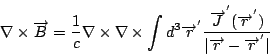
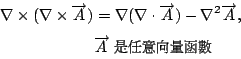
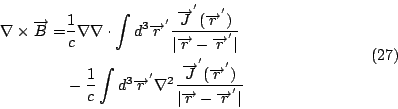
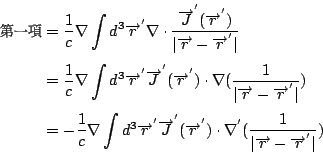
![\begin{displaymath}
\mbox{{\fontfamily{cwM2}\fontseries{m}\selectfont \char 15}\...
...vert\overrightarrow{r}- \overrightarrow{r}^{'} \vert}
\right]
\end{displaymath}](http://episte.math.ntu.edu.tw/articles/mm/mm_18_4_02/img102.gif)
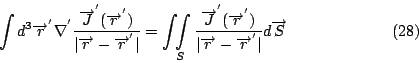
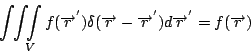
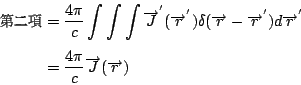
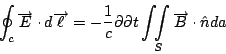
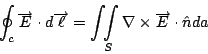
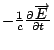
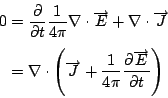
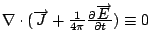
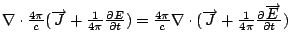
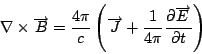
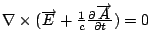
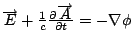


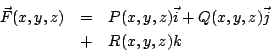
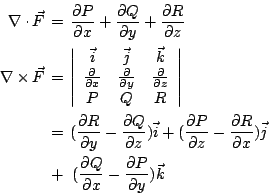


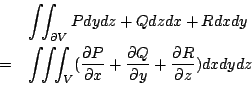
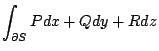
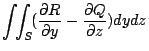
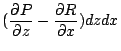
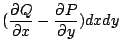

 一张纸拿在手里就会耷下去,但弯曲握就能让它笔直。为什么呢?图片来源:Aatish Bhatia
一张纸拿在手里就会耷下去,但弯曲握就能让它笔直。为什么呢?图片来源:Aatish Bhatia 图片来源:Aatish Bhatia
图片来源:Aatish Bhatia 图片来源:Aatish Bhatia
图片来源:Aatish Bhatia 图片来源:Aatish Bhatia
图片来源:Aatish Bhatia 桔子皮不可能压成完整圆——因为球面和平面高斯曲率不同(而且桔子皮也没有什么延展性)。图片来源:Aatish Bhatia
桔子皮不可能压成完整圆——因为球面和平面高斯曲率不同(而且桔子皮也没有什么延展性)。图片来源:Aatish Bhatia 每个红色圆圈的实际面积是相等的,但在地图上看起来就有很大的差异。图片来源:Stefan Kühn (左), Eric Gaba (右) / Wikimedia
每个红色圆圈的实际面积是相等的,但在地图上看起来就有很大的差异。图片来源:Stefan Kühn (左), Eric Gaba (右) / Wikimedia 没想到几何学也能这么美味吧。图片来源:Aatish Bhatia
没想到几何学也能这么美味吧。图片来源:Aatish Bhatia 弯曲的草叶。图片来源:Dudley Carr / Flickr
弯曲的草叶。图片来源:Dudley Carr / Flickr 西班牙扎祖拉体育场。图片来源:Ximo Michavila
西班牙扎祖拉体育场。图片来源:Ximo Michavila 纸板箱里隐藏的秘密。图片来源:Craig Sunter / Flickr
纸板箱里隐藏的秘密。图片来源:Craig Sunter / Flickr 很多人小时候玩过的把戏:把一张纸折叠几次就能承载很大的重量,但它背后的数学可能你就想不到了。图片来源:Aatish Bhatia
很多人小时候玩过的把戏:把一张纸折叠几次就能承载很大的重量,但它背后的数学可能你就想不到了。图片来源:Aatish Bhatia 请务必在家中尝试一下——好吧,为了安全,别在电脑前尝试。图片来源:Aatish Bhatia
请务必在家中尝试一下——好吧,为了安全,别在电脑前尝试。图片来源:Aatish Bhatia 图片来源:Owen Cliffe / Wikimedia
图片来源:Owen Cliffe / Wikimedia 图片来源:Aatish Bhatia
图片来源:Aatish Bhatia 图片来源:Ciudad de las Artes y las Ciencias / Flickr
图片来源:Ciudad de las Artes y las Ciencias / Flickr
No comments:
Post a Comment