| |
| 6. 推廣到三維空間:Gauss 定理與 Stokes 定理 |
抓住了 Green 公式的形式與內涵,要推廣到三維空間就不難了。首先令
表示空間中的一個向量場 (Vector field),即定義在空間中某領域的一個向量值函數。
- 定義:
分別叫做向量場 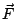 的散度與旋度。 的散度與旋度。
其次我們注意到,平面領域 Ω 可以有兩個方向的推廣:一個是空間中的可定向 (Orientable) 曲面 S(Möbius帶子就不是可定向曲面),參見圖16;另一個是空間中的一塊立體領域 V,參見圖17。
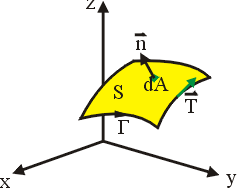
圖16 |
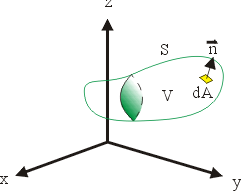
圖17 |
在(19)式中,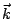 是 Ω 的向外單位法向量;當 Ω 改為空間曲面 S 時, 是 Ω 的向外單位法向量;當 Ω 改為空間曲面 S 時,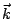 就應該改為 S 的向外單位向量 就應該改為 S 的向外單位向量 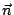 。 我們可以證明 。 我們可以證明 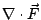 與 與 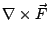 跟二維的情形有類似的解釋。 跟二維的情形有類似的解釋。 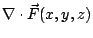 表示單位時間單位體積流體在點 表示單位時間單位體積流體在點 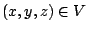 的流出通量, 的流出通量, 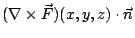 表示單位時間單位體積流體在點 表示單位時間單位體積流體在點 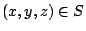 的循環量。從而(19)與(20)兩式就推廣為: 的循環量。從而(19)與(20)兩式就推廣為:
- 定理4: (Gauss 定理,又叫做散度定理,1839年)
- 設向量場
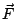 的分量 P,Q,R 及其一階偏導函數皆為連續函數,則 的分量 P,Q,R 及其一階偏導函數皆為連續函數,則
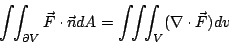 | (31) |
其中 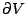 為圍成 V 之封閉曲面,dV 表示無窮小的體積元。 為圍成 V 之封閉曲面,dV 表示無窮小的體積元。
- 定理5: (Stokes 定理,又叫做旋度定理,1854年)
- 在與定理4相同的假設下,我們有
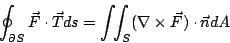 | (32) |
參見圖16。
在上述中,(31)式與(32)式分別將曲面積分與三重積分,線積分與曲面積分連結起來。若採用直角坐標系來表達,它們分別就是
以及
這一切可以再推廣到 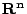 的可定向 k 維可微分子流形 的可定向 k 維可微分子流形 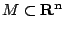 ,用微分式的積分與外微分理論,統合成為廣義的 Stokes 定理: ,用微分式的積分與外微分理論,統合成為廣義的 Stokes 定理:
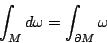 | (34) |
其中 ω 為 k-1 型微分式。這是微積分學根本定理最本質的形式。
学习外微分形式的一些感受
PB07210141 焦凡书
外微分形式把Stokes,Gauss公式联系起来,而且推广到高维空间。初学时觉得很“神奇”,查阅了一些书籍后才知道Poincare’指出多重积分的体积元素应有一个正负定向导致了外微分的出现。而外微分的出现可以说标志着微积分从古典走向现代。在物理,力学,偏微分方程,微分几何中,外微分发挥了巨大的作用。外微分有其更本质的含义,下面是我的一些总结和感受。
如果我们研究曲面(双侧曲面)的方向性,那么:在双侧曲面上任意取定一点M,并在M处选定一个单位法向量n(M),对于曲面S上任意一点M’,在S上做一条连接M,M’的曲线,由n(M’)沿曲线连续变化的原则,就可以唯一的确定M’处的单位法向量n(M’),从而就完全确定了双侧曲面的一个侧。曲面S在M处的单位法向量有且仅有两个,它们是互为相反方向的单位向量,这两个向量正好确定了曲面的两个定侧。
在双侧曲面内令:x=x(u,v) y=y(u.,v)
则面积元素dA=dxdy=|  |dudv=|  |dudv=(  )dudv
若将x,y 对换dA=dydx=|  |dudv=|  |dudv=(  )dudv
可得dxdy=-dydx
dxdx=0
我们把满足上述关系即:两个相同微分乘积为零,不同微分乘积变换顺序时变号的微分之间的乘积称为微分外积,用 表示。由微分的外乘积乘上函数组成的微分形式称为外微分形式。若 表示。由微分的外乘积乘上函数组成的微分形式称为外微分形式。若P,Q,R,H 是x,y,z 的函数,则Pdx+Qdy+Rdz 为一次外微分形式。Pdy  dz+Qdz  dx+Rdx  dy 为二次外微分形式,Hdx  dy  dz 为三次外微分形式。
可以证得(1 )Newton-Leibniz 公式用外微分表示 =f(b)-f(a)= 
(2 )Green 公式用外微分表示 Pdx+Qdy,  =  ,
(3 )Gauss 公式用外微分表示 Pdy  dz+Qdz  dx+Rdx  dy,  Pdy  dz+Qdz  dx+Rdx  dy=  dx  dy  dz, 
(4 )Stokes 公式用外微分表示 Pdx+Qdy+Rdz,  ,
而数量场的梯度,向量场的散度,旋度分别与之对应。因此他们的关系可以表示为
|
外微分形式的次数
|
空间
|
公式
|
对应的度
|
|
0
|
直线段
|
Newton-Leibniz
|
梯度
|
|
1
|
平面区域
|
Green
|
旋度
|
|
1
|
空间曲面
|
Stokes
|
旋度
|
|
2
|
空间区域
|
Gauss
|
散度
|
由此得出公式的一般形式:
G 是d  的积分区域, 的积分区域, G 表示G 的边界。
Stokes 公式揭示了微分与积分在空间上的关系。若令 , ,d 为算子,则它们对偶.
所以说Stokes公式是微积分中最本质的,由它引出了微分几何,广义相对论的很多内容,我的知识有限,希望以后有能力了解更多。
参考书目:《高等数学导论》
《微积分五讲》龚升
|
No comments:
Post a Comment