活能量很小,发生迁移的几率就很高,体系流变的
很快(如一般液体中的流变)。在外力或者温度作用
下,粒子的能量提高,等价于降低势垒(如图195 所
示),导致流变发生。非晶态是从液态凝固得到的,其
弛豫时间从液态和过冷液态的10¡14»10¡1 s 到非晶
态的> 102 » 107 s,有约12»14 个数量级的巨大时
间尺度差异。这种流变时间尺度的差异主要是其能垒
控制的。所以要研究非晶或者液体中的流变,关键是
要澄清控制流变势垒的物理因素是什么。
b. 非晶及液体和时间的关系
固体和液体的区别可以用一个无量纲数D,
即Deborah 数来表征。这个数是以圣经中的先
知Deborah 的名字命名的,因为他曾说过“群山在
上帝面前流动”[360]。Deborah 数D 定义为:
D = ¿ =t0 (76)
这里¿ 是弛豫时间, t0 是观察时间。如果你的观察时
间足够长,或者被观察的体系弛豫时间非常小,那么
你就会看到这个物体是在流动。相反,如果一个体系
的tr 远大于你的观察时间(人类的观察时间约分钟
量级),你就感觉不到该物体的流动,这个体系就是固
体。所以一个体系是非晶或是液体是相对的,决定于
观察时间。图162 表明玻璃转变和观察时间tr 相关,
就是因为液体和固体的定义是相对的,决定于我们的
观察时间尺度。
弹性模型就是基于这样的假设[29]:在足够短的
时间尺度或者高频条件下粘滞液体可以被看成是“流
动的固体”,或者说任何粘滞液体只要在足够快的
时间尺度去探测就会有类似固体的特征。即:粘滞
液体¼ 流动的固体[29]。这些液体的弹性可以用瞬
态模量G1,E1 和K1 来表征。现有所有的弹
性模型都基于这样的思想:非晶固体和非晶形成液
体之间的差别在于它他们承载切向应力的能力,体
系粘滞系数的急剧增加是由于液体中局域弛豫行为
的弹性相互作用的增强,即流动激活能主要由其体
系瞬态模量决定的[29]。这一思想最早是由Tobol-
sky,Powell 和Eyring 提出的[361;362]。
c. 非晶及液体流变的激活能
不同的物质的流动规律虽然不同,但其共同点就
是流动需要能量来克服流动势垒,即固体或液体中的
粒子或原子需要特定的能量才能摆脱其邻居的束缚发
生流变,Dyre 认为粘稠液体或者非晶中原子的流动
是“推挤”其它原子的迁移或逃逸的过程[29]。这个逃
逸过程需要的能量即激活能。在理解非晶“流动”、形
成、晶化等现象和问题时,激活能的概念非常重要。
激活能的概念是Arrhenius 最先在1889 提出的。
Arrhenius 关系在非晶研究中也非常重要,广泛使用。
非晶的很多热力学、动力学规律都符合Arrhenius 关
系。过冷液体的性质,玻璃转变以及其它研究和Ar-
rhenius 数学公式以及激活能有密切关系,因此有必要
介绍一下Arrhenius 及Arrhenius 公式的内涵。
Arrhenius 方程是瑞典物理、化学家阿瑞纽
斯(Arrhenius S. A. 1859-1927, 曾获1903 年诺贝尔化
学奖)1889 年提出的(图196是Arrhenius S. A. 的照
片)。Arrhenius 是在研究化学反应速率与温度关系时
发现化学反应速率与温度呈指数关系即Arrhenius 反
应速率定律,并提出激活能(最初被称作活化能)的概
念[363]。Arrhenius 反应速率定律为:简单化学反应的
速率以exp(¡E=kBT)的形式依赖于温度,其中E 是
化学反应中不依赖于温度的特征常数|激活能。Ar-
rhenius 是在他的博士论文《电解质的导电性研究》中
提出了反应速率与温度的关系,提出活化能的概念及
Deborah number
From Wikipedia, the free encyclopedia
The Deborah number (De) is a dimensionless number, often used in rheology to characterize the fluidity of materials under specific flow conditions. It is based on the premise that given enough time even a solid-like material will flow. The flow characteristics are not inherent properties of the material alone, but a relative property which depends on two fundamentally different characteristic times.
Formally, the Deborah number is defined as the ratio of the relaxation time characterizing the time it takes for a material to adjust to applied stresses or deformations, and the characteristic time scale of an experiment (or a computer simulation) probing the response of the material. It incorporates both the elasticity and viscosity of the material. At lower Deborah numbers, the material behaves in a more fluidlike manner, with an associated Newtonian viscous flow. At higher Deborah numbers, the material behavior enters the non-Newtonian regime, increasingly dominated by elasticity and demonstrating solidlike behavior.[1][2]
The equation is thus:
History
It was originally proposed by Markus Reiner, a professor at Technion in Israel, inspired by a verse in the Bible, stating "The mountains flowed before the Lord" in a song by prophetess Deborah (Judges 5:5).
Time-Temperature Superposition
The Deborah Number is particularly useful in conceptualizing the Time–temperature superposition principle. Time-Temperature superposition has to do with altering experimental time scales using reference temperatures to extrapolate on the temperature-dependent mechanical properties of polymers. A material at low temperature with a long experimental or relaxation time behaves like the same material at high temperature and short experimental or relaxation time if the Deborah number remains the same. This can be particularly useful when working with materials which relax on a long time scale under a certain temperature. The practical application of this idea arises in the Williams–Landel–Ferry equation. Time-temperature superposition avoids the inefficiency of measuring a polymer’s behavior over long periods of time at a specified temperature by utilizing the Deborah Number.[3]
底波拉数[编辑]
Formally, the Deborah number is defined as the ratio of the relaxation time characterizing the time it takes for a material to adjust to applied stresses or deformations, and the characteristic time scale of an experiment (or a computer simulation) probing the response of the material. It incorporates both the elasticity and viscosity of the material. At lower Deborah numbers, the material behaves in a more fluidlike manner, with an associated Newtonian viscous flow. At higher Deborah numbers, the material behavior enters the non-Newtonian regime, increasingly dominated by elasticity and demonstrating solidlike behavior.[1][2]
The equation is thus:
History
It was originally proposed by Markus Reiner, a professor at Technion in Israel, inspired by a verse in the Bible, stating "The mountains flowed before the Lord" in a song by prophetess Deborah (Judges 5:5).
Time-Temperature Superposition
The Deborah Number is particularly useful in conceptualizing the Time–temperature superposition principle. Time-Temperature superposition has to do with altering experimental time scales using reference temperatures to extrapolate on the temperature-dependent mechanical properties of polymers. A material at low temperature with a long experimental or relaxation time behaves like the same material at high temperature and short experimental or relaxation time if the Deborah number remains the same. This can be particularly useful when working with materials which relax on a long time scale under a certain temperature. The practical application of this idea arises in the Williams–Landel–Ferry equation. Time-temperature superposition avoids the inefficiency of measuring a polymer’s behavior over long periods of time at a specified temperature by utilizing the Deborah Number.[3]
底波拉数[编辑]
维基百科,自由的百科全书
底波拉數是流變學中的一個无量纲量,用來描述材料在特定條件下的流動性。底波拉數最早是由以色列理工学院的教授馬庫斯·萊納所提出,其名稱來自於聖經《士師記》5:5中,士師底波拉歌中的一句:
底波拉數是假設在時間足夠的條件下,即使是最堅硬的物體(例如山)也會流動。因此流動特性不是一個材料本身的固有属性,而是一種相對属性,此相對属性和二個有本質上完全不同的特徵時間有關。
底波拉數定義為馳豫時間及觀測時間尺度的比值。馳豫時間表示一材料反應施力或形變時所需要的時間,觀測時間尺度是指探索材料反應的實驗(或電腦模擬)的時間尺度。底波拉數中整合了材料的彈性及粘滯度。若底波拉數越小,材料特性越接近流體,其運動越接近牛頓粘性流。若底波拉數越大,材料特性主要以彈性為主,底波拉數非常高時,材料特性接近固體[1] [2]。
其方程式為:
“
山見耶和華的面就震動。
”
底波拉數定義為馳豫時間及觀測時間尺度的比值。馳豫時間表示一材料反應施力或形變時所需要的時間,觀測時間尺度是指探索材料反應的實驗(或電腦模擬)的時間尺度。底波拉數中整合了材料的彈性及粘滯度。若底波拉數越小,材料特性越接近流體,其運動越接近牛頓粘性流。若底波拉數越大,材料特性主要以彈性為主,底波拉數非常高時,材料特性接近固體[1] [2]。
其方程式為:
- tc是指應力的馳豫時間(有時稱為馬克士威馳豫時間)
- tp是指觀測的時間尺度
參考資料[编辑]
- ^ Reiner, M., The Deborah Number, Physics Today. 1964, 17 (1): 62, doi:10.1063/1.3051374
- ^ The Deborah Number
- J.S. Vrentas, C.M. Jarzebski, J.L. Dudda (1975) "A Deborah number for diffusion in polymer-solvent systems", AIChE Journal 21(5):894–901, weblink to Wiley Online Library.
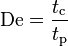
No comments:
Post a Comment