（分享）切空间的引入
漫谈几何量子化（四）表象
在场论中，经典相空间一般都是无穷维空间。无穷维缺少有限维的一个重要性质，即平移旋转不变的 Lebesgue 测度的存在性
漫谈几何量子化（七）流形
经典相空间一般都是辛空间，从历史角度来说就是可以写下 Hamilton 运动方程的空间。数学上把量子化总结为从一个辛空间出发构造 Hilbert 空间及其上一系列满足 Heisenberg 交换关系的算子的问题。谐振子的例子里，这个辛空间本质上只是一个向量空间，物理学家往往称这种空间为“拓扑平凡的”。数学上非常感兴趣的是，给一个“拓扑非平凡”的辛空间，量子化到底是什么意思。
一类拓扑非平凡的空间都落在一个比较好的范畴中，它们在数学上就叫“流形”。一个 n 维“流形”是一个拓扑空间，它的每个局部在拓扑上都等价于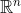
的开集，就是说，局部上每个点对应到 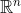的一个点，有一组坐标，这就是局部坐标系。两个局部重叠的地方，就有两个局部坐标系，它们相差一个坐标变换。由以上定义，这些坐标变换自然是拓扑等价（即双方连续的一一对应）。如果其中某些坐标变换还是无穷次可微的，而且它们涉及到的局部可以合起来覆盖整个流形，那么这个流形就是“光滑”的。把所有互为光滑变换的局部坐标系都收集起来，它们叫做这个光滑流形的“容许坐标系”。
在光滑流形上，可以谈论“光滑”函数。一个函数如果在一个容许坐标系下是光滑的，那么在另一个重叠的容许坐标系下也光滑，因为坐标变换是光滑的。通常这么叙述这种好处：光滑性不依赖于局部坐标选取。在流形上，与局部坐标选取无关的“概念”，“性质”，和与局部坐标变换相容的“ 量”，才是有几何意义的。这一点，微分几何的创始人 Gauss, Riemann 应该都心里有数。Einstein 在他的物理学里也强调了这一点。
在流形上没有线性结构，不能把两个点加在一起，也不能连接两个点成为一个“向量”。不过在每一点的局部，就好像在欧氏空间一样，可以在这一点对函数“求方向导数”，这种运算是局部函数空间上的线性算子。以它们为模型的整体对象叫做在该点的“切向量”。在局部上还有一个有趣的东西就是函数在一点的“微分”，
以它为模型的整体对象叫做一个“余切向量”（或者仍然叫做微分）。然后顾名思义，一个“光滑切向量场”就是在每一点有一个切向量，以光滑方式依赖于基点。对偶的概念是“微分 1－形式”，即，光滑余切向量场。在局部坐标系下，切向量场和微分 1-形式通常写成
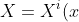\frac{\partial}{\partial x^i},\qquad \xi = \xi_i(x) \,dx^i "X=X^i(x)\frac{\partial}{\partial x^i},\qquad \xi = \xi_i(x) \,dx^i")
这里用了 Einstein 求和约定。系数都是局部坐标系里的光滑函数（但不是整体的光滑函数，将随坐标变换而变）。
在每一点上，由方向导数和微分组成的多重线性对象，以整体方式定义以后，叫“张量”。张量场跟前面类似。搞数学的喜欢用整体记号，就像上面那个式子一样，把分量和基写在一起，变换局部坐标的时候，基底和分量同时变，而它们的组合不变，从而左边的字母代表一个不依赖于局部坐标系的量；搞物理的喜欢只写出分量而省略基底，这样的记号明显依赖于局部坐标系
漫谈几何量子化（七）流形
经典相空间一般都是辛空间，从历史角度来说就是可以写下 Hamilton 运动方程的空间。数学上把量子化总结为从一个辛空间出发构造 Hilbert 空间及其上一系列满足 Heisenberg 交换关系的算子的问题。谐振子的例子里，这个辛空间本质上只是一个向量空间，物理学家往往称这种空间为“拓扑平凡的”。数学上非常感兴趣的是，给一个“拓扑非平凡”的辛空间，量子化到底是什么意思。
一类拓扑非平凡的空间都落在一个比较好的范畴中，它们在数学上就叫“流形”。一个 n 维“流形”是一个拓扑空间，它的每个局部在拓扑上都等价于
在光滑流形上，可以谈论“光滑”函数。一个函数如果在一个容许坐标系下是光滑的，那么在另一个重叠的容许坐标系下也光滑，因为坐标变换是光滑的。通常这么叙述这种好处：光滑性不依赖于局部坐标选取。在流形上，与局部坐标选取无关的“概念”，“性质”，和与局部坐标变换相容的“ 量”，才是有几何意义的。这一点，微分几何的创始人 Gauss, Riemann 应该都心里有数。Einstein 在他的物理学里也强调了这一点。
在流形上没有线性结构，不能把两个点加在一起，也不能连接两个点成为一个“向量”。不过在每一点的局部，就好像在欧氏空间一样，可以在这一点对函数“求方向导数”，这种运算是局部函数空间上的线性算子。以它们为模型的整体对象叫做在该点的“切向量”。在局部上还有一个有趣的东西就是函数在一点的“微分”，
以它为模型的整体对象叫做一个“余切向量”（或者仍然叫做微分）。然后顾名思义，一个“光滑切向量场”就是在每一点有一个切向量，以光滑方式依赖于基点。对偶的概念是“微分 1－形式”，即，光滑余切向量场。在局部坐标系下，切向量场和微分 1-形式通常写成
这里用了 Einstein 求和约定。系数都是局部坐标系里的光滑函数（但不是整体的光滑函数，将随坐标变换而变）。
在每一点上，由方向导数和微分组成的多重线性对象，以整体方式定义以后，叫“张量”。张量场跟前面类似。搞数学的喜欢用整体记号，就像上面那个式子一样，把分量和基写在一起，变换局部坐标的时候，基底和分量同时变，而它们的组合不变，从而左边的字母代表一个不依赖于局部坐标系的量；搞物理的喜欢只写出分量而省略基底，这样的记号明显依赖于局部坐标系
看不下去。。。符号的悲剧。。。- 巫毒璨
- SUSY9
帖子貌似要沉了。我这里补充几句解释一下几个概念。
先说等价关系，等价关系就是集上定义的具有自反性，对称性，传递性这三中性质的集的一个分类（或者说剖分）。举个例子比如今天去班里上课的学生，他们可能各有不同，但你总能找到一个关系把他们分类。把他们按衣服颜色分类，蓝色的一类，红色的一类等等。很明显衣服的a同学与自身衣服颜色相同，具有自反性。同学b和同学c颜色相同，则同学c与同学b颜色相同，具有对称性。a与b颜色相同，b与c相同，则a与c相同，具有传递性。再定义一个关系如血缘关系，很明显这不是一个等价关系，比如你和你的父母有共同祖先，但这个关系不能由你传递给你的父母，你的父母本来祖先就不同。等价关系将**分成了两两不相交的**，按等价关系两**要么相等要么不相交，这些**的并等于原**。商集和就是某个等价关系的全体，可以选取等价类的代表元素来表示他，当然附加某些结构，就成为商环，商群，商空间等等。
先说等价关系，等价关系就是集上定义的具有自反性，对称性，传递性这三中性质的集的一个分类（或者说剖分）。举个例子比如今天去班里上课的学生，他们可能各有不同，但你总能找到一个关系把他们分类。把他们按衣服颜色分类，蓝色的一类，红色的一类等等。很明显衣服的a同学与自身衣服颜色相同，具有自反性。同学b和同学c颜色相同，则同学c与同学b颜色相同，具有对称性。a与b颜色相同，b与c相同，则a与c相同，具有传递性。再定义一个关系如血缘关系，很明显这不是一个等价关系，比如你和你的父母有共同祖先，但这个关系不能由你传递给你的父母，你的父母本来祖先就不同。等价关系将**分成了两两不相交的**，按等价关系两**要么相等要么不相交，这些**的并等于原**。商集和就是某个等价关系的全体，可以选取等价类的代表元素来表示他，当然附加某些结构，就成为商环，商群，商空间等等。
- 巫毒璨
- SUSY9
这个p点开领域的光滑函数的全体无法构成线性空间，因为f（p）＝g（p）＝0的函数无限多，不唯一，不满足构成线性空间的条件，所以按上面的等价关系形成的商空间函数牙就是选取了值为0的等价类中的一个函数作为唯一的零元。
Hp是Fp的字空间，Fp中元素v1－v2如果属于Hp，就令v1＝v2，这是也是一个等价关系，确定了Fp的一个分类。这个关系下商空间Fp/HP仍是线性空间。
Hp是Fp的字空间，Fp中元素v1－v2如果属于Hp，就令v1＝v2，这是也是一个等价关系，确定了Fp的一个分类。这个关系下商空间Fp/HP仍是线性空间。
- 共有1页
- 回复贴: 34
- 巫毒璨
- SUSY9
帖子貌似要沉了。我这里补充几句解释一下几个概念。
先说等价关系，等价关系就是集上定义的具有自反性，对称性，传递性这三中性质的集的一个分类（或者说剖分）。举个例子比如今天去班里上课的学生，他们可能各有不同，但你总能找到一个关系把他们分类。把他们按衣服颜色分类，蓝色的一类，红色的一类等等。很明显衣服的a同学与自身衣服颜色相同，具有自反性。同学b和同学c颜色相同，则同学c与同学b颜色相同，具有对称性。a与b颜色相同，b与c相同，则a与c相同，具有传递性。再定义一个关系如血缘关系，很明显这不是一个等价关系，比如你和你的父母有共同祖先，但这个关系不能由你传递给你的父母，你的父母本来祖先就不同。等价关系将**分成了两两不相交的**，按等价关系两**要么相等要么不相交，这些**的并等于原**。商集和就是某个等价关系的全体，可以选取等价类的代表元素来表示他，当然附加某些结构，就成为商环，商群，商空间等等。
先说等价关系，等价关系就是集上定义的具有自反性，对称性，传递性这三中性质的集的一个分类（或者说剖分）。举个例子比如今天去班里上课的学生，他们可能各有不同，但你总能找到一个关系把他们分类。把他们按衣服颜色分类，蓝色的一类，红色的一类等等。很明显衣服的a同学与自身衣服颜色相同，具有自反性。同学b和同学c颜色相同，则同学c与同学b颜色相同，具有对称性。a与b颜色相同，b与c相同，则a与c相同，具有传递性。再定义一个关系如血缘关系，很明显这不是一个等价关系，比如你和你的父母有共同祖先，但这个关系不能由你传递给你的父母，你的父母本来祖先就不同。等价关系将**分成了两两不相交的**，按等价关系两**要么相等要么不相交，这些**的并等于原**。商集和就是某个等价关系的全体，可以选取等价类的代表元素来表示他，当然附加某些结构，就成为商环，商群，商空间等等。
- 巫毒璨
- SUSY9
这个p点开领域的光滑函数的全体无法构成线性空间，因为f（p）＝g（p）＝0的函数无限多，不唯一，不满足构成线性空间的条件，所以按上面的等价关系形成的商空间函数牙就是选取了值为0的等价类中的一个函数作为唯一的零元。
Hp是Fp的字空间，Fp中元素v1－v2如果属于Hp，就令v1＝v2，这是也是一个等价关系，确定了Fp的一个分类。这个关系下商空间Fp/HP仍是线性空间。
Hp是Fp的字空间，Fp中元素v1－v2如果属于Hp，就令v1＝v2，这是也是一个等价关系，确定了Fp的一个分类。这个关系下商空间Fp/HP仍是线性空间。
- 巫毒璨
- SUSY9
这里的一个写在两个函数中间的类似句号的符号，是函数复合符号满足结合律和分配律，但不满**换律。f。g（）意思就是f（g（t）），f。g＝f。h。h^（－1）。g，如果h。h^（－1）是连续函数。
- 巫毒璨
- SUSY9
式2.19用到了正交曲线坐标系
- wolfking97: “正交曲线坐标系”的说法有点意思，不过也容易误导。这里其实是取了坐标函数u^i给出的由u^i=u^i(p)确定的超曲面经过p点的法向曲线（拉回到欧氏空间就是我们平常xyz坐标下的坐标轴）。这个时候应该还没有度量吧，所以不会有内积和正交的概念。
2012-12-20 06:57回复
- 巫毒璨
- SUSY9
当给出y的一个等价关系y～y'时，Γp由此也形成了一个线性空间，这时〈，〉很明显就是一个内积。后面的共轭变换和量子力学算符的共轭转置是一样的，这里是线性空间间的线性变换。
- wolfking97: 通常我们把这个叫做配对，不叫内积。内积是同一个线性空间中两个矢量的一种乘积，上面的<,>是对偶空间中的元素（也叫线性泛函）在空间上的作用。
2012-12-20 07:16回复
-
- 叶世杰2
- Higgs7
一般定义切空间都是用我们比较熟悉的坐标系定义的，然后再证明切空间不依赖坐标系的选择。陈书这里直接从流形上的标量函数这个无关坐标系的概念出发，得到余切空间，切空间，好处是直接说明这些概念是流形内隐的，具有所谓数学的纯粹性。不好的是对非数学专业的或初学人士显得抽象，因为要用到**等价类，商**等这样一些抽象代数的概念。
- 共有1页
- 回复贴: 34
舞动
诸侯上将
热战绿色版
书剑江湖
No comments:
Post a Comment