"广义相对论处处无源", time like in space 空间, brain; 类空, different matter/空间
penrose 674
加加速度它的物理意義是什麼？是位置向量r的三次微分？
0Comment count
|
1View count
|
8/15/14
| |||||
0Comment count
|
1View count
|
8/15/14
| |||||
0Comment count
|
1View count
|
8/15/14
| |||||
0Comment count
|
1View count
|
8/15/14
| |||||
泰勒展開式多极子展开法初级源源多个点源叠加 「笛卡兒多極展開」（Cartesian multipole expansion）；另一種 .... 這電偶極矩與原點位置無關，與兩個點電荷之間的相對位置有關
在狭义相对论中，加速度的变换公式冗长而复杂，各分量的公式也极不相似。再加上如果要考虑到力，虽然
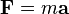 仍然成立，但质量也会变得随参考系的不同而不同。以上原因导致加速度在牛顿力学中那种因为简洁而具有的优越性，在狭义相对论中不复存在，必須使用更有功能的數學工具，即張量分析
牛顿认为运动的物体有不变的惯性质量，因此他能够不考虑物体的长、宽、高而把物体看成是质点具有一定质量的，不计尺寸大小的粒子
http://shc2000.sjtu.edu.cn/phy/phy1.htm
对宇宙来说，所谓统一时间（把作惯性运动的物体的坐标认为是时间的线性函数）只是对某个确定的范围内可以使用的近似的概念 在廿世纪物理学中基本理论的扩展，即相对论、量子力学、相对论量子力学和量子电动力学对古典物理学全部最普遍最基本的概念进行一系列的修正。相对论突破了时间和空间的独立性和质量的不变性。接着在1916年又突破了在引力场中的惯性运动和加速运动的区别。狭义相对论把古典物理学中具有根本意义的假定之一降低到仅仅是近似的等级。在古典物理学中力学的惯性系是等价的，但是还有一个与其相对立的，有特权的，普遍的宇宙以太系统。在1905年，事情已经清楚了，相对于以太运动是一个毫无内容的概念。空间和时间的间隔将随着运动系统而改变，当从一个惯性系过渡到另一个惯性系时，光速将保持同样的数值，因之时间长短的本身只是对于给定的坐标系统才有确定的意义。只要问题不容许无穷大光速的概念，对不同的系统来谈论统一的时间就没有任何意义了。对宇宙来说，所谓统一时间（把作惯性运动的物体的坐标认为是时间的线性函数）只是对某个确定的范围内可以使用的近似的概念。在由狭义相对论所产生的变革的深处，古典的世界图景的根基被保留下来。这个根基就是绝对自身同一的，分立存在的彼此运动的物体的表象。分立存在的物体运动于连续的空间中，其相互距离是连续的时间的函数。这种传统的把现实分割为时空连续统和在它里面运动的分立存在的物体作法，当从宇宙图景中消除了连续的充满空间的以太，当物体相对于被静止以太所充满的空间的运动概念失去意义的时候仍旧被保持下来。广义相对论带来了更为根本的变化。在把引力场比拟为弯曲的时空之后，广义相对论就把引力场中的运动和惯性运动之对比完成了。如果说古典力学认为在没有力场作用时，物体将沿着直的世界线运动（即欧氏空间的最短线），那么广义相对论则断言，在引力场中，物体将沿着最短线（测地线）运动。总之，引力场只意味着它超出了四维时空连续统中欧氏几何的关系，并使这一连续统弯曲。这时就好象把场以确定的依赖于质量积累的几何特性溶合到时空之中。 |
转载▼转自 http://www.fxkz.net/viewthread.php?tid=2380&highlight=
中文完全版。翻译虽做过校对，不严谨甚至错误之处仍属难免，故敬请诸位高手跟贴指正。转载请注明来自新繁星客栈。(承星空兄建议，将此贴重新发表一次，一鱼两吃，不好意思。请版主将前贴<< 虚粒子图像如何解释吸引力或排斥力 >>撤销。)
英文原贴连接:
To and for my angel.
内容：
1. 什么是虚粒子？
2. 虚粒子如何解释吸引力？
3. 虚粒子违逆能量守恒吗？
4. 虚粒子以超光速传播？虚粒子与相对论或因果律相矛盾吗？
5. 我听一些物理学家说“重力的量子”叫做重力子啥的，广义相对论不是说重力根本不是力吗？
1. 什么是虚粒子？
量子力学最初的进展中的一步是马克斯．普朗克的一个观点：即谐振子（经典地看，谐振子就是类似于系于理想弹簧一端来回晃动的物体）的能量不能随便取值，其能量只可能是等间隔能阶对应的分立值。
带有波动的电磁场以同样的方式晃动。将量子力学用于这种振子时可以发现，它也必拥有分立、间隔均匀的能阶。我们通常把这些能阶对应成不同的光子数目。一个振动模式的能量越高，它拥有的光子数目就越大。依这个理解方式，一个电磁波的行为就犹如它是由一些粒子构成的。电磁场就成为量子场。
除振动以外，电磁场还另有作为。例如，电场在带电物体之间产生吸引或排斥力，力的大小与距离平方成反比。这样的力可以改变物体的动量。
这也能够用光子来理解吗？结果发现，在一定意义下，这是做得到的。我们可以说相互作用的粒子们“交换虚光子”，由虚光子来承载粒子之间所传递的动量。这里是交换一个虚光子的图画（费曼图）：
其中，左边和右边的线代表两个带电粒子，波浪线（由于ASCII码的限制而呈现间断）代表虚光子，它将动量由一个粒子传递给另一个粒子。发射虚光子的粒子失去动量p导致反冲，另一个粒子则得到这份动量。
这个解释看上去很精致。这里，力不是由于任何超距作用所致，而是由于虚粒子从一些东西蹦出然后撞到另一些东西上，敲打它们而使之运动。但这个图像是具有误导性的。虚粒子可不只是经典的弹丸。
2. 虚粒子图像如何解释吸引力或排斥力？
下面我们试图用虚粒子图像解释粒子之间的相互作用力，特别重要的是，虚粒子图像如何解释吸引力？
基于简单经典图像的虚粒子，一个最显而易见的毛病是其行为无法产生吸引力。试想，假如我抛给你一个球，反冲把我往后推，而你接到球时，你也是被推离我。这怎么会使我们互相吸引呢？
答案在于海森堡的不确定性原理中。
现在我们假设有一对粒子，其位置都很好地定域在空间某一很小范围，我们要来计算某一动量p在这对粒子之间转移的机率（幅度）。不确定性原理断言确定的动量必伴随位置的巨大不确定性。具动量p的一个虚粒子对应一个平面波，充满整个空间，根本没有确定的位置。动量指向何方没有关系，因为它仅决定波前的取向。既然对应虚粒子的波无处不在，故无论粒子位在何处，虚粒子总可以被一个粒子产生而被另一个粒子所吸收。如果被转移的动量之指向系从接收粒子到发射粒子，此一动量转移的效果为吸引力。在此你也可以见到虚粒子的“传播”可以是超光速的，甚至可以是不需要时间的。
要点是费曼图中那些线不能生硬地解释成经典粒子的路径。事实上，通常这种解释更不能用于我们当前的例子，盖因大多数费曼图中，入射粒子和出射粒子均非良好定域于空间，故皆应视为平面波。
藉助虚粒子传递动量而既可以导致排斥力也可以导致吸引力，是不确定性原理为之打开了可能性之门。但是你很自然地会追问，是什么导致同荷之间产生排斥而异荷之间产生吸引？难道虚光子知道它将撞到的粒子负载哪一种荷？
即算粒子物理学家使用量子电动力学（QED）的费曼图规则也不容易看清这一点，这是因为费曼图的通常理论表述方式是为了回答一个完全不同的问题而量身订造的：计算处在平面波状态的粒子从不同角度互相散射而到达新的平面波状态之机率。而这里，我们想弄清的是啥东西让一对相隔一定距离的粒子推搡拉扯，也就是要解释你在中学里可能做过的实验，其中你发现悬于丝线的铝箔带电球互相排斥。我们现在要用虚粒子来解释它。这做得到。
与一般的量子力学一样，在QED中，存在取复值的波函数，要对其取平方（模的平方）方可得到机率值。我们想要得到的是波函数以这样一种方式变化：同荷粒子对的波函数，平均而言，会互相排斥，而异荷粒子对的波函数，平均而言，会互相吸引。
为简单起见，假定载荷粒子之初始波函数为静止的高斯函数（波包），也就是通常的钟形实值函数，并假定它们都沿x轴排列。你可以将这些波函数想象成下面的样子：