[PDF]
Option pricing under stochastic volatility
www.economics.gu.se/.../1342760_mscthesisl--vg...
Gothenburg University
Loading...
by R Kjellin - 2006 - Cited by 4 - Related articles
Jan 25, 2006 - volatility and the stock price affects the behavior of option prices quite much. ..... Arithmetic Asian option The Asian options uses the mean level of the ...... a stochastic optimization algorithm - the so called simulated annealing.
www.economics.gu.se/.../1342760_mscthesisl--vg...
Gothenburg University
Loading...
by R Kjellin - 2006 - Cited by 4 - Related articles
Jan 25, 2006 - volatility and the stock price affects the behavior of option prices quite much. ..... Arithmetic Asian option The Asian options uses the mean level of the ...... a stochastic optimization algorithm - the so called simulated annealing.On pricing discrete barrier options using conditional ...
www.sciencedirect.com/science/.../S0895717707001963
ScienceDirect
Loading...
by G Ökten - 2008 - Cited by 8 - Related articles
Mathematical and Computer Modelling ... We use a simulated annealing algorithm to estimate the optimal parameters of exponential twisting in .... The crude Monte Carlo estimates I I by simulating N N stock price paths, averaging over the values ...... Pricing exotic options: Monotonicity in volatility and efficient simulation.
www.sciencedirect.com/science/.../S0895717707001963
ScienceDirect
Loading...
by G Ökten - 2008 - Cited by 8 - Related articles
Mathematical and Computer Modelling ... We use a simulated annealing algorithm to estimate the optimal parameters of exponential twisting in .... The crude Monte Carlo estimates I I by simulating N N stock price paths, averaging over the values ...... Pricing exotic options: Monotonicity in volatility and efficient simulation.蒙特卡洛模拟中,组态跃迁几率的两种表达式是怎么来的呢
川崎(Kawasaki)算法
建议你把Understanding Molecular Simulation里关于Monte Carlo的介绍(3.1节)仔细阅读一下,在3.1.2节中讲到了Detailed balance principle,detailed balance 无非就是
P_i * T(i->j) = P_j *T(j->i)
T(i->j) 和T(j->i)在这里就是transition probability,在正则系综中,P_i=exp(-E_i/kT),正如书中所说,在Monte Carlo模拟中,transition probability的选择可以有多种形式,只要它们满足由detailed balance principle所决定的比例关系(可能还有些额外要求,具体细节我不太了解)
T(i->j) /T(j->i)=P_j/P_i = exp(-(E_j - E_i)/kT),
那么你最后得到的概率分布就会收敛到玻尔兹曼分布。采用不同的transition probability会导致不同的收敛速度,这个就是个很技术的问题了。
所以你列出的两个transition probability都满足detailed balance principle的比例关系,所以都是可以的。
P_i * T(i->j) = P_j *T(j->i)
T(i->j) 和T(j->i)在这里就是transition probability,在正则系综中,P_i=exp(-E_i/kT),正如书中所说,在Monte Carlo模拟中,transition probability的选择可以有多种形式,只要它们满足由detailed balance principle所决定的比例关系(可能还有些额外要求,具体细节我不太了解)
T(i->j) /T(j->i)=P_j/P_i = exp(-(E_j - E_i)/kT),
那么你最后得到的概率分布就会收敛到玻尔兹曼分布。采用不同的transition probability会导致不同的收敛速度,这个就是个很技术的问题了。
所以你列出的两个transition probability都满足detailed balance principle的比例关系,所以都是可以的。
3楼: Originally posted by lsloneil at 2014-07-30 13:14:25
建议你把Understanding Molecular Simulation里关于Monte Carlo的介绍(3.1节)仔细阅读一下,在3.1.2节中讲到了Detailed balance principle,detailed balance 无非就是
P_i * T(i->j) = P_j *T(j->i)
T(i ...
灰常感谢你的详细回复,我稍微明白一些了建议你把Understanding Molecular Simulation里关于Monte Carlo的介绍(3.1节)仔细阅读一下,在3.1.2节中讲到了Detailed balance principle,detailed balance 无非就是
P_i * T(i->j) = P_j *T(j->i)
T(i ...
谢谢你提供细致平衡原理的参考出处,我没好好学过统计力学(汗颜。。。),搜了半天都没找到有用的资料
2楼: Originally posted by lei0736 at 2014-07-30 11:55:32
川崎(Kawasaki)算法
不好意思,我对这个算法不太熟悉,搜索了一下似乎不得要领,能请你稍微详细一些吗川崎(Kawasaki)算法
模拟退火算法编辑
本词条缺少信息栏,补充相关内容使词条更完整,还能快速升级,赶紧来编辑吧!
目录
1简介编辑
模拟退火算法(Simulated Annealing,SA)最早的思想是由N. Metropolis[1] 等人于1953年提出。1983 年,S. Kirkpatrick 等成功地将退火思想引入到组合优化领域。它是基于Monte-Carlo迭代求解策略的一种随机寻优算法,其出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。模拟退火算法从某一较高初温出发,伴随温度参数的不断下降,结合概率突跳特性在解空间中随机寻找目标函数的全局最优解,即在局部最优解能概率性地跳出并最终趋于全局最优。模拟退火算法是一种通用的优化算法,理论上算法具有概率的全局优化性能,目前已在工程中得到了广泛应用,诸如VLSI、生产调度、控制工程、机器学习、神经网络、信号处理等领域。
模拟退火算法是通过赋予搜索过程一种时变且最终趋于零的概率突跳性,从而可有效避免陷入局部极小并最终趋于全局最优的串行结构的优化算法。
2模拟退火算法的原理编辑
模拟退火算法来源于固体退火原理,将固体加温至充分高,再让其徐徐冷却,加温时,固体内部粒子随温升变为无序状,内能增大,而徐徐冷却时粒子渐趋有序,在每个温度都达到平衡态,最后在常温时达到基态,内能减为最小。根据Metropolis准则,粒子在温度T时趋于平衡的概率为e(-ΔE/(kT)),其中E为温度T时的内能,ΔE为其改变量,k为Boltzmann常数。用固体退火模拟组合优化问题,将内能E模拟为目标函数值f,温度T演化成控制参数t,即得到解组合优化问题的模拟退火算法:由初始解i和控制参数初值t开始,对当前解重复“产生新解→计算目标函数差→接受或舍弃”的迭代,并逐步衰减t值,算法终止时的当前解即为所得近似最优解,这是基于蒙特卡罗迭代求解法的一种启发式随机搜索过程。退火过程由冷却进度表(Cooling Schedule)控制,包括控制参数的初值t及其衰减因子Δt、每个t值时的迭代次数L和停止条件S。
模拟退火算法的模型
2模拟退火的基本思想:
(1) 初始化:初始温度T(充分大),初始解状态S(是算法迭代的起点),每个T值的迭代次数L
(2) 对k=1,……,L做第(3)至第6步:
(3) 产生新解S′
(4) 计算增量Δt′=C(S′)-C(S),其中C(S)为评价函数
(5) 若Δt′<0则接受S′作为新的当前解,否则以概率exp(-Δt′/T)接受S′作为新的当前解.
(6) 如果满足终止条件则输出当前解作为最优解,结束程序。
终止条件通常取为连续若干个新解都没有被接受时终止算法。
(7) T逐渐减少,且T->0,然后转第2步。
模拟退火算法的步骤
模拟退火算法新解的产生和接受可分为如下四个步骤:
第一步是由一个产生函数从当前解产生一个位于解空间的新解;为便于后续的计算和接受,减少算法耗时,通常选择由当前新解经过简单地变换即可产生新解的方法,如对构成新解的全部或部分元素进行置换、互换等,注意到产生新解的变换方法决定了当前新解的邻域结构,因而对冷却进度表的选取有一定的影响。
第三步是判断新解是否被接受,判断的依据是一个接受准则,最常用的接受准则是Metropolis准则: 若Δt′<0则接受S′作为新的当前解S,否则以概率exp(-Δt′/T)接受S′作为新的当前解S。
第四步是当新解被确定接受时,用新解代替当前解,这只需将当前解中对应于产生新解时的变换部分予以实现,同时修正目标函数值即可。此时,当前解实现了一次迭代。可在此基础上开始下一轮试验。而当新解被判定为舍弃时,则在原当前解的基础上继续下一轮试验。
模拟退火算法与初始值无关,算法求得的解与初始解状态S(是算法迭代的起点)无关;模拟退火算法具有渐近收敛性,已在理论上被证明是一种以概率l 收敛于全局最优解的全局优化算法;模拟退火算法具有并行性
細緻平衡 -正文
细致平衡,严格的热动平衡,即难以实现的微观可逆平衡状态。在高温气态等离子体中,原子、离子、电子均以很高的速度在运动着,彼此不断地互相碰撞
由於非彈性碰撞或吸收適當能量的光子,原子可以失去電子而成為離子(或離子失去電子而成為更高次電離離子),而另一些一次電離的離子由於碰撞或輻射出一定能量的光子而與電子複合為原子(高次電離離子則降低一次電離級);由於碰撞,原子(或離子)吸收一部分能量而被激發到較高能級,而另一些處於較高能級的原子(或離子)由於非彈性碰撞將其多餘能量轉移給與之相碰的粒子而降到較低的能級;一些原子(或離子)吸收了一定能量的光子而躍遷到較高能級,而另一些處於較高能級的原子(或離子)輻射出一定能量的光子而自發躍遷到較低能級。
當上述的高溫氣態等離子體處於熱動平衡狀態,而輻射場能量密度不是太小、氣體密度又是適中的時候,上述的正、反兩類過程就可能逐漸相對穩定,而達到一種嚴格的平衡狀態。也就是:①由於碰撞而從某一能級n上被(再次)電離的原子(或m次電離的離子)數目等於因碰撞而俘獲電子複合到同一能級的原子(或m次電離的離子)數目;②由於吸收適當能量的光子而從某一能級n上被(再次)電離的原子(或m次電離的離子)數目等於俘獲電子後放射出適當能量的光子而複合到同一能級的原子(或m次電離的離子)數目;③由於碰撞,原子(或離子)吸收了一定能量而從能級n被激發到更高能級n'上的數目等於因非彈性碰撞,原子(或離子)失去一定能量而從能級n'下落到能級n上的數目;④由於吸收一定能量的光子,原子(或離子)從能級n受迫躍遷到能級n'的數目等於輻射出一定能量的光子,而從能級n'自發躍遷到能級n的原子(或離子)數目。上述每一種正過程的數目都與它的逆過程的數目相等,這樣的一種平衡狀態便稱為細緻平衡。當高溫氣態等離子體一旦處於細緻平衡狀態時,它肯定就處於熱動平衡狀態,但是,處於熱動平衡狀態的高溫氣態等離子體卻未必處於細緻平衡狀態。
原子谱线[编辑]
物理学中,原子谱线是指原子内部电子跃迁形成的谱线,可分为两类:
跃迁中辐射或吸收的单个光子所携带的能量等于电子跃迁的两个能级之差,用普朗克公式即描述为能级差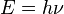 ,其中
,其中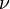 是光子的频率,而
是光子的频率,而 是普朗克常数。
是普朗克常数。
 来表示,其含义为单位时间单位体积单位立体角内辐射的能量。由此,
来表示,其含义为单位时间单位体积单位立体角内辐射的能量。由此, 则是在单位时间
则是在单位时间 内从单位体积
内从单位体积 中朝单位立体角
中朝单位立体角 方向上所辐射的能量。对原子发射谱线,发射系数为
方向上所辐射的能量。对原子发射谱线,发射系数为
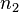 是处于发射状态的原子的数密度,而
是处于发射状态的原子的数密度,而 是自发辐射的爱因斯坦系数,这个系数对于任意两个特定的能级是定值。根据基尔霍夫热辐射定律,空间一定区域内的吸收特性是与它的发射特性密切相连的,因此我们也要同时考虑吸收谱线的吸收系数。吸收系数
是自发辐射的爱因斯坦系数,这个系数对于任意两个特定的能级是定值。根据基尔霍夫热辐射定律,空间一定区域内的吸收特性是与它的发射特性密切相连的,因此我们也要同时考虑吸收谱线的吸收系数。吸收系数 具有“1/长度”的量纲,从而
具有“1/长度”的量纲,从而 给出的是频率为一定的光在行走了距离
给出的是频率为一定的光在行走了距离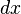 后被吸收的光强占总光强的比例。吸收系数的表达式为
后被吸收的光强占总光强的比例。吸收系数的表达式为
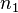 是处于吸收状态的原子的数密度,
是处于吸收状态的原子的数密度, 和
和 分别是爱因斯坦系数中的自发吸收和受激辐射的系数,它们对于任意两个特定的能级也是定值。
分别是爱因斯坦系数中的自发吸收和受激辐射的系数,它们对于任意两个特定的能级也是定值。
当系统处于局部的热平衡状态时,处于基态和激发态的原子各自的数密度满足麦克斯韦-玻尔兹曼分布;但对于非热平衡状态的情形(例如激光),原子的数密度分布计算会相当复杂。
上面列出的公式都假设了谱线对应的频率是单一的,即谱线是无形状的几何线,忽略了实际中不确定性原理及多普勒效应等因素造成的谱线展宽,实际的谱线是覆盖一段频率带宽的,具有一定的谱线形状。精确计算时要求这些公式乘以归一化的谱线形状,从而得到带有“1/频率”的量纲。
 ,它具有秒-1的量纲,表征的是在单位时间内电子从高能级
,它具有秒-1的量纲,表征的是在单位时间内电子从高能级 向低能级
向低能级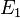 自发跃迁并释放出能量为
自发跃迁并释放出能量为 的光子的几率。由于能量-时间之间的不确定性关系,这一过程产生的光子实际占据了一段很窄的频率范围,即具有一定的线宽。如果假设处在两个能级的原子数密度分别为
的光子的几率。由于能量-时间之间的不确定性关系,这一过程产生的光子实际占据了一段很窄的频率范围,即具有一定的线宽。如果假设处在两个能级的原子数密度分别为 和
和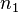 ,则自发辐射导致的低能级原子数密度
,则自发辐射导致的低能级原子数密度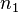 变化率为
变化率为
 ,它具有球面度·米2·赫兹·瓦特-1·秒-1(相当于球面度·米2·焦耳-1·秒-1)的量纲,表征的是在单位时间内辐射场的单位辐射亮度下电子从高能级
,它具有球面度·米2·赫兹·瓦特-1·秒-1(相当于球面度·米2·焦耳-1·秒-1)的量纲,表征的是在单位时间内辐射场的单位辐射亮度下电子从高能级 向低能级
向低能级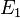 受激跃迁并释放出能量为
受激跃迁并释放出能量为 的光子的几率。如果假设处在两个能级的原子数密度分别为
的光子的几率。如果假设处在两个能级的原子数密度分别为 和
和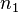 ,则受激辐射导致的低能级原子数密度
,则受激辐射导致的低能级原子数密度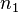 变化率为
变化率为
 是辐射场的辐射密度,它是受激频率
是辐射场的辐射密度,它是受激频率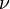 的函数(参见普朗克定律)。
的函数(参见普朗克定律)。
受激辐射是激光技术诞生的理论基础。
 ,它也具有球面度·米2·赫兹·瓦特-1·秒-1(相当于球面度·米2·焦耳-1·秒-1)的量纲,表征的是在单位时间内辐射场的单位辐射亮度下电子吸收能量为
,它也具有球面度·米2·赫兹·瓦特-1·秒-1(相当于球面度·米2·焦耳-1·秒-1)的量纲,表征的是在单位时间内辐射场的单位辐射亮度下电子吸收能量为 的光子并从低能级
的光子并从低能级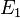 向高能级
向高能级 跃迁的几率。如果假设处在两个能级的原子数密度分别为
跃迁的几率。如果假设处在两个能级的原子数密度分别为 和
和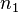 ,则吸收导致的低能级原子数密度
,则吸收导致的低能级原子数密度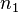 变化率为
变化率为
在热平衡状态下,我们可以假设一个简单的情形,即处于任何激发态的原子的总变化率为零,也就是说通过所有的辐射和吸收过程达到激发态和离开激发态的原子数量保持相等。由于这些跃迁都属于束缚态-束缚态之间的跃迁,我们认为这种平衡是一种细致平衡,也就是说任意两个能级间的总交换保持平衡,这是由于电子跃迁的几率不会受到其他激发态原子存在与否的影响。细致平衡(仅在热平衡状态下成立)要求处于低能级的原子数密度因三种基本过程引起的变化恒定为零:
对麦克斯韦-玻尔兹曼分布我们将原子的任意激发态记作i:
 是包括处于激发态和基态的原子的总数密度;
是包括处于激发态和基态的原子的总数密度; 是玻尔兹曼常数;
是玻尔兹曼常数;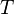 是温度,
是温度, 是激发态i的简并度;
是激发态i的简并度; 是系统的配分函数。根据普朗克黑体辐射定律,我们有在频率
是系统的配分函数。根据普朗克黑体辐射定律,我们有在频率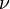 下黑体的辐射亮度为
下黑体的辐射亮度为
 是光速,
是光速, 是普朗克常数。 注意在某些计算中使用的是黑体的能量密度而不是辐射亮度,能量密度的形式为
是普朗克常数。 注意在某些计算中使用的是黑体的能量密度而不是辐射亮度,能量密度的形式为
 可得到
可得到
 和
和 的关系式,这个关系式将普朗克定律蕴含在其中(参见光子#受激辐射和自发辐射)。
的关系式,这个关系式将普朗克定律蕴含在其中(参见光子#受激辐射和自发辐射)。
當上述的高溫氣態等離子體處於熱動平衡狀態,而輻射場能量密度不是太小、氣體密度又是適中的時候,上述的正、反兩類過程就可能逐漸相對穩定,而達到一種嚴格的平衡狀態。也就是:①由於碰撞而從某一能級n上被(再次)電離的原子(或m次電離的離子)數目等於因碰撞而俘獲電子複合到同一能級的原子(或m次電離的離子)數目;②由於吸收適當能量的光子而從某一能級n上被(再次)電離的原子(或m次電離的離子)數目等於俘獲電子後放射出適當能量的光子而複合到同一能級的原子(或m次電離的離子)數目;③由於碰撞,原子(或離子)吸收了一定能量而從能級n被激發到更高能級n'上的數目等於因非彈性碰撞,原子(或離子)失去一定能量而從能級n'下落到能級n上的數目;④由於吸收一定能量的光子,原子(或離子)從能級n受迫躍遷到能級n'的數目等於輻射出一定能量的光子,而從能級n'自發躍遷到能級n的原子(或離子)數目。上述每一種正過程的數目都與它的逆過程的數目相等,這樣的一種平衡狀態便稱為細緻平衡。當高溫氣態等離子體一旦處於細緻平衡狀態時,它肯定就處於熱動平衡狀態,但是,處於熱動平衡狀態的高溫氣態等離子體卻未必處於細緻平衡狀態。
原子谱线[编辑]
维基百科,自由的百科全书
- 吸收谱线是由电子从原子内部离散的特定能级发生跃迁至更高的能级而形成的,这个过程需要吸收具有特定能量和波长的光子。通常情况下这些被吸收的光子会来自一个连续光谱,从而使这个连续光谱在对应被吸收光子的波长处显示出因吸收而凹陷的特征。
跃迁中辐射或吸收的单个光子所携带的能量等于电子跃迁的两个能级之差,用普朗克公式即描述为能级差
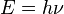 ,其中
,其中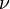 是光子的频率,而
是光子的频率,而 是普朗克常数。
是普朗克常数。发射和吸收系数[编辑]
原子谱线中发射谱线的辐射能量可用一个发射系数 来表示,其含义为单位时间单位体积单位立体角内辐射的能量。由此,
来表示,其含义为单位时间单位体积单位立体角内辐射的能量。由此, 则是在单位时间
则是在单位时间 内从单位体积
内从单位体积 中朝单位立体角
中朝单位立体角 方向上所辐射的能量。对原子发射谱线,发射系数为
方向上所辐射的能量。对原子发射谱线,发射系数为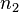 是处于发射状态的原子的数密度,而
是处于发射状态的原子的数密度,而 是自发辐射的爱因斯坦系数,这个系数对于任意两个特定的能级是定值。根据基尔霍夫热辐射定律,空间一定区域内的吸收特性是与它的发射特性密切相连的,因此我们也要同时考虑吸收谱线的吸收系数。吸收系数
是自发辐射的爱因斯坦系数,这个系数对于任意两个特定的能级是定值。根据基尔霍夫热辐射定律,空间一定区域内的吸收特性是与它的发射特性密切相连的,因此我们也要同时考虑吸收谱线的吸收系数。吸收系数 具有“1/长度”的量纲,从而
具有“1/长度”的量纲,从而 给出的是频率为一定的光在行走了距离
给出的是频率为一定的光在行走了距离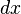 后被吸收的光强占总光强的比例。吸收系数的表达式为
后被吸收的光强占总光强的比例。吸收系数的表达式为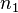 是处于吸收状态的原子的数密度,
是处于吸收状态的原子的数密度, 和
和 分别是爱因斯坦系数中的自发吸收和受激辐射的系数,它们对于任意两个特定的能级也是定值。
分别是爱因斯坦系数中的自发吸收和受激辐射的系数,它们对于任意两个特定的能级也是定值。当系统处于局部的热平衡状态时,处于基态和激发态的原子各自的数密度满足麦克斯韦-玻尔兹曼分布;但对于非热平衡状态的情形(例如激光),原子的数密度分布计算会相当复杂。
上面列出的公式都假设了谱线对应的频率是单一的,即谱线是无形状的几何线,忽略了实际中不确定性原理及多普勒效应等因素造成的谱线展宽,实际的谱线是覆盖一段频率带宽的,具有一定的谱线形状。精确计算时要求这些公式乘以归一化的谱线形状,从而得到带有“1/频率”的量纲。
爱因斯坦系数[编辑]
1916年,阿尔伯特·爱因斯坦指出在原子谱线的形成中存在三种基本过程,它们分别被称作自发辐射、受激辐射和(受激)吸收。每一种过程都对应着一个所谓爱因斯坦系数,表征着该过程所发生的几率。自发辐射[编辑]
自发辐射即是电子在不受外界影响下自发地从高能级向低能级跃迁的过程。描述这一过程的是爱因斯坦系数 ,它具有秒-1的量纲,表征的是在单位时间内电子从高能级
,它具有秒-1的量纲,表征的是在单位时间内电子从高能级 向低能级
向低能级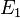 自发跃迁并释放出能量为
自发跃迁并释放出能量为 的光子的几率。由于能量-时间之间的不确定性关系,这一过程产生的光子实际占据了一段很窄的频率范围,即具有一定的线宽。如果假设处在两个能级的原子数密度分别为
的光子的几率。由于能量-时间之间的不确定性关系,这一过程产生的光子实际占据了一段很窄的频率范围,即具有一定的线宽。如果假设处在两个能级的原子数密度分别为 和
和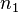 ,则自发辐射导致的低能级原子数密度
,则自发辐射导致的低能级原子数密度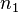 变化率为
变化率为受激辐射[编辑]
受激辐射是指当原子接受到外界的电磁辐射,而外界电磁辐射的频率恰好等于(或接近)电子在某两个能级跃迁时释放光子的频率时,符合这样条件的电子受到激发从高能级向低能级跃迁的过程。描述这一过程的是爱因斯坦系数 ,它具有球面度·米2·赫兹·瓦特-1·秒-1(相当于球面度·米2·焦耳-1·秒-1)的量纲,表征的是在单位时间内辐射场的单位辐射亮度下电子从高能级
,它具有球面度·米2·赫兹·瓦特-1·秒-1(相当于球面度·米2·焦耳-1·秒-1)的量纲,表征的是在单位时间内辐射场的单位辐射亮度下电子从高能级 向低能级
向低能级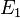 受激跃迁并释放出能量为
受激跃迁并释放出能量为 的光子的几率。如果假设处在两个能级的原子数密度分别为
的光子的几率。如果假设处在两个能级的原子数密度分别为 和
和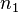 ,则受激辐射导致的低能级原子数密度
,则受激辐射导致的低能级原子数密度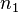 变化率为
变化率为 是辐射场的辐射密度,它是受激频率
是辐射场的辐射密度,它是受激频率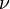 的函数(参见普朗克定律)。
的函数(参见普朗克定律)。受激辐射是激光技术诞生的理论基础。
光吸收[编辑]
吸收是原子吸收光子,使其内部的一个电子从低能级向高能级跃迁的过程。描述这一过程的是爱因斯坦系数 ,它也具有球面度·米2·赫兹·瓦特-1·秒-1(相当于球面度·米2·焦耳-1·秒-1)的量纲,表征的是在单位时间内辐射场的单位辐射亮度下电子吸收能量为
,它也具有球面度·米2·赫兹·瓦特-1·秒-1(相当于球面度·米2·焦耳-1·秒-1)的量纲,表征的是在单位时间内辐射场的单位辐射亮度下电子吸收能量为 的光子并从低能级
的光子并从低能级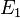 向高能级
向高能级 跃迁的几率。如果假设处在两个能级的原子数密度分别为
跃迁的几率。如果假设处在两个能级的原子数密度分别为 和
和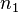 ,则吸收导致的低能级原子数密度
,则吸收导致的低能级原子数密度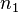 变化率为
变化率为细致平衡[编辑]
爱因斯坦系数对于每一个原子而言代表了确定的跃迁几率,而与原子所组成的气体所处的状态无关。从而,我们在热平衡条件下从这些系数所作的推导具有普适性。在热平衡状态下,我们可以假设一个简单的情形,即处于任何激发态的原子的总变化率为零,也就是说通过所有的辐射和吸收过程达到激发态和离开激发态的原子数量保持相等。由于这些跃迁都属于束缚态-束缚态之间的跃迁,我们认为这种平衡是一种细致平衡,也就是说任意两个能级间的总交换保持平衡,这是由于电子跃迁的几率不会受到其他激发态原子存在与否的影响。细致平衡(仅在热平衡状态下成立)要求处于低能级的原子数密度因三种基本过程引起的变化恒定为零:
对麦克斯韦-玻尔兹曼分布我们将原子的任意激发态记作i:
 是包括处于激发态和基态的原子的总数密度;
是包括处于激发态和基态的原子的总数密度; 是玻尔兹曼常数;
是玻尔兹曼常数;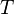 是温度,
是温度, 是激发态i的简并度;
是激发态i的简并度; 是系统的配分函数。根据普朗克黑体辐射定律,我们有在频率
是系统的配分函数。根据普朗克黑体辐射定律,我们有在频率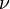 下黑体的辐射亮度为
下黑体的辐射亮度为 是光速,
是光速, 是普朗克常数。 注意在某些计算中使用的是黑体的能量密度而不是辐射亮度,能量密度的形式为
是普朗克常数。 注意在某些计算中使用的是黑体的能量密度而不是辐射亮度,能量密度的形式为 可得到
可得到 和
和 的关系式,这个关系式将普朗克定律蕴含在其中(参见光子#受激辐射和自发辐射)。
的关系式,这个关系式将普朗克定律蕴含在其中(参见光子#受激辐射和自发辐射)。
















No comments:
Post a Comment