Wednesday, August 13, 2014

Landau能级： 电子在磁场中的能量本征值 相应的径向部分的能量本征函数就是Landau波函数 径向偏振光和角向偏振光 在基部的圖樣是向量的矢端隨著時間流易對於xy-平面的投射

[DOC]

第四章中心场定态问题

quantum.ustc.edu.cn/old/teaching/qm2/Q4讲稿.DOC
轉為繁體網頁
或者说，不存在这种状态波函数，它既是的本征态，又是的本征态，等等（有一个例外情况）。 ... 将波函数的径向部分记为，则的方程为 ..... 最后得到能量本征值和本征函数为 .... 另外，还有另一定义，与此处相差一个因子，见朗道《量子力学》，第112页。

  • [PDF]

    2

    quantum.ustc.edu.cn/old/teaching/qm1/q4.pdf
    轉為繁體網頁
    如果H 可以分成互不关联的几部分之和，相应的能量本征值就可. 以分成互 ..... li. 2. ，见朗道《量子力学》，第112 页。 .... 第一，径向波函数方程中不含磁量子数m，于是，.

     

    •  

     

    矩阵_百度文库

    wenku.baidu.com/view/4fd78149fe4733687e21aaca

    轉為繁體網頁
    上节课复习Landau能级： 电子在磁场中的能量本征值E ? (2n? ... 求解相关问题的基本思路： ①根据磁场的特点，写出矢势分量的形式②写出体系的哈密顿③寻找守 
     
     
    一般是指圆柱形物体上受的作用力，该作用力方向通过物体截面的圆心，且垂直于物体的轴线的力，或者球形物体上受的通过球心的力，叫径向力。简单来讲就是：就是作用于直径方向的力
     

    矩阵_百度文库

    wenku.baidu.com/view/4fd78149fe4733687e21aaca

    轉為繁體網頁
    L ? EN Landau波函数： 相应的径向部分的能量本征函数就是Landau波函数Rn? |m| ( ? ) ~ ? |m| F (?n? , | m | ?1, ? 2 ? 2 )e?? 求解相关问题的基本思路： ①根据磁场 ...
     
     
    		产品名称：径向/角向偏振发生器
    所属类别：    径向/角向偏振光发生器
    厂家名称：昊量光电
    产品简介：1064PC是一款针对1064nm激光推出的径向偏振光发生器(Radially Polarization Converter)及角向偏振光发生器（Azimuthally Polarization Converter,方位角偏振光发生器）。1064PC可以将1064nm的线偏振光转转化为径向偏振光（Radially polarized beam）或者角向偏振光（Azimuthally polarized beam）。只需转动入射光的偏振方向，偏振即可在径向偏振光和角向偏振光之间变化，如下图。

    CON1064PC是由12个楔角型半波片组成，每个波片的光轴都相对相邻的前一片旋转15度，如下图。


    我们专利所有的制造及组装技术使得1064PC径向（角向）偏振光发生器可以承受190W/cm2的激光功率。如需任何进一步信息，请和上海昊量光联系



    歷史[编辑]


    艾蒂安-路易·馬呂斯
    丹麥科學家拉斯穆·巴多林（Rasmus Bartholin）於1669年發現了光束通過冰洲石（Iceland spar）時會出現雙折射現象，假設照射光束於冰洲石，則這光束會被折射為兩道光束，一道光束遵守普通的折射定律，稱為「尋常光」，另外一道光束不遵守普通的折射定律，稱為「非常光」。巴多林無法解釋這現象的物理機制。[1]:25後來，克里斯蒂安·惠更斯注意到這奇特現象，他在1690年著作《光論》的後半部裏，對這現象有很詳細的論述；他認為，由於空間可能存在有兩種不同物質，所以才會出現兩道光束，它們分別對應於兩個不同的波前以不同的速度傳播於空間，所以，這不是很不平常的現象，但是，惠更斯又發現，這兩道光束與原本光束的性質大不相同，將其中任何一道光束照射於第二塊冰洲石，則折射出來的兩道光束，其輻照度會因為繞著光束軸旋轉冰洲石而改變，有時候甚至只會剩成一道光束。惠更斯猜想光波是縱波，他想出的簡單波動理論不能對這現象給出解釋。艾薩克·牛頓猜測，雙折射現象意味著組成光束的粒子具有側面（垂直於移動方向）性質。[1]:25-28
    1808年，法蘭西學術院提議，1810年物理獎比賽的題目為"對於雙折射給出數學理論，並且做實驗證實"。艾蒂安-路易·馬呂斯決定參與競爭。他做實驗觀察，日光照射於盧森堡宮的玻璃窗，然後被玻璃反射出來的光束，假若入射角度達到某特定數值，則這反射光與惠更斯觀察到的折射光具有類似的性質，他稱這性質為「偏振」性質。他猜想，組成光束的每一道光線都具有某種特別的不對稱性；當這些光線具有相同的不對稱性時，則光束具有偏振性；當這些光線的不對稱性分別機率地指向不同方向時，則光束具有非偏振性；當在這兩種案例之間時，則光束具有部分偏振性。不單是玻璃，任何透明的固體或液體都會產生這種現象。他又從實驗結果推論出馬呂斯定律，定量地給出偏振光通過檢偏器後的輻照度，考慮到偏振方向與檢偏器傳輸軸方向之間的夾角角度。這實驗極具創意，又得到了很豐碩的重要成果，馬呂思因此榮獲1810年的物理獎。馬呂思對於偏振現象做出諸多貢獻，後人尊稱他為「偏振之父」。[2]:2050-2051[3]:448
    後來，奧古斯丁·菲涅耳與弗朗索瓦·阿拉戈合作研究偏振對於楊氏干涉實驗的影響，他們認為光波是縱波，呈縱向震盪，但是這縱波的概念無法合理解釋實驗結果。阿拉戈告訴托馬斯·楊這問題，托馬斯·楊大膽建議，假若光波是橫波，呈橫向震盪，則光波可以分解為兩個相互垂直的分量，或許這樣做可以對實驗結果給出解釋。果真，這建議清除了很多疑點。1817年，菲涅耳與阿拉戈將實驗結果定性總結為菲涅耳-阿拉戈定律（Fresnel-Arago laws），表述處於不同偏振態的光束彼此之間的干涉性質。之後，菲涅耳試圖進一步定量表述這實驗，他發展出的波動理論是一種振幅表述，主要是用光波的振幅與相位來作分析；振幅表述能夠定量地解釋偏振光的物理性質；但非偏振光或部分偏振光不具有穩定的振幅與相位，無法用振幅表述給予解釋。[4]:xiii-xv[3]:466
    1852年，乔治·斯托克斯提出一種強度表述，能夠描述偏振光、非偏振光與部分偏振光的物理行為；只需要使用四個參數，後來稱為斯托克斯參數（Stokes parameters），就可以描述任何光束的偏振態，更重要地，這四個參數可以直接測量獲得。[4]:xiv-xv
    那時，電磁學理論雜亂無章，詹姆斯·馬克士威將這些理論加以整合，於1865年提出馬克士威方程組。從這方程組，他推導出電磁波方程式，推論出光波是一種電磁波，可以用馬克士威方程組作精確描述。菲涅耳的波動理論是建立於一些貌似合理的假定，由於能夠正確描述光波的一些物理行為，例如，傳播、衍射、偏振等等，符合實驗得到的結果，所以才被學術界接受。從馬克士威方程組可以嚴格地推導出菲涅耳的波動理論，給予這理論堅實穩固的基礎。[4]:2

    理論概述[编辑]


    從白熾燈（1）發射出的非偏振光（2）入射於傳輸軸為垂直方向的起偏器（3），透射出來的是垂直平面偏振光（4）。
    大多數光源屬於非偏振光源，例如，太陽、白熾燈等等，因為它們所發射出的光波是由一組不同空間特徵、頻率（波長）、相位、偏振的光波隨機混合所組成。為了了解光波的偏振性質，最簡單的方法就是先只思考單色平面波，這種波是具有特定傳播方向、頻率、相位、振盪方向的正弦波。從研究平面波光學系統的性質與行為，可以對於一般案例給出預測，這是因為任何特定空間結構的光波都可以分解為一組不同頻率、不同振幅的平面波，稱為其角譜（angular spectrum）。[5]:55ff

    橫電磁波[编辑]


    傳播於自由空間的電磁波是橫波，電場方向與磁場方向彼此相互垂直，又都垂直於傳播方向。
    光波是一種電磁波。在自由空間裏，電磁波是橫波，其電場與磁場的方向都垂直於電磁波的傳播方向，並且相互垂直。[註 1]}}設想一個頻率為f的電磁平面波朝著+z-軸方向傳播，電磁波的電場 \mathbf{E}(z,t)、磁場 \mathbf{B}(z,t) 必定平行於xy-平面，以方程表示為[7]:295-299[5]:64-65
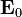    \mathbf{E}(z,t) = \mathbf{E}_0 e^{i(kz - 2 \pi f t)}=(\hat{x}E_{0x}+\hat{y} E_{0y}) e^{i(kz - 2 \pi f t)}、
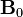    \mathbf{B}(z,t) = \mathbf{B}_0 e^{i(kz - 2 \pi f t)}=(\hat{x}B_{0x}+\hat{y} B_{0y}) e^{i(kz - 2 \pi f t)}；
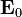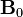    其中，\mathbf{E}_0與\mathbf{B}_0分別是複常數向量，k是波數。
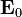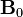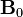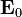    \mathbf{E}_0的x-分量、y-分量分別描述電磁波的電場朝著x方向、y方向的振輻；類似地，\mathbf{B}_0的x-分量、y-分量分別描述電磁波的磁場朝著x方向、y方向的振輻。對於這朝著+z-軸方向傳播的橫電磁波，\mathbf{E}_0與\mathbf{B}_0的z-分量都等於0。\mathbf{B}_0與\mathbf{E}_0之間的關係為
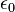    \mathbf{B}_0 =\sqrt{\mu_0 \epsilon_0}\hat{z}\times\mathbf{E}_0；
    其中，\epsilon_0為電常數，\mu_)為磁常數。
    所以，從電磁波的電場可以計算出磁場。
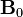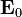    類似地，在簡單介質裏，\mathbf{B}_0與\mathbf{E}_0之間的關係為[註 2]
    \mathbf{B}_0 =\sqrt{\mu\epsilon}\hat{z}\times\mathbf{E}_0；
    其中，\epsilon為電容率，\mu為磁導率。
    所以，儘管電磁波傳播於簡單介質，仍舊可以從電磁波的電場計算出磁場。
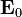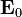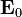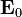    由於\mathbf{E}_0是常數向量，不會隨著時間的流易而改變方向，所以，這電磁波具有偏振性質，偏振方向是\mathbf{E}_0的方向，偏振平面是\mathbf{E}_0與z-軸共同組成的平面。由\mathbf{E}_0的x-分量、y-分量所組成的向量稱為瓊斯向量，可以用來描述偏振。除了給定偏振以外，瓊斯向量還給定了整體電磁波的大小與相位。[6]:376-377特別而言，電磁波的輻照度I以方程表示為
    I = (|E_{0x}|^2 + |E_{0y}|^2) /2 \eta ；
    其中，\eta=\sqrt{\mu/\epsilon}是這簡單介質的特性阻抗（characteristic impedance）
    偏振與兩個分量的比率有關，在解析偏振問題時，可以約化為只思考|E_{0x}|^2+|E_{0y}|^2=1的電磁波，將電磁波歸一化；偏振與兩個分量的相對向位有關，因此可以設定E_{0x}的相位為零，換句話說，約化為只思考E_{0x}是實數，E_{0y}是複數的偏振問題，E_{0x}、E_{0y}分別表示為
    E_{0x} = \sqrt{\frac{1+Q}{2}} 、
    E_{0y} = \sqrt{\frac{1-Q}{2}} \, e^{i \phi} ；
    其中，Q、\phi是偏振態的兩個參數，-1\le Q \le 1。
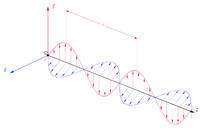
    按照常規，當提到偏振時，假若沒有特別設定，通常指的是電場的偏振。磁場的偏振通常與電場類似，唯一不同之處是90°空間角度差。

    偏振態[编辑]

    線偏振
    圓偏振
    橢圓偏振
    電場向量隨著時間（z-軸）流易而演變。電場向量以黑色粗線表示，它的x-分量、y-分量分別以紅色細線、藍色細線表示。在基部的圖樣是向量的矢端隨著時間流易對於xy-平面的投射。
    在正弦波的每一個周期，電場向量和磁場向量都會描繪出一個橢圓形（注意到線偏振與圓偏振是橢圓偏振的特別案例）。這橢圓的形狀與定向定義了電磁波的偏振態。右圖展示出幾種不同種類的偏振。假設電場的x-分量、y-分量完全同相，則隨著時間流易，電場向量的矢端對於xy-平面的投射，會描繪出一條直線段，這案例因此稱為「線偏振」，又稱為「平面偏振」。假設電場的x-分量、y-分量擁有同樣的振輻，但是失相90°，則隨著時間流易，電場向量的矢端對於xy-平面的投射，會描繪出一條圓圈，這案例因此稱為「圓偏振」。根據光學領域常規，依相位差為-90°或+90°，圓偏振又分為右旋圓偏振（順時針旋轉）或左旋圓偏振（逆時針旋轉）。[6]:327-328假設除了失相以外，兩個分量的振輻不同，則隨著時間流易，電場向量的矢端對於xy-平面的投射，會描繪出一條橢圓，這案例因此稱為「橢圓偏振」。類似地，對應於不同的偏振態，電場的順時針旋轉或逆時針旋轉可以製成同樣的橢圓形狀。[8]:25-28
    只要光波的傳播方向與z-軸同向，而xy-平面的定向可以任意選擇，就能夠正確地表現每一種偏振態。在解析問題時，通常會選擇合適的坐標軸，例如，光波的入射方向與x-軸同平面。另外，任意兩個相互正交的偏振態可以設定為基底函數；這樣，任意偏振態可以用基底函數來表示，例如，設定兩個相互正交的線偏振態為基底函數，則可很自然地處理表面反射、雙折射等問題。右旋圓偏振態與左旋圓偏振態也是很有用的選擇，可以用來研究光波傳播於立體異構的問題。[9]:49-50

    非偏振光[编辑]

    可見光的大多數常見光源，包括黑體輻射、螢光等，會發射出不相干光波。在這些光源物質裏，處於激發態的原子或分子會獨立、毫無關聯地發射出這些隨機偏振的電磁輻射波列。每個波列持續大約10-8秒，所以，光波的偏振只能保持不變不超過10-8秒。這種光波稱為「非偏振光」。這術語所傳達出的意思並不精準，因為在任意時刻、任意位置，電場與磁場的方向都很明確，這術語所要傳達出的意思為，偏振隨時間流易而改變的速度非常快，它不是無法被測量到，就是與實驗結果無關。偏振光在通過消偏器（英语：Depolarizer (optics)）（depolarizer）之後，由於透射光的偏振隨時間流易而改變的速率非常快，實際而言，可以忽略透射光在任意時刻的偏振，因此將透射光歸類為「非偏振光」。
    假若光波的一個偏振模的功率與另一個偏振模的功率不一樣，則可稱此光波為「部分偏振光」。它可以統計描述為一個完全非偏振光與一個完全偏振光的疊加。[6]:330偏振度（degree of polarization）是光波的偏振部分所佔有的百分比，可以用來描述光波的成分。部分偏振態最常用斯托克斯参量（Stokes parameters）來設定。[6]:351,374-375

    其它種類偏振[编辑]


    上图是角向偏振，下图是径向偏振。
    除了橫波以外，很多種波動的振盪方向不局限為垂直於傳播方向。這些案例超過本條目範疇，本條目專注於橫波，可是，在有些案例裏，相干波的偏振不能簡單地用瓊斯向量或斯托克斯向量描述。
    設想先前提到的傳播於均勻、各向同性、非衰減性介質的電磁平面波，假設改為傳播於各向異性介質，例如雙折射晶體，電場或磁場可能還會擁有縱場。對於這種案例，因為介質具有各向異性，它的電極化率或磁導率必需用張量來描述，電場的方向可能不同於電位移的方向，磁場強度的方向可能不同於磁場的方向。[10]:179-184[11]:51-52有些各向同性介質的折射率是複數，折射率的很大一部分是虛數，例如，金屬。甚至在這些介質裏，非均勻波都可以傳播；嚴格而說，它的各個場並不完全是橫場。表面波、傳播於波導或光纖的電磁波通常不是橫波，但是可以以橫模（transverse mode）的概念來描述。橫模又分為「橫電模」、「橫磁模」、「橫電磁模」、「混合模」四種。[10]:405-408
    在自由空間裏，縱場分量可以被生成於平面波近似不成立的焦區。舉一個極端例子，在徑向偏振（radial polarization）光或角向偏振（azimuthal polarization）光的焦點，電場與磁場完全是縱場，與傳播方向同向。[12]

    引力波的十字型偏振h+與交叉型偏振h×對於排列成圓圈形狀的粒子所產生的振盪效應

    Posted by at

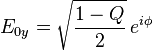    No comments:

    Post a Comment

    Subscribe to: Post Comments (Atom)