物理数学好图 正则对易关系 海森堡 一个量是其共轭量的傅立叶转换的结果
正则对易关系
物理学中,正则对易关系是正则共轭的量之间的关系,这样的量从定义可以发现:一个量是其共轭量的傅立叶转换的结果。举例来说:
 为约化普朗克常数,等于h / 2π。此一关系常归功于 海森堡,并且此式子暗示了以海森堡为名的不确定性原理。
为约化普朗克常数,等于h / 2π。此一关系常归功于 海森堡,并且此式子暗示了以海森堡为名的不确定性原理。
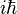 换成1:
换成1:
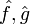 应满足
应满足
维基百科,自由的百科全书
物理学中,正则对易关系是正则共轭的量之间的关系,这样的量从定义可以发现:一个量是其共轭量的傅立叶转换的结果。举例来说:
 为约化普朗克常数,等于h / 2π。此一关系常归功于 海森堡,并且此式子暗示了以海森堡为名的不确定性原理。
为约化普朗克常数,等于h / 2π。此一关系常归功于 海森堡,并且此式子暗示了以海森堡为名的不确定性原理。[编辑] 与经典力学的关系
相对于量子力学,经典物理中所有可观测量都可对易(交换),而交换算符会是零;然而仍然有类似的关系存在:需将交换子换成泊松括号,且常数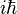 换成1:
换成1: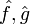 应满足
应满足![[\hat f,\hat g]= i\hbar\widehat{\{f,g\}} \,](http://upload.wikimedia.org/math/d/b/6/db6ae61d89368729bfc997c657b20f76.png) 。
。
![[x,p] = i\hbar](http://upload.wikimedia.org/math/3/3/1/3315cfa4d6b0728b9fdb59593c67fa63.png)

No comments:
Post a Comment