Proc Natl Acad Sci U S A. Mar 31, 1998; 95(7): 4072–4075.
PMCID: PMC19965
Economic Sciences
The Black–Scholes pricing formula in the quantum context
Abstract
A natural explanation for extreme irregularities in the evolution of prices in financial markets is provided by quantum effects. The lack of simultaneous observability of relevant variables and the interference of attempted observation with the values of these variables represent such effects. These characteristics have been noted by traders and economists and appear intrinsic to market dynamics. This explanation is explored here in terms of a corresponding generalization of the Wiener process and its role in the Black–Scholes–Merton theory. The differentiability of the Wiener process as a sesquilinear form on a dense domain in the Hilbert space of square-integrable functions over Wiener space is shown and is extended to the quantum context. This provides a basis for a corresponding generalization of the Ito theory of stochastic integration. An extension of the Black–Scholes option pricing formula to the quantum context is deduced.
Keywords: Brownian motion, quantum process, stochastic integration, Ito lemma, Black–Scholes–Merton theory
In the past several decades, the role of information in economics has expanded greatly, and it now is recognized as a dominant factor in several areas, most notably financial markets. Imperfect information appears especially as the culprit that may defeat earlier rational process analysis. But beyond this, it is clear that there are many contexts in economics in which information is not merely lacking but in which this is inherently and fundamentally the case. The information on several relevant factors—consumer preferences and technological capability, e.g.—may be not simply missing but lacking in simultaneous observability. Attempts to observe the missing information may react on and alter complementary information.
These features characterize a quantum system in the mathematical sense, to which is applicable von Neumann’s general treatment (1) of observables and states, as well as the philosophical ideas of “complementarity” due to Bohr and of “indeterminacy” due to Heisenberg. In particular, one of the most evident features of a financial market is the impossibility of observing prices and their instantaneous forward time derivatives. This quite fundamental aspect is not captured in the conventional formalism in which both quantities are represented as random variables. Conventional random variables are in principle simultaneously observable, whereas a lack of simultaneous observability appears capable of precise mathematical formulation only in quantum terms.
The literature treating the general importance of factors outside the realm of public information for market dynamics includes works of traders and economists, e.g., the books of Keynes (2) and Soros (3) and of Grossman (4) and Shiller (5). A quite small sampling of the extensive journal literature on specific aspects includes Delong et al. (6), Grossman and Stiglitz (7), Lo and MacKinlay (8), Lo and Wang (9), and Poterba and Summers (10).
The classical (= unquantized) theory of prices in financial markets that originated with Black and Scholes (11) and Merton (12) (hereafter, BSM theory) has been highly successful and is widely accepted. A quantum variant of this theory serves to facilitate the modeling of phenomena not fully explained by it, such as short-term volatility, extreme discontinuities, serial correlation, and notably large-tailed distributions.¶ At the same time, it provides a formal mathematical basis for the reconciliation in principle of the market rationality hypothesis with empirically based literature such as that cited, and trading practices productive of asymmetric information, such as front-running in one form or another.
The simplest version of such a theory probably consists of the substitution of a quantum process for the Wiener process that underlies the BSM theory. However, this substitution requires the associated development of a theory of integration that appropriately extends the Ito theory (13). This article presents this development and applies it to the derivation of a quantum version of the Black–Scholes option pricing formula.
Random Variables in the Quantum Context
The mathematical foundations of probability theory due to Kolmogoroff represent random variables as measurable functions on a measure space M. The operation of multiplication by a measurable function, acting on the Hilbert space H of all square-integrable functions over the measure space, is then a self-adjoint operator in H. Conversely, any self-adjoint operator in H is (unitarily) equivalent to the operation of multiplication by a measurable function.
The operations of multiplications on H by measurable functions on M are mutually commutative. In the quantum context, (generalized) random variables are represented by self-adjoint operators and differ from those of conventional probability theory essentially only in that they need not commute. Indeed, they are mutually commutative if and only if they are simultaneously observable or, in mathematical terms, simultaneously representable as multiplications by measurable functions.
A classic physics example is that of the ensembles of the particle and field strength observables of light. Each ensemble by itself consists of mutually commutative observables, but the two ensembles do not commute with each other. The quantized light field as a unified entity is mathematically perfectly well defined and entirely explicit, notwithstanding its anthropomorphically unintuitive features, and serves to reconcile simply and effectively the corpuscular and wave aspects of light.
Probability theory is equivalent in all observable aspects to just that special case of a quantum system, modeled as an ensemble of self-adjoint operators together with an expectation value form on the ensemble, in which there is full simultaneous observability. This follows from commutative spectral theory, according to which any ensemble of commuting self-adjoint operators is unitarily equivalent to a corresponding ensemble of multiplications by measurable functions acting on the space of square-integrable functions over a measure space. An “expectation value functional” E on the ensemble satisfying the basic constraints of linearity and positivity (hereafter, simply “state,” for brevity and positivism) then corresponds to integration over the measure space, and conversely.
This formulation of a system of observables may be rationalized by postulates applicable to quantitative science in general and not only to physics. For brevity, however, we define here simply a “quantum system” (A, E, H) as one consisting of a linear ensemble A of self-adjoint operators in the Hilbert space H that is closed under addition and the “Jordan” product AoB = (AB + BA)/2, together with a linear functional E on A satisfying the constraints (positivity and normalization) that E(A2) ≥ 0 for all A in A, and E(I) = 1, where I denotes the identity operator (i.e., E is a state in the sense given above). The Jordan product is used because the product AB of observables A and B is definable in observable terms (and is self-adjoint) only when they are simultaneously observable, which is equivalent to their commutativity. In particular, A2 is definable, which implies that AoB is definable because it may be expressed as [(A + B)2 − A2 − B2]/2. (As argued by von Neumann, the sum A + B is definable by virtue of the linearity of E, which permits A + B to be defined as that observable such that E(A + B) = E(A) + E(B) in all states of the system.)
Quantum effects may be incorporated directly into the BSM analysis by the addition to the Wiener process W(t) representing the evolution of public information affecting the market of a distinct process X(t) representing the influence of factors not contemporaneously observable with those involved in W(t). X(t) may in itself also be equivalent to a Brownian motion, but the conjunction of W(t) with X(t) cannot be represented as simply a two-dimensional Brownian motion process.
Some degree of specification of the nature of the lack of simultaneous observability is naturally required for mathematical development. The absence of simultaneous observability for two observables A and B is represented mathematically by the nonvanishing of the commutator AB-BA. In the absence of a priori information on the commutators of the W(t) with the X(t′), it appears reasonable to assume that they are constants dependent on t and t′, to a first approximation.
To set up an explicit simultaneous mathematical representation for both processes that incorporates such features, it is natural to use the formalism of the quantum theory of systems of an infinite number of degrees of freedom, i.e., the quantum field theory. The Wiener process as well as the quantum processes treated below may in fact be given simple mathematical forms in these terms. The (free boson) quantum field over a given Hilbert space H (e.g., see ref. 14), consists of a structure (K, Φ, Γ, v) in which K is a Hilbert space, Φ is a mapping from vectors in H to self-adjoint operators in K, Γ is a continuous mapping from the unitary operators on H into those on K, and v is a unit vector in K, which is uniquely characterized by the following properties:
(i) The “Weyl” (or “canonical commutation”) relations: for arbitrary x, y in H, exp(iΦ(x))exp(iΦ(y)) = exp(iΦ(x + y))exp(iIm<x, y>/2).
(ii) The liftup of transformations on H to those on K: if U is a unitary operator on H and x is a vector in H, then Γ(U)Φ(x)Γ(U)* = Φ(Ux); Γ(U)v = v; and the self-adjoint generator of the unitary one-parameter group Γ(eit) is positive.
(iii) Minimality of K: the linear combinations of the exp(iΦ(x))v (x arbitrary in H) are dense in K.
The vector v represents the “vacuum” state of the quantum field, in which the expectation value E(A) of a self-adjoint operator A in K takes the form <Av, v>. The vacuum state is invariant under Γ(U) for an arbitrary unitary operator U on H, but there are other states with this property of “universal” invariance, including in practice temporal invariance, which is characteristic of an equilibrium state. The most general ergodic (or “pure”) universally invariant state (15), denoted Eγ, is that whose generating function E[exp(iΦ(x))] takes the form exp(−γ2∥ x ∥2/4), where γ is a constant ≥1. (γ = 1 corresponds to the vacuum state; values of γ < 1 are not consistent with positivity.)
Temporal invariance considerations are simplified by treating processes on the entire real line, rather than on an interval or half-axis (see, e.g., refs. 16 and 17). A quantum point (resp. interval) process will be defined as a map from a real interval (resp., an additive map from the subintervals thereof) to the operators of a quantum system (A, E, H). For example, if t → ft is a map from 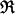 to functions on H = L2(
to functions on H = L2(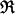 ), then the map t → Φ(ft) from
), then the map t → Φ(ft) from 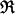 to self-adjoint operators in the quantum field Hilbert space K is a quantum point process, relative to any given state E. The map (a, b) → Φ(fb − fa) from intervals (a, b) (with a < b) on
to self-adjoint operators in the quantum field Hilbert space K is a quantum point process, relative to any given state E. The map (a, b) → Φ(fb − fa) from intervals (a, b) (with a < b) on 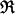 to the self-adjoint operators is the associated quantum interval process.
to the self-adjoint operators is the associated quantum interval process.
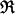 to functions on H = L2(
to functions on H = L2(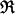 ), then the map t → Φ(ft) from
), then the map t → Φ(ft) from 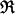 to self-adjoint operators in the quantum field Hilbert space K is a quantum point process, relative to any given state E. The map (a, b) → Φ(fb − fa) from intervals (a, b) (with a < b) on
to self-adjoint operators in the quantum field Hilbert space K is a quantum point process, relative to any given state E. The map (a, b) → Φ(fb − fa) from intervals (a, b) (with a < b) on 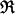 to the self-adjoint operators is the associated quantum interval process.
to the self-adjoint operators is the associated quantum interval process.
In the state Eγ, if x1, … xn is any set of real vectors in H, then the (commutative observables) Φ(x1), Φ(xn) are normally distributed with vanishing means and covariance matrix ½γ2∥<xi, xj>∥). In particular, if ct denotes the characteristic function of the interval [0, t], then for t ≥ 0, Φ(ct) is equivalent to a Wiener process on the positive half-axis of variance parameter ½γ2. The corresponding interval process is then defined on all finite intervals in 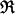 and is temporally stationary, as a consequence of the universal invariance of the Eγ. Thus, the unitary transformation U(t): f(x) → f(x + t) in H induces the unitary transformation Γ(U(t)) in K, and this is equivalent to the transformation of random variables on Wiener space x(J) → x(J + t) where x(J) denotes the increment in the Wiener process over the interval J. The space of all square-integrable random variables on Wiener space for the full line is correspondingly equivalent to K by a unitary transformation that carries the function identically 1 on Wiener space into v.
and is temporally stationary, as a consequence of the universal invariance of the Eγ. Thus, the unitary transformation U(t): f(x) → f(x + t) in H induces the unitary transformation Γ(U(t)) in K, and this is equivalent to the transformation of random variables on Wiener space x(J) → x(J + t) where x(J) denotes the increment in the Wiener process over the interval J. The space of all square-integrable random variables on Wiener space for the full line is correspondingly equivalent to K by a unitary transformation that carries the function identically 1 on Wiener space into v.
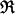 and is temporally stationary, as a consequence of the universal invariance of the Eγ. Thus, the unitary transformation U(t): f(x) → f(x + t) in H induces the unitary transformation Γ(U(t)) in K, and this is equivalent to the transformation of random variables on Wiener space x(J) → x(J + t) where x(J) denotes the increment in the Wiener process over the interval J. The space of all square-integrable random variables on Wiener space for the full line is correspondingly equivalent to K by a unitary transformation that carries the function identically 1 on Wiener space into v.
and is temporally stationary, as a consequence of the universal invariance of the Eγ. Thus, the unitary transformation U(t): f(x) → f(x + t) in H induces the unitary transformation Γ(U(t)) in K, and this is equivalent to the transformation of random variables on Wiener space x(J) → x(J + t) where x(J) denotes the increment in the Wiener process over the interval J. The space of all square-integrable random variables on Wiener space for the full line is correspondingly equivalent to K by a unitary transformation that carries the function identically 1 on Wiener space into v.
The operators Φ(f) are mutually commutative if the f are restricted to be real functions in H, and the same is true of the operators Φ(if), but [Φ(f), Φ(ig)] = i<f, g> if f and g are real. Moreover, the Φ(ict) also form a Wiener process apart from nomenclature. Thus, Φ(ict) is a natural candidate for the quantum information process X(ct) considered above, and the combined processes “aW(t) + bX(t)” may be represented as Φ((a + ib)ct). The present method is simply applicable to a considerably more general class of processes, including those with serial correlation, such as the Ornstein–Uhlenbeck (O–U) process suggested as a model for certain markets (see, e.g., ref. 9). The next section defines this class and shows that these processes are differentiable in a generalized sense, on which their integration theory is later based.
Differentiation of Quantum Processes
We define a pseudo-Wiener process (hereafter, PSW) as a point map t → Φ(ft), or corresponding interval map [a, b] → Φ(fb − fa), provided the following conditions are satisfied:
(i) The map t → ft is continuous from the reals to H;
(ii) <ft, fs> is left-differentiable as a function of t, for arbitrary fixed s, with a uniformly bounded left derivative;
(iii) For all t, limh→0 h−1∥ft+h − ft∥2 (≡ k(t)) exists;
(iv) <ft, g> is left-differentiable as a function of t for arbitrary functions g in the domain Do of infinitely differentiable functions on 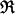 for which all derivatives are square-integrable.
for which all derivatives are square-integrable.
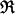 for which all derivatives are square-integrable.
for which all derivatives are square-integrable.
These conditions are weak in practice and are evidently satisfied in simple cases such as the classical Wiener or O–U processes. In the latter cases, the functions ft are real-valued whereas in the quantum case they in general are complex-valued. In the application to markets, the real part of ft may be interpreted as a representation of the public information process, and the imaginary part represents information that is not observable contemporaneously with the public information.
Differentiation and integration theory for quantum processes is facilitated by correlating the process values with sesquilinear forms on a dense domain D of sufficiently regular vectors in K. Any operator A having D in its domain determines (and may thereby be identified with) a form fA by the equation fA(x, y) = <Ax, y>. In general, sesquilinear forms on D will not arise from operators in this way, and their product is undefined. However, forms have adjoints, and their products with an operator (in either order) is defined, provided the operator and its adjoint leave D invariant. Thus, f*(x, y) = f(y, x)*, where for a complex number a, a* denotes the complex conjugate; and (fB)(x, y) = f(Bx, y), (Bf)(x, y) = f(x, B*y), if f is a given form and B a given operator. Operators may thereby be naturally identified with a special class of forms.
Φ(f) is an unbounded operator except when f = 0, and its domain requires constraint. Let D1 denote the domain in K consisting of the linear combinations of the vectors of the form Φ(f1) …
… Φ(fn)v, where the fj are in Do. Any PSW V(t) determines a corresponding form-valued function
Φ(fn)v, where the fj are in Do. Any PSW V(t) determines a corresponding form-valued function ![[var phi]](http://www.ncbi.nlm.nih.gov/corehtml/pmc/pmcents/x03C6.gif) t of t by the equation
t of t by the equation ![[var phi]](http://www.ncbi.nlm.nih.gov/corehtml/pmc/pmcents/x03C6.gif) t(x, y) = <V(t)x, y>, and this function is differentiable. This implies in particular the differentiability of the Wiener process as a form on D1. However, D1 need not be invariant under the V(t) or smooth functions thereof. To attain this property, D1 will be enlarged to the domain D consisting of all linear combinations of the F1(V(t1)) …
t(x, y) = <V(t)x, y>, and this function is differentiable. This implies in particular the differentiability of the Wiener process as a form on D1. However, D1 need not be invariant under the V(t) or smooth functions thereof. To attain this property, D1 will be enlarged to the domain D consisting of all linear combinations of the F1(V(t1)) … Fn(V(tn))y where y is arbitrary in D1 and the Fj are in the space F of C3 functions on
Fn(V(tn))y where y is arbitrary in D1 and the Fj are in the space F of C3 functions on 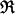 , which, together with their first three derivatives, are O(exp(xa)) with a < 2. In D, differentiability is only one-sided, but this is sufficient for present purposes.
, which, together with their first three derivatives, are O(exp(xa)) with a < 2. In D, differentiability is only one-sided, but this is sufficient for present purposes.
 …
… Φ(fn)v, where the fj are in Do. Any PSW V(t) determines a corresponding form-valued function
Φ(fn)v, where the fj are in Do. Any PSW V(t) determines a corresponding form-valued function ![[var phi]](http://www.ncbi.nlm.nih.gov/corehtml/pmc/pmcents/x03C6.gif) t of t by the equation
t of t by the equation ![[var phi]](http://www.ncbi.nlm.nih.gov/corehtml/pmc/pmcents/x03C6.gif) t(x, y) = <V(t)x, y>, and this function is differentiable. This implies in particular the differentiability of the Wiener process as a form on D1. However, D1 need not be invariant under the V(t) or smooth functions thereof. To attain this property, D1 will be enlarged to the domain D consisting of all linear combinations of the F1(V(t1)) …
t(x, y) = <V(t)x, y>, and this function is differentiable. This implies in particular the differentiability of the Wiener process as a form on D1. However, D1 need not be invariant under the V(t) or smooth functions thereof. To attain this property, D1 will be enlarged to the domain D consisting of all linear combinations of the F1(V(t1)) … Fn(V(tn))y where y is arbitrary in D1 and the Fj are in the space F of C3 functions on
Fn(V(tn))y where y is arbitrary in D1 and the Fj are in the space F of C3 functions on 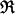 , which, together with their first three derivatives, are O(exp(xa)) with a < 2. In D, differentiability is only one-sided, but this is sufficient for present purposes.
, which, together with their first three derivatives, are O(exp(xa)) with a < 2. In D, differentiability is only one-sided, but this is sufficient for present purposes.
Theorem 1. <V(t)u, u′> is a left-differentiable function of t, for arbitrary fixed u and u′ in D.
The proof uses the fact that E(AB) = E(A)E(B) if A and B are functions of the Φ(x) with the x ranging over respective orthogonal submanifolds of H. It uses also the simultaneous spectral resolution of the F(x) for real x, in terms of an infinite sequence of independent identically distributed Gaussian random variables (14). The complex vectors in Do may be eliminated from the definition of D1 by repeated use of the canonical commutation relations and the fact that, for real f, Φ(if)v = −iΦ(f)v. Given u and u′ in D1 may be expressed in terms of the application of Φ to a finite-dimensional submanifold of H. Applying the Gram–Schmidt process to a basis for the manifold spanned by this submanifold together with the ft then expresses <V(t)u, u′> as a linear combination of Gaussian integrals whose only dependence on t is via external coefficients of the form <ft, g> with g either in Do or of the form fs.
The boundedness and the continuity of the left derivatives of the <ft, g>, except at the point t = s when g = fs, implies also
Corollary 1. For arbitrary u and u′ in D, <W(t)u, u′> is a continuous as well as left-differentiable function of t. Moreover, the left derivative is uniformly bounded and continuous with the possible exception of a finite number of t-values in any finite interval.
Integration of Quantum Processes
For a given PSW W(t), the left derivative of W(t) as a form on the domain D will be denoted as w(t). The product of the form w(t) with the self-adjoint operator F(W(t)) leaving D invariant is defined for F in F, making possible the definition of the integral ∫0t F(W(s))w(s)ds as the weak integral J given by the equation <Ju, u′> = ∫<F(W(s))w(s)u, u′>ds.
The quantum extension of Ito’s formula for F(W(t)) involves the derivative of F as a function of noncommuting operators, which is in general not simply F′. To avoid technicalities extraneous to ideational aspects of financial markets, F will now be limited to be of the form F(x) = ∫exp(ax)dG(a), where the integration is over all of 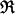 , and G is locally of bounded variation and such that the integrals representing F, F′, and F′′ are absolutely convergent. This class of functions will be denoted as Fo, and the domain D will be redefined by restricting the functions F in the earlier definition of D to be in Fo. The following result extends Ito’s lemma for this extensive and adequate class of functions and implies that the indicated weak integral effectively coincides with stochastic integration in the usual sense.
, and G is locally of bounded variation and such that the integrals representing F, F′, and F′′ are absolutely convergent. This class of functions will be denoted as Fo, and the domain D will be redefined by restricting the functions F in the earlier definition of D to be in Fo. The following result extends Ito’s lemma for this extensive and adequate class of functions and implies that the indicated weak integral effectively coincides with stochastic integration in the usual sense.
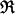 , and G is locally of bounded variation and such that the integrals representing F, F′, and F′′ are absolutely convergent. This class of functions will be denoted as Fo, and the domain D will be redefined by restricting the functions F in the earlier definition of D to be in Fo. The following result extends Ito’s lemma for this extensive and adequate class of functions and implies that the indicated weak integral effectively coincides with stochastic integration in the usual sense.
, and G is locally of bounded variation and such that the integrals representing F, F′, and F′′ are absolutely convergent. This class of functions will be denoted as Fo, and the domain D will be redefined by restricting the functions F in the earlier definition of D to be in Fo. The following result extends Ito’s lemma for this extensive and adequate class of functions and implies that the indicated weak integral effectively coincides with stochastic integration in the usual sense.
Theorem 2. Let F be arbitrary in Fo. Then F(W(t)) = F(0) + ∫0t [F′(W(s))ow(s) + k(s)F′′(W(s))]ds.
The proof follows from the theorem of Scheefer (18) according to which continuous functions whose left derivatives coincide with the possible exception of a countable set of points differ only by a constant. Each side of the foregoing equation is both continuous and left differentiable as a function of t. To evaluate the derivative of the left side, consider first the case F(x) = exp(ax). The corresponding difference quotient simplifies via the extension of the Weyl relations to the exp(Φ(x)), which are unbounded but defined on D. Wick’s theorem on the expectation values of products of quantum fields extends to the states Eγ and shows that effects of order higher than the second give vanishing contributions. The derivative of the right side is immediate from the definition of the integral and coincides with that of the left side. The case of general F in Fo follows from the linearity in F of both sides of the conclusion.
Example: The conventional equation for the temporal evolution of a stock price P(t) requires only the use of the Jordan product to adapt to the present context, together with the use of forms. The stochastic exponential of a quantum process P(t) may be defined as the solution of the integral equation E(t) = 1 + ∫0tP′(s)oE(s)ds. Theorem 2 shows that, if P(t) = r + w(t), then E(t) = exp[rt + W(t) − ½kt].
The Black–Scholes Formula
The derivation in the present context is based on the usual simplifying assumptions regarding market dynamics, notably the absence of riskless arbitrage possibilities. It is assumed also that there is no friction or dividends, that there is a riskless interest rate r, and that short selling is unrestricted, trading is continuous, and securities are infinitely divisible. For simplicity, the basic parameters are assumed constant (the method extends to the case when they are given functions of t). Stock prices are assumed to satisfy the equation of Corollary 2.
The Feynman–Kac formula in the noncommutative form based on ref. 19 is then applicable by the same argument as in the classical case (20). If g is the terminal value function, r is the riskless interest rate, T the elapsed time, and P(t) the stock price process, the value V of the option takes the natural form of the expected discounted payoff, after replacement of the stock price process with a conceptual process having the modified drift rP(t): V = Ed[e−rTg(P(T))].
The normal distribution of Φ(x) whose characteristic functions is given above implies a corresponding lognormal distribution for the price change over the interval [0, T] of mean T(r − k/2) and variance ½g2∥fT∥2, noting that Φ(x) is normally distributed with vanishing mean and variance ½g2∥x∥2. V may accordingly be expressed as a Gaussian integral, which in the case of a European call option with initial price P and strike price K takes the following form, in terms of the parameter s = ||fT|| /T1/2 generalizing the classical volatility:
/T1/2 generalizing the classical volatility:


 where N(x) = (2π)−1/2 ∫0x exp(−y2/2)dy.
where N(x) = (2π)−1/2 ∫0x exp(−y2/2)dy.
 /T1/2 generalizing the classical volatility:
/T1/2 generalizing the classical volatility:
The classical formula is obtained by the substitutions γ = 1, s = σ, k = σ2. The formula involves two additional parameters beyond the volatility, in the usual case in which ft = ct, but γ and s occur only in the combination γs. They could be estimated separately by a determination of the expectation functional for prices conditional on an objective quantitative designation of “public” information. For models with serial correlation, k typically vanishes. It should be interesting to test empirically whether in fact k = s2 as in the Wiener process model or k = 0 as typically in processes with serial correlation.
The results for options involving multiple times or time-dependent parameters may be expected to show greater differences between the classical and quantum cases because of the generic noncommutativity of the quantum prices at several future times. Analytic estimates show that when T is sufficiently large, increases in γ while holding the other parameters constant correspond to a greater prevalence of irregularities.
Summary
The quantum extension of the Black–Scholes–Merton theory provides a rational, scientifically economical, and testable model toward the explanation of market phenomena that show greater extreme deviations than would be expected in classical theory. The volatility estimated from daily prices on the time of months may be expected to correspond roughly to γs. γ is interpretable as a measure of market entropy, deriving from factors separate from price volatility, e.g., trading volume. On the longer term, larger values of γ correspond to increased dispersion, as expected.
Footnotes
¶For example, a sum of quantum random variables (see below), each of which has the same probability distribution as a classical random variable, and which equally have pairwise vanishing covariances, will generically have more extreme deviations (e.g., have higher even moments beyond the second) than the sum of the corresponding classical variables.
References
1. von Neumann J. Sbornik Ns. 1936;1:415–484.
2. Keynes J M. The General Theory of Employment, Interest, and Money. New York: Harcourt Brace; 1936.
3. Soros G. The Alchemy of Finance. New York: Simon & Schuster; 1987.
4. Grossman S J. The Informational Role of Prices. Cambridge, MA: MIT Press; 1989.
5. Shiller R J. Market Volatility. Cambridge, MA: MIT Press; 1989.
6. DeLong J, Shleifer A, Summers L H, Walddmann R J. J Finance. 1989;44:681–696.
7. Grossman S J, Stiglitz J E. Am Econ Rev. 1976;77:246–253.
8. Lo A W, MacKinlay A C. Rev Fin Stud. 1988;1:41–66.
9. Lo A W, Wang J. J Finance. 1995;50:87–129.
10. Poterba J M, Summers L H. J Finan Econ. 1988;22:27–60.
11. Black F, Scholes M. J Political Econ. 1973;3:637–654.
12. Merton R C. Bell J Econ Man Sci. 1973;4:141–183.
13. Ito K. Mem Am Math Soc. 1951;4:1–51.
14. Segal I E. Trans Am Math Soc. 1956;18:160–175.
15. Segal I E. Illinois J Math. 1962;6:500–523.
16. Kakutani S. Proc Natl Acad Sci USA. 1950;36:319–323. [PMC free article] [PubMed]
17. Doob J L. Stochastic Processes. New York: Wiley; 1965.
18. Hobson E W. The Theory of Functions of a Real Variable. Vol. 1. Cambridge, MA: Cambridge Univ. Press; 1927.
19. Arveson W. CBMS Regional Conference No. 55. Providence, RI: Am. Math. Soc.; 1983. pp. 29–40.
20. Duffie D. J Econ Theory. 1987;46:194–204.
Articles from Proceedings of the National Academy of Sciences of the United
No comments:
Post a Comment