把质量定义为“力与加速度之比”，会发现这个比值和力与速度的方向有关。于是就出现了“横质量”、“纵质量”的概念。Pauli的《相对论》中就出现了这样的名词。而Landau的《经典场论》中只是提了一句：the ratio of force to acceleration is different in the two case.
如果把质量用p = mv定义，即m是联系p和v的一个系数，（p、v是三维动量和三维速度，）这时候m就和v与a的方向无关，而仅与v的大小有关。这就是常说到的动质量。
更进一步，如果用四维的观点看待问题，p = mu（p、u分别是四维动量和四维速度，）这时候m和u的大小也无关，是一个不变量，从而能反映质点的内禀属性。现代物理说的“质量”指的往往是这个不变量。
一个带电的物体比一个没有带电的物体更难加速。因此静电能量表现成某种电磁质量，增加了物体的机械质量
狹義相對論中的質量[编辑]
维基百科，自由的百科全书
相对论性质量这一名词也被使用，而这是一个物体所具有的总共能量。物体的相对论性质量包括了它所具有的动能，因此取决于观察者所处于的参考系。
目录
[隐藏]用词[编辑]
如果一个盒子装有许多粒子，它的重量会随着这些粒子的速率的增加而增加。盒子裡的任何能量被加入盒子的质量中，因此这个盒子的质量受到这些粒子的相对运动的影响。然而，如果这整个盒子在运动，那么这盒子所具有的动能是不是应该包括在物体的质量当中呢？不变质量不包括盒子的动能，而相对论性质量则包括了盒子的动能。相对论性质量和静质量都是物理学中的传统概念，但相对论性质量只是总共能量的多余的名称。一个系统只有在静止时其质量才有可能被测量，但当物体静止时，物体的相对论性质量就是物体的静质量。
物体的不变质量是在一个特定参考系中它所具有的总共能量，而在这个参考系中，该物体是静止的。这也是不变质量也被称作静质量的缘故。这个特定的参考系也被称作动量的質心系。質心系被定义成系统的总动量为零时所处于的参考系。对于一个合成的物体（由许多更小的物体组成，这些物体可能在运动）和一组没有结合在一起的物体，只要总共的动量是零，相对论性质量便与不变质量相同。
如果一个物体以光速运动，它在任何参考系中都不会静止。当观察者朝着与这个物体运动的方向加速，该物体所具有的能量会越来越少。因此，我们可以推测这个物体的静质量是零，而这个物体所具有的质量仅是相对论性质量，一个取决于观察者的质量。
相對論性質量的概念[编辑]
早期的发展：横向与纵向质量[编辑]
约瑟夫·汤姆孙在1881年[1] 承认一个带电的物体比一个没有带电的物体更难加速。因此静电能量表现成某种电磁质量，增加了物体的机械质量。之后威廉·维恩 （1900）[2]和 Max Abraham （1902）[3] 认为一个物体的总共质量与它的电磁质量相同。因为电磁质量取决于电磁能量，维恩所提出的质能关系是
。George Frederick Charles Searle 和汤姆孙也指出，电磁质量随着物体的速度而增加。亨德里克·洛伦兹在他的洛伦兹以太理论的框架中承认这个说法。他将质量定义成所用力与加速度的比值而不是动量与速度的比值，因此他必须区分横向质量（
）（当物体运动的方向与加速度相同或相反）和纵向质量（
）（当物体运动的方向与加速度垂直）。只有当加速度与物体运动的方向垂直时，洛伦兹的质量才会等于现在被称作相对论性质量的质量。（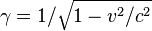
是洛伦兹因子，v是物体与以太的相对速度，c是光速）。因此，根据这一理论没有物体可以到达光速，因为物体的质量将趋于无限大。 [4] [5]而对于一个具有非零静质量的粒子在x方向运动时所受到的作用力和加速度的准确表达是：
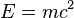的论文中（1905），m所代表的是现在认为的静质量。[8] 一些人后来声称他不喜欢相对论性质量的想法。 [9]现代相对论的概念[编辑]
在狭义相对论中，就像洛伦兹以太理论，一个静质量非零的物体无法以光速运动。当物体趋近于光速时，它的能量和动量将无限制的增加。横向质量和纵向质量被相对论性质量的概念取代。Richard C. Tolman 在1912年表示m0(1 - v2/c2)-1/2最适合用来表示运动物体的质量。[10]
在1934年，Tolman也定义相对论性质量为：[11]
对于以低于光速运动的粒子，即具有非零的静质量的粒子，这方程式变成
将等于1。当相对速度趋近光速时，将趋近无限大。在动量的方程式中
牛顿第二定律以
的形式表达仍然正确。但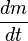
并不是零，因为相对论性质量是速率的函数，因此牛顿第二定律不能以
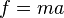来表示。一个系统的质量[编辑]
一个系统的静质量并不等于组成这一系统的所有物体的静质量的和，除非在这一系统中的所有物体在質心系是静止的而不具有其它形式的能量（如场能）。一个系统所具有的静质量等于它在質心系所具有的能量（包括场能）。相對論能量-動量方程式[编辑]
上述E和p的相對論表示式可以轉寫成基礎的「相對論能量-動量方程式」：
考慮一個靜止的物體，上面第一條方程式中的動量p為零，我們得到：
這裡的E實際上等同於前面段落中的相對論性能量方程式，而那條能量方程式和相對論性質量方程式只差了一個因子c2。因此「相對論性質量本質上等於總能量」—，但是量值與單位有些差別。 當採用c = 1的單位(稱作自然單位系統)時，能量-動量方程式即簡化為：
狭义相对论中的质量守恒定律[编辑]
能量是可加的守恒的量，但静质量不是。这意味着当我们可以确认一系统是封闭的，该系统的静质量和动量才会守恒。相对论性质量本质上就是能量，因此能量守恒定律就是相对论性质量守恒定律。一个光子本身没有静质量。一个具有静质量的粒子可以衰变成光子，然而这个由光子组成的系统却具有静质量，因此一个系统的静质量并不等于组成它的粒子的静质量的和。无论在衰变前后，这个封闭的系统的静质量都是守恒的。
一个系统如果保持相同的静质量，它必须是封闭的，以致没有能量（可能是热或辐射）可以逃离该系统。外力可以改变该系统的动量和能量，但该系统的动量和能量的改变可以维持静质量不变。当某些反应将组成该系统的某些粒子的静质量转换成光能或热能，只要这些光能或热能无法从该系统逃离，该系统的静质量便不会改变。只有在这些能量被释放到该系统周围的环境，该系统才会失去静质量。
争议[编辑]
根据Lev Okun的说法，[12]. 爱因斯坦本人一直用m来表示不变质量，而不用m来表示其它任何质量。Okun和他的跟随者拒绝相对论性质量的概念。Arnold B. Arons否定教导相对论性质量的概念：[13]多年来人们传统上通过相对论性质量的推导来进入动力学的讨论。质量与速度的关系可能在主流课本中仍有提及。然而，最近，越来越多人承认相对论性质量是一个麻烦和令人生疑的概念。[看，例如, Okun (1989).]合理和严格途径至相对论动力学是直接发展可以保证在所有参考系中动量守恒的动量：另一方面，T. R. Sandin 写道：[14]
而不是通过相对论性质量。
相对论性质量的概念为对狭义相对论初学者的教导带来了一致性和简单。例如，必须注意的是质量和速度的关系例如
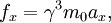
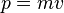
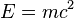
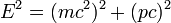
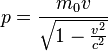
No comments:
Post a Comment