显示全部
-
在每一个可能的世界中，pi 都是这个值。
为什么？
下面我们要区分两种可能性，一种是逻辑可能，一种是物理可能。
逻辑可能的事情比物理可能的事情要多，相对地，逻辑不可能的事情比物理不可能的事情要少。
举一个例子，在我们这个世界上，超过光速是物理不可能的事情。但这并非逻辑不可能。
那么，什么是逻辑不可能的呢？比如说一只熊，是白色的并且不是白色的。同时，你这句话中的两个白色是相同的概念。那么这句话就是逻辑不可能的。（有人认为这个地方有一种逻辑沙文主义，即，认为只有西方亚里士多德逻辑才是正确的逻辑，但是真的是这样吗？「且」、「非」、「或」这些语言的意义由其用法决定，如果有人告诉你，某个文明认为「p 且非 p」是可以接受的，难道你的第一反应不会是「翻译错了」吗？）
类似地，方的圆、弯的直、黑的白这些概念都是逻辑不可能的。前提是你在使用这些概念的时候，确实认为这两者是日常语境下的相互对立的概念。
「如果在某个宇宙中」这个假设，在什么情况下可以使用呢？针对逻辑可能，但是物理不可能的事件的时候。
首先，如果一个事件是逻辑不可能的，那么在任何一个可能世界中，它都是不会发生。或者说，这个概念本身所指的对象是无法想象的，比如说方的圆。自然地，世界上不存在逻辑不可能但是物理可能的事情。
其次，如果一个事件是物理可能的，那么就没有必要画蛇添足地加上一个「如果在某个宇宙中」，直接问是否可能就好了。
综上。问题不成立。
你可能会问，那如果在某个可能世界中，人们不把现在的圆称为圆，而把另一种图形称为圆，那该怎么办？要注意，我们关注的不是特殊的语词，我们关注的是这个抽象的概念。它的名称是什么不重要。所以在每个可能世界中，如果圆不是一个欧式空间中的平面上到定点距离为定值的所有点的集合，那么讨论的 pi 就不再是我们所讨论的那个概念。
另外补充一点，没记错的话，用同样的速度绕太阳一周，和沿着直径穿过太阳所花的时间比是小于 pi 的……因为加上了引力场的宇宙不是欧式空间。
关于可能和不可能的分歧，其实已经无关于物理了，而主要集中在数学模型上。
的确，如果单纯的圆周和直之比，那么在非平直的空间中，这个值的确可以不等于 pi，但是，作为常数的圆周率，在定义的时候有一系列的条件。第一个条件就是要是常数。如果可以证明非欧空间中的圆周率不是常数的话或许问题就解决了？
当然，更简单的方式就是认定了圆周率就是这样的东西。就像是在任何一个可能世界中 1+1=2 那样。
补充一下，我们还可以在逻辑可能性和物理可能性之间找到一个中间者：本体论意义上的（ontological）可能性。这种可能性是克里普克提出来的，事实上他提出的是本体论意义上的必然性。他用了 Frege 的一个经典例子，「晨星是暮星」，在这里，晨星和暮星都是专名，进而他指出，如果我们保证「晨星」、「暮星」这两个专名的所指不变，那么「晨星必然等同于暮星」，如果在某个可能世界中，晨星和暮星是两颗不同的星，那么只能说明在那个可能世界中，人们使用「晨星」和「暮星」的规则与我们的规则不同。因此他宣称自己找到了一个本体论意义上必然的后天命题。不过由于本体论意义上的必然性太难理解，所以我们只能确定它比逻辑必然性要弱，而比物理必然性要强。虽然我试图主张本体论意义上的必然性等价于逻辑必然性，但是暂时没有找到合适的理由。
有人可能要开始胡搅蛮缠了：为什么就一定不能是非欧空间呢？
请问你希望 pi 是一个常量还是一个变量？如果你认为 pi 是一个变量，那么讨论本身就是没有意义的，一个变量爱取什么值取什么值，如果你认为 pi 是一个常量，请问一个常量能取两个值么？pi 是圆周率，没错，但是别忘了这个地方是有默认语境的，并且 pi 已经可以通过别的无关于几何的方式重新定义。难道我说 1+1=2，你都要反驳我说：「胡扯！在只有两个元的加法群中 1+1=0！」？
假设有一个文明中的空间结构和我们不同，这时我们问，请问这个文明中的人能计算以下连分数么？
（注意，这个地方作为反驳的依据，不能使用诸如
等包含了考虑了面积这个概念的公式）
能，那好，他们在某些方面上来说有着和我们相同的数学能力。
那么我们的问题是，这个连分数是一个常数，而对应文明中的圆周率也是一个常数，我们在翻译的时候会把何者称为 pi 呢？显然是前者，因为对于后者，我们有别的名称来进行描述。
注意，如果两个文明分别只发展了欧氏几何和非欧几何，那么这两个文明的几何是不可通约的。他们在用词的时候都会吵起来，因为这两个几何的六条公理（前四条相同）放在一起是一个不一致的系统。在这种情况下，翻译是无法进行的，就像是说，一个民族从未见过雨雪，只见过冰雹，另一个民族只见过雨，这种情况下，我们能认为他们语言中对应的表示下冰雹和下雨的词是相同的词么？显然不能。而如果一个民族只见过冰雹，而另一个民族见过雨、雪、冰雹，那个更为高级的民族有必要认为自己的语言中的「雨」对应的是对方语言中的「冰雹」么？也没有必要。至于这个地方，你说，「但是但是，如果我们像那样发展文明，的确有可能用『雨』来表示冰雹啊！」废话，符号的选用是任意的啊！
顺便说一下对于几何概念的两种理解。对于几何概念，比如说点、线、面，一种理解是，这些几何概念的定义仅由最为初始的定义决定；另一种理解是，要理解「点」、「线」、「面」，我们不仅要理解这些概念本身，还需要同时知道对应的公理，才算是理解了这个概念。也即，公理通过隐定义的方式，规定了这些词的使用方式。
这个划分有什么意义呢？如果是基于前者，那么欧氏几何和非欧几何中的词的含义是相同的，而基于后者，它们的含义从一开始就是不同的。
- 显示全部
在每一个可能的世界中，pi 都是这个值。
为什么？
下面我们要区分两种可能性，一种是逻辑可能，一种是物理可能。
逻辑可能的事情比物理可能的事情要多，相对地，逻辑不可能的事情比物理不可能的事情要少。
举一个例子，在我们这个世界上，超过光速是物理不可能的事情。但这并非逻辑不可能。
那么，什么是逻辑不可能的呢？比如说一只熊，是白色的并且不是白色的。同时，你这句话中的两个白色是相同的概念。那么这句话就是逻辑不可能的。（有人认为这个地方有一种逻辑沙文主义，即，认为只有西方亚里士多德逻辑才是正确的逻辑，但是真的是这样吗？「且」、「非」、「或」这些语言的意义由其用法决定，如果有人告诉你，某个文明认为「p 且非 p」是可以接受的，难道你的第一反应不会是「翻译错了」吗？）
类似地，方的圆、弯的直、黑的白这些概念都是逻辑不可能的。前提是你在使用这些概念的时候，确实认为这两者是日常语境下的相互对立的概念。
「如果在某个宇宙中」这个假设，在什么情况下可以使用呢？针对逻辑可能，但是物理不可能的事件的时候。
首先，如果一个事件是逻辑不可能的，那么在任何一个可能世界中，它都是不会发生。或者说，这个概念本身所指的对象是无法想象的，比如说方的圆。自然地，世界上不存在逻辑不可能但是物理可能的事情。
其次，如果一个事件是物理可能的，那么就没有必要画蛇添足地加上一个「如果在某个宇宙中」，直接问是否可能就好了。
综上。问题不成立。
你可能会问，那如果在某个可能世界中，人们不把现在的圆称为圆，而把另一种图形称为圆，那该怎么办？要注意，我们关注的不是特殊的语词，我们关注的是这个抽象的概念。它的名称是什么不重要。所以在每个可能世界中，如果圆不是一个欧式空间中的平面上到定点距离为定值的所有点的集合，那么讨论的 pi 就不再是我们所讨论的那个概念。
另外补充一点，没记错的话，用同样的速度绕太阳一周，和沿着直径穿过太阳所花的时间比是小于 pi 的……因为加上了引力场的宇宙不是欧式空间。
关于可能和不可能的分歧，其实已经无关于物理了，而主要集中在数学模型上。
的确，如果单纯的圆周和直之比，那么在非平直的空间中，这个值的确可以不等于 pi，但是，作为常数的圆周率，在定义的时候有一系列的条件。第一个条件就是要是常数。如果可以证明非欧空间中的圆周率不是常数的话或许问题就解决了？
当然，更简单的方式就是认定了圆周率就是这样的东西。就像是在任何一个可能世界中 1+1=2 那样。
补充一下，我们还可以在逻辑可能性和物理可能性之间找到一个中间者：本体论意义上的（ontological）可能性。这种可能性是克里普克提出来的，事实上他提出的是本体论意义上的必然性。他用了 Frege 的一个经典例子，「晨星是暮星」，在这里，晨星和暮星都是专名，进而他指出，如果我们保证「晨星」、「暮星」这两个专名的所指不变，那么「晨星必然等同于暮星」，如果在某个可能世界中，晨星和暮星是两颗不同的星，那么只能说明在那个可能世界中，人们使用「晨星」和「暮星」的规则与我们的规则不同。因此他宣称自己找到了一个本体论意义上必然的后天命题。不过由于本体论意义上的必然性太难理解，所以我们只能确定它比逻辑必然性要弱，而比物理必然性要强。虽然我试图主张本体论意义上的必然性等价于逻辑必然性，但是暂时没有找到合适的理由。
有人可能要开始胡搅蛮缠了：为什么就一定不能是非欧空间呢？
请问你希望 pi 是一个常量还是一个变量？如果你认为 pi 是一个变量，那么讨论本身就是没有意义的，一个变量爱取什么值取什么值，如果你认为 pi 是一个常量，请问一个常量能取两个值么？pi 是圆周率，没错，但是别忘了这个地方是有默认语境的，并且 pi 已经可以通过别的无关于几何的方式重新定义。难道我说 1+1=2，你都要反驳我说：「胡扯！在只有两个元的加法群中 1+1=0！」？
假设有一个文明中的空间结构和我们不同，这时我们问，请问这个文明中的人能计算以下连分数么？
能，那好，他们在某些方面上来说有着和我们相同的数学能力。
那么我们的问题是，这个连分数是一个常数，而对应文明中的圆周率也是一个常数，我们在翻译的时候会把何者称为 pi 呢？显然是前者，因为对于后者，我们有别的名称来进行描述。
注意，如果两个文明分别只发展了欧氏几何和非欧几何，那么这两个文明的几何是不可通约的。他们在用词的时候都会吵起来，因为这两个几何的六条公理（前四条相同）放在一起是一个不一致的系统。在这种情况下，翻译是无法进行的，就像是说，一个民族从未见过雨雪，只见过冰雹，另一个民族只见过雨，这种情况下，我们能认为他们语言中对应的表示下冰雹和下雨的词是相同的词么？显然不能。而如果一个民族只见过冰雹，而另一个民族见过雨、雪、冰雹，那个更为高级的民族有必要认为自己的语言中的「雨」对应的是对方语言中的「冰雹」么？也没有必要。至于这个地方，你说，「但是但是，如果我们像那样发展文明，的确有可能用『雨』来表示冰雹啊！」废话，符号的选用是任意的啊！
顺便说一下对于几何概念的两种理解。对于几何概念，比如说点、线、面，一种理解是，这些几何概念的定义仅由最为初始的定义决定；另一种理解是，要理解「点」、「线」、「面」，我们不仅要理解这些概念本身，还需要同时知道对应的公理，才算是理解了这个概念。也即，公理通过隐定义的方式，规定了这些词的使用方式。
这个划分有什么意义呢？如果是基于前者，那么欧氏几何和非欧几何中的词的含义是相同的，而基于后者，它们的含义从一开始就是不同的。
- 显示全部
首先定义下，圆为空间中到某一点的距离为R的所有点的集合。在欧氏空间中，毫无疑问不可能出现PI非3.14的情况。但是非欧空间就可以。
为了让大家有亲切感，我们来找一个大家最熟悉的非欧平面：地球表面。
地球表面可以看做一个黎曼几何平面，在这个平面上，没有固定的PI值。
当R无穷小的时候，PI会无限接近3.14，而当R大到地球周长1/4的时候，PI恰巧为2。
R继续增大，PI值会越变越小，当R恰好等于地球周长1/2的时候，PI变为0。
为了让大家有亲切感，我们来找一个大家最熟悉的非欧平面：地球表面。
地球表面可以看做一个黎曼几何平面，在这个平面上，没有固定的PI值。
当R无穷小的时候，PI会无限接近3.14，而当R大到地球周长1/4的时候，PI恰巧为2。
R继续增大，PI值会越变越小，当R恰好等于地球周长1/2的时候，PI变为0。
Pi可以纯代数的定义出来，这样，就无关现实宇宙的几何构型了。
某个数学八卦提到，德国一位牛数学家（代数学家）写了一本代数教科书，三角函数就是完全用级数和定义的，与几何没有任何关系，然后同样可以推导出所有的三角函数关系。（好象是鲁丁）
某个数学八卦提到，德国一位牛数学家（代数学家）写了一本代数教科书，三角函数就是完全用级数和定义的，与几何没有任何关系，然后同样可以推导出所有的三角函数关系。（好象是鲁丁）
我回家想了个很简单的办法，证明在我们目前所处的宇宙的所有不含奇点的部分，pi永远是3.1415926...，不会因为黎曼张量或者它的缩并---里奇张量不为0而成为不是这个常数。
理由很简单，爱因斯坦场方程：
R_uv-1/2*R*g_uv+Λ*g_uv=κ*T_uv
是描述我们所处的宇宙，其中包括了里奇张量和宇宙学常数。并且，其中常数k指的是：8Gπ/c^4
你们看，这个场方程就是含π的，并且对这个常量没有做出和3.1415926...不同的说明。
所以，依靠这个很懒的证明，我们只需要考虑一个和我们完全不一致的宇宙就可以了。或者只考虑我们宇宙的某些特殊奇点即可。那里有可能存在不是这个值的π。
理由很简单，爱因斯坦场方程：
R_uv-1/2*R*g_uv+Λ*g_uv=κ*T_uv
是描述我们所处的宇宙，其中包括了里奇张量和宇宙学常数。并且，其中常数k指的是：8Gπ/c^4
你们看，这个场方程就是含π的，并且对这个常量没有做出和3.1415926...不同的说明。
所以，依靠这个很懒的证明，我们只需要考虑一个和我们完全不一致的宇宙就可以了。或者只考虑我们宇宙的某些特殊奇点即可。那里有可能存在不是这个值的π。
反对@罗心澄的答案。
首先，罗狭义化了圆的定义，他说
其次，罗割裂了圆周率和π的定义。当我在他的答案里评论是他是这么回答的
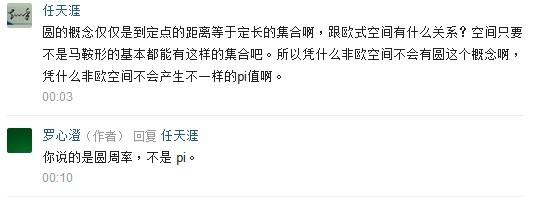圆周率不是π.........
别这样好吗
维基是这么说π的 http://en.wikipedia.org/wiki/Pi
所以把圆周率和π割裂开来，或者说圆周率可以不是常量而π必须是这种说法，或认为别的曲率空间圆周率可以不等于3.14...这个无理数而π还必须是这个无理数的说法，就是耍流氓了，毫无疑问。 显示全部
首先，罗狭义化了圆的定义，他说
在每个可能世界中，如果圆不是一个欧式空间中的平面上到定点距离为定值的所有点的集合，那么讨论的 pi 就不再是我们所讨论的那个概念。事实上数学上并没有规定圆必须是欧氏空间的。只要到定点举例是常数的集合，那就是圆，至于是在欧氏空间还是在非欧空间，毫无问题好吗。
其次，罗割裂了圆周率和π的定义。当我在他的答案里评论是他是这么回答的
圆周率不是π.........别这样好吗
维基是这么说π的 http://en.wikipedia.org/wiki/Pi
The symbol used by mathematicians to represent the ratio of a circle's circumference to its diameter is the Greek letter π. That letter (and therefore the number π itself) can be denoted by the Latin word pi.中文维基是这么说圆周率的，圓周率
[2]In English, π is pronounced as "pie" ( /paɪ/, /ˈpaɪ/).[3]The lower-case letter π (or π in sans-serif font) is not to be confused with the capital letter Π, which denotes a product of a sequence.Definition
The circumference of a circle is slightly more than three times as long as its diameter. The exact ratio is called π.
π is commonly defined as the ratio of a circle's circumferenceC to its diameterd:
[4]
圆周率，一般以π来表示，是一个在数学及物理学普遍存在的数学常数，是精确计算圆周长、圆面积、球体积等几何量的关键值，其定义为圆的周长与直径的比值。也等于圆的面积与半径平方的比值。
所以把圆周率和π割裂开来，或者说圆周率可以不是常量而π必须是这种说法，或认为别的曲率空间圆周率可以不等于3.14...这个无理数而π还必须是这个无理数的说法，就是耍流氓了，毫无疑问。 显示全部
知乎用户，The truth is what it is,not what you see
收起
其实这个问题可以类比为：
如果一个正方形的对角线和边的比不是√2，那这世界会怎样。
问题是如果对角线和边的比不是√2，那么这个图形还是正方形吗？
这个用勾股定理应该很容易证明。
你也可以这么理解，√2这个数字定义了正方形。
那么也可以等同理解为π其实也定义了圆。
那么既然定义都变化了，那么这个还是圆吗？
--------------------------------------------------------
当然，如果不考虑这么多问题，单纯的思考题主的问题。
π能给人带来最直观的感受应该就是周长和面积了。
那么如果π变大了，那么同半径的圆周长和面积就要变大了。。。
是不是本来题主一顿饭要吃两张饼，现在一张就够了。。。。
题主家的桶装卫生纸可能要用好久、、、、、、、、
以及各种奇怪的现象。。。。
如果一个正方形的对角线和边的比不是√2，那这世界会怎样。
问题是如果对角线和边的比不是√2，那么这个图形还是正方形吗？
这个用勾股定理应该很容易证明。
你也可以这么理解，√2这个数字定义了正方形。
那么也可以等同理解为π其实也定义了圆。
那么既然定义都变化了，那么这个还是圆吗？
--------------------------------------------------------
当然，如果不考虑这么多问题，单纯的思考题主的问题。
π能给人带来最直观的感受应该就是周长和面积了。
那么如果π变大了，那么同半径的圆周长和面积就要变大了。。。
是不是本来题主一顿饭要吃两张饼，现在一张就够了。。。。
题主家的桶装卫生纸可能要用好久、、、、、、、、
以及各种奇怪的现象。。。。
知乎用户，个人一句话介绍
收起
排名第一的回答显然是狡辩(玩概念游戏)。我想题主的问题用数学语言描述的话可能是下面的内容：
如果定义 圆周率函数r(d)=C/d，其中C是圆周长，d是直径。则r的极大值或极小值必有一个等于π。
上面这个问题我解答不了。不过我在网上看到一段话：
整体地说,单连通的完备常曲率空间只能是下列三种：球面、欧氏空间和双曲空间。
欧式空间里r是常数=π，球空间和双曲空间里r(0)=π。所以如果能够定义r(d)则题主的问题应该是不成立的
如果定义 圆周率函数r(d)=C/d，其中C是圆周长，d是直径。则r的极大值或极小值必有一个等于π。
上面这个问题我解答不了。不过我在网上看到一段话：
整体地说,单连通的完备常曲率空间只能是下列三种：球面、欧氏空间和双曲空间。
欧式空间里r是常数=π，球空间和双曲空间里r(0)=π。所以如果能够定义r(d)则题主的问题应该是不成立的
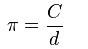
果然应该就是完全不明白呀。
2、非剪切扭转的对称群度规下，不同黎曼曲率下的圆周与半径比到底会不会变化？我好像没有找到明确答案？
谢谢～～～