能谱,判断其存则用热力学能量
我长期的思索带来了一个信念,超导有生和存两个环节。判断其生是用量子力学
能谱,判断其存则用热力学能量。
这个想法可用一个比喻来让不做超导的网友明白。量子力学与热力学在超导体上
的理论矛盾是微观解释与宏观解释的矛盾,就象一个孩子的生和养。生孩子从本
质上来说是两人的事,比之于微观的;把孩子养大和孩子长大后的表现是社会性
的,比之于宏观的。超导能不能在一个导体内生成是微观的,受量子力学控制;
生成超导的机制有了以后能不能实现并被观察到是宏观的,受热力学控制
我长期的思索带来了一个信念,超导有生和存两个环节。判断其生是用量子力学
能谱,判断其存则用热力学能量。
这个想法可用一个比喻来让不做超导的网友明白。量子力学与热力学在超导体上
的理论矛盾是微观解释与宏观解释的矛盾,就象一个孩子的生和养。生孩子从本
质上来说是两人的事,比之于微观的;把孩子养大和孩子长大后的表现是社会性
的,比之于宏观的。超导能不能在一个导体内生成是微观的,受量子力学控制;
生成超导的机制有了以后能不能实现并被观察到是宏观的,受热力学控制。
这个想法今天讲来简明,我当时却是混混巫巫的折腾,直到我锻出宝刀,打通
了超导在微观与宏观的通路为止。有了这个观点,回看各家超导理论,六经注
我,再无窒碍。我只看一个理论怎样描述超导的生,怎样描述超导的存,是否
能有生和存的标准。
这把屠龙宝刀是在超晶格的情况下先打造出来的,形式还要复杂一点,但是写文
章时我却为难了。屠龙宝刀虽利,但只能在比武场里助我,能不能上比武场又是
另外一层障碍。这一篇文章要推出从量子力学到电动力学到热力学的三部曲;
要改变κ的定义;要给超晶格中新的涡旋点阵;要推广阿布利科索夫的理论。
有这几个内容,无论什么地方审稿者对不上眼,都可能拒稿。
"朗道的超导理论到1950年推广成了金茨伯格-朗道理论,这个理论的具体形式大概
每本超导理论的书上都有。此理论的要点是把“序参量”改进成了一个“波函
数”。在上个帖子里,我介绍了朗道理论ΔF= -α|Ψ|^2+β|Ψ|^4,在这个形式里,
这个“序参量”Ψ,是与空间坐标无关的数,而在金茨伯格-朗道理论中这个“序
参量”被写成ψ(x),这里的x是指(x,y,z)三个空间坐标,就以记号而论,网友们不
妨把它看成“波函数”。这一个改进非同小可,因为ψ(x)如果在空间有变化(嘻嘻,
这是一定的,不然改个bird啊),那么就要在自由能中加格外的能量来解释这个空
间变化。实际上这正是金茨伯格和朗道要的,这个额外的能量一加,就有了微分
算符的出现,於是,对金茨伯格-朗道自由能做变分就出来了金茨伯格-朗道微分
方程。方程一共有两个,第二个是常见的磁场-电流密度方程,而第一个是著名的
金茨伯格-朗道非线性微分方程,如果把非线性项丢掉,这个方程与量子力学波动
方程有几乎一模一样的形式,差别只在两个常数的意义上,一个是质量m*,什么东
西的质量?一个是电荷e*,什么东西的电荷?我们可以暂时接受一个结论,
m*=2m,e*=2e,是两倍的电子质量和两倍的电子电荷。"
上一讲中已经讲到小C提出的电子配对思想,也就是费米面上两个电子由于微弱的吸引力而配成对。
这是个很好的出发点,老B 就死死地盯住这个核心,让小C小S 寻找系统的最小能量解。
小S 鬼使神差地想到,超导基态应该是个电子对形成的相干态。这大概就是灵感。
相干态是个很神奇的量子态,粒子数不定,但具有最小的位相涨落。很多玻色子凝聚相都处于相干态,比如激光。
电子是费米子,想处于相干态就需要做点手脚。
小S 发现,按照小C的主意把电子全都配成对对儿,就可以写出一个相干态来。
大量的非超导电子集体就像一个海洋,时而蹦几个出来成为超导电子或者反回来,形成了粒子数不固定的相干态。
小S以这个相干态为基态,对能量求极小值,就得到了一个漂亮的超导解。
另一条路是对吸引相互作用做平均场近似。这也是不得已的办法,谁叫人类至今也没办法求解4条腿(4个产生湮灭算符)的多体问题呢。
很神奇的是,这样近似之后直接求解,竟然跟小S 的相干态解完全一样。
于是,BCS的超导解就这样定下来了。
BCS之美(二):B, C, S这伙人的故事
http://blog.sciencenet.cn/blog-222979-583103.html 此文来自科学网李铭博客
上一篇:[转载]爱国不需要理由吗?
下一篇:在黄秀清取得量子八卦重大突破庆功晚宴上的讲话
|||
本来不想干这种吃力不讨好的事,看了会仟老师的超导博文,感到意犹未尽,再做点补充。
话说老B (就是巴丁,比另两个老了10几20岁),可不是个等闲之辈。
他多次跳槽,40年代末正好是贝尔电话公司的电子器件方面的研究人员,他和同事一起发明了半导体三极管。
他因此和几个人分享了1956年的诺贝尔物理学奖,够牛B了吧。
但是,他还嫌不够。
由于他早年具有固体理论方面的研究基础,他了解了小C(库伯)的配对思想,突然对超导发生了兴趣。
他就召集了当时小有成就的小C 和聪明的小S(西里夫)来研究超导理论。
老B应该只是做点指手画脚的工作,小C和小S 是具体的理论创造者。
上一讲中已经讲到小C提出的电子配对思想,也就是费米面上两个电子由于微弱的吸引力而配成对。
这是个很好的出发点,老B 就死死地盯住这个核心,让小C小S 寻找系统的最小能量解。
小S 鬼使神差地想到,超导基态应该是个电子对形成的相干态。这大概就是灵感。
相干态是个很神奇的量子态,粒子数不定,但具有最小的位相涨落。很多玻色子凝聚相都处于相干态,比如激光。
电子是费米子,想处于相干态就需要做点手脚。
小S 发现,按照小C的主意把电子全都配成对对儿,就可以写出一个相干态来。
大量的非超导电子集体就像一个海洋,时而蹦几个出来成为超导电子或者反回来,形成了粒子数不固定的相干态。
小S以这个相干态为基态,对能量求极小值,就得到了一个漂亮的超导解。
另一条路是对吸引相互作用做平均场近似。这也是不得已的办法,谁叫人类至今也没办法求解4条腿(4个产生湮灭算符)的多体问题呢。
很神奇的是,这样近似之后直接求解,竟然跟小S 的相干态解完全一样。
于是,BCS的超导解就这样定下来了。
这个BCS超导解漂亮在哪里? 首先,刚才讲的相干态解和平均场近似解惊人一致,条条道路通罗马,不能全当是巧合。
第二,这样一个配对机制,有一个最小的激发能。小于这个激发能,不能有激发,电阻也就不能存在。没有哪个其他的模型能如此完美解释超导性。这个解释跟朗道的超流二级相变理论有点相似。
第三,这个BCS模型还同时解释了超导体的完全抗磁性。磁场进不去超导体。
第四,居然有人用BCS模型证明出了超导的金兹堡-朗道二级相变理论的序参量。
第五,杨振宁也来凑了个热闹,发现BCS超导态具有非对角长程序。这个东西当时惊爆了好些人的眼球,讲的是一对电子和很远(无穷远)的一对电子有关联。它后来成了一个超导的判据。
第六,就算BCS模型不适用于高温超导,但BCS的配对思想仍然几乎是所有高温超导模型的出发点。
所以,BCS你不服不行。BCS的确有丑的一面,没有丑就没有美。且听下回分解。
http://blog.sciencenet.cn/blog-222979-583103.html 此文来自科学网李铭博客
上一篇:[转载]爱国不需要理由吗?
下一篇:在黄秀清取得量子八卦重大突破庆功晚宴上的讲话
BCS之美(三):电子空穴组合
|||
BCS的关键是考虑了电子和空穴的耦合, α k =u k C k +v k C † −k
. 为了简化,这里的 k 还带着上自旋指标,-k 带着下自旋指标。由于产生一个空穴等于湮灭一个动量相反自旋相反的电子,我们可以把其中的C † −k
写成空穴算符 D k
。这样 α k =u k C k +v k D k
,我们就能很明显地看到是电子和空穴的组合。这个组合称为准粒子。
固体中电子和空穴甚至可以像氢原子中的质子和电子一样结合起来成为一对儿,就是激子。在一些半导体材料中可以观察到激子能级。但是 BCS的电子空穴组合不是激子,它不是一对儿。它既不是一个电子也不是一个空穴,而是一部分电子,一部分空穴。这是一个奇特的组合,称为准粒子。它的电荷数是个小于1的小数。这一点好像从来没人讲过。我个人觉得,这正是BCS的丑的一面。但是,瑕不掩瑜,任何事物都不会十全十美。
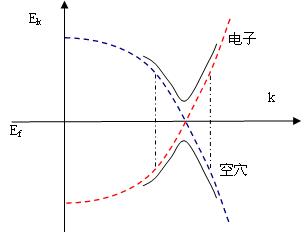
电子和空穴的是怎么组合起来的?见下图,图中红色虚线是自由电子的能谱,蓝色虚线是自由空穴的能谱,它们关于费米面Ef完全对称。在两能谱相交的地方,也就是费米面附近,电子和空穴之间有显著的相互作用(吸引),从而发生组合,产生能隙。组合以后的新能谱见黑色实线。可见,新能谱(实线)和旧能谱(虚线)很相似,新能谱不过是旧能谱基础上的小小变形。如果你熟悉固体能带,这种能隙的发生就没什么奇怪的。比如晶体的两个相邻的自由电子能谱在布里渊区的边界上相交,由于相互作用而产生能隙。图中两条竖直的点划线表示相同波矢的电子和空穴的组合。组合形成的准粒子的能量为上下两条实曲线,公式为E=±E 2 k +|Δ| 2 − − − − − − − − √
。

这样一个组合的最显著的特点是,准粒子能量有一个能隙|Δ|
,即实曲线的底部与费米面的距离. 这是超导的根本原因。
这样产生的两个准粒子能带和普通的晶体能带之间有个重大的区别。普通晶体的基态总是先填充下能带,形成价带。价带不满,就导电;价带满了就绝缘。而BCS基态的这两个准粒子能带都是空的,既没有准电子,也没有准空穴。加上足够的电压,就可以产生准电子和准空穴。
库伯对在哪里?且听下回。
BCS之美(四):库伯对
|||
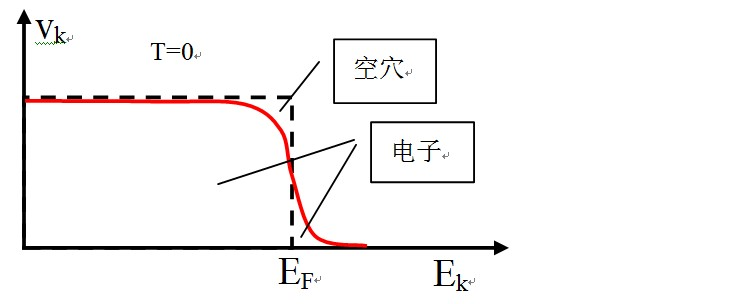
由于电子空穴组合,超导体内部电子在能量上的分布发生了变化。对于非超导材料来讲,温度为0的时候,电子填满在费米能级以下的所有能级。此时,如下图虚线所示,费米能级以上能级是空的,而费米能级以下是满的。但是,如果存在超导凝聚,在费米能级 EF附近,电子分布有一点点改变。此时,如下图红色实线所示,费米能级以上有了电子,费米能级以下有了空穴。

就是这样一个电子分布改变,导致超导体内电子发生凝聚。费米面附近的电子,也就是上图中红色曲线跨过EF附近的电子发生配对,形成动量为0的库伯对。由于它们的动量都是0,这就相当于玻色-爱因斯坦凝聚BEC。
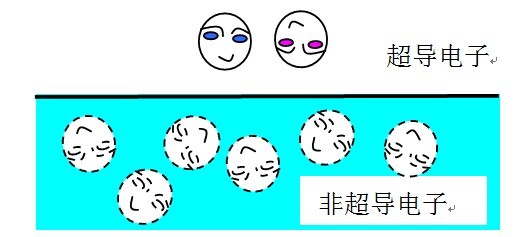
库伯对是很奇特的。一个库伯对中的两个电子并不像氢原子中的电子和质子结合在一起,而是像“潜水”一样,时而一起浮出“水面”时而一起潜入“水下”。一个库伯对可以写成 (u k +v k C † k C † −k )|0>
。其中 |v k | 2
是两个电子浮出“水面”的概率,而|u k | 2
是两个电子潜入“水面”的概率(这里的“水”指的是非超导电子)。越是靠近费米面,超导电子的潜入效果越显著。

如上图所示,库伯对中的两个电子,就像图中两哥们,在“水面”上下蹦来蹦去,而且他们步调一致。但在“水面”以下,它们就跟其他电子混在一起乱了。可见,这种配对的图像,跟很多人想象的配对是完全不同的。
超导凝聚的关键还在于,所有库伯对与共同的位相,也就是u k /v k
的位相相同。
(注:我写这个系列是个整理思路的过程。我发现,一边写还能一边有一些新想法。这是科普的好处。)
BCS之美(五):为什么没电阻
|||
现在关于BCS超导的争论,已经基本熄火,主要原因是缺氧,因为龚博主不出面。BCS理论看起来很简单,非常直观地解释了低温超导的物理机制,而且BCS对高温超导也有重要的借鉴意义,因为配对机制仍然是基础。这里我讲讲BCS怎么解释超导体的0电阻。
超导体内的电子因为库伯配对,形成一个凝聚体,产生了一个凝聚能。凝聚能可以这样理解,如果你想拆开这些配对,就要最少消耗凝聚能这么多能量。任何一种结合,都有这样一个能量的,比如H原子的一个质子和一个电子结合在一起,有个结合能13.6eV, 如果要拆开一个氢原子,也就是把它的电子敲出去,就要最少消耗13.6eV的能量。超导体中的电流要产生电阻,电能转化热,能量只能来自于凝聚体的动能。如果凝聚体的动能小于刚才讲的凝聚能,凝聚体就没法损失能量,从而产生不了热,于是没电阻。当电流密度足够大,也就是库伯对的漂移速度足够大,j=nev
,凝聚体的动能达到凝聚能,电阻就来了。这个电流就是超导体的临界电流j c
。所以,当电流密度小于j c
, 超导体就没电阻。这个解释跟朗道对超流的解释是相同的。
有超导电流的时候,整个凝聚体作为一个整体往前跑。这件事情可以反过来看问题。以凝聚体质心为参考系,晶格所有的正离子往后跑,而且速度一样。 而凝聚体还是原来那个没有电流时候的凝聚体。以晶格为参照系,情况有点复杂,因为凝聚体中的库伯对占据了费米面以下所有的动量值,有各个方向的动量。这个图像让黄秀清很纠结。其实,一个普通材料中电子的动量分布也是有各向均衡的,否则大量电子就有定向的集体运动。黄猴想不通,一个库伯对,动量相反,也就是速度相反,怎么能一起往前跑。其实,一个库伯对,并不是固定的两个电子配成的对,是大量电子的集体行为,电子不断高频碰撞,动量在随时改变,相反的动量总是存在的。
黄猴还质疑电子吸收声子形成库伯对的机制,他觉得这种声子媒介不需要时间的事情不可信。这样一种图像是现代物理学对相互作用的普遍描述,是量子场论的基本内容。比如电磁作用在量子电动力学中表现为电荷之间的光子交换,强作用在量子色动力学中是夸克之间的胶子交换,弱作用在弱电统一理论中是Z,W+,W-这些中间玻色子交换,都是不用时间的。这种描述已经取得了巨大的成就,早已成为现代物理学的基本内容。这些中间交换的媒介粒子的确是虚粒子,不满足质壳关系,所以,是不可以用仪器测量到的。它们只是一种数学描述,称为费曼图。但独立的媒介粒子可以测量到。
超导体内的电子因为库伯配对,形成一个凝聚体,产生了一个凝聚能。凝聚能可以这样理解,如果你想拆开这些配对,就要最少消耗凝聚能这么多能量。任何一种结合,都有这样一个能量的,比如H原子的一个质子和一个电子结合在一起,有个结合能13.6eV, 如果要拆开一个氢原子,也就是把它的电子敲出去,就要最少消耗13.6eV的能量。超导体中的电流要产生电阻,电能转化热,能量只能来自于凝聚体的动能。如果凝聚体的动能小于刚才讲的凝聚能,凝聚体就没法损失能量,从而产生不了热,于是没电阻。当电流密度足够大,也就是库伯对的漂移速度足够大,
有超导电流的时候,整个凝聚体作为一个整体往前跑。这件事情可以反过来看问题。以凝聚体质心为参考系,晶格所有的正离子往后跑,而且速度一样。 而凝聚体还是原来那个没有电流时候的凝聚体。以晶格为参照系,情况有点复杂,因为凝聚体中的库伯对占据了费米面以下所有的动量值,有各个方向的动量。这个图像让黄秀清很纠结。其实,一个普通材料中电子的动量分布也是有各向均衡的,否则大量电子就有定向的集体运动。黄猴想不通,一个库伯对,动量相反,也就是速度相反,怎么能一起往前跑。其实,一个库伯对,并不是固定的两个电子配成的对,是大量电子的集体行为,电子不断高频碰撞,动量在随时改变,相反的动量总是存在的。
黄猴还质疑电子吸收声子形成库伯对的机制,他觉得这种声子媒介不需要时间的事情不可信。这样一种图像是现代物理学对相互作用的普遍描述,是量子场论的基本内容。比如电磁作用在量子电动力学中表现为电荷之间的光子交换,强作用在量子色动力学中是夸克之间的胶子交换,弱作用在弱电统一理论中是Z,W+,W-这些中间玻色子交换,都是不用时间的。这种描述已经取得了巨大的成就,早已成为现代物理学的基本内容。这些中间交换的媒介粒子的确是虚粒子,不满足质壳关系,所以,是不可以用仪器测量到的。它们只是一种数学描述,称为费曼图。但独立的媒介粒子可以测量到。
No comments:
Post a Comment