在数学中，泰勒公式是一个用函数在某点的信息描述其附近取值的公式。如果函数足够光滑的话，在已知函数在某一点的各阶导数值的情况之下，泰勒公式可以用这些导数值做系数构建一个多项式来近似函数在这一点的邻域中的值。泰勒公式还给出了餘項即这个多项式和实际的函数值之间的偏差。泰勒公式得名于英国数学家布鲁克·泰勒。他在1712年的一封信里首次叙述了这个公式，尽管1671年詹姆斯·格雷高里已经发现了它的特例[1]。拉格朗日在1797年之前，最先提出了帶有餘項的現在形式的泰勒定理。
泰勒公式- 維基百科，自由的百科全書 - Wikipedia
zh.wikipedia.org/zh-hk/泰勒公式
所谓动力系统，就是一个集合上的单参数变换群，或者一个相流。有离散动力系统和连续动力系统之分。
连续动力系统定义在一个拓扑空间上，称为状态空间或相空间，通常是微微分流形，可以是无限维的，一个动力系统就是一个向量场，对应于
相空间自同构群的李代数，是一个无穷维李代数（有什么性质？）。一个李群的单参数子群和李代数有一一对应。相空间还可以有其它的数学结构，如复结构，
辛结构，黎曼流形，泊松结构，测度空间等等。
给定一个动力系统可以研究它的结构稳定性，所谓结构稳定性就是它的相图结构具有小扰动下的拓扑不变性，可以刻画为具有道路连通邻域。
所有结构稳定的系统构成一个开集（开子空间？，是否稠密？）。两系统称为同构的，如它们在同一个伴随轨道上，同构的系统他们的相图结构只差一个拓扑变换。
轨道是相图结构的基本单位，是最小的不变集。轨道的并集是不变集。系统在不变集上的限制称为子系统，一个变换若和系统相容则称为是系统的对称，一个系统和它的
无穷小对称是可换的。系统可在其一个对称群轨道空间上决定一个动力系统称为系统的商动力系统或约化系统。
除了对称性和结构稳定性，还可以研究系统的轨道的周期性，回归性，渐近行为，系统可积性和是否包含混沌和遍历性。
对于轨道可以有分为不动点，周期轨道，和概周期轨道等，再复杂一点就是混沌。
混沌对立面就是可积性。可积的轨道就是规则的轨道，相邻的轨道动力学行为相似的，可积的轨道就是周围的轨道都有相似的行为，比如都在一个环面或扭曲的柱面内运动。
| 量子力學的核心不是採用這個觀念建構起來的 反而是把一個物理系統的所有可能狀態(以前我們比較喜歡用系統所處的時間,擁有的總力學能,總動量代表) 當成一群可以用線性方式互相表達的向量 把觀測物理量的行為~看成是對系統的一種干擾~把它變成另一總狀態(變成誰得看這個物理量的性質和"機會") 惯性_百度百科動量- 維基百科，自由的百科全書 - Wikipedia
zh.wikipedia.org/zh-tw/动量
高中物理教材內容討論:什麼是量子化(問題)
www.phy.ntnu.edu.tw/demolab/phpBB/viewtopic.php?topic=25167
2012年4月1日 - 6 篇文章 - 4 位作者
對應古典的想法能量量子化也就對應動量量子化. ... 物理系統的所有可能狀態(以前我們比較喜歡用系統所處的時間,擁有的總力學能,總動量代表)討論區第一版:徑動(precission)(何彥廷)
www.phy.ntnu.edu.tw › ... › 1997/6月-2001/4月間問題討論區資料
近代物理 標題:什麼是量子化(問題) | ||||
 1:KB＊30 (高中職)張貼:2012-04-01 15:31:36: 能量 量子 粒子 | ||||
| 在問這個問題前 我已經尋找過許多資料但仍然沒有得到解答 我的問題是: 量子化是什麼? 什麼物理量具有量子化? 而量子化的條件又是什麼? 之前有看到論壇上有一個題目 問到下列選項中何者具有量子化的現象 以我現在所學的物理 我只知道量子化是為了解釋能量的不連續 而將能量想成一個個的能量粒子(能量包) 所以希望有人可以替我解答 | ||||
| 2:黃福坤(研究所)張貼:2012-04-02 07:22:06: [回應上一篇] 能量 動量 量子 原子 | ||||
| 物理的模型 都是人想出來 試圖解釋自然現象的 量子化也是人想出來的一種模型 十九世紀初 很多實驗結果 無法用傳統能量 連續的觀念去解釋 提出 能量可能並非連續 而是有特定數值 (如氫原子光譜對應的能量 ) 對應古典的想法 能量量子化 也就對應動量量子化... 一個學說或模型是否被接受 就看其是否 能解釋現有現象 能自圓其說 且能用來預測新的現象 再度被檢驗 例如 能量若是量子化 為何早期卻被視為連續 對應 遠看山上的草似乎是連續一片 可是近看時 卻是分開來 不連續的! | ||||
| 3:Hydrogen Dioxide(研究所)張貼:2012-06-17 19:09:37: [回應上一篇] 電子 | ||||
宋朝文人雅士曾說 : 蓮花濁清漣而不妖, 可遠觀而不可褻玩焉。 遠看物體有時候因為視覺上的積分效應而覺得物體是連續的，但是近看時卻發現有很多很多的孔洞在其中。當使用電子顯微鏡的時候又可以看到更精細的表面起伏的結構。哈哈。 | ||||
4:Richtiger Mann榮譽點數29點(大學理工科系)張貼:2012-06-20 18:26:09: [回應第1篇] 原子 能量 量子 近代物理 動量 向量 能階 ,本留言獲[]給賞金 共 2 點 | ||||
| 我是覺得高中教材所說的量子化比較接近"舊"量子論的說法 也就是認為某些物理量的容許出現的數值不是沒有限制 反而用一些整數去決定的 依據我所了解的近代物理知識 量子力學的核心不是採用這個觀念建構起來的 反而是把一個物理系統的所有可能狀態(以前我們比較喜歡用系統所處的時間,擁有的總力學能,總動量代表) 當成一群可以用線性方式互相表達的向量 把觀測物理量的行為~看成是對系統的一種干擾~把它變成另一總狀態(變成誰得看這個物理量的性質和"機會") 這裡當然沒有辦法完全告訴你~我們這些被全世界大部分科學家公認的假設 如何解釋舊量子論的量子化(EX 氫原子的能階在這總"論說"下如何解釋) 可是可以依稀給你一個開頭的方法(如果很數學化,那也沒辦法~因為對理論最有效率理解,單刀直入的理解常常是數學) 所謂的對物理系統的干擾~也就是將這個表達這個物理狀態的向量(以後簡稱態向量)變成另一個態向量~ v-------> v' 其實也就是一種函數,想一想多項式"函數"~不就是把所有的實數~透過多項式的運算對應到另一個實數嗎? 同樣的道理對物理系統所有可能的狀態也是類似的~不過對應的規則我們單單如下表示(今天取角動量做例子,或乾脆叫他角動量算符) L(v)=v' 很奇妙的是~自然界竟然希望物理算符也是線性的~ L(u+v)=L(u)+L(v) ,L(a*v)=a*L(v) 讓我們看看下面的方程式 L(v)=L'*v L'是一個數(可能實或虛的) 量子力學說~如果對一個L',v滿以上方程式 則物理系統處於v就會讓L的觀測值為L'(我們就這個方程式叫L的本徵方程式,v是屬於"本徵值" L'的本徵態向量) 也就是說~如果我們能將所有的態向量(u)以本徵態向量(vn屬於L'n)代表 u= c1*v1+c2*v2+....... L(u)的形勢就會很簡單~而且我們說~如果這些本徵向量組成的基底是互相垂直而且是單位向量 (cn)^2就表觀測u得出L'n之機率 大概來說~你用一些"古典"角動量的性質去找"量子"角動量算符的本徵值(這裡不拿能量算符(哈密頓算符)做例子~因為仔細思考~他將是最複雜的例子==)你會發現本徵值和整數是有關的~這粒沒辦法推給你看~可是必須提醒你~不是所有的算符都是量子化的(EX位置向量算符就不是~你可以自己用古典的性質思考看看)而且有沒有足夠的本徵象量組成"基底"的問題~對一個"物理量"可不可以觀測很重要~另外兩個物理量是否有共同的基底(技術上來說兩個可觀測量對不對易?)~直接關係到到兩個物理量可不可能同時觀測出固定值的問題(也就是含意較廣的不確定性原理,但至少我們有信心知道兩物理量觀測值標準差的不等式~) 我對近代量子論的解釋比較數學話一點~也可能有錯~希望有人幫我補充~讓量子力學的核心能比較淺顯易懂的傳遞出去^^ [ 這篇文章被編輯過: Richtiger Mann 在 2012-06-20 19:09:32 ] [ 這篇文章被編輯過: Richtiger Mann 在 2012-06-20 19:20:53 ] [ 這篇文章被編輯過: Richtiger Mann 在 2012-06-20 19:29:39 ] | ||||
| 5:Hydrogen Dioxide(研究所)張貼:2012-06-21 00:36:58: [回應上一篇] | ||||
這是一個很有意義且趣味的討論(對我來說啦!因為我物博一了,或許很多時下學生對物理超恐懼...), 很高興能看到你這番回應, 我剛有看了parts, 由於時間的關係只能留到明天或之後討論... 對了其實我要問為甚麼當年費曼會說了這麼一句話: 物理方程幾乎都是線性的,只要能了解線性方程, 基本上我們已經了解這個世界的一大半了? | ||||
| 6:Richtiger Mann榮譽點數29點(大學理工科系)張貼:2012-06-21 13:05:04: [回應上一篇] 動能 能量 相對論 轉動 | ||||
| 你問的問題其實牽涉的範圍很廣耶~ 我覺得這個問題可以從數學技巧,物理學家的世界觀或實驗上的方面來討論 因為我對數學方面比較熟悉~所以這方面我會多講一些 數學技巧上大家當然比較喜歡用簡單,但深刻表達物理意義的方法表達物理現象 就拿電磁學來說~我們所使用的梯度璇度散度不就是線性的嗎? 雖然一般化~非線性的形勢似乎比較誘人 但想想人類最基礎的運算~不就是加法乘法嗎 所一就算是很複雜的函數我們不是也很希望用冪級數(可以說是無窮多項的多項式,為高中生理解方便解釋一下)去逼近嗎 所以線性不但運算方便~而且可以很簡潔的推論出很多現象(向傅立葉的能量定理(也就是任意波的總能量是個別基態波能量的總和),系統總動能為質心和轉動動能之和) 在數學上深刻地告訴我們線性的假設是很符合(接近)大自然的 在物理學家的哲學上,大部分的科學家都接受時空是均勻的事實(也就造就了勞倫茲轉換較簡潔的形式)就算是廣義相對論,愛因斯坦也一在地相信,在某些條件下,小區域的地方俠義相對論是對的(也就是某一總程度上來說,以前教育灌輸給我們的歐基里德幾何在這宇宙是對的,不過這段敘述甚至是一個千真萬確的數學定理,微分幾何上的定理) (補充一下~狹義相對倫除了光速公設,物理量(尤其是時間長度)的操作性定義,其實邏輯上時空觀念和古典是相同的) 物理事實證的學科~雖然在邏輯上我們沒有理由相信哪一些觀念一定是對的 但是如果實用,我們就不如戒急用忍吧 不過線性也只不過是一種語言 他正代表著在人的靈魂裡某種堅定地信仰(有點像幾何學第五公設被質疑前人類的想法) 以上就是我的看法
结绳与量子计算 王正汉 !美国微软研究院! !"#"年$月" !!古人结绳记事%延续祖先的思维#我们用绳 圈来描述粒子的轨迹$记录它们的运动$进而探 讨绳圈数学的应用%%%拓扑量子计算% 绳圈的数学叫纽结论#是一门趣味盎然的学 科%在此我们仅介绍新的纽结不变量%%%琼斯多 项式! &'()* + ', - ('./0, "及其在量子计算中的应 用%如果读者有兴趣#我们推荐姜伯驹教授的 书&绳圈的数学%纽结论不仅是一门高深的数学 理论#也在物理#生物和量子计算机学科中有许多 的应用%从上世纪八十年代#量子力学的思想深 刻地影响着拓扑学的发展#形成量子拓扑学%留 美数学家林晓松教授! #123 % !""3 "对量子纽结论 的发展作出了很多开创性的贡献%谨以此文纪念 这位重要的拓扑学家%他所钟爱的量子纽结论正 走出数学#成为现代科技的一个有机部分% 上半部 无论是系领带#还是系鞋带#我们都是在用绳 子打结%但日常生活中的结和数学家们研究的结 有所不同%首先数学家用来打结的不是绳子#而 是理想化的绳子%%%曲线$其次数学家的结是一 个绳圈的模型%%%闭路线圈#也就是说绳子要首 尾相连%如果不是首尾相连#那么不管多么复杂 的结都能解开#也就是说变成直线段% 纽结论是研究理想化的结的一门数学学科# 它是拓扑学的一个重要分支%平面上的圆代表数 学家最简单的纽结#叫做平凡结%一个不能变成 圆的纽结叫做非平凡结%是否存在非平凡结呢' 只要我们用绳子做一些实验#就不难相信存在非 平凡结#也就是死结%下面的结是最简单的非平 凡结!左图"#叫三叶结%许多水手爱打这个结 !右图"& !三叶结" !!如果把右边的结头尾连在一起#但不可以从 任何地方剪断绳子#不管我们怎样做#我们都不能 把它变成平面上的圆%尽管很直观#但要证明存 在非平凡结却非易事#因为我们需要排除任何可 能的解法#但可能的解法多得无法想像%我们怎 样才能肯定所有的解法都试过了呢' 下面我们看 看拓扑学家怎样解决这个问题的% ! !纽结论 !"! !纽结 拓扑学家用曲线打结%曲线的严格数学理论 要用到微积分%为了避免这些知识#我们将用直 线段打结%因为光滑曲线可以看成由很短的直线 段构成的#所以这样得到的理论跟用曲线得到的 理论是等价的%但这个理论只用到非常初等的 知识% 现在我们严格定义我们的研究对象%如果有 一些直线段#它们可以长短不一#然后一段接一段 地把它们在空间连在一起形成一个闭线圈%如果 构成闭线圈的任何两条直线段或者不相交或者只 交于一个端点#我们就把这个闭线圈叫做一个几 何纽结%比如下面的几何纽结分别代表平凡结和 三叶结%平面上的任何一个多边形都是一个几何 纽结%显然存在无数多的几何纽结% !平凡结和三叶结" # !"#"年!第$1卷!第2期!! !!!!!!数学通报 拓扑学的一个基本特征是不关心物体的长 短#厚薄#粗细%对拓扑学家来说#所有大大小小 不同形状的三角形都代表同一个的纽结%%%平凡 结%不仅如此#所有平面上的多边形都代表同一 个纽结%如果我们是用绳子打结#这很容易理 解%由绳子做成的三角形是很容易变成四边形# 五边形%反过来也一样#四边形和五边形也可以变 成三角形%尽管我们的理论将会是基于由直线段 打成的结#但我们可以用绳子打成的结来思考% 为了交流方便#我们引进一些名词%一个几 何纽结上的任何一条直线段#我们都叫它是这个 几何纽结的一条边%拓扑学家只关心纽结的所谓 拓扑性质%像一条边有多长是不重要的%为了研 究几何纽结的拓扑性质#我们会引进一个拓扑等 价关系%两个拓扑等价的几何纽结将会被看成是 同一个拓扑纽结#简称纽结%从概念上来讲#纽结 和几何纽结是完全不同的%几何纽结是具体的# 纽结是抽象的% 严格的讲#一个纽结是由所有拓扑等价的几 何纽结所形成的等价类%所以#一个纽结代表一 个由那些拓扑等价的几何纽结形成的集合%和数 类比#一个几何纽结像一个箱子里的苹果#而一个 纽结是箱子里苹果的数目%我们指出一个可能引 起的混淆&拓扑学家经常不分纽结和纽结类#提 到纽结而实际是指纽结类%我们说的纽结严格地 讲对应于拓扑学家的纽结类#而几何纽结对应于 拓扑学家的纽结% 几何纽结间的拓扑等价关系定义很复杂#这 也是我们需要考虑直线段的原因% 给定一个几何纽结#叫它! #和它的两条相 联的边#叫它们" 和#$假设" 的末端连在# 的 首端$用一条新线段连接" 的首端和# 的末端# 我们叫这一条新的线段%$ !见下图"如果%和! 别的边都不相交!但可以和" # # 重和"#我们可 以从! 的边中拿掉边" 和边# #然后加入%得 到一个新的几何纽结#叫它!&$我们把从边" # #到边% 或者反过来从边% 到边" # #的变换叫 做一个三角形变换$注意三角形变换的一种特殊 情况#在一条边的内部加一个点变成两条边#或 者反过来$如果由" # # # %所形成的三角形的内 部和! 的除" # #以外的任何边都不相交#我们 称这样的三角形变换为! '变换$两个几何纽结 ! 和!&是拓扑等价的如果! 能通过有限次的 ! '变换变成!&$我们以后将拓扑等价简称为 等价$ ! ! '变换" 如果! 是由!&通过一个三角形变换得到 的#那么! 和!&有时是等价的#有时是不等价$ 本节开始的平凡结可以从它右边的三叶结通过一 个三角形变换得到#但它们是不等价的$ 最简单的纽结是平凡结#它是包括所有三角 形在内的几何纽结的等价类$实际上#平面上所 有多边形都代表平凡结$给一个纽结#我们叫它 的任何一个几何纽结为它的一个代表$ 思考题# #%证明平面上所有多边形都可以通过有限次! 4 变换变成一个三角形% !%证明所有四边形#不限于平面上#都等价于三 角形% !%# !纽结不变量 我们都相信存在非平凡结#但怎样证明呢' 也就是说#存在一个几何纽结#无论一个人多么聪 明#花多长时间#做多少! 4变换#都不可能把这个 几何纽结变成一个三角形' 拓扑学家的想法很简 单#引进所谓的不变量%我们给每一个几何纽结 一个我们熟悉的量#像一个数#或者一个多项 式%这个量叫做不变量#如果这个量在任何! 4变 换下不变%即两个等价的几何纽结所得到的量是 一样的%但不等价的纽结也有可能得到同样的量% 定义不变量是一件很容易的事%譬如#我们 可以给所有平凡几何结# #给所有别的几何纽结 "%但这个不变量对于研究纽结来说#毫无用处% 考虑所有纽结形成的集合#从这个集合到实数的 任何一个映射都是一个纽结不变量%用这个想法# 我们可以定义一个有用#但很难计算的纽结不变 量&离散长度%给定一个纽结#把这个集合里的所 有几何纽结的边数的最小值取出来#这是一个正 整数%我们把这个正整数叫做这个纽结的离散长 度%它反映出如果真的用绳子打这个结#我们至 少需要一定长度的绳子%不难证明#平凡结的离 散长度是5 #而三叶结的离散长度是6%本节开始 的五边三叶结实际上需要六条边% 纽结论的重要问题是如何分类纽结%即给出 一个几何纽结的集合使得在这个集合里每一个纽 结都有而且只有一个几何纽结代表%拓扑学家希 望能找到一个完备的纽结不变量#即一个不变量 使得不同的纽结会有不同的不变量%如果我们有 这样一个不变量#纽结的分类就简化成这个不变 量的计算%存在不少的完备纽结不变量#但我们 还没有发现完备而容易计算的不变量#或许这样 的不变量是不存在的% 思考题# #%当离散长度足够大时#我们可以得到不同的纽 结%最小的离散长度使我们可以得到不同的 纽结是多少' 我不知道答案% !%在纽结上取个方向#我们就可以定义两条相邻 边的角度%用这些角度定义一个纽结不变量% !%$ !纽结投影 想研究纽结#我们就要有办法把所有纽结都 画出来%拓扑学家的办法是利用纽结在平面上的 投影%前面我们已经看到#在平面上是画不出非 平凡结的%纽结是我们所生存的空间的一个现 象%如果你听说过四维或更高维空间#在那里面 同样画不出非平凡结%为了能在平面上表示出非 平凡结#我们就必须记住纽结的一些空间性质% 给一个几何纽结#想像在它的后面远处有一 个屏幕%如果我们把这个几何纽结投影到这个屏 幕上会是什么样子' 一条线段的投影是一条线段 或是一个点#所以纽结的投影是一个由线段组成 的闭路#但可能有很多交点&双重点#三重点等等% 如果我们稍微移动一下后面的屏幕#我们可以做 到这样&没有任何一条直线段被投影成一个点#而 且只有直交的双重交点$任何其它类型的交点都 叫奇点%没有奇点的纽结投影叫正则投影%这又 是这样一个事实#虽然不难相信#但严格证明并 不显然%有兴趣的同学可以自己试试% " ! !奇点" 一个正则投影的每一个双重点都是两条边投 影的交点%这两条边一上一下!每一个双重点都 是两个点的投影#我们把离屏幕近的那一点所在 的那条边叫下% "如果我们在一个几何纽结的一个 正则投影的每一个双重点处都记下那两条边的上 下关系#我们就得到了一个纽结图%我们把带有 上下信息的双重点称做交叉点%交叉点分为上交 叉点和下交叉点& !交叉点" 如果可以用曲线#通常我们会把下面那条边 画在平面上#而上面的那条边在双重点附近画在 平面上面%但如果只能用直线段#我们可以把上 面那条直线段变成两条线段稍微高于平面#使得 原来的端点的投影都在平面上%我们把这样由正 则投影图得到的图叫纽结图%一个几何纽结和它 的任何一个纽结图是拓扑等价的#所以在很多情 况下#我们只需要考虑纽结图% !正则投影" 一个纽结会有很多纽结图#但它们全都等价% 给定两个纽结图#怎样决定它们是否代表同一个 纽结呢' 原则上我们已经知道答案&只要考虑所 有! 4变换的正则投影%实际上这个办法却很难应 用#因为! 4变换中的三角形可以很大%纽结论里 的一个著名定理把! 4变换简化到下面三组变换# 叫瑞德迈斯特! 7)/8).)/*9): "移动7; # 7;; # 7;;; #反之亦然% !瑞德迈斯特移动" 我们可以证明& 瑞德迈斯特定理!两个纽结图( 和(&所代 表的纽结是等价的当且仅当( 能通过有限次的 瑞德迈斯特移动变成(&$ 由于这个定理#纽结论也可以只研究纽结图 和它们在瑞德迈斯特移动下的等价类%以下一组 图证明7;;;移动可以用! 4变换实现% ! %&&&与! '变换" 思考题# #%证明只有一个或两个交叉点的纽结图总表示 平凡结% !%证明所有纽结的集合是可数的#即我们可以把 它们和正整数一一对应% # !琼斯多项式 #1<$年#新西兰数学家琼斯! =%&'()* "发现 了一个全新的纽结不变量#叫做琼斯多项式%琼 斯多项式的发现引起了纽结论里的一场革命#进 而推动了一个新的拓扑方向%%%量子拓扑的产 生%琼斯多项式其实不是严格意义下的多项式# 因为它的变量的次方可以是负整数和分数% 我们首先引进一些定义和记号$假设( 是一 个有)个交叉点的纽结图$如果给每个交叉点一 个标号" 或# #我们就叫( 的一个态#记作*$给 定( 上一个交叉点和一个标号" 或# #我们可 以在这个交叉点的附近做一个手术! *>: ? ): - "& !手术" 上图里的手术的规则是这样的&在交叉点的 附近#从上面的边逆时针旋转到下面的边#上面 的边会扫过两个区域!一个交叉点把平面分成四 个区域"叫" 区#另外两个叫# 区$" 手术就是 打通" 区#而#手术就是打通# 区$ 假设+是一个参数变量$给定( 的一个态* # 那么每一个交叉点都有一个" 或#$如果是" #我 们就做" 手术#如果是# #我们就做#手术$每一 个手术都从纽结图中去掉一个交叉点#当所有手 术完后#我们得到平面上的一些闭线路#这些闭 线路的个数记作, ! * " $我们用* ! " "记态*上" 型交叉点的个数#同样用* ! # "记态*上# 型交叉 点的个数$ 让# * $ @+ * ! # " A* ! " " $ (! A+ # ! A+ A # ! " , ! * " $ 定义# ( $ @ % # * $ #这个和一共有! ) 项$我们叫# ( $为( 的考夫曼! B%C0>DD.0( " 括号% 每个纽结图有两个方向&从图上的某点出发# 沿纽结图朝前或后走一圈%取定纽结图( 的一个 定向#每条边都有一个方向%我们给每个交叉点 一个符号&正负#如下& !符号" 改任何一个箭头#符号正负#互换$注意到 如果我们取得是另一个方向#因为每个交叉点的 两条边方向同时改变#所以这个符号是不依赖于 纽结的方向的$ 把( 的所有交叉点的符号的和记作- ! ( " $ 最后定义纽结图( 的琼斯多项式 . ! ( $ + " @ ! A# " - ! ( " ( + 5- ! ( " $ ( # ( $ $ 可以证明. ! ( $ + "在瑞德迈斯特移动下不 变#所以确实是一个纽结不变量$这就是著名的 琼斯多项式$给一个纽结! #它的琼斯多项式 . ! ! $ + "定义为! 的任何纽结图的琼斯多项式$ 平凡结的琼斯不变量是A+ # ! A+ A # ! #因为圆只 有一个态&无交叉点#但有一个闭线路$而三叶结 的琼斯多项式是. ! + " @ ! +E+ 5 A+ $ "! A+ # ! A + A # ! " $所以三叶结一定是非平凡的$ 由多个不相交的纽结组成的多条曲线叫链 环$拓扑学家除研究纽结外#也对链环感兴趣$ 琼斯多项式可以定义在链环上#但链环必须有定 向$如果处理好定向#我们前面的所有讨论都对 链环适用$我们把细节留给读者$给一个定向链 环/ #它的琼斯多项式也记作. ! / $ + " $ 有了链环的琼斯多项式#我们可以有一个计 算琼斯多项式的线团! *F)/( "关系式$假设/ E 是一个链环图!带定向"#而0是/ E 上的一个交 叉点$如果我们把交叉点0的两条边上下换了# 我们就有一个新的链环图#记作/ A $我们也可 以顺方向光滑/ E #得到另一个链环图/ " !见下 图" $我们可以证明#这三个链环的琼斯多项式 满足以下恒等式& + A# ( . ! / E $ + " A+ ( . ! / A $ + " @ ! + # ! A+ A # ! "( . ! / " $ + " !线团关系式" 用线团关系式#我们可以递推得计算琼斯多 项式$因为每一个定向链环的琼斯多项式. ! / $ + "除以A+ # ! A+ A # ! 还是一个链环不变量#我们定 义1 ! / $ + " @ . ! / $ + " A+ # ! A+ A # ! $这样平凡结的不变量 就变成#$1 ! / $ + "也叫琼斯多项式#也满足线团 关系式$ 琼斯多项式是一个非常重要的链环不变量$ 然而从定义或线团关系式进行计算#非常复杂$ 如果一个链环有个)交叉点#那么计算它的琼斯 多项式就需要做! ) 个和$学过幂指数的都知道 指数增长的速度&据估计整个可见宇宙里的基本 粒子数不会超过! !"" $所以计算!""个交叉点的 链环的琼斯多项式#要加的和数已经不可思议$ 但有没有别的聪明办法高效地计算链环的琼斯多 项式呢' 数学家们相信高效的算法是不存在的$ 但是如果我们有量子计算机#我们就可以高效的 逼近琼斯多项式的值$下半部我们看看量子计算 机是怎样做到的$ 思考题# #%把每一个交叉点的上下互换#琼斯多项式怎样 变化' !%改变链环的方向#琼斯多项式怎样变化' 5%是否存在非平凡结而它的琼斯多项式和平凡 结是一样的' 这个问题极难#我们还不知道 答案% 下半部 大卫(希尔伯特! #<6! % #1$5 "是伟大的德国 数学家%#1""年他在巴黎国际数学家大会上提出 了!5个当时未解决的数学问题%这!5个问题对 上个世纪前半叶的数学发展产生了深远的影响 其中的第十个问题是&给定一个多元整系数多项 式2 ! 3 # 4 #)# - "#给出一个算法来决定2 ! 3 # 4 # )# - "是否有整数解%希尔伯特并没有定义什么 是算法#而且他下意识的相信算法是存在的% #13"年数学家证明不存在算法可以解决这个问 题%但早在#156年#英国数学家阿兰(图灵! G% H>:/( ? # #1#! % #12$ "就发表了题为*可计算数及 在决断问题中的应用+的文章%在这篇文章中图 灵严格定义了算法#并证明存在数学问题是没有 算法来求解的%图灵定义的算法被称作图灵机% 是计算机理论奠基性的工作之一%图灵对逻辑 学#密码学和现代计算机理论都有巨大的贡献% 在二次世界大战中#他帮助盟军解密了德国的著 名I(/ ? .0密码机器#加快了盟军的胜利% 学过数学的人都有算法的经验%即使一个问 题有算法可解#也不意味着这个算法是可行的% 理论计算机的一个重要方向就是研究高效! )DD/4 J/)(9 "的算法%比如著名的求两个正整数最大公 因子的欧几里德算法%欧几里德算法不但简单# 而且高效%然而另一个问题&给定一个正整数# 找出它的素因子分解%不但至今没人能找到高效 的算法#数学家相信高效的算法根本就不存在% 所以很多秘密都是基于这个假设%如果某一天有 人发现了一个高效的素因子分解办法#很多国家# 银行和个人的秘密#包括因特网上的很多交易# 就会被泄漏%令人惊奇的是# #11$年美国数学家 肖尔! K%LM': "发现量子计算模型可以高效地进 行素因子分解%量子计算模型是基于量子力学理 论的计算模型%它的实现非常困难%实现量子计 算的一种办法是基于纽结论%%%拓扑量子计算% 怎样用纽结计算呢' $ !计算模型 每一种物理理论#都伴随着一种计算模型% 经典物理的计算模型就是我们现在的计算机%每 一种计算模型都可以高效的解决一类问题%因为 量子物理包含经典物理#所以任何高效的经典算 法都可以看成高效的量子算法%我们希望量子计 算可以解决一些经典计算不能高效解决的问题# 像素因子分解%虽然我们有高效的量子素因子分 解算法#且没有高效的经典素因子分解算法#但 我们并不能证明高效的经典素因子分解算法是不 存在的%所以我们也就不知道量子计算是否真的 比经典计算更高效% $"! !公开的秘密 研究算法效率的理论叫计算复杂性$计算复 杂性考虑我们是否能够高效地利用我们的资源来 解决一类问题$资源可以是很多东西#比如时 间#记忆#也可以是精确度#但我们不考虑财富$ 我们用一个例子来说明它的用处$假设两个离得 很远的网友在网上下一盘重要的围棋#很久他们 还没有下完#所以决定停下来以后再下#但谁都 不想下最后一招棋#给对手时间仔细研究对策$ 假设他们不想任何别人参与#怎么办呢' 利用计 算复杂性#我们可以有这样一个可行的办法&把 围棋盘想像成平面坐标系#那么它的每个位置都 可以记成一对数! |
![\begin{displaymath}u=\sqrt[3]{-\frac{q}{2}+\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}} \quad v=\sqrt[3]{-\frac{q}{2}-\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}\end{displaymath}](http://episte.math.ntu.edu.tw/articles/sm/sm_17_07_2/img3.gif)
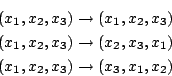
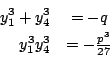
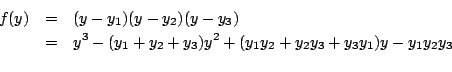
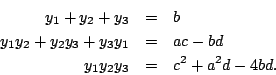
No comments:
Post a Comment