而可写出循环边界条件下晶体中各原子作微小振动的牛顿方程,并得到3nN个简谐近似解, 二次量子化
www.docin.com › 论文 › 论文指导/设计
轉為繁體網頁
2014年5月9日 - 计算结果给出了收敛的简谐子谱分布,并发现了许多简谐子软模.用这些软模 ..... 在简谐近似下,西的展开式只取到二次项,从而巾=去∑∑中砒。,(,, '{k ... …e, 从而可写出循环边界条件下晶体中各原子作微小振动的牛顿方程,并得到3nN个简谐近似解.这种解经二次 ..... http://www.docin.com/p-808704494.html.
www.docin.com › 论文 › 毕业论文
轉為繁體網頁
2011年2月6日 - 2:根据简并情况下光纤参量放大的理论模型,在小信号近似下数值解非线性耦合波方程。 ..... 了详细描述;推导了简并情况下的非线性耦合波方程组并得到近似解,并在小信号情况下 ... 电极化率为零,二阶非线性效应产生的二次谐波及和频,只存在于无反对称性的晶体中。 ..... http://www.docin.com/p-799394603.html.
www.docin.com › 论文 › 毕业论文
轉為繁體網頁
2011年5月3日 - 学位论文作者签名:墒P糙浩I 1 日期:劲口15、/・ 学位论文版权使用授权书本学位论文作者和指导教师完全了解东北大学 ..... 其特点是直接求解问题的基本方程和相应定解条件的近似解。 ..... http://www.docin.com/p-898450547.html.
www.docin.com › 生活休闲 › 科普知识
轉為繁體網頁
2009年12月26日 - 2几个近似公式的比较要比较上述近似公式,首先要求出(4)的精确解。 3讨论为求 ... 空气阻力随着摆角的增加而增加,这将导致单摆运动不能成为简谐运动,其周期也就失去了研究的意义。而且,摆角 ... 刘风祥单摆运动周期的近似解[期刊论文]-大学物理1999(11) 4.张继县. .... http://www.docin.com/p-834288816.html.
www.docin.com/p-179943603.html
轉為繁體網頁
2011年4月14日 - 简谐近似和简正坐标: 从经典力学的观点看,晶格振动是一个典型的小振动问题,由于质点间的相互作用,多自由度 ... iii 势能在平衡位置展开: 只保留的二次项称作简谐近似。 ... 3 2 2 2 1 1 2 N i i i i H p Q ω = = + ∑ 引入简正坐标的目的是为了使系统的势能函数和动能函数 .... http://www.docin.com/p-755231088.html.
www.docin.com › 论文 › 毕业论文
轉為繁體網頁
2011年4月1日 - 并由速度分布式得出了板周围空间声压分布的近似解。 ... 求解得到在简谐激振力作用下该板的强迫稳态振动解,并通过复化SIMPSON公式求解出不同激振频率下的空间声压分布情况。 ... 用表面振动的二次积分来表示声压,既可以用远场径向声强的二次球积分来表示声 ...... http://www.docin.com/p-681255685.html.
Electromagnetic Waves in a Cubical Cavity
www.slideserve.com/sonya-mcpherson/5972115 - 轉為繁體網頁
2014年10月30日 - 卢瑟福模型. 原子核式结构模型—. 第一章小结. 原子序数为Z 的原子的中心,有一个带正电荷的核(原子核),�...
Electromagnetic standing waves in a cavity at equilibrium with its surroundings cannot take just any path. They must satisfy the wave equation in three dimensions:
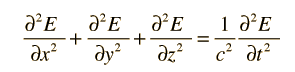 The solution to the wave equation must give zero amplitude at the walls, since a non-zero value would dissipate energy and violate our supposition of equilibrium. To form a standing wave, the reflection path around the cavity must produce a closed path. The boundary conditions can be met with a solution of the form:
The solution to the wave equation must give zero amplitude at the walls, since a non-zero value would dissipate energy and violate our supposition of equilibrium. To form a standing wave, the reflection path around the cavity must produce a closed path. The boundary conditions can be met with a solution of the form:

Substituting this solution into the wave equation above gives

which simplifies to

| Index
Rayleigh- Jeans references
Blackbody radiation concepts |
| Go Back |
http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/rayj.html#c3
How many modes in the cavity?
From the standing wave solution to the wave equation we get the condition
 . .
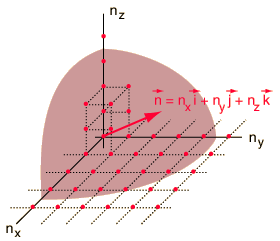 The Rayleigh scheme for counting modes. The Rayleigh scheme for counting modes.
After Richtmyer, et al. | We need to evaluate the number of modes which can meet this condition, which amounts to counting all the possible combinations of the integer n values. An approximation can be made by treating the number of combinations as the volume of a three-dimensional grid of the values of n, an "n-space". Using the relationship for the volume of a sphere, with the n values specifying the coordinates along three "n" axes, gives |
 . .
|
This has a couple of problems, however. In using a sphere, we have used both positive and negative values of n, whereas the wave equation solution uses only positive definite values. Therefore we must take 1/8 th of the volume above. Another technical problem is that you can have waves polarized in two perpendicular planes, so we must multiply by two to account for that. Then the volume can be taken to be a measure of the number of modes, becoming a very good approximation when the size of the cavity is much greater than the wavelength as in the case of electromagnetic waves in finite cavity. Using the relation obtained for the values of n, this becomes
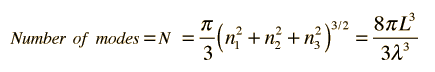
| Index
Rayleigh- Jeans references
Richtmyer, et al.
Ch. 5
Blackbody radiation concepts |
| Go Back |
How many modes per unit wavelength?
Having developed an expression for the number of standing wave modes in a cavity, we would like to know the distribution with wavelength. This may be obtained by taking the derivative of the number of modes with respect to wavelength.
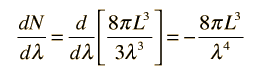
The negative sign here reveals that the number of modes decreases with increasing wavelength. Now to get the number of modes per unit volume per unit wavelength, we can simply divide by the volume of the cubical cavity.
 Note that this does not involve approximating a sphere with a cube! The sphere we used in calculating the number of modes was a sphere in "n-space", allowing us to count the number of possible modes. Also, the use of a cubical cavity for the calculation just allows us to reduce the geometrical complexity of the development, but the final result obtained is independent of cavity geometry.
Note that this does not involve approximating a sphere with a cube! The sphere we used in calculating the number of modes was a sphere in "n-space", allowing us to count the number of possible modes. Also, the use of a cubical cavity for the calculation just allows us to reduce the geometrical complexity of the development, but the final result obtained is independent of cavity geometry.
| Index
Rayleigh- Jeans references
Blackbody radiation concepts |
| Go Back |
How much energy per unit volume?
Assigning energy to the electromagnetic standing waves in a cavity draws on the principle of equipartition of energy. Each standing wave mode will have average energy kT where k is Boltzmann's constant and T the temperature in Kelvins. Letting u represent the energy density:

This is an important relationship in classical electromagnetic cavity theory. It can also be expressed in terms of the frequency ν by making use of the chain rule and the wave relationship:
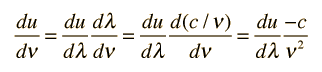
The minus sign here just reminds us that a decrease with wavelength implies an increase with increasing frequency. The magnitude of the energy density dependence on frequency is given by:
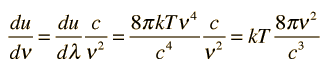
Note that this is the classical result which was used in the Rayleigh-Jeans Law, but led to the ultraviolet catastrophe. It produces good agreement in the low frequency limit, but for higher frequencies the Planck radiation formula must be used.
| Index
Rayleigh- Jeans references
Blackbody radiation concepts |
| Go Back |
Radiated Energy as a Function of Wavelength
If we consider energy radiated perpendicular to a small increment of area, then it must be noted that half of the energy density in the waves is going toward the walls and half is coming out if the system is in thermal equilibrium. Evaluating the power seen at a given observation point requires a consideration of the geometry:
For perpendicular radiated energy
 but at an angle θ, the effective area will be Acosθ and the effective speed will be c cosθ, so the radiated energy will be reduced to
but at an angle θ, the effective area will be Acosθ and the effective speed will be c cosθ, so the radiated energy will be reduced to
 For a given observation point near a radiating surface, the power will be the average power from all directions, and the average gives another factor of 1/2.
For a given observation point near a radiating surface, the power will be the average power from all directions, and the average gives another factor of 1/2.
Having averaged over all angles, the calculated radiated power per unit wavelength is finally
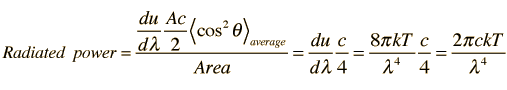
This is the Rayleigh-Jeans formula. The fact that it failed to predict the spectral distribution from hot objects was one of the major unresolved issues in physics at the beginning of the 20th century.
To express this in terms of frequency, an application of the chain rule as was done above with the energy density yields a radiated power per unit frequency:
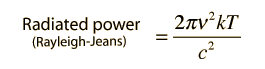
| Index
Rayleigh- Jeans references
Blackbody radiation concepts |
| Go Back |

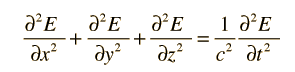



 .
.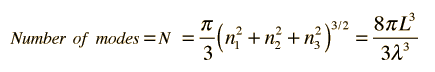
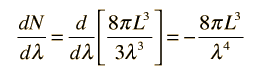


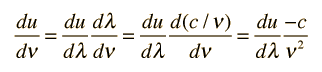
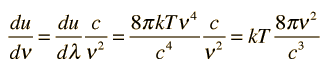


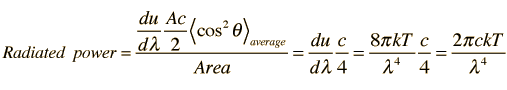
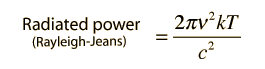

 The Rayleigh scheme for counting modes.
The Rayleigh scheme for counting modes. .
.
No comments:
Post a Comment