The “Higgs field” (‘scalar field’) is a postulate that is nothing more than a theoretical variation upon the Aether concept. As many know conceptions of the Aether likewise posits a ‘universal field’ or ‘universal essence’ by way of which particles acquire their substance and sustenance. So, how does one explain the origin of “mass”? One simply invents a ‘universal field’ consisting of quantum “particles” (or “ripples”) of much greater “mass” which smaller particles can supposedly ‘couple to’ as they interact with said “field”. The electromagnetic field has its quantum particle i.e. the “photon” so why not invent a likewise “field” for “mass”.
How is trying to explain the acquisition of “mass” as being the result of interactions with a hypothetical “field” of particles having greater “mass” supposed to be an explanation for how particles acquire their “mass”? That doesn’t seem explain the supposed ‘origin’ and/or acquisition of “mass”’. Yet, the Aether (“charge”) functions along similar lines in some respects but it is not by way of a ‘coupling’ dynamic.
L. Krauss goes on to assert that Life and Existence is all just a happy accident - “We’re only here because we have mass; and it’s because of the Higgs field”. This is like listening to an astrophysicist who asserts that ‘We’re only here because we are stardust’. Or, ‘We’re only here because there are neutrinos’ – or something. Then:
I’m amazed if it’s there because it’s really a theoretical edifice that’s been built over fifty years that requires something fantastical: this field throughout space and it seems almost too good to be true.
Those who espouse the existence of Aether have proposed this fundamental for centuries and little known, or understood as such, a variety of the most ancient mythologies across the globe utilize metaphor and allegory in relation to the activities of said Fundamental Substance predating even the origin of the conceptual term ‘Aether’ via Aristotle. Where hast thou been? And then:
When you’re a theoretical physicist like the two of us its weird when you’re sitting around at night and you invent something; to think that maybe Nature accepts that, or follows that rule.
… “Invent” something? The effort only reinvents the age’s old concept of the Aether whether termed as such; or not, similar in fashion to Einstein’s reinvention of same as a “space time fabric”. Ten or twenty billion dollars is being spent to postulate by way of inference the same basic fundamental principle?? Seriously? And then; the shameless plug from B. Green (I actually like B.Green):
Certainly from the perspective of convincing funding agencies to continue this line of research it’s better to have something that you can point to than something that is a null result; we’re excited about that.
Well of course, as long as funding is continued so that physicist can have a feel good moment about even the inference of a ‘universal field’ even though the same idea had been put forth long ago. Next up, Supersymmetry, which doubles the number of “particles” in the particle zoo again with “superpartners”, waiting in the wings to justify the continued funding and the further pursuit of more “mass”-ively expensive and fantastically short-lived ‘inference findings’. Can anyone spare a few moments to solve the supposed “energy crisis” with any of these inferred 'findings'?
So, consider this brief comparison:
A charged particle inevitably produces an electric potential around it, and it also feels the potential created by itself. This leads to an infinite "self-energy" of the electron.
(...)
Once there exists anti-matter, which can annihilate matter or be created with matter, what we consider to be an empty vacuum undergoes a fluctuation to produce a pair of electron and positron together with photon, annihilating back to vacuum within the time interval allowed by the uncertainty principle (a). In addition to the effect of the electric potential on itself (b), the electron can annihilate with a positron in the fluctuation, leaving the electon originally in the fluctuation to materialize as a real electron (c). It turns out, these two contributions to the energy of the electron almost nearly cancel with each other. The small size of the electron was made consistent with electromagnetism thanks to quantum mechanics and the existence of anti-matter. – Introduction to Supersymmetry
Key concepts underlined: Yet, for someone to put forth the Aether and posit that the One Primary Substance undergoes Motion (‘fluctuations” above) to such extent that from ‘self-induced’-‘self-differentiations’ (“self-energy” above) due to these Motions, “matter” (“real electrons” above as an example) may be ‘precipitated’ or ‘materialize’ (just as described above) - destined to return to That Source (“annihilating back to the vacuum” above) that the cycle continues - becomes somehow unusual?? How so when this is principally and conceptually what has been put forth in other terms?
Consider it again:
The primary substance, thrown into infinitesimal whirls of prodigious velocity, becomes gross matter; the force subsiding, the motion ceases and matter disappears, reverting to the primary substance." - Nikola Tesla
By the power of Philosophy, Experiment, and Reason the existence of a Fundamental Essence was derived long before latter-day “modern physics”. The principle of a fundamental “universal field”, as a principle, is not new and far greater work has been done with much less and NO public dollars (Nikola Tesla, Aetherometry & Eric Dollard etc). Goodness me Tesla had nothing but brass, copper, and wood but far greater noble aims having come to the same conclusion.
I don't mean to sound cynical but am I missing something (?) - because I’m seriously not impressed with any of this. Someone help me out here.
If there be nothing new, but that which is
Hath been before, how are our brains beguiled,
Which, labouring for invention, bear amiss
The second burden of a former child. - Shakespeare
Of Particular Significance
Conversations About Science with Theoretical Physicist Matt Strassler
2. Why the Higgs Field is Non-Zero on Average
© Matt Strassler [October 14, 2012]
This is article 2 in the sequence entitled How the Higgs Field Works: with Math. Here is the previous article.
How does it happen that the Higgs field has a non-zero average value in nature, while the other (apparently-)elementary fields of nature that we know about so far do not? [Very fine point: other fields excepting the lowest-level gravitational field, called the “metric”, that helps establish the very existence of space and time.]
First, it is impossible for fermion fields to have a large constant non-zero average value in nature. This is related to the difference between fermions and bosons; bosons can be non-zero on average, but fermions really can’t. So we can forget about electrons (and their cousins the muons and the taus), about neutrinos, and about the quarks. [Fine point: Fermions can pair with each other or with anti-fermions to make composite bosons, and those composite bosons can be non-zero on average. In fact this is true of the up and down quarks and their antiquarks, and it is true of electrons in a superconductor. But that’s a long story, and not our immediate concern.]
What about the photon field, the gluon field, the W and the Z field? These are all bosons. In principle these fields could have a constant non-zero value on average throughout the universe. It is experiment, not theory, that says this isn’t the case. A large non-zero value for the electric field would have all sorts of effects that we do not observe, including most significantly an apparent violation of rotational invariance at large distance scales. The electric field is a vector (spin-1) — it points in a particular direction — so if it were non-zero, the direction in which its non-zero value points would be different from the other directions. See Figure 1, lower left.
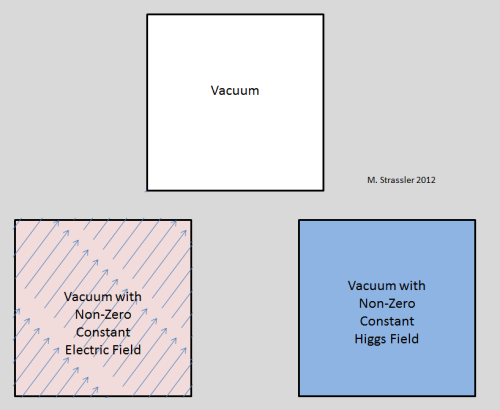 By contrast the Higgs field is a scalar (spin-0) — it does not point anywhere. Other (non-elementary and non-relativistic) scalar fields include the density field of the air, the pressure field inside the earth, the temperature inside the ocean; at every point in space and in time, the density or pressure or temperature is just a number, whereas the electric field is a number and a pointing direction. So if the Higgs field has a non-zero value, it does not result in a preferred direction; see Figure 1, lower right. More bizarre is the fact that (because it is a relativistic field) it produces no preferred frame at all. For the density of the air, there is a preferred frame, because one is either at rest with respect to the air or moving through it. But this isn’t true for the Higgs field; all observers are at rest with respect to the Higgs field. Therefore the success of Einstein’s special relativity in describing all sorts of phenomena is not inconsistent with the presence of a non-zero value for a relativistic scalar field, such as the Higgs. In short the non-zero value of the Higgs field leaves the vacuum behaving much the way it does even when H=0; remarkably, you can only tells it’s there through its effects on the masses of particles (or by doing something dramatic, such as using the Large Hadron Collider to make Higgs particles.)
By contrast the Higgs field is a scalar (spin-0) — it does not point anywhere. Other (non-elementary and non-relativistic) scalar fields include the density field of the air, the pressure field inside the earth, the temperature inside the ocean; at every point in space and in time, the density or pressure or temperature is just a number, whereas the electric field is a number and a pointing direction. So if the Higgs field has a non-zero value, it does not result in a preferred direction; see Figure 1, lower right. More bizarre is the fact that (because it is a relativistic field) it produces no preferred frame at all. For the density of the air, there is a preferred frame, because one is either at rest with respect to the air or moving through it. But this isn’t true for the Higgs field; all observers are at rest with respect to the Higgs field. Therefore the success of Einstein’s special relativity in describing all sorts of phenomena is not inconsistent with the presence of a non-zero value for a relativistic scalar field, such as the Higgs. In short the non-zero value of the Higgs field leaves the vacuum behaving much the way it does even when H=0; remarkably, you can only tells it’s there through its effects on the masses of particles (or by doing something dramatic, such as using the Large Hadron Collider to make Higgs particles.)
The simplest way for the Higgs field to end up with a non-zero value throughout the universe would be if has a non-zero equilibrium value H0 that appears in its Class 1 equation of motion:
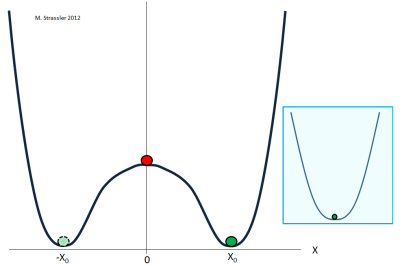
It isn’t instantly obvious, but the solution at H = 0 is unstable. The situation is analogous to the equation of motion for a ball in a bowl shaped like the one shown in Figure 2 — like the bottom of a wine bottle. This also has three equilibria, one at 0 and ones at ±x0. But clearly the equilibrium at 0 is unstable, in that even a tiny push will cause the red ball to roll far from x=0, a dramatic change. By contrast the equilibrium at x=x0 is stable, in that any little push will just cause the green ball to oscillate with small amplitude around the point x=x0, a not very dramatic change. (The same is true for the light green ball at x=-x0.) In a similar way, although H = 0 is a solution to the Higgs field’s equation, our universe’s history has been complex enough to assure that the Higgs field has been knocked around a bit, and so it can’t possibly be sitting there. Instead, the Higgs field ends up in a solution with a non-zero value, a situation which is stable.
 We have known for decades, from a combination of experiment and theory, that the Higgs field’s value (which we traditionally call “v”) is 246 GeV. That tells us something about those two constants a and b: in particular
We have known for decades, from a combination of experiment and theory, that the Higgs field’s value (which we traditionally call “v”) is 246 GeV. That tells us something about those two constants a and b: in particular
Now, although I’ve set things up so that H could be either v or -v, it doesn’t matter whether the value of the Higgs field is positive or negative (actually there are even more possibilities, see below); the world comes out looking the same, with the same physics, because nothing depends on the overall sign of H. This isn’t instantly obvious, but it’s true; one hint is that wherever you find H in the equations described in my overview of how the Higgs field works, it’s always H2 that appears, not H alone — and H2 doesn’t depend on whether H = v or H = -v. [Fine point: In fact, H is a complex field, with a real and an imaginary part, so H can be v times any complex number z with |z|=1; and in fact it’s always H*H = |H|2 that appears in the equations, which is independent of z. Even that’s not the whole story! but it’s good enough for today.]
If you find a way (perhaps using the proton-proton collisions at the Large Hadron Collider) to push or disturb the Higgs field a little bit somehow, it will wiggle back and forth — i.e., waves will develop, of the form
Wikinews has related news: Prospective Nobel Prize for Higgs boson work .... The condensate value is described by a quantum field with an expectation value, ...
In quantum field theory the vacuum expectation value (also called condensate ... The Higgs field has a vacuum expectation value of 246 GeV This nonzero value ...
Vacuum Expectation Value. The Higgs potential has the shape of a “mexican hat”. It has a minimum which is not at <φ>= 0. Known as the vacuum expectation ...
the most general, non-trivial, renormalizable potential is: V = ½µ2Φ2 + ... The Higgs mass and the vacuum expectation value of the Higgs field can be written in ...
Oct 14, 2012 - (Bottom Right) A non-zero value for the Higgs field does not change the ... where a and b are constants (whose squares are positive! notice the plus ..... of why the Higgs vev (vacuum expectation value) has the particular value ...
Mar 8, 2012 - expectation value of the Higgs field 〈Φ〉 = v is the crucial quantity that gives mass to ... 2: Higgs potential in the complex plane of the Higgs field.
This is article 2 in the sequence entitled How the Higgs Field Works: with Math. Here is the previous article.
How does it happen that the Higgs field has a non-zero average value in nature, while the other (apparently-)elementary fields of nature that we know about so far do not? [Very fine point: other fields excepting the lowest-level gravitational field, called the “metric”, that helps establish the very existence of space and time.]
First, it is impossible for fermion fields to have a large constant non-zero average value in nature. This is related to the difference between fermions and bosons; bosons can be non-zero on average, but fermions really can’t. So we can forget about electrons (and their cousins the muons and the taus), about neutrinos, and about the quarks. [Fine point: Fermions can pair with each other or with anti-fermions to make composite bosons, and those composite bosons can be non-zero on average. In fact this is true of the up and down quarks and their antiquarks, and it is true of electrons in a superconductor. But that’s a long story, and not our immediate concern.]
What about the photon field, the gluon field, the W and the Z field? These are all bosons. In principle these fields could have a constant non-zero value on average throughout the universe. It is experiment, not theory, that says this isn’t the case. A large non-zero value for the electric field would have all sorts of effects that we do not observe, including most significantly an apparent violation of rotational invariance at large distance scales. The electric field is a vector (spin-1) — it points in a particular direction — so if it were non-zero, the direction in which its non-zero value points would be different from the other directions. See Figure 1, lower left.

Fig. 1: (Top) If no fields are non-zero on average, the vacuum of space has no preferred direction. (Bottom Left) If the electric field were non-zero on average, space would have a preferred direction — the direction in which the electric field points. No such preferred direction is observed in experiments. (Bottom Right) A non-zero value for the Higgs field does not change the fact that the vacuum has no preferred direction. Since the Higgs field is a relativistic field, it also does not change the fact that the vacuum has no preferred reference frame. In short, the effects of the non-zero Higgs field on the vacuum are minimal, and can only be inferred from changes in the properties of particles (in particular, their masses) in its presence.
The simplest way for the Higgs field to end up with a non-zero value throughout the universe would be if has a non-zero equilibrium value H0 that appears in its Class 1 equation of motion:
- d2H/dt2 – c2 d2H/dx2 = -(2 π νmin)2 (H – H0)
- d2H/dt2 – c2 d2H/dx2 = a2 H – b2 H3
- d2H/dt2 – c2 d2H/dx2 = – b2 H (H2 – [a/b]2)
- 0 = – b2 H (H2 – [a/b]2) (when H(x,t) is constant in x and t)
- H = 0
- H = + a/b
- H = – a/b
It isn’t instantly obvious, but the solution at H = 0 is unstable. The situation is analogous to the equation of motion for a ball in a bowl shaped like the one shown in Figure 2 — like the bottom of a wine bottle. This also has three equilibria, one at 0 and ones at ±x0. But clearly the equilibrium at 0 is unstable, in that even a tiny push will cause the red ball to roll far from x=0, a dramatic change. By contrast the equilibrium at x=x0 is stable, in that any little push will just cause the green ball to oscillate with small amplitude around the point x=x0, a not very dramatic change. (The same is true for the light green ball at x=-x0.) In a similar way, although H = 0 is a solution to the Higgs field’s equation, our universe’s history has been complex enough to assure that the Higgs field has been knocked around a bit, and so it can’t possibly be sitting there. Instead, the Higgs field ends up in a solution with a non-zero value, a situation which is stable.

Fig, 2: A ball in a bowl shaped like the bottom of a wine bottle can be in equilibrium either when placed in the well (green balls) or carefully balanced at the center of the bowl (red ball.) A small shake of the bottle will cause the red ball to fall off its balance point, but the green balls will remain almost where they were, merely oscillating a little around their equilibrium points. (Inset) By contrast a ball in a bowl with a simpler shape will have only one equilibrium, similar to a ball on a simple spring, and that equilibrium is stable against small shaking of the bowl. The Higgs field is non-zero because its equation of motion is like that of a ball at the bottom of a wine bottle.
- a = v b = (246 GeV) b
- d2H/dt2 – c2 d2H/dx2 = – b2 H (H2 – v2)
Now, although I’ve set things up so that H could be either v or -v, it doesn’t matter whether the value of the Higgs field is positive or negative (actually there are even more possibilities, see below); the world comes out looking the same, with the same physics, because nothing depends on the overall sign of H. This isn’t instantly obvious, but it’s true; one hint is that wherever you find H in the equations described in my overview of how the Higgs field works, it’s always H2 that appears, not H alone — and H2 doesn’t depend on whether H = v or H = -v. [Fine point: In fact, H is a complex field, with a real and an imaginary part, so H can be v times any complex number z with |z|=1; and in fact it’s always H*H = |H|2 that appears in the equations, which is independent of z. Even that’s not the whole story! but it’s good enough for today.]
If you find a way (perhaps using the proton-proton collisions at the Large Hadron Collider) to push or disturb the Higgs field a little bit somehow, it will wiggle back and forth — i.e., waves will develop, of the form
- H = v + A cos[2 π (ν t – x / λ)]
Higgs mechanism - Wikipedia, the free encyclopedia
en.wikipedia.org/wiki/Higgs_mechanism
Wikipedia
Loading...
Vacuum expectation value - Wikipedia, the free encyclopedia
en.wikipedia.org/wiki/Vacuum_expectation_value
Wikipedia
Loading...
[PDF]Lecture 17 - The Higgs Boson
www2.ph.ed.ac.uk/~playfer/PPlect17.pdf
University of Edinburgh
Loading...
[PDF]The Standard Model Higgs - High Energy Physics at The ...
hep.uchicago.edu/.../Lecture08%20Higgs.bw.pdf
University of Chicago
Loading...
2. Why the Higgs Field is Non-Zero on Average | Of ...
profmattstrassler.com/...higgs-field.../2-why-the-higgs-field-is-non-zero-...
[PDF]Physics of Higgs Bosons - UW High Energy Physics
www.hep.wisc.edu/~sheaff/.../Higgs.p...
University of Wisconsin‑Madison
Loading...

No comments:
Post a Comment