维基百科，自由的百科全书
热力学温度是温度的绝对测量量，是热力学的主要参数之一。
热力学温度由热力学第二定律定义，理论最低温度为零点。在称为绝对零度该点上，物质的粒子构成具有最小运动。在量子力学的描述中，绝对零度下的物质处于其基态，该状态下其能量最低。热力学温度因此也常被称为绝对温度。
国际单位制指定热力学温标为热力学温度的计量标度，并选择水的三相点273.16K作为基点。历史上一直在使用其他标准。使用华氏度作为单位间隔的朗肯温标，在美国的某些工程领域仍然用作英制工程单位的一部分。ITS-90给出了一个以非常高的精确度估计热力学温度的实用方法。 大体上，体静止时的温度是一种计量物质的粒子构成如分子，原子，亚原子粒子的平动、振动和转动的能量的方法。所有的这些运动的动能和粒子的势能，有时还包括某些其他类型的等效粒子能量构成物体的总内能。在物体不受外力或外力对其不做功的条件下，内能可以被不严格地称作热能。内能可以以多种方式存储于一种物质内，每种构成一个“自由度”。每个自由度有相同的能量平均值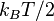
（
为玻尔兹曼常数），除非其处于量子体系。内部自由度（转动，振动等）适用于室温下的量子体系，平动自由度适用于经典体系，除了在极低的温度（开尔文的分数）下。大多数情况下，热力学温度由粒子的平均平动动能确定。
Thermodynamic temperature is the absolute measure of temperature and it is one of the principal parameters of thermodynamics.
Thermodynamic temperature is defined by the third law of thermodynamics in which the theoretically lowest temperature is the null or zero point. At this point, called absolute zero, the particle constituents of matter have minimal motion and can become no colder.[1][2] In the quantum-mechanical description, matter at absolute zero is in its ground state, which is its state of lowest energy. Thermodynamic temperature is often also called absolute temperature, for two reasons: one, proposed by Kelvin, that it does not depend on the properties of a particular material; two that it refers to an absolute zero according to the properties of the ideal gas
Roughly, the temperature of a body at rest is a measure of the mean of the energy of the translational, vibrational and rotational motions of matter's particle constituents, such as molecules, atoms, and subatomic particles. The full variety of these kinetic motions, along with potential energies of particles, and also occasionally certain other types of particle energy in equilibrium with these, make up the total internal energy of a substance. Internal energy is loosely called the heat energy or thermal energy in conditions when no work is done upon the substance by its surroundings, or by the substance upon the surroundings. Internal energy may be stored in a number of ways within a substance, each way constituting a "degree of freedom". At equilibrium, each degree of freedom will have on average the same energy: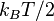 where is the Boltzmann constant, unless that degree of freedom is in the quantum regime. The internal degrees of freedom (rotation, vibration, etc.) may be in the quantum regime at room temperature, but the translational degrees of freedom will be in the classical regime except at extremely low temperatures (fractions of kelvins) and it may be said that, for most situations, the thermodynamic temperature is specified by the average translational kinetic energy of the particles.
一代天骄波尔兹曼（Boltzmann）与统计物理（3）
热力学温度由热力学第二定律定义，理论最低温度为零点。在称为绝对零度该点上，物质的粒子构成具有最小运动。在量子力学的描述中，绝对零度下的物质处于其基态，该状态下其能量最低。热力学温度因此也常被称为绝对温度。
国际单位制指定热力学温标为热力学温度的计量标度，并选择水的三相点273.16K作为基点。历史上一直在使用其他标准。使用华氏度作为单位间隔的朗肯温标，在美国的某些工程领域仍然用作英制工程单位的一部分。ITS-90给出了一个以非常高的精确度估计热力学温度的实用方法。 大体上，体静止时的温度是一种计量物质的粒子构成如分子，原子，亚原子粒子的平动、振动和转动的能量的方法。所有的这些运动的动能和粒子的势能，有时还包括某些其他类型的等效粒子能量构成物体的总内能。在物体不受外力或外力对其不做功的条件下，内能可以被不严格地称作热能。内能可以以多种方式存储于一种物质内，每种构成一个“自由度”。每个自由度有相同的能量平均值
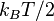（为玻尔兹曼常数），除非其处于量子体系。内部自由度（转动，振动等）适用于室温下的量子体系，平动自由度适用于经典体系，除了在极低的温度（开尔文的分数）下。大多数情况下，热力学温度由粒子的平均平动动能确定。Thermodynamic temperature is the absolute measure of temperature and it is one of the principal parameters of thermodynamics.
Thermodynamic temperature is defined by the third law of thermodynamics in which the theoretically lowest temperature is the null or zero point. At this point, called absolute zero, the particle constituents of matter have minimal motion and can become no colder.[1][2] In the quantum-mechanical description, matter at absolute zero is in its ground state, which is its state of lowest energy. Thermodynamic temperature is often also called absolute temperature, for two reasons: one, proposed by Kelvin, that it does not depend on the properties of a particular material; two that it refers to an absolute zero according to the properties of the ideal gas
Roughly, the temperature of a body at rest is a measure of the mean of the energy of the translational, vibrational and rotational motions of matter's particle constituents, such as molecules, atoms, and subatomic particles. The full variety of these kinetic motions, along with potential energies of particles, and also occasionally certain other types of particle energy in equilibrium with these, make up the total internal energy of a substance. Internal energy is loosely called the heat energy or thermal energy in conditions when no work is done upon the substance by its surroundings, or by the substance upon the surroundings. Internal energy may be stored in a number of ways within a substance, each way constituting a "degree of freedom". At equilibrium, each degree of freedom will have on average the same energy:
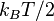where is the Boltzmann constant, unless that degree of freedom is in the quantum regime. The internal degrees of freedom (rotation, vibration, etc.) may be in the quantum regime at room temperature, but the translational degrees of freedom will be in the classical regime except at extremely low temperatures (fractions of kelvins) and it may be said that, for most situations, the thermodynamic temperature is specified by the average translational kinetic energy of the particles.一代天骄波尔兹曼（Boltzmann）与统计物理（3）
|||
上两篇博文絮絮叨叨谈了第二定律发现过程的前三步。下面要说第四步。本来呢，按不才的风格，一页纸把四大步都说尽，岂不痛快。不料又有红颜知己说你历来心高气傲，说什么事不点到即止，一副“那还用说？”的臭架子。那就啰嗦一点吧。其实这四步推演，都可分别在不同的地方或书中找到。本人将其制成羊肉串，不仅仅为了吃着香，是让人别忘了第二定律多么简单明了，而其妊娠诞生多么艰难，给工业界带来多少福祉，给科学界带来多少美梦与噩魇，那一个名词“熵”，便把物理界搞得神魂颠倒，天下大乱，群雄遍野。几世几劫过去，至今仍不见大治。君不见There are as many viewpoints as physicists in statistical mechanics.忘了谁说的。
话说十九世纪中叶，力学及热力学界国际基本格局是德英法鼎足而立。应该是当年莱布尼兹、牛顿和笛卡尔三个王者英姿勃发三分力学天下的遗产。君不见这阵容，南有法兰西卡诺、科拉贝红（Clapeyron）、及后来的彭佳来（Poincaré）等，西有英伦哈密屯（Hamilton）、汤姆孙、焦耳及后来的麦克斯韦（Maxwell）等，北有日耳曼克劳修斯（Clausius）、赫兹（Hertz）、海姆火滋（Helmholtz）及后来的波尔兹曼等。
单说这克劳修斯，格物之功了得，对着天使热机，务要即物穷理，十几年如一日。熬到1865年，成了正果，终于把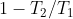
背后的‘理’穷尽，大白于天下。说来令人吃醋而嘡目，没什么神秘的，不过脑筋急转弯，半分钟推算完毕。设
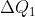为高温热源给热机的热量，
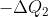为低温热源给热机的热量。那么根据定义，热机转一圈回到原地，效率就是
。
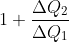如果是卡诺可逆热机，如汤姆孙所说，此效率必等于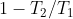。立马写出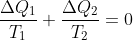
。这个公式可写成热机转一圈吸收N次热量，每个热量被当时的温度除，都加起来等于零。意思是可逆热机有个重要的函数，他命名为熵(entropy)S。其变化就是
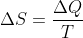。转一圈变化为零说明它是位置（状态）函数，跟路径无关。这位乱世奸雄就此诞生。且慢，这只是第二定律的一个面目。
如果是不可逆热机，此效率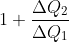必小于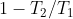（小卡诺说的），立刻写出
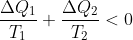。与可逆热机的熵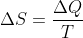及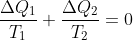比较一下， 立刻可以写出
。
这就是克劳修斯完成的第四步，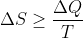
也称为克劳修斯不等式，即后来的热力学第二定律。本人生在当时就好了。
诸位读过这三篇博文，不知有何感想。我的一个感想是，其理、其逻辑、其推演如此简单明了，想违反它是不可能的。除非永动机再世。如果你自己定义一个“熵”，如上文的三个例子，那是另一回事，与克劳修斯的熵沾不上亲戚。没必要用热力学第二定律的英名做广告。
但这些博文的目的不在于第二定律本身。而是说说波尔兹曼大闹天宫的历史背景。当时及后来对熵的理解是，它代表运动状态的混乱程度。物质是由小粒子构成的力学系统。那这力学运动的混乱度为什么只升不落（对孤立体系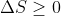
）？二十几岁的波尔兹曼，初生牛犊，就有一个梦想：第二定律是力学体系的行为，只能用牛顿力学解释。哪成想，这一下捅了天大的娄子。。。
话说十九世纪中叶，力学及热力学界国际基本格局是德英法鼎足而立。应该是当年莱布尼兹、牛顿和笛卡尔三个王者英姿勃发三分力学天下的遗产。君不见这阵容，南有法兰西卡诺、科拉贝红（Clapeyron）、及后来的彭佳来（Poincaré）等，西有英伦哈密屯（Hamilton）、汤姆孙、焦耳及后来的麦克斯韦（Maxwell）等，北有日耳曼克劳修斯（Clausius）、赫兹（Hertz）、海姆火滋（Helmholtz）及后来的波尔兹曼等。
单说这克劳修斯，格物之功了得，对着天使热机，务要即物穷理，十几年如一日。熬到1865年，成了正果，终于把
如果是卡诺可逆热机，如汤姆孙所说，此效率必等于
如果是不可逆热机，此效率
这就是克劳修斯完成的第四步，
诸位读过这三篇博文，不知有何感想。我的一个感想是，其理、其逻辑、其推演如此简单明了，想违反它是不可能的。除非永动机再世。如果你自己定义一个“熵”，如上文的三个例子，那是另一回事，与克劳修斯的熵沾不上亲戚。没必要用热力学第二定律的英名做广告。
但这些博文的目的不在于第二定律本身。而是说说波尔兹曼大闹天宫的历史背景。当时及后来对熵的理解是，它代表运动状态的混乱程度。物质是由小粒子构成的力学系统。那这力学运动的混乱度为什么只升不落（对孤立体系
No comments:
Post a Comment